基于声散射模型的鱼雷自噪声特性分析及仿真预报

徐园园, 王明洲, 蒋继军, 李斌



基于声散射模型的鱼雷自噪声特性分析及仿真预报

徐园园1, 2, 王明洲1, 2, 蒋继军1, 2, 李斌1

(1. 中国船舶重工集团公司 第705研究所, 陕西 西安, 710075; 2. 水下信息与控制重点实验室, 陕西 西安, 710075)

针对水下高速航行时鱼雷的主要自噪声源——螺旋桨噪声, 分析了其通过散射传播形成的自噪声, 以水下声散射理论为依据, 在忽略雷长情况下建立了简化的自噪声场物理模型, 计算了自噪声平均强度级, 分析了鱼雷辐射噪声级(螺旋桨噪声形成的辐射噪声)、声吸收系数、散射系数、航深等参数对自噪声的影响。仿真结果表明, 变化规律与经验数据吻合, 证明了该模型的正确性和有效性。

鱼雷; 自噪声; 声学散射; 自噪声仿真预报

0 引言

对于自导鱼雷, 其信号处理的性能与声纳基阵接收数据的信噪比有关, 即随着信噪比的下降而降低。因此, 自噪声的预报与研究对鱼雷的声自导作用距离、探测精度等有着重要作用。

鱼雷自噪声的来源主要有机械噪声、螺旋桨噪声及流噪声。其中, 在低速、海况级别高的情况下, 机械噪声占主要地位。在中速时, 流噪声是主导噪声[1]。航速超过20 kn的情况下, 虽然流噪声随航速的增大而增加, 但螺旋桨噪声开始占主导地位。且在千赫兹频段上螺旋桨空化噪声将是主要噪声源[2]。本文研究了高频段、高航速条件下螺旋桨噪声通过声散射形成的鱼雷航行自噪声强度。

1 水下噪声声散射原理

鱼雷自噪声源所产生的声和振动, 通过不同的路径到达鱼雷头部声纳。

图1为螺旋桨噪声通过海水传播到达鱼雷头部声纳的路径。图中, 通过路径海洋中的散射体反向散射螺旋桨噪声, 引起体积散射自噪声,为通过海面散射螺旋桨噪声的路径,为海底散射路径。

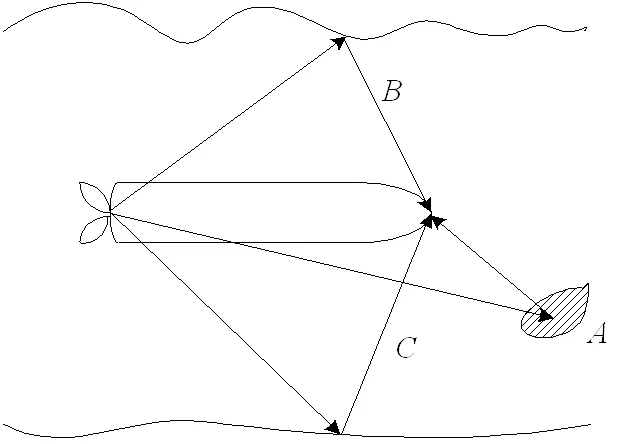
图1 螺旋桨噪声的传播路径

螺旋桨噪声通过,,这3种声散射路径传播到鱼雷头部声纳而形成的自噪声即为鱼雷散射自噪声, 这是鱼雷自噪声的一个重要组成部分。通过体积散射体反向散射的螺旋桨噪声称为体积散射自噪声; 通过分布在界面上的散射体散射所形成的自噪声称为界面散射自噪声。最显著的散射界面是海面和海底。

不同于文献[3]~[7], 本文依据文献[2]中混响散射模型的基本理论, 推导鱼雷散射自噪声。但在混响散射模型中杂波噪声为窄带脉冲, 时间域上只在脉宽内有信号, 而自噪声在时间域上连续, 任意时刻都存在噪声信号, 直接导致了散射体元选法的差异。

假设鱼雷自导为无指向性单个换能器, 换能器与螺旋桨噪声源的距离为(雷长), 当散射路径足够长时,的影响可以忽略, 因此将鱼雷头部声纳视为收发同置换能器。

2 鱼雷散射自噪声模型

2.1 体积散射自噪声理论模型

图2 体积散射模型坐标系

图3 体积散射体元

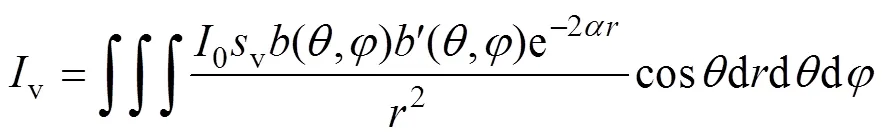
体积散射自噪声预报中, 通过积分计算得换能器接收体积散射自噪声

体积散射自噪声级

2.2 界面散射自噪声理论模型

1) 通过散射界面所散射的螺旋桨噪声信号在同一时刻返回鱼雷头部声纳才能进行叠加。

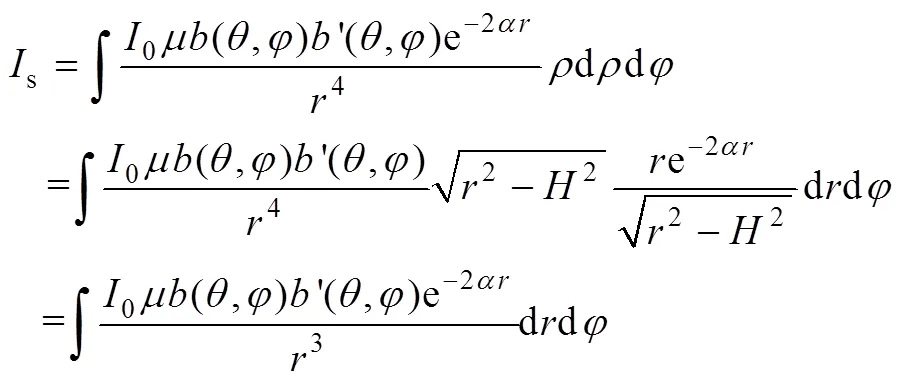
界面散射自噪声预报中, 粗糙表面对声的散射满足Lambert定律[1]。即界面散射系数

(9)

界面散射自噪声级

3 仿真分析

3.1 鱼雷自噪声仿真预报

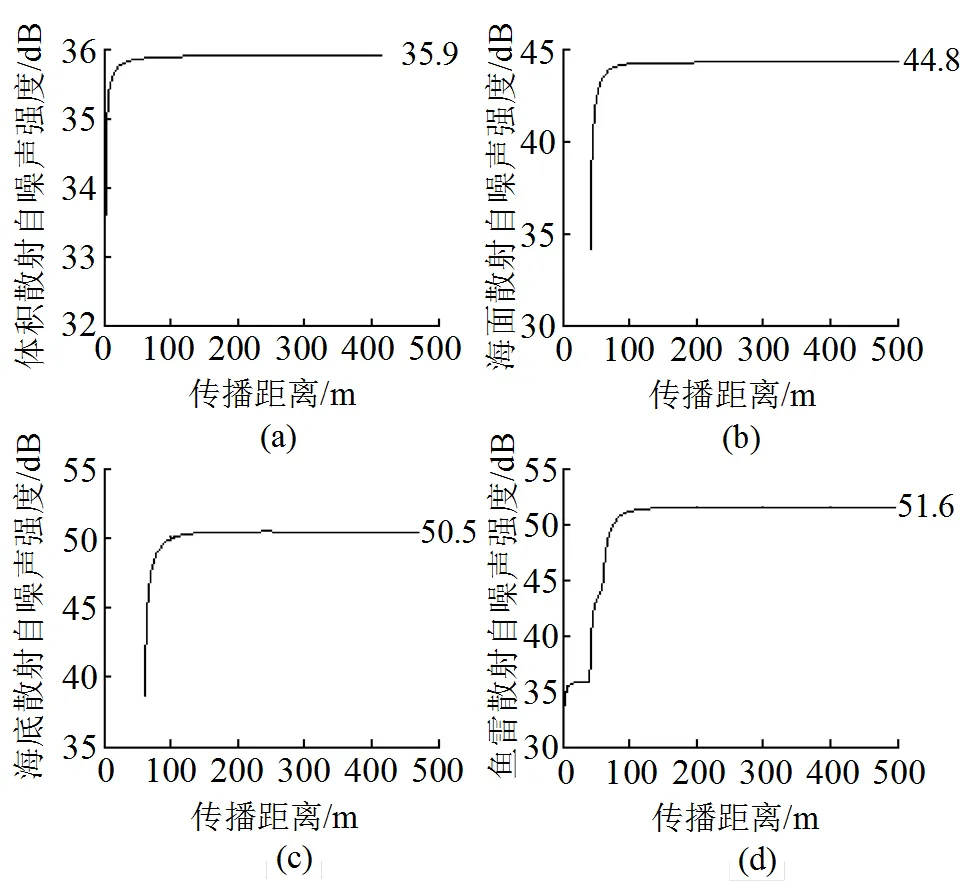
图5 散射自噪声强度随传播距离的变化规律

3.2 鱼雷散射自噪声随参数的变化规律

改变鱼雷螺旋桨辐射噪声级、散射系数、声吸收系数以及航行深度等参数, 进行计算机仿真, 研究体积散射、界面散射及鱼雷散射自噪声强度随参数变化的规律。

3.2.1 散射自噪声随螺旋桨噪声的变化关系

仅改变辐射噪声级, 不同航速下辐射噪声谱级与散射自噪声级的关系如表1所示。

表1 散射自噪声随螺旋桨辐射噪声级的变化规律

鱼雷的辐射噪声与航速有直接关系[4]。由表1可看出, 随着航速的增加, 鱼雷辐射噪声增加, 鱼雷散射自噪声也相应增加, 且鱼雷散射自噪声与辐射噪声成正比关系。

3.2.2 散射自噪声随声吸收系数的变化规律

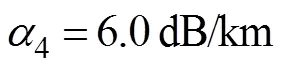
图6中, (a), (b), (b), (d)分别为体积散射、海面散射、海底散射及鱼雷散射自噪声随声吸收系数的变化关系曲线。由于温度、盐度不同, 海水声吸收系数不同, 散射体积自噪声随声吸收系数的增大而减小。这是因为声吸收系数越大, 噪声信号在海水中的衰减越大。

图6 散射自噪声强度随声吸收系数的变化规律

3.2.3 散射自噪声随散射系数的变化规律

在仅改变散射系数条件下, 研究散射自噪声与散射系数的关系[2]。

图7 体积散射自噪声随体积散射系数的变化关系

2) 界面散射系数。仅改变海面或海底散射系数, 在上述条件下进行仿真, 结果分别见表2和表3。由表中数据可知, 界面散射系数越大, 散射体散射能力越强, 界面散射自噪声级越大, 且其与散射系数成正比关系。

表2 海面散射自噪声随散射系数的变化规律

表3 海底散射自噪声随散射系数的变化规律

3.2.4 散射自噪声随航行深度的变化规律

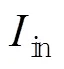
图8 体积散射自噪声随航行深度的变化关系

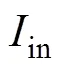
4 结束语

本文基于声散射模型对鱼雷自噪声进行了建模, 推导出体积散射、界面散射及鱼雷散射自噪声预报公式, 仿真讨论了鱼雷自噪声随不同参数的变化规律。仿真结果表明, 该理论模型得出的鱼雷自噪声级与文献中自噪声级的强度测量值范围[3]、规律一致, 证明了该理论模型的有效性, 对高频、高航速下鱼雷自噪声的预报有实际意义。

[1] Wsite A D. 实用声纳工程[M]. 王德石, 译. 北京: 电子工业出版社, 2004: 79-111.

[2] R. J. 尤立克. 水声原理[M]. 洪申, 译. 哈尔滨: 哈尔滨船舶工程学院出版社, 1990: 190-240.

[3] 李国付. 鱼雷自导作用距离估算方法[D]. 西安: 西北工业大学, 2007: 16-30.

[4] 王国治, 童宗鹏. 鱼雷动力机械水下噪声预报研究[J]. 鱼雷技术, 2002, 10 (4): 18-21.Wang Guo-zhi, Tong Zong-peng.Research in the Prediction of Underwater Noise Caused by the Power Machinery in Torpedo[J]. Torpedo Technology, 2002, 10(4): 18-21.

[5] 杜向党, 秦丽萍, 石秀华. 鱼雷头部自噪声计算方法[J]. 弹箭与制导学报, 2006, 26( 3): 140-145. Du Xiang-dang, Qin Li-ping, Shi Xiu-hua. Computing Method for the Self-noise of Torpedo[J]. Journal of Projectiles, Missiles and Guidance, 2006, 26( 3): 140-145.

[6] 陈春玉, 易红, 郝保安, 等. 鱼雷发电机噪声对自导系统的干扰及其抗干扰技术[J]. 鱼雷技术, 2007, 15(6): 17-19.Chen Chun-yu, Yi Hong, Hao Bao-an, et al. Influence of Noise from Torpedo Electric Generator on Homing System and Counterm Easures[J]. Torpedo Technology, 2007, 15(6): 17-19.

[7] 赵加鹏, 石秀华, 杜向党. 鱼雷流噪声的综合预报方法研究[J]. 鱼雷技术, 2009, 17(2): 10-14. Zhao Jia-peng, Shi Xiu-hua, Du Xiang-dang. An Integrated Prediction Method of Torpedo Flow Noise[J]. Torpedo Technology, 2009, 17(2): 10-14.

[8] Eberhard Z, Wolfgang H, Schwarz H. 数学指南[M]. 北京: 科学出版社, 2012: 138-210.

Characteristic Analysis and Prediction Simulation of Torpedo Self-Noise Based on Acoustic Scattering Model

XU Yuan-yuan1,2, WANG Ming-zhou1,2, JIANG Ji-jun1,2, LI Bin1

(1. The 705 Research Institution, China Shipbuilding Industry Corporation, Xi′an 710075, China; 2. Science and Technology on Underwater Information and Control Laboratory, Xi′an 710075, China)

Propeller noise forms the main self-noise source of a torpedo running at high speed under water by scattering propagation. According to the underwater acoustic scattering theory, a simplified self-noise field physical model is constructed by ignoring torpedo length to calculate the average intensity level of self-noise and analyze the influences of the parameters, such as the radiated noise level from torpedo propeller, the sound absorption coefficient, the scattering coefficient, and the running depth, on the self-noise. Simulation results coincide with the empirical data, indicating the validity and effectiveness of this model.

torpedo; self-noise; acoustic scattering; prediction simulation of self-noise

TJ630.1; TB56

A

1673-1948(2013)02-0105-05

2012-07-19;

2012-08-27.

徐园园(1988-), 女, 在读硕士, 研究方向为水声工程.

(责任编辑: 杨力军)