基于各向异性分形几何理论的摩擦非线性数学模型
2013-05-24田红亮赵春华方子帆朱大林秦红玲刘芙蓉钟先友
田红亮,赵春华,方子帆,朱大林,秦红玲,刘芙蓉,钟先友
将式(21)、(42)、(29)代入式(45)得:
摩擦是研究相互作用表面及其有关理论与实践的科学,涉及物理、化学及材料等学科,摩擦的应用覆盖机械、材料、化工、石油及冶金等领域。我国的空间固体润滑材料、微机械制造摩擦学、纳米颗粒润滑材料与技术等成果已应用于我国空间技术领域,解决了航天、航空和船舶等领域多项润滑技术难题。摩擦是一种复杂的、非线性的、具有不确定性的自然现象,人类目前对于摩擦的物理过程的了解还只停留在定性认识阶段,无法通过数学方法对摩擦过程给出精确描述[1-2],所以准确预测静摩擦特性会变得困难。传统的Coulomb摩擦第1定律认为:摩擦力与接触面所承受的法向载荷成正比例,静摩擦系数与法向载荷无关,也不决定于接触面所承受的切向载荷,只随接触材料的变化而不同。但随着近代摩擦学的发展,发现①Coulomb摩擦第1定律中摩擦力与法向载荷不成正比例,而呈现出非线性关系,这是因为法向载荷对摩擦系数的影响与材料之间的真实接触面积有关,根据粘着理论,只有当材料之间真实接触面积与法向载荷成正比时,材料摩擦系数才与法向载荷无关,这种情况只发生在微突起主要成塑性变形或微突起成弹性变形,而其高度成指数分布的状态,在一般状态下,微突起处于弹塑性变形状态,故摩擦系数将与法向载荷有关[3];②静摩擦系数对于同种材料不变的结论不能很好地反映工程实践;③在一定条件下,静摩擦系数随着法向载荷的变大而变大。
自1508年达芬奇开始把摩擦学引入理论研究的途径以来,诸多学者一直开展摩擦特性的工作。Chang等[4]依照经典的Greenwood-Williamson综合弹性接触理论[5],涉及粘着力的作用,架构金属粗糙表面间的静摩擦系数计算模型。尤晋闽等[6]综合探究微突起的完全弹性、弹-塑性及完全塑性等不同变形机制,构建干摩擦的静摩擦系数的统计计算模型,该模型考虑完全弹性区、弹-塑性Ⅰ区的接触点承担切向载荷的水平,得到“静摩擦系数随着法向载荷的增大而减小”的结论,支持古典摩擦结论[7-9]。表面粗糙度对摩擦系数有较大影响[10],盛选禹等[11]沿袭 Majumdar-Bhushan 弹塑性接触分形模型[12],综合考虑分形维数D、分形粗糙度G、材料性能参数φ、相关因子K的作用,预测静摩擦系数的变化规律。但文献[12]在推导微突起曲率半径R时存在1个计算原理性瑕疵[13]。另外,文献[11]在计算方法上具有一些不足之处:①法向总载荷、总摩擦力皆应该是有条件等式[14],这是因为接触面在法向载荷作用下,处于塑性变形的微突起由于受到局部接触载荷作用而发生塑性流动,将不能继续承受切向载荷,因此在计算静摩擦力时只包含完全弹性区的微突起;②按文献[12]的计算方法,引起一些公式错误;③给出“f随φ的增加而降低”的观点与实际相反;④静摩擦系数的数字仿真数据在0.001~1 000之间,与工程实际表面静摩擦系数的分布区间0~1相隔较远;⑤假定粗糙表面的微观形貌各向同性。
鉴于以上原因,本文应用各向异性分形几何理论,探索金属接触面最大静摩擦力的来源机理,构建法向载荷、最大静摩擦力、静摩擦系数的非线性数学模型,使用数值模拟,预测摩擦特性,本文分析结果与经典摩擦学论点有偏离,探讨导致这些偏离的原因。
1 各向异性分形几何理论
配对摩擦副实质上是由两个粗糙表面组成的,在微观状态下可以形象化地把两个粗糙表面的接触看作是一系列微突起的接触,当表面受到挤压,微突起将发生弹性或者塑性变形。
1.1 弹性接触时一个微突起的实际微接触面积
由于粗糙表面轮廓对工程研究可认为是连续的,而且随着放大倍数的增加,在任何一点上都会呈现出更多的具有统计自相似自仿射性的粗糙度细节。Ausloos-Berman函数能模拟一个各向异性分形表面轮廓的几何形貌,该函数[15]为:
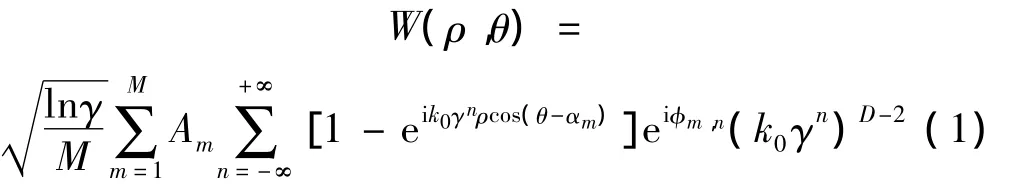

表面轮廓的高度能用式(1)的实部导出:
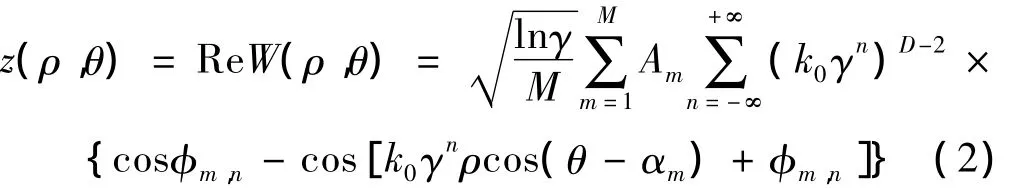
将式(1)中的一些注释代入式(2)得:
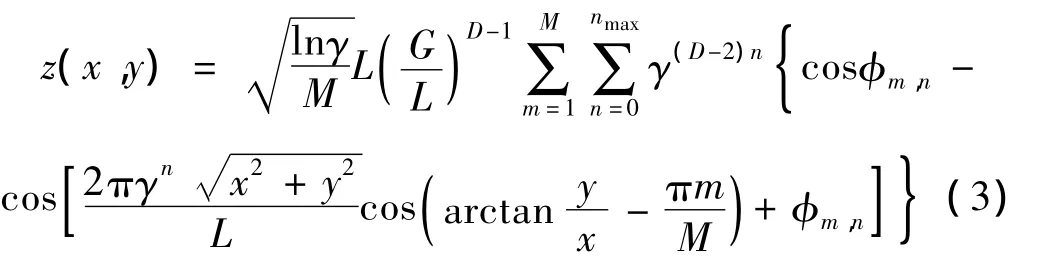
式中nmax为与测量长度Ls相关的指数,且:
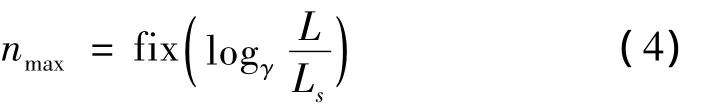
这里fix为向零方向取整。
若 M =10、γ =1.5、L=0.4 μm、G=1.36 ×10-5μm时,式(3)仿真不同分形维数的各向异性表面轮廓高度见图1。从图1中可以看出,在x→0,y→0附近,表面轮廓高度急剧降低,故式(3)可仿真在微观上有缺陷的接触面,即向材料内凹陷的裂纹、点蚀坑,例如灰铸铁的组织结构就如同在钢的基体上嵌入大量石墨片,石墨的存在相当于在基体上分布大量孔洞,特别是片状石墨的尖角引起应力集中;当x→0,y→0时,表面轮廓高度很低,几乎趋于零,事实上,按照式(3)易得二元函数的极限
若M=1,则m=1时,式(3)退变为:
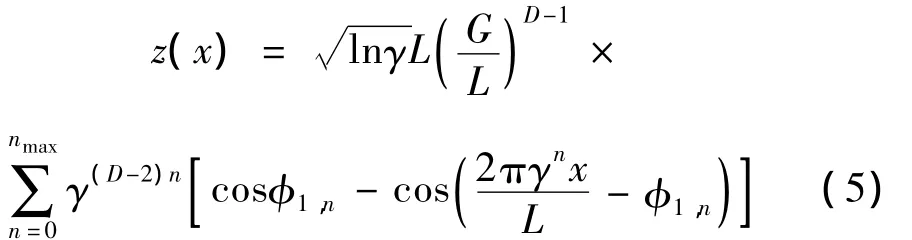
有趣的是,式(5)与y无关。
设横截微接触点的半径为r',微突起波形式的最长波长为2r',取Ls=2r'。按式(4)可得基波长微突起对应的频率指数满足:

上式在式(5)中对应的一项为:
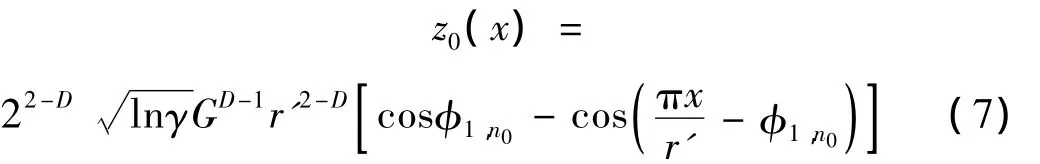
选择合适的两自变量φ1,n0,x使z0(x)最大。如将φ1,n0=0,x=r'代入式(7),可得微突起变形量为:
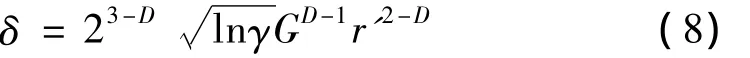
当表面受到挤压时,一个球体状微突起将发生弹性变形见图2,其中Pe为一个微突起承担的法向弹性载荷;R为一个微突起顶端的曲率半径;r为弹性接触时一个微突起实际微接触面积的半径;E'为两接触物体的综合弹性模量。

图1 不同分形维数的表面轮廓高度Fig.1 Surface profile height with different fractal dimensions
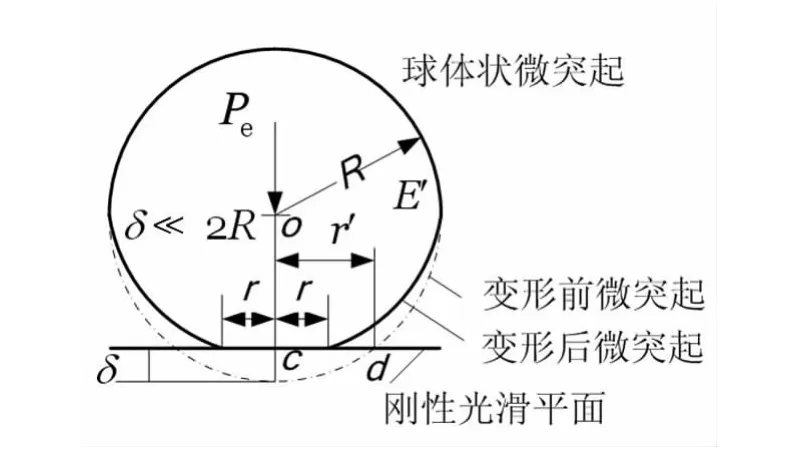
图2 球体状微突起与刚性光滑平面的弹性接触Fig.2 Elastic contact of spherical asperity and rigid smooth surface
对图2的直角三角形ocd使用勾股定理得:
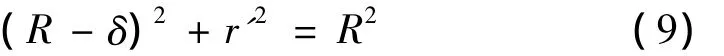
化简上式得:


将式(8)代入式(11)得:

进一步可写为:
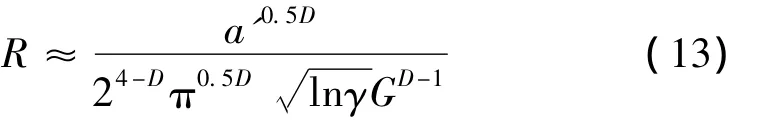
这里a'为一个微突起的横截微接触面积,a'=πr'2。
弹性接触时一个微突起实际微接触面积的半径[19]为:
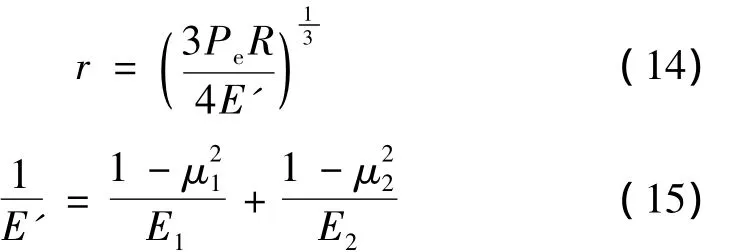
式中:E1、E2分别为两个接触物体的弹性模量;μ1、μ2分别为两个接触物体的泊松比。
值得指出的是,式(15)与文献[19]的式(2-13)不同。
一个微突起承担的法向弹性载荷[4]为:
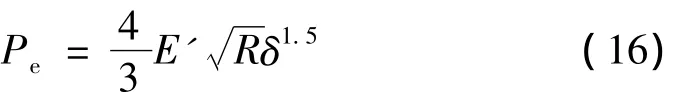
将式(16)代入式(14)得:

将式(11)代入式(17)得:

将式(18)代入式(14)得:

接着式(19)可变形为:
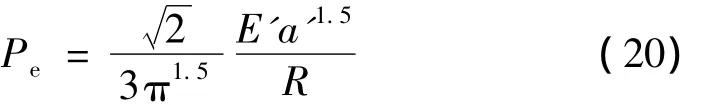
将式(13)代入式(20)得:

由式(13)的注释、式(18)可得弹性接触时一个微突起的实际微接触面积为:

1.2 完全塑性接触时一个微突起的实际微接触面积
一个微突起承担的法向塑性载荷[12]为:

式中:K为相关因子;σy为较软材料的屈服强度。
一个塑性变形微突起的实际微接触面积[4]为:

这里δc为一个微突起的临界变形量。
当2δ≫δc时,完全塑性接触时一个微突起的实际微接触面积为:

运用式(13)的注释、式(18)得:

将式(17)代入式(26)得:

使用式(25)暨(27),可得完全塑性接触时一个微突起的实际微接触面积为:

将式(28)代入式(23)得:

1.3 接触面承担的法向总载荷
一个微突起的临界变形量[4]为:

这里b为待求解的无量纲正常数。
将式(13)代入式(30)得:

式(8)可改写为:
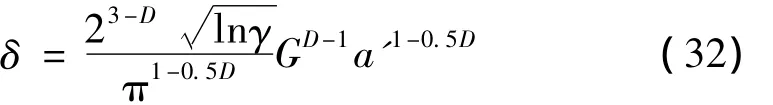
式(32)除以式(31)得:
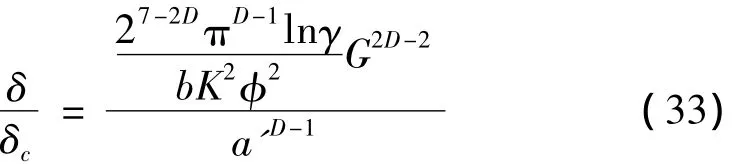
当δ=δc时,可得惟一解a',即为划分弹塑性区域的临界微接触截面积:
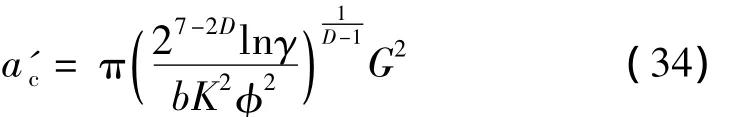
将式(34)代入式(33)得:

由于 1≤D≤2,则 a'≥a'c时,可得 δ≤δc,接触微突起发生弹性变形;而则a'<a'c时,可得δ>δc,接触微突起发生塑性变形。
考虑式(21)与(29),划分弹塑性区域的临界微接触截面积a'c匹配的一个微突起承担的法向弹性载荷、法向塑性载荷分别为:
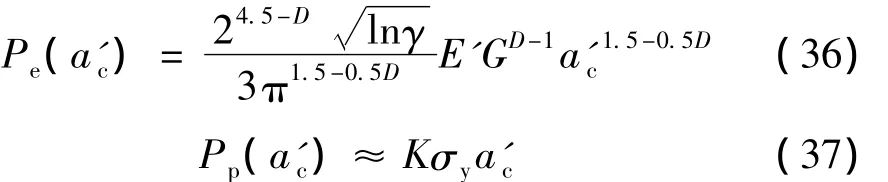
两接触粗糙表面在逐渐变大的法向总载荷作用下,并列分布的一系列微突起承担法向载荷。如果一个微突起承担的法向载荷函数在点划分弹塑性区域的临界微接触截面积ac'连续,即 Pe(ac')=Pp(ac'),或:
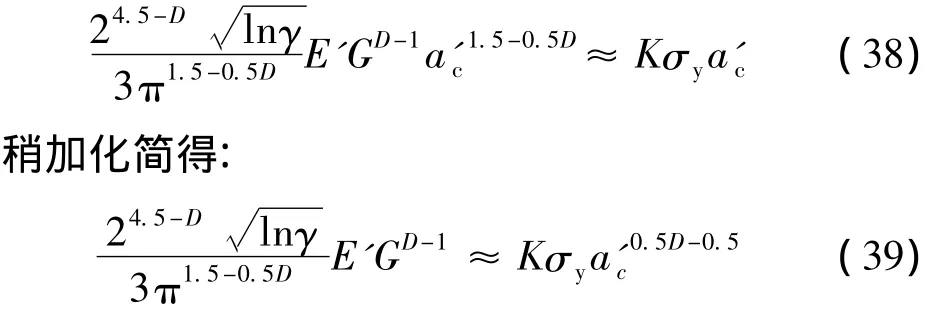
将式(34)代入式(39)得:

需要说明的是式(40)不同于文献[15]。
将式(40)代入式(34)得:
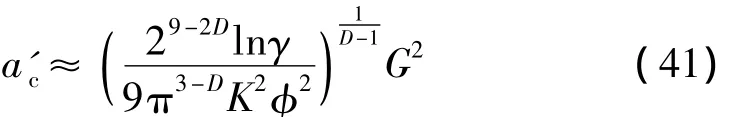
微突起微接触截面积的大小分布函数[20]为:n(a')=0.5Dψ1-0.5Da'L0.5Da'-1-0.5D,0 < a'≤ a'L(42)这里ψ为域扩展因子。
整个接触面的实际接触面积为:
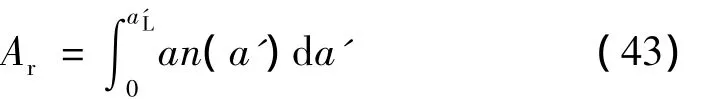
需要强调式(43)异于文献[15]的式(8)。
将式(22)、(42)代入式(43)得:
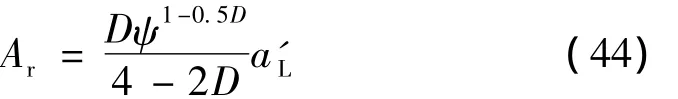
整个接触面承受的法向总载荷为:
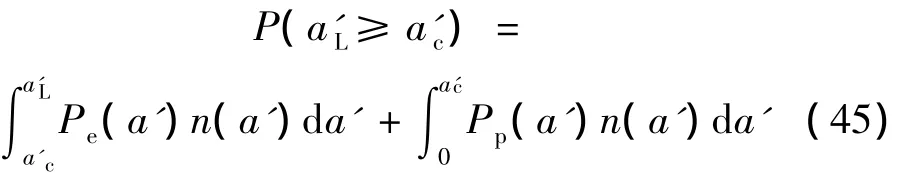
将式(21)、(42)、(29)代入式(45)得:
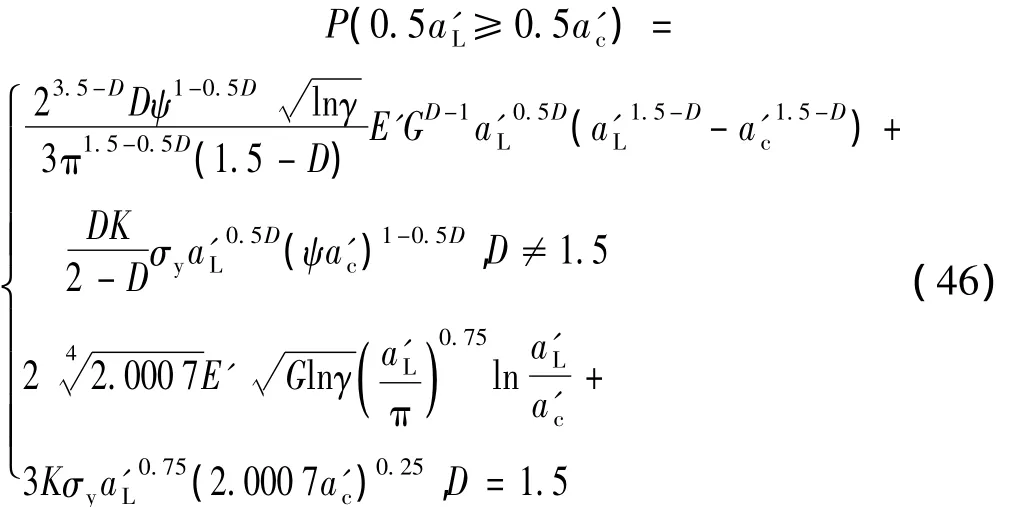
值得指出式(46)异于文献[15]的式(13)、(16)。
仿照式(22)得:

将式(47)代入式(44)得:
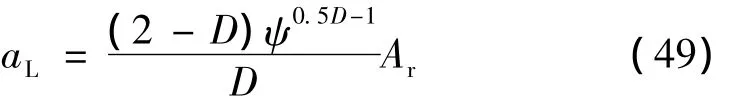
将式(47)、(48)代入式(46)得:
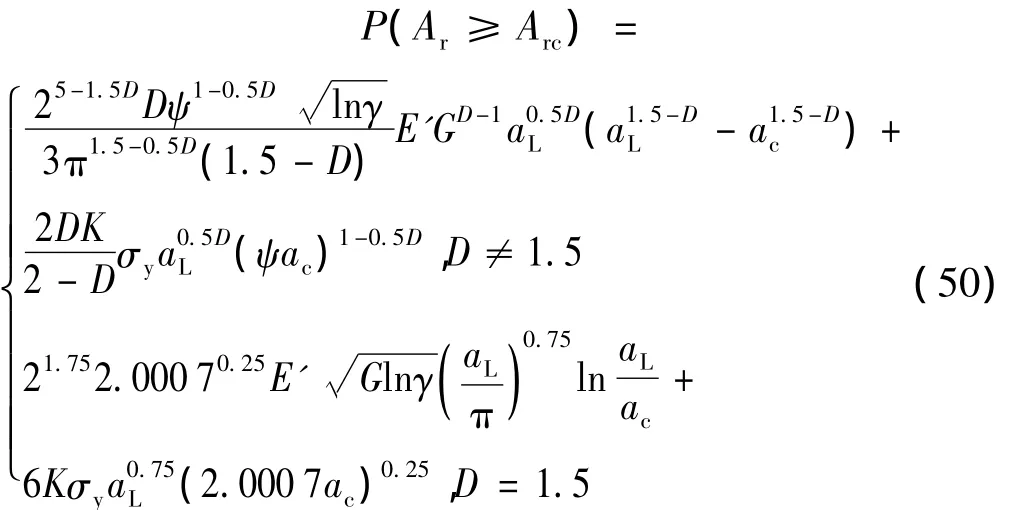
这里Arc为实际临界接触面积,且:
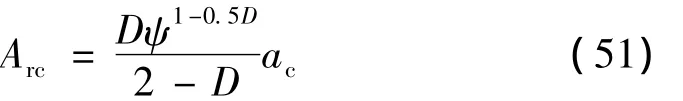
依靠式(49)得:

式中:Aa为整个接触面的宏观接触面积为整个接触面的接触率。
将式(52)代入式(50)得:

2 接触面的最大静摩擦力与静摩擦系数
对整个接触面承受法向载荷和切向力,应力场目前还没有完整的解析解。现有的有关文献都根据一定的假设进行了简化。田红亮等[21]指出,如果两个力T(一个微突起承担的切向力)、Pe(一个微突起承担的法向弹性载荷)的比例小于0.3,屈服将发生在表层以下,如果比例大于0.3,屈服将发生在接触点的边缘。为使应力表达式简化,假设屈服将发生在接触点的边缘。此时接触点边缘的接触面三个主应力分别为:
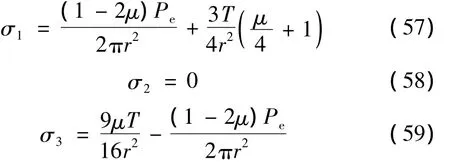
这里μ为较软材料的泊松比。
需要说明式(57)不同于文献[6]的式(2)。
解释屈服失效的第3强度理论[22]为:

将式(57)、(59)代入式(60)中,有:
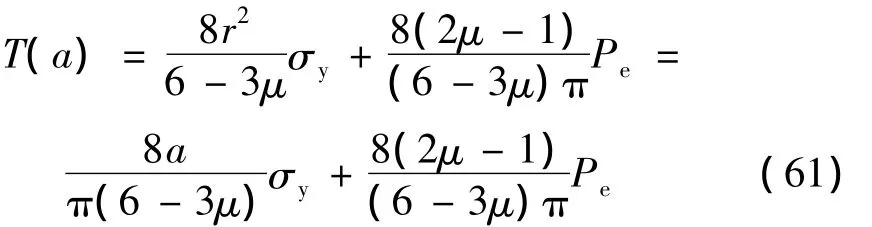
将式(22)代入式(61)得:
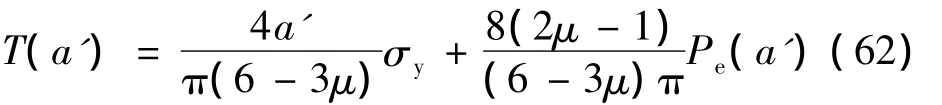
假设已经发生塑性变形的微突起,由于局部的接触载荷已经使其发生塑性流动,将不能继续承受切向载荷,因此在计算最大静摩擦力时不包括已经发生塑性变形的微突起。没有达到弹性极限的微突起能够继续承受切向载荷,对最大静摩擦力有贡献。当切向力逐渐增大时,只有弹性变形的微突起最终将达到屈服,此时的切向力就是最大静摩擦力。所以最大静摩擦力为:
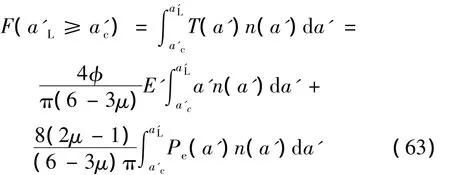
将式(42)、(21)代入式(63)中,有:

需要说明式(67)不同于文献[15]的式(25)。
下面将对本文所提出的理论公式进行数字仿真。在接下来的仿真研究中,先假设某个分形参数确定,然后让另外一个或二个分形参数变化,研究静摩擦非线性特征的变化规律,但分形参数他们之间不是相互独立的,各参数需满足不等式献[12],近似选择接触率的上限为0.1,即0.1≥A*r,故适合不等式划分分形维数D、域扩展因子ψ、相关因子K、材料性能参数φ、表面轮廓频谱密度相关的参数γ、无量纲分形粗糙度G*有效范围的依据,且0.5≤K≤3。因此后续的6个仿真参数 D、ψ、K、φ、γ、G*的选择绝不是简单意义上的纯数学游戏,否则不考虑不等式,就会出现文献[23]中的3个弊端(图3、4、6的纵坐标接触率A*r在0刻度以下都有坐标)。
3 法向总载荷对实际接触面积的影响
在理论上如何精确计算整个接触面的接触率A*
r,是传统摩擦学的一个悬而未决难点。依据式(53),整个接触面承受的无量纲法向总载荷P*是整个接触面的接触率A*r的显函数。在机械工程实际的螺栓结合部中,哑铃状测试试件具有三种接触面:①零件1、零件2间的平面接触面;②螺栓与零件2的螺纹接触面;③螺栓头与零件1阶梯光孔的平面接触面。其中后两种接触面与螺栓的共同作用是将数显扳手控制的拧紧力矩转化为作用在整个接触面上的法向总载荷。所以按照式(53)、给定工程预紧力[24]P*,可间接计算接触率
若 K =0.5、φ = 0.01、γ =1.5 时,选择不同分形维数D及无量纲分形粗糙度G*,因变量P*对自变量的影响见图3。
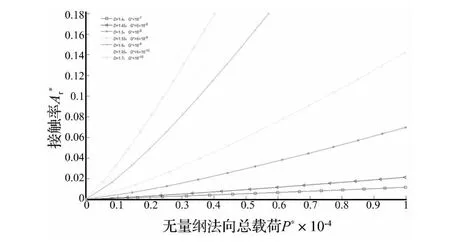
图3 接触率随无量纲法向总载荷的变化规律Fig.3 Varying law of contact ratio with dimensionless normal total load
4 静摩擦非线性特征的预测
4.1 分形维数D对静摩擦的影响
若 K=2.8、φ =1、G*=10-10、μ =0.3、γ =1.5 时,分形维数D对静摩擦特征的影响见图4。
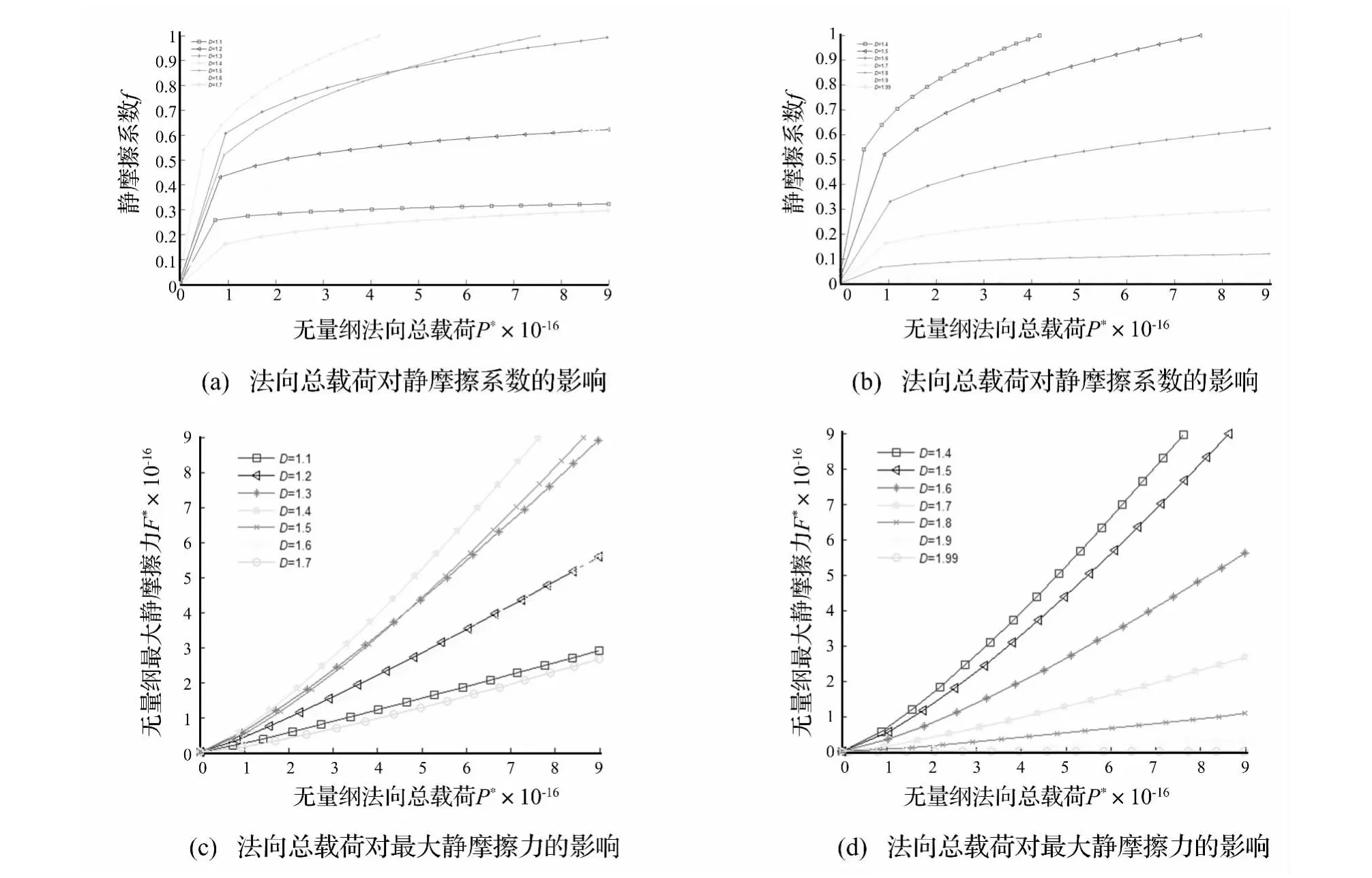
图4 分形维数对静摩擦特征的影响Fig.4 Effect of fractal dimension to static friction features
4.2 无量纲分形粗糙度G*对静摩擦的影响
若 K=2.8、φ =1、μ =0.3、γ =1.5 时,无量纲分形粗糙度G*对静摩擦特征的影响见图5。
4.3 材料性能参数φ对静摩擦的影响
若 K=2.8、D=1.7、G*=10-10、μ =0.3、γ =1.5时,材料性能参数φ对静摩擦特征的影响见图6,其中图6(a)不同于文献[15]的图4(3条曲线沿顺时针方向分别对应 φ =0.01、φ =1、φ =0.1,φ =0.01 代表的曲线几乎与y轴重合)。

图5 无量纲分形粗糙度对静摩擦特征的影响Fig.5 Influence of dimensionless fractal roughness to static friction performances
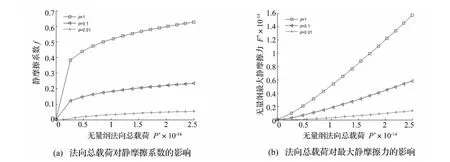
图6 材料性能参数对静摩擦特征的影响Fig.6 Impact of material property parameter to static friction traits
通过数值模拟的计算结果可以看出:
(1)依据图3,接触率随着无量纲法向总载荷的增大而增大,且表面越平整(即分形维数越大、无量纲分形粗糙度越小)接触率增大的相对比例越大。
(2)由图4(a)~4(b)、图5(a)~5(d)、图6(a)可知,静摩擦系数随着无量纲法向总载荷的增大而微向上凸弧式增大,并无限接近于1,这是由于随着法向总载荷增大,润滑油的挤压损失随之加大,摩擦副表面油膜变薄,进入混合润滑状态,摩擦表面接触微突起增多,法向总载荷一部分由油膜承担,一部分由接触微突起承担,其摩擦学特征由润滑油的流变学和接触微突起的弹塑性变形共同决定,本文论断与文献[4]中结论“静摩擦系数随着无量纲法向总载荷的增大而微向上凹弧式减小”、文献[6]的论断“静摩擦系数随着无量纲法向总载荷的增大而微向上凸弧式减小”恰恰相反,与文献[25]中有关结果“静摩擦系数随着无量纲法向总载荷的增大而微向上凹弧式增大”稍有不同,这是因为文献[25]在无量纲法向总载荷表示的横坐标中采用常用对数刻度,而本文在无量纲法向总载荷表示的横坐标中使用绝对刻度。
(3)当φ=1时,由图4(a)分析可知,在1.1≤D≤1.4范围内,静摩擦系数随着分形维数的增大而增大;从图4(a)~4(b)可以看出,在1.4≤D≤1.99范围内,静摩擦系数随着分形维数的增大而下降,故分形维数存在某个最优数,该数让静摩擦系数取得极大值。
(4)传统摩擦学观点认同,降低表面粗糙度,可以改善摩擦性能——降低静摩擦系数。但按照图5(a)~5(d)分析可知,静摩擦系数随着无量纲分形粗糙度的减小而微向上凸弧式增加,当表面粗糙度降低到一定程度,达到超光洁状态时,摩擦副的摩擦性能反而下降。
(5)通过图6(a)分析可知,静摩擦系数f随φ的增加而微向上凸弧式增加,这和文献[11]的言论“f随φ的增加而降低”差异很大。
(6)理想的Coulomb干摩擦模型认定,静摩擦系数与法向总载荷无关,法向总载荷越大,最大静摩擦力会变大。从图4(c)~4(d)、图5(e)~5(h)、图6(b)可知,法向总载荷和最大静摩擦力近似呈现出线性正比例的关系,验证经典摩擦学论点。
5 结论
(1)基于各向异性分形几何理论,提出一种摩擦非线性数学模型,研究表明该模型可以用于进行摩擦非线性特征的预测。
(2)静摩擦系数不像理想的Coulomb干摩擦模型描述那样为恒定值,它由两接触材料的分形维数D、分形粗糙度G、域扩展因子ψ、相关因子K、材料性能参数φ、表面轮廓频谱密度相关的参数γ与法向总载荷P一起决定。
(3)静摩擦系数随着法向总载荷、材料性能参数的增大而微向上凸弧式增大,但随着分形粗糙度的减小而微向上凸弧式增加。
(4)当分形维数较小时,静摩擦系数随着分形维数的增大而增大;当分形维数较大时,静摩擦系数随着分形维数的增大而变小。
(5)在绝对刻度坐标系下,法向总载荷和最大静摩擦力近似呈现出线性正比例的关系。
[1] Peitgen H O.Benoi^t B mandelbrot(1924-2010)[J].Science,2010,330(6006):926.
[2] Gomory R.Benoi^t mandelbrot(1924-2010)[J].Nature,2010,468:378.
[3]谢伯元,张 琦,鲁毅飞,等.紧急制动摩擦片的摩擦因数研究[J].农业机械学报,2006,37(12):33 -35.XIE Bo-yuan,ZHANG Qi,LU Yi-fei,et al.Research on friction coefficient of drum brake’s lining based on urgency brake course[J].Transactions of the Chinese Society for Agricultural Machinery,2006,37(12):33 -35.
[4] Chang W R,Etsion I,Bogy D B.Static friction coefficient model for metallic rough surfaces[J].ASME Journal of Tribology,1988,110(1):57 -63.
[5]Greenwood JA,Williamson J B P.Contact of nominally flat surfaces[J].Proceedings of the Royal Society of London:Series A Mathematical and Physical Sciences,1966,295(1442):300-319.
[6]尤晋闽,陈天宁.结合面静摩擦系数的统计模型[J].振动与冲击,2010,29(12):26 -29,235.YOU Jin-min,CHEN Tian-ning.Statistical model of static friction coefficient between joint surfaces[J].Journal of Vibration and Shock,2010,29(12):26 -29,235.
[7 ] Ibrahim R A.Friction-induced vibration,chatter,squeal,and chaos partⅠ:mechanics of contact and friction[J].Applied Mechanics Reviews,1994,47(7):209 -226.
[8 ] Ibrahim R A.Friction-induced vibration,chatter,squeal,and chaos partⅡ:dynamics and modeling[J].Applied Mechanics Reviews,1994,47(7):227 -253.
[9]王国强,马若丁,刘巨元,等.金属摩阻材料间摩擦系数与滑动速度关系的研究[J].农业工程学报,1997,13(1):35-38.WANG Guo-qiang,MA Ruo-ding,LIU Ju-yuan,et al.Study on the coefficient of dynamic friction between frictional metal material[J]. Transactions of the Chinese Society of Agricultural Engineering,1997,13(1):35 -38.
[10]马晨波,朱 华,孙见君.考虑粗糙度影响的表面织构最优参数设计模型[J].华中科技大学学报(自然科学版),2011,39(8):14 -18,35.MA Chen-bo,ZHU Hua,SUN Jian-jun.Optimal design model of surface texture with surface roughness considered[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition),2011,39(8):14 -18,35.
[11]盛选禹,雒建斌,温诗铸.基于分形接触的静摩擦系数预测[J].中国机械工程,1998,9(7):16 -18.SHENG Xuan-yu, LUO Jian-bin, WEN Shi-zhu. Static friction coefficient model based on fractal contact[J].China Mechanical Engineering,1998,9(7):16 -18.
[12] Majumdar A,Bhushan B.Fractal model of elastic-plastic contact between rough surfaces[J].ASME Journal of Tribology,1991,113(1):1 -11.
[13]田红亮,朱大林,秦红玲.固定接触界面法向静弹性刚度的改进弹簧分形模型[J].三峡大学学报(自然科学版),2012,34(6):83 -88.TIAN Hong-liang,ZHU Da-lin,QIN Hong-ling.Improved spring fractal model for normal static elastic stiffness of stationary contact interface[J].Journal of China Three Gorges University(Natural Sciences),2012,34(6):83 -88.
[14] Tian H L,Li B,Liu H Q,et al.A new method of virtual material hypothesis-based dynamic modeling on fixed joint interface in machine tools[J].International Journal of Machine Tools & Manufacture,2011,51(3):239 -249.
[15]兰国生,张学良,丁红钦,等.基于分形理论的结合面静摩擦因数改进模型[J].农业机械学报,2012,43(1):213-218.LAN Guo-sheng,ZHANGXue-liang,DINGHong-qin,et al.Modified model of static friction coefficient of joint interfaces based on fractal theory[J].Transactions of the Chinese Society for Agricultural Machinery,2012,43(1):213 -218.
[16] Yan W,Komvopoulos K.Contact analysis of elastic-plastic fractal surfaces[J].Journal of Applied Physics,1998,84(7):3617-3624.
[17]田红亮,赵春华,朱大林,等.弹塑性三维各向异性分形表面的接触分析[J].三峡大学学报(自然科学版),2012,34(1):69-73.TIAN Hong-liang,ZHAO Chun-hua,ZHU Da-lin,et al.Contact analysis of elastoplastic three-dimensional anisotropic fractal surfaces [J]. Journal of China Three Gorges University(Natural Sciences),2012,34(1):69 -73.
[18]黄晓乐,周正军,许文年.植被混凝土基材2中草本植物根-土复合体抗剪强度与根系分形特征研究[J].三峡大学学报(自然科学版),2012,34(2):59 -62.HUANG Xiao-le, ZHOU Zheng-jun, XU Wen-nian.Research on shear strength and fractal feature of root-soil composite system by two herb plants in vegetation-growing concrete matrix [J]. Journal of China Three Gorges University(Natural Sciences),2012,34(2):59 -62.
[19]温诗铸,黄 平.摩擦学原理[M].4版.北京:清华大学出版社,2012:30,219.
[20]Wang S,Komvopoulos K.A fractal theory of the interfacial temperature distribution in the slow sliding regime:partⅠ—elastic contact and heat transfer analysis[J].ASME Journal of Tribology,1994,116(4):812 -823.
[21]田红亮,朱大林,秦红玲.结合面静摩擦因数分形模型的建立与仿真[J].应用力学学报,2011,28(2):158 -162.TIAN Hong-liang,ZHU Da-lin,QIN Hong-ling.Fractal model of static friction coefficient of joint interface and its simulation [J].Chinese Journal of Applied Mechanics,2011,28(2):158 -162.
[22] Bhushan B.Analysis of the real area of contact between a polymeric magnetic medium and a rigid surface[J].ASME Journal of Tribology,1984,106(1):26 -34.
[23]魏 龙,刘其和,张鹏高.基于分形理论的滑动摩擦表面接触力学模型[J].机械工程学报,2012,48(17):106 -113.WEI Long,LIU Qi-he,ZHANG Peng-gao.Sliding friction surface contact mechanics model based on fractal theory[J].Journal of Mechanical Engineering,2012,48(17):106 -113.
[24]田红亮,刘芙蓉,朱大林.4种NET欧拉-伯努利直梁的动力学特性[J].三峡大学学报(自然科学版),2013,35(4):85-93.TIAN Hong-liang, LIU Fu-rong, ZHU Da-lin. Dynamic properties of four NET euler-bernoulli straight beam [J].Journal of China Three Gorges University (Natural Sciences),2013,35(4):85 -93.
[25]田红亮,赵春华,方子帆,等.金属材料表面静摩擦学特性的预测研究——理论模型[J].振动与冲击,2013,32(12):40 -44,66.TIAN Hong-liang,ZHAO Chun-hua,FANG Zi-fan,et al.Predication investigation on static tribological performance of metallic material surfaces—theoretical model[J].Journal of Vibration and Shock,2013,32(12):40 -44,66.
