滑动轴承－转子系统不平衡－不对中－碰摩耦合故障动力学建模及响应信号分解

肖 汉，周建中，肖 剑，夏 鑫，张炜博，付文龙

碰摩是旋转机械动、静件之间发生接触、摩擦所产生的一种动力学现象，其振动响应过程复杂，具有较强的非线性特征［1］。碰摩故障常由不平衡、不对中、基础松动等引起，是导致转子系统失稳的重要原因之一。因此，对碰摩耦合故障进行建模与分析，探索耦合故障间的相互作用关系，有助于碰摩故障的及时发现与诊断，具有重要意义。

国内外学者［2－7］对此进行了大量研究。Muszynska等［2］研究了不平衡和松动、碰摩耦合故障作用下转子系统的混沌响应，Shen等［3］研究了不平衡作用下转子轴承系统的碰摩响应，黄志伟等［4］对水轮发电机组转子不对中－碰摩耦合故障进行了动力学分析，曲秀秀等［5］建立了不平衡－碰摩－松动耦合故障的转子动力学模型，并对其振动响应的盲分离进行了研究，张俊红等［6］进行了不平衡－碰摩－不对中故障耦合作用下柔性转子－滚动轴承系统动力学分析与实验研究，陈果等［7］对航空发动机整机振动中的不平衡－不对中－碰摩耦合故障进行了动力学建模与仿真。

然而，在以往研究中，针对滑动轴承－转子系统中不平衡－不对中－碰摩耦合故障动力学特性的研究尚显不足。在滑动轴承－转子系统中，转子在轴承处受到非线性油膜力的影响，使得耦合故障作用下系统的动力学特性更为复杂。本文针对滑动轴承－转子系统，在Jeffcott转子模型的基础上，将两端视为滑动轴承支承，引入非线性油膜力模型，并综合考虑不平衡、不对中和碰摩故障的耦合作用，建立了非线性油膜力作用下，滑动轴承－转子系统的不平衡－不对中－碰摩耦合故障模型，仿真系统振动响应，并在多功能转子试验台上进行了不平衡－不对中－碰摩耦合故障实验，验证了模型的有效性。同时，针对耦合故障振动响应多频率信号混叠的现象，提出了一种微分耦合经验模态分解(Differential Coupling EMD，DCEMD)方法，对系统振动响应进行分解，并从中分析各耦合故障对系统响应的影响及其时频特征。研究结果为滑动轴承－转子系统的故障诊断提供有力理论依据和技术支撑。

1 不平衡－不对中－碰摩耦合故障动力学建模

1.1 系统动力学模型

本文在Jeffcott转子模型基础上，将其两端视为相同的滑动轴承支承，并借鉴文献［7－8］中提出的各故障模型，建立了一种非线性油膜力作用下滑动轴承－转子系统的不平衡－不对中－碰摩耦合故障模型，模型示意图如图1所示。其中，Op为转子几何中心，Oe为转子质心，Ol和Or分别为左右两轴承的几何中心;mp为转子在圆盘处等效质量;k为弹性轴的刚度，kr为碰摩刚度;cp和cr分别为转子在圆盘与轴承处的阻尼系数;δ为定、转子之间的间隙;Δl为联轴器间距，Δy为平行不对中量，Δα为夹角不对中量;ω为转子系统转速;e为质量偏心量;Folx、Foly、Forx、Fory分别为左右两端轴承处受到的非线性油膜力;Fcx和Fcy为转子系统受到的等效不对中力;PN和PT为碰摩力。

本文采用有限元分析的方法对滑动轴承－转子系统进行仿真［9－11］，将系统划分为如图2所示的11个轴单元，所对应n个截面如图所示。设系统运动状态向量 u=［x1y1θx1θy1x2y2θx2θy2… xnynθxnθyn］T，非线性油膜力作用下，不平衡－不对中－碰摩耦合故障的转子系统模型如下:

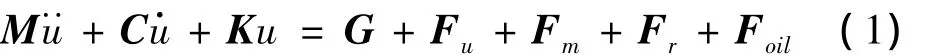
其中:M、C、K分别为系统质量、阻尼和刚度矩阵，具体形式参考文献［9 －11］，在此从略。G、Fu、Fm、Fr和 Foil分别为系统受到的重力矢量、不平衡力矢量、不对中力矢量、碰摩力矢量和非线性油膜力矢量:

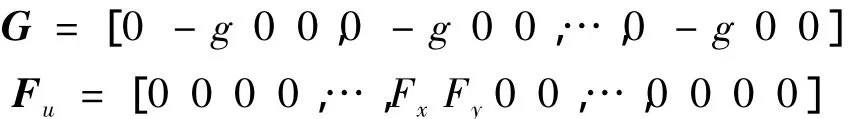
式中:Fx、Fy、Px、Py分别为不平衡力和碰摩力在 x、y 方向上的分量。

图1 滑动轴承－转子系统不平衡－不对中－碰摩耦合故障动力学模型示意图ig.1 Dynamic model of sliding bearing-rotor system with unbalance-misalignment-rubbing coupling faults

图2 滑动轴承－转子系统有限元示意图Finite element sketch of the sliding bearing－rotor system

1.2 不平衡故障模型

转子圆盘由于质量偏心，在旋转过程中将产生不平衡力，其大小与转盘质量mp、偏心距e、初始不平衡相位θ及转速ω有关:

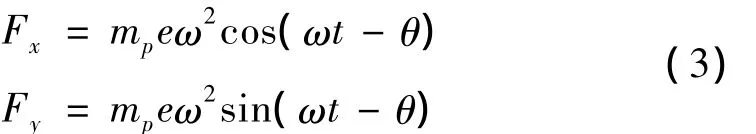
1.3 不对中故障模型

本文模型主要考虑联轴器不对中，其中包括偏角不对中、平行不对中以及综合不对中三种情况。当通过联轴器连接的主、从转子轴线不对中时，受到两个半联轴器绕各自轴线旋转的限制，联轴器壳体被迫绕其中心做圆周运动，其运动轨迹可由式(4)表示［6－7］:

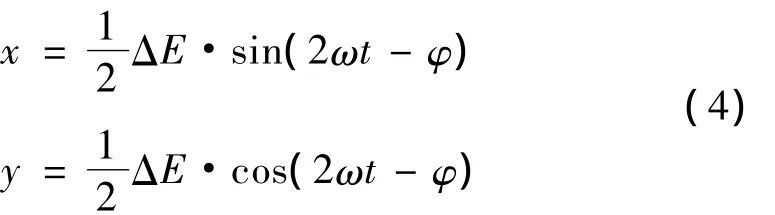
其中:ω为转速，φ为不对中初始相位，ΔE为当量不对中量，由联轴器间距Δl、平行不对中量Δy以及夹角不对中量 Δα 决定:ΔE=Δy+Δl·tan(Δα/2)。

通过联轴器壳体的运动轨迹，可以推出其运动的加速度，进而根据牛顿定律得出等效不对中力:

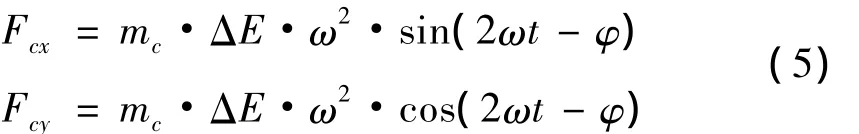
式中mc为联轴器壳体的质量。

1.4 碰摩故障模型

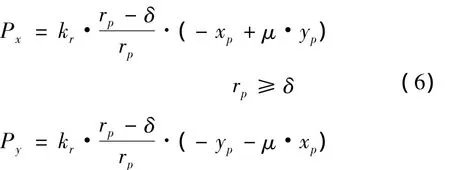
式中:kr为碰摩刚度，δ为定转子之间的间隙，μ为摩擦系数。

1.5 非线性油膜力模型

在滑动轴承－转子系统中，轴承与轴颈之间存在着距离为δs的间隙，由润滑油填充形成油膜，其流体动压力即油膜力使轴颈有足够的承载能力［12］。本文油膜力的建模采用Capone提出了圆柱瓦短轴承非线性油膜力的解析模型［13－14］:

式中:

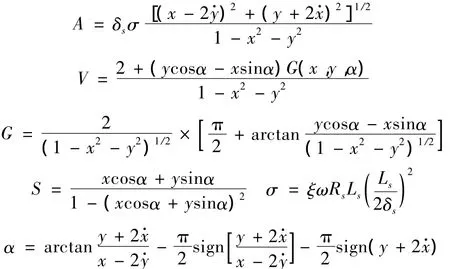
其中:ξ为润滑油粘度，Rs为轴承半径，Ls为轴承长度，x和y分别为无量纲化后的轴颈位移，分别取x=xl/δs，y=yl/δs和 x=xr/δs，y=yr/δs，即可得到左右轴承处受到的油膜力Folx、Foly和Forx、Fory。油膜力详细推导过程参考文献［13－14］，此处从略。

2 微分耦合经验模态分解

经验模态分解(Empirical Mode Decomposition，EMD)是Huang提出的一种适用于非平稳信号的自适应处理方法［15］，可将信号分解为一系列本征模式分量(Intrinsic Mode Function，IMF)，进而描述信号的时频特性。利用EMD对多频率混叠的复杂信号进行处理，可以自适应的按照不同时间尺度分离出各频率分量，便于信号特征的获取与分析。

然而传统EMD存在着频率混叠、虚假分量等问题［16－17］，为此本文提出了一种微分耦合经验模态分解(DCEMD)方法。该方法利用微分对混叠信号中能量较低的高频分量进行加强，对微分后的信号进行EMD分解，并通过积分还原，继而对各分量进行耦合经验模态分解获得原始信号的本征模式分量集，最后利用相关系数法［17］从中消除虚假分量，从而有效改善频率混叠、虚假分量的问题。DCEMD的具体步骤如下:

(1)对原始信号X进行微分，并对微分后的信号进行EMD分解，得到微分本征模式分量集DIMF={dimf(i)，i=1，2，…，n};

(2)对各DIMF进行积分还原，获得原始信号的初始本征模式分量集 OIMF={oimf(i)，i=1，2，…，n}，初始化循环变量cycle=1;

(3)对OIMF进行耦合EMD分解:当cycle＜n时，首先对oimf(cycle)进行一阶EMD，得到两个临时本征模式分量TIMF1和TIMF2，然后将TIMF1作为原始信号X的第cycle个本征模式分量，即imf(cycle)=TIMF1，最后将 TIMF2叠加在下一个 OIMF分量 oimf(cycle+1)，并执行cycle+1;

(4)循环结束，对最后一个OIMF分量oimf(n)作EMD，并将结果添加到原始信号的本征模式分量集IMF中。

(5)利用相关系数法对IMF中虚假分量进行消除，得到最终的DCEMD本征模式分量集。

3 耦合故障仿真结果分析

本文利用所建立的耦合故障模型，对滑动轴承－转子系统中非线性油膜力作用下的不平衡、不对中、碰摩耦合故障进行了仿真，并利用DCEMD对其振动响应进行了分析。本文模型参数均依照CUT－2型转子试验台设定，具体参数设定如下:转子及转轴的密度ρ=7 850 kg/m3，轴的弹性模量 E=2.1 ×1011Pa，偏心距 e=0.1 mm，不平衡初始相位θ=30°，联轴器间距Δl=1 mm，平行不对中量Δy=0.1 mm，夹角不对中量Δα=0.1 rad，联轴器壳体的质量mc=0.1 kg，不对中初始相位φ=0.3 rad，碰摩间隙 δ=0.05 mm，碰摩刚度 kr=13×104N/m，摩擦系数μ=0.1，轴承轴颈间隙δs=2 mm，轴承长度Ls=40 mm，润滑油粘度 ξ=2.5 ×10－3Pa·s。此外，仿真模型中的转子系统各轴段长度与直径如表1所示。

耦合故障模型在圆盘位置的振动响应如图3所示，其中(a)、(b)分别为圆盘处X向和Y向摆度波形，(c)为圆盘处轴心轨迹。显然，转子摆度信号为多频信号的混合，较为复杂，难于直观的分析出各故障对系统振动响应的影响。图4(a)和(b)分别为转子X和Y向摆度信号消除虚假分量之后的主要本征模式分量，从中可以看出:X和Y向摆度信号经过分解后均得到两个主要本征模态分量，其中IMF2为一、二倍频信号的混合，而IMF1则为其他频率信号的混合，分解结果存在较为严重的频率混叠现象，尤其是对摆度信号中能量较高的一、二倍频信号无法实现有效的分离。

表1 滑动轴承－转子系统仿真主要参数Tab.1 The main parameters of the sliding bearing-rotor system

图3 耦合故障模型仿真振动响应Fig.3 The simulation vibration response of the coupling faults model

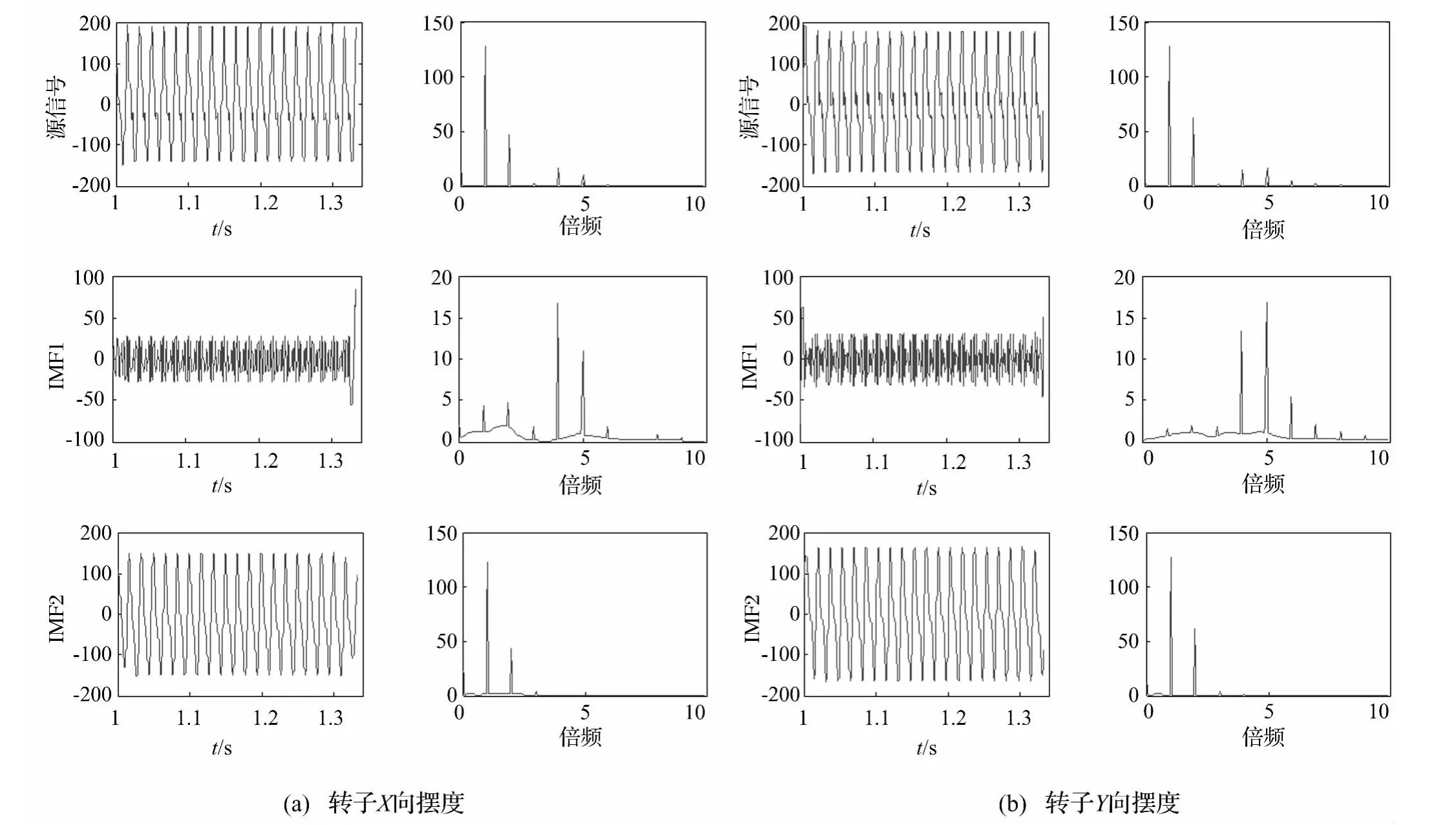
图4 仿真振动响应EMD分解本征模态分量Fig.4 The EMD results of simulation vibration response

由此可见，传统EMD无法有效的完成耦合故障振动响应的分解。这是由于EMD的上下包络需要通过信号的极大极小值计算获得，当源信号中各分量频率接近或幅值相差较大时，幅值较小的高频分量可能无法产生局部极值，因此难以被分离出来。利用DCEMD对振动响应进行分解，所得结果如图5所示。转子振动响应信号被分解为三个主要本征模态分量，其中:IMF3为1倍频分量，主要表征了耦合故障中不平衡成分;IMF2为2倍频分量，主要表征了不对中故障成分;IMF3为其他倍频分量的叠加，具有明显的碰摩故障特征，表征了耦合故障中的碰摩成分。对比传统EMD，DCEMD能够将耦合故障响应混合信号中1、2倍频分量有效的分离出来，虽然3～5倍频分量仍有混叠现象，但是已经能够直观的反映出不平衡、不对中以及碰摩故障所造成的系统响应，可以作为故障征兆获取的基础。

此外，研究中发现，非线性油膜力的作用下系统产生了幅值较小的高频振动分量，会在一定程度上影响故障信号的识别。然而通过信号分离，高频分量能够与噪声信号一起被有效分离出来，进而避免非线性油膜力对系统不平衡－不对中－碰摩耦合故障主要特征识别的干扰。本文在滑动轴承－转子系统动力学分析中考虑了非线性油膜力的影响，使研究结果更接近实际情况，为耦合故障的诊断提供了更为可靠的理论依据和技术支撑。

图5 仿真振动响应DCEMD分解本征模态分量Fig.5 The DCEMD results of simulation vibration response

4 耦合故障实验结果分析

为了进一步验证耦合故障模型及信号分离方法的有效性，本文利用CUT－2型转子试验台进行了不平衡、不对中、碰摩耦合故障的模拟试验，并利用DCEMD对实际信号进行分解。

转子实验台故障模拟如图6所示:在转盘中加入螺钉，使转盘处重心偏移，模拟不平衡故障;在末端轴承下方添加垫片，使主、从两转子系统轴线产生夹角，模拟不对中故障;在转盘附近支架上设置碰摩螺栓，模拟碰摩故障。利用图6中所示的传感器布设，对转子系统X、Y向摆度进行测量，转速为3 300 r/min，采样率设为28 160 Hz，采样点数为8 192。实验所得X、Y向摆度信号及轴心轨迹如图7所示。与模型仿真结果类似，实测信号也是由多频率信号混叠而成。利用DCEMD对实测信号进行分解，图8(a)和(b)分别为转子X、Y向摆度信号去除虚假成分后的主要本征模式分量。

图6 转子实验台故障模拟图Fig.6 Fault simulation on the rotor test device

通过图8可以看出:X、Y两向摆度信号均以1倍频分量为主要成分，对应耦合故障中不平衡成分;同时X向信号含有较大的二倍频分量，对应耦合故障中不对中成分，而Y向信号2倍频分量较小，这是由转子试验台不对中的初始相位造成的;此外，两向摆度信号均含有较小的3～5倍频分量，对应耦合故障中碰摩成分。因此，实测耦合故障响应与本文所建模型仿真结果基本一致，验证了耦合故障模型的有效性。

另一方面，通过微分耦合经验模态分解:X向摆度信号中的1、2倍频分量可以比较有效的分离出来，而3～5倍频分量中含有低频分量的干扰无法有效分离;Y向摆度信号中1倍频分量可以较好的分离出来，而2倍频分量却混叠与3～5倍频分量中。这是由于耦合故障模拟实验中，外加碰摩杆的碰摩刚度较小，因此碰摩引起的高倍频振动分量幅值过小，虽然经过微分可以一定程度上得到加强，却仍无法实现完全的分离。总体而言，尽管DCEMD仍存在一定程度频率混叠的问题，但振动响应中能量较大的主要成分(X向摆度信号中的1、2倍频分量，Y向摆度信号中的1倍频分量)均能实现有效的分离。因此，利用DCEMD对信号进行分解，可以有效的分离出信号的主要成分，有助于故障特征的获取。

图7 转子台实验耦合故障振动响应Fig.7 The experimental vibration response of the rotor test device

图8 实验振动响应DCEMD分解本征模态分量Fig.8 The DCEMD results of experimental vibration response

5 结论

本文建立了非线性油膜力作用下滑动轴承－转子系统的不平衡－不对中－碰摩耦合故障模型，并在转子试验台上同时模拟三种故障，获得耦合故障的实际振动响应，通过将实测摆度信号与模型仿真结果进行对比分析，验证了模型的有效性。

同时本文提出了一种微分耦合经验模态分解方法，并利用该方法分别对耦合故障模型的仿真结果与实测信号进行分解，结果表明，相比于传统 EMD，DCEMD对混叠成分频率接近、幅值相差较大的信号更为敏感，能够更为有效的完成系统振动响应的分解，同时，DCEMD分解结果能够直观的反映出振动响应中不同故障所对应的主要成分，为耦合故障的诊断提供依据。

综上，本文建立的耦合故障模型及提出的微分耦合经验模态分解方法能够有效的反映并捕捉振动故障征兆，对旋转机械故障诊断的发展具有促进作用。

［1］闻邦椿，武新华，丁 千，等.故障旋转机械非线性动力学的理论与试验［M］.北京:科学出版社，2004.

［2］ Muszynska A，Goldman P.Chaotic response of unbalanced rotor bearing stator systems with looseness or rubs［J］.Chaos，Solitons and Fractals，1995，5(9):1683 －1704.

［3］Shen X Y，Jia J H，Hao M Z.Numerical analysis of a rubimpact rotor-bearing system with mass unbalance［J］.Journal of Vibration and Control，2007，13(12):1819 －1834.

［4］黄志伟，周建中，张勇传.水轮发电机组转子不对中_碰摩耦合故障动力学分析［J］.中国电机工程学报，2010，30(8):88－93.HUANG Zhi-wei，ZHOU Jian-zhong，ZHANG Yong-chuan.Dynamic analysis on hydraulic generator rotors with coupling faults of misalignment and rub-impact［J］.Proceedings of the CSEE，2010，30(8):88－93.

［5］曲秀秀，陈 果，乔保栋.不平衡－碰摩－松动耦合故障的转子动力学建模与盲分离研究［J］.振动与冲击，2011，30(6):74 －77，96.QU Xiu-xiu，CHEN Guo，QIAO Bao-dong.Signal separation technology for dynamic model of rotor with unbalance-rubbinglooseness couped faults［J］.Journal of Vibration and Shock，2011，30(6):74 －77，96.

［6］张俊红，马 梁，马文朋，等.不平衡－碰摩－不对中故障耦合作用下柔性转子－滚动轴承系统动力学分析与实验［J］.天津大学学报，2012，45(10):855 －864.ZHANG Jun-hong， MA Liang， MA Wen-peng， et al.Experiment and dynamic analysis of flexible rotor-ball-bearing system with unbalance-rubbing-misalignment coupling faults［J］.2012，45(10):855－864.

［7］陈 果，李兴阳.航空发动机整机振动中的不平衡－不对中－碰摩耦合故障研究［J］.航空动力学报，2009，24(10):2277－2284.CHEN Guo，LI Xing-yang.Study on imbalance-misalignmentrubbing coupling faults in aero-engine vibratio［J］.Journal of Aerospace Power，2009，24(10):2277 －2284.

［8］陈 果.具有不平衡－碰摩耦合故障的转子－滚动轴承系统非线性动力学研究［J］.振动与冲击，2008，27(4):43－48.CHEN Guo.Nonlinear dynamic study on a rotor-ball bearing system with unbalance-rubbing coupling fault［J］.Journal of Vibration and Shock，2008，27(4):43－48.

［9］Han Q，Zhang Z，Wen B.Periodic motions of a dual－disc rotor system with rub-impact at fixed limiter［J］.Journal of Mechanical Engineering Science，2008，222:1935－1946.

［10］Chu F L，Lu W.Determination of the rubbing location in a multi-disk rotor system by means of dynamic stiffness identification［J］.Journal of Sound and Vibration，2001，248(2):235－246.

［11］ Beatty R F，Differentiating rotor response due to radial rubbing［J］.Journal of Vibration，Acoustics，Stress，and Reliability in Design，1985，107:151－160.

［12］钟一谔，何衍宗，王 正，等.转子动力学［M］.北京:清华大学出版社，1987.

［13］ Adiletta G，Guido A R.Chaotic motions of a rigid rotor in short journal bearings［J］.Nonlinear Dynamic，1996，10(3):251－269

［14］黄志伟.基于非线性转子动力学的水轮发电机组振动机理研究［D］.武汉:华中科技大学，2011.

［15］ Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proceedings of the Royal Society of London.Series A:Mathematical，Physical and Engineering Sciences，1998，454(1971):903－995.

［16］郭 奇，刘卜瑜，史立波，等.基于二次EEMD的Wigner-Ville分布旋转机械故障信号分析及试验研究［J］.振动与冲击，2012，31(13):129－133.GUO Qi，LIU Bu-yu，SHI Li-buo，et al.Experimental study and fault signals analysis of rotating machinery based on dual EEMD and wigner-ville distribution［J］.Journal of Vibration and Shock，2012，31(13):129－133.

［17］林 丽，余 轮.基于相关系数的 EMD改进算法［J］.计算机与数字工程，2008，36(12):28－36.LIN Li， YU Luen. Improvement on empirical mode decomposition based on correlation coefficient［J］.Computer and Digital Engineering，2008，36(12):28－3.