钢筋混凝土箱型墩延性抗震性能研究

夏樟华，宗周红

钢筋混凝土桥梁的延性抗震分析方法主要是通过桥墩的单向拟静力试验以及相应的理论分析建立起来的。典型的研究有Priestley和Park［1］对多种截面、不同箍筋形式桥墩的单轴加载和拟静力试验研究。Watson等［2］验证了配置不同箍筋柱的延性和强度的理论方法，提出了潜在塑性铰区域长度的计算公式。Park等学者的研究成果奠定了桥梁延性抗震设计基础。钢筋混凝土桥梁延性抗震设计方法在新西兰、日本和美国抗震设计规范中［3－5］得到应用。

我国在钢筋混凝土桥墩抗震性能方面也开展了研究。杨新宝［6］针对城市高架桥梁中钢筋混凝土柱式桥墩，以配筋率、配箍率、混凝土强度、轴压比等为参数，进行了10根截面尺寸为20 cm×20 cm钢筋混凝土矩形墩模型拟静力试验研究。范立础，卓卫东［7］选择混凝土标号、配箍率、纵筋配筋率和轴压比作为研究参数，进行了16个截面尺寸为20 cm×20 cm的钢筋混凝土墩拟静力试验，研究了钢筋混凝土桥墩塑性铰区范围内的约束箍筋含量与构件延性水平之间的关系。这些研究结合国外相应的研究成果成为我国桥梁延性抗震设计方法的基础［8］。

桥墩拟静力试验研究以实体墩为主，随着公路建设快速发展，空心截面墩得到了更加广泛地应用。如宋晓东［9］，崔海琴等［10］和郝文秀等［11］针对箱型截面墩进行了单向拟静力试验研究。

位移延性是延性抗震设计的一个重要参数。位移延性性能的理论分析方法主要有公式法、Pushover分析方法以及动力增量法［7，9］，以公式法为主。公式法是以截面弯矩曲率分析为基础，从而得到屈服位移，进而根据等效塑性铰长度，计算极限位移，求得结构的位移延性。由于公式法得到的容许曲率、位移和位移延性系数等一般都大于相应实测值，因此通过安全系数来考虑这种效应。如日本规范以位移延性系数作为延性设计指标，根据桥梁重要性和地震类型设置了不同的安全系数，其中I型地面运动的A类桥梁的安全系数为2.4［4］。中国公路桥梁抗震细则以极限塑性转角和极限位移为延性抗震的指标，其中在计算极限塑性转角考虑了2.0的安全系数［8］。另一个方面，等效塑性铰长度都是以试验为基础的经验公式来计算，各国规范的计算方法也存在差异。艾庆华等［12］选用5种常用塑性铰模型，研究了塑性铰模型对残余位移、极限曲率及曲率延性系数等性能指标进行估计的准确程度，认为剪跨比大于8的桥墩计算极限曲率小于试验值，可能会导致偏于不安全的设计结果。孙治国等［13］则基于纤维梁柱单元分析了钢筋混凝土空心墩的位移延性，认为对剪跨比大于7的墩，提高纵筋配筋率可有效增强其延性变形能力。

现行桥梁延性抗震设计方法是以桥墩单向拟静力试验为基础建立的，钢筋混凝土箱型墩位移延性性能分析也是以单向拟静力试验和理论分析为主。实际箱型墩墩高较大且可能承受多向荷载作用。因此，以现有的研究为基础，通过双向拟静力试验和理论分析，研究我国公路桥梁抗震细则［8］规定高宽比范围内(高宽比大于2.5，且小于10)和超过规定高宽比范围的钢筋混凝土箱型墩延性抗震性能分析方法。

1 箱型墩双向拟静力试验概况

取高宽比、轴压比和配箍率三个参数，共设计了14个试件，见表1。模型纵筋采用28φ8，模型墩B1～B3，B6～B14在墩底区域箍筋配置为φ6@50 mm，高度为350 mm，其它区域为φ6@100mm，模型墩B4和B5墩底区域的箍筋间距分别为70 mm和100 mm，其它区域箍筋间距分别为100 mm和150 mm，所有试件离墩底150 mm高度范围内为实心段。截面尺寸为440 mm×320 mm，空心部分为260 mm×180 mm，保护层厚度为15 mm，典型试件截面尺寸和钢筋布置见图1。其中，试件强轴方向记为X方向，弱轴方向记为Y方向。为加载需要，模型墩顶为700 mm×720 mm×540 mm的实心段，用250 mm×800 mm×1 300 mm底座固定试件。采用竖向轴力方式模拟上部结构质量，轴压比η根据公式η=N/Afcd计算，N为轴力，A为截面面积，fcd为混凝土抗压强度设计值。高宽比指试件有效高度与截面宽度的比值，有效高度指加载点至墩底的距离。纵筋配筋率指桥墩试件纵筋的截面积A1与试件的截面面积A的比值。体积配箍率指箍筋的体积与试件体积的比值。模型墩混凝土强度按C50设计，实测立方体抗压强度平均值为49.41 MPa，劈裂强度为 3.44 MPa，弹性模量为3.11×104MPa。φ6和φ8钢筋实测屈服强度分别为375.27 MPa和 326.51 MPa，极限强度分别为503.81 MPa和456.60 MPa，弹性模量分别为2.11 ×105MPa和2.12 ×105MPa。

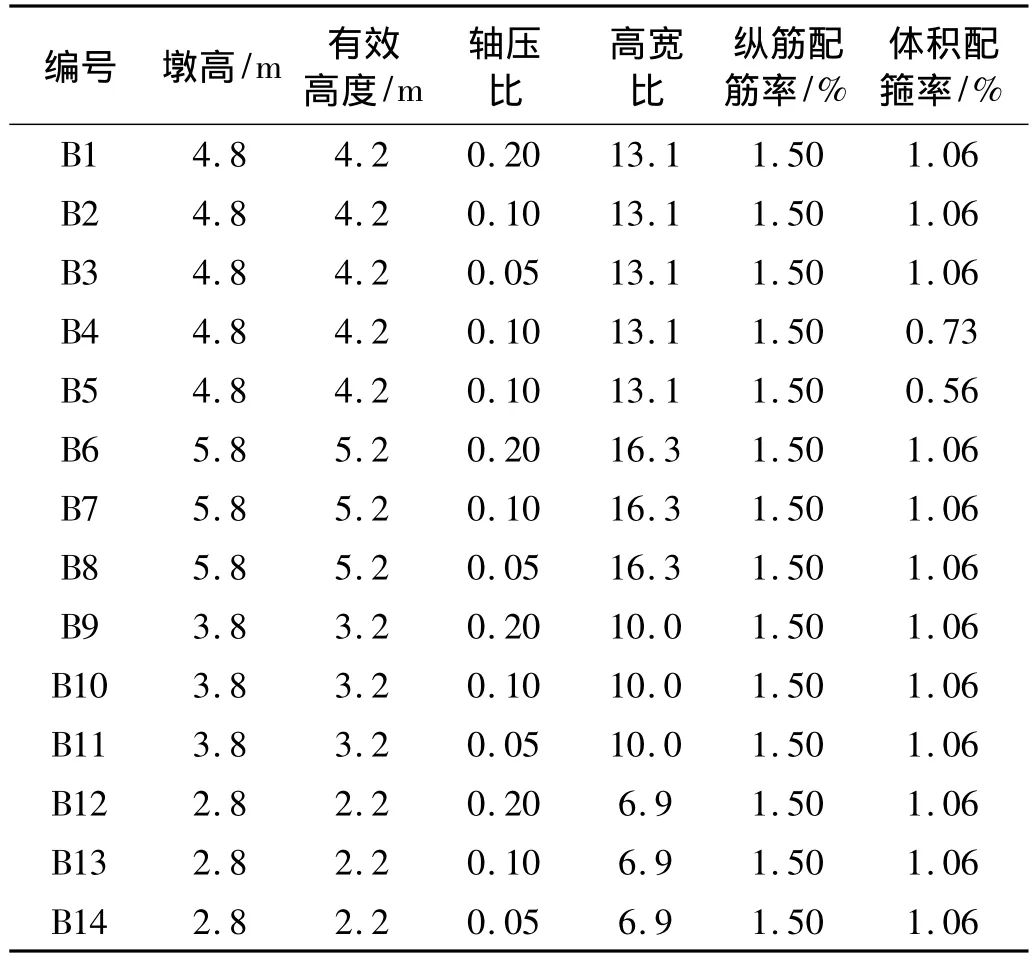
表1 桥墩试件设计参数Tab.1 Design parameters of the piers

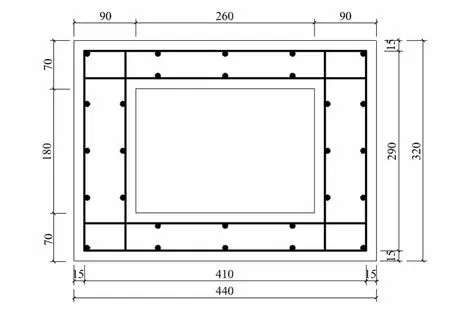
图1 典型截面和钢筋布置示意图(单位:mm)Fig.1 Reinforcement and section setup of typical test specimen(unit:mm)

试验的加载装置见图2。试验正式加载前先进行预加载，试验过程中始终在墩顶施加竖向恒定轴向荷载。水平加载采用位移控制，并且逐级施加，X方向与Y方向的位移幅值比为1∶1，每级加载循环2次。整个加载过程为:第一级加载2 mm，以后每级以2 mm的幅值递增;屈服以后，以3 mm为幅值递增加载;达到极限荷载以后，加载步长改为5 mm，直到试验结束。

试验过程中测试墩顶加载点的荷载和位移，通过测试试件截面竖向位移，换算各个区域的平均曲率［15］，共测试了离墩底高度为0.15 m，0.55 m，0.95 m 和1.35 m 四个位置的竖向位移并换算相应高度范围内的平均曲率。

图2 加载装置布置图Fig.2 Test set-up

1.1 变形实测结果分析

1.1.1 位移和位移延性

根据试验得到各个试件荷载位移骨架曲线，并将其位移特征值列于表2。结合荷载位移骨架曲线和位移特征值，比较高宽比13.1的试件B1，B2和B3，可以看出，轴压比越小，变形能力越大，见图3，比较其它三组高宽比相同轴压比不同的试件，也可以得出同样的结论。比较轴压比0.2的试件B1，B6，B9和B12，高宽比越大，试件的变形能力越小，见图4，比较轴压比0.1和0.05的两组试件也得到相同的结论。比较轴压比0.1且高宽比13.1的试件B2，B4和B5，试件体积配箍率越小变形能力越大，这与传统的中低墩的研究结果存在差异，可能的原因为墩高较大的情况下，配箍率小的墩整体刚度减小引起的极限位移的增大大于配箍率大的墩塑性转动能力增大引起的极限位移的增加。

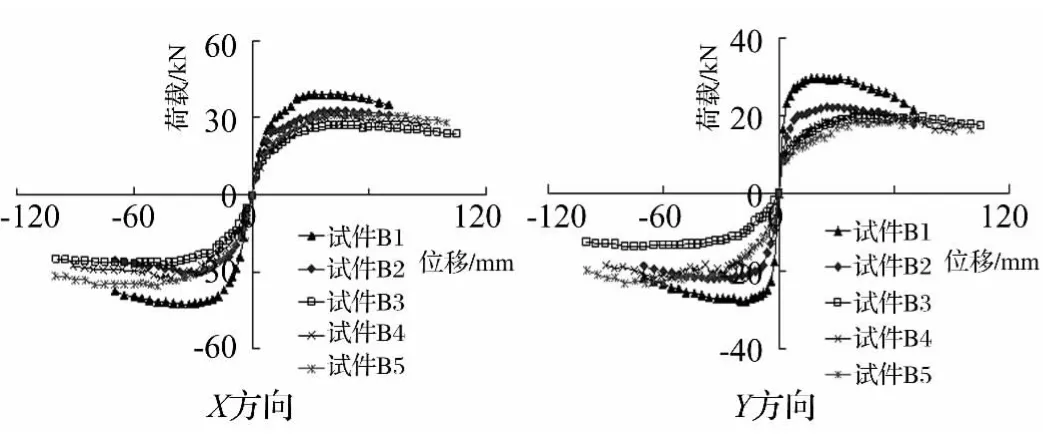
图3 试件B1、B2、B3、B4和B5的荷载－位移骨架曲线Fig.3 Load displacement skeleton curves of test specimens B1，B2，B3，B4 and B5

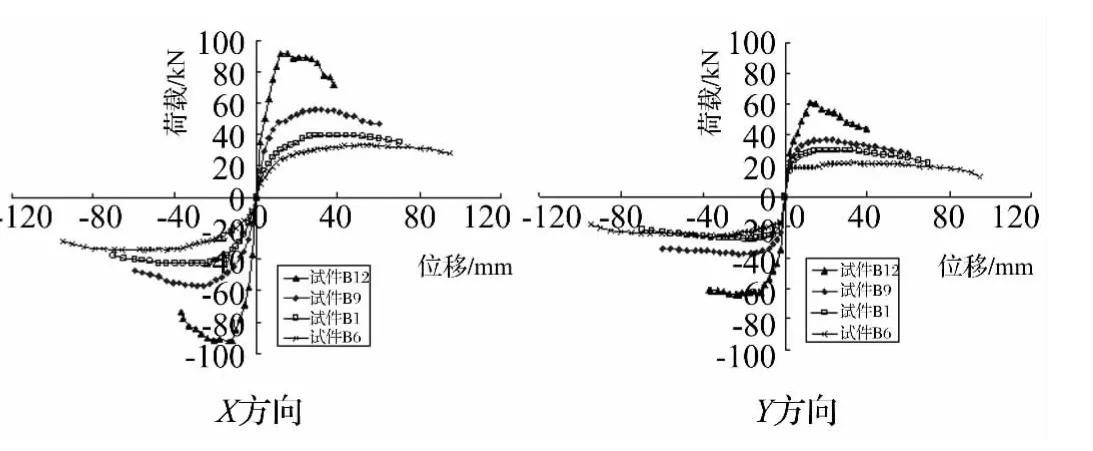
图4 试件B1、B6、B9和B12荷载－位移骨架曲线Fig.4 Load displacement skeleton curves of test specimens B1，B6，B9 and B12

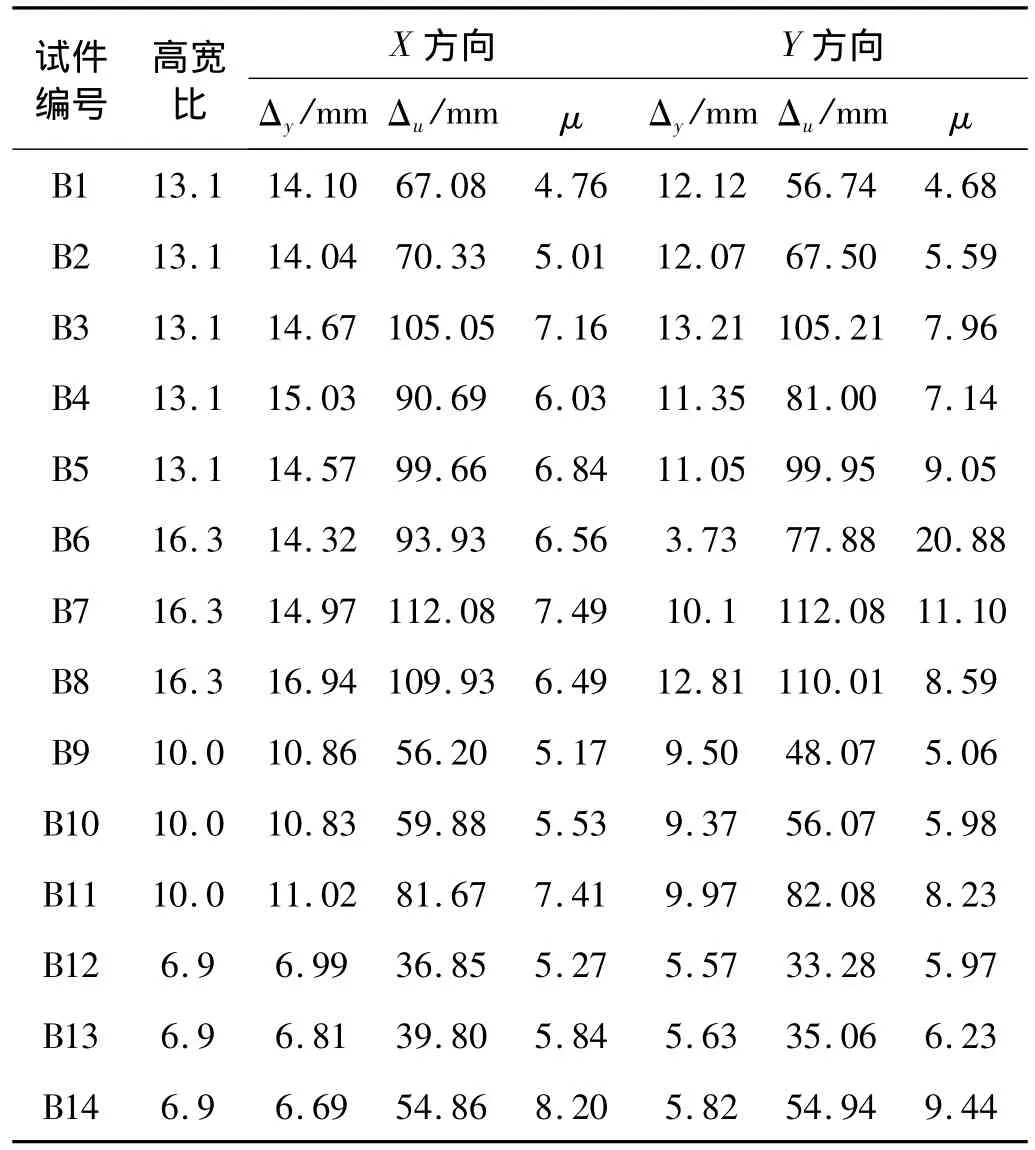
表2 桥墩试件的位移延性系数Tab.2 Displacement ductility factor of testing piers

式中:Δy为屈服位移;Δu为极限位移。

根据表2可以看出:在高宽比6.9至13.1的范围，试件X方向和Y方向的位移延性系数均随高宽比增大而减小，随轴压比的减小而增大，随体积配箍率减小而增大。但是高宽比16.3的试件的位移延性系数变化规律不同，其X和Y方向的位移延性系数基本都大于高宽比13.1的试件，且Y方向的位移延性系数随轴压比的增大而增大，主要原因是其屈位移显著降低。

1.1.2 曲率

根据实测位移，计算各荷载等级的试件曲率，以侧向位移约每增加20 mm绘制出曲率沿墩高分布。高宽比小于等于10的试件均为从墩底往上，曲率逐渐减小，见图5和图6。高宽比为13.1和16.3的试件则出现了墩高0.15 m至0.55 m范围内平均曲率明显增大的情况，试件B4，试件B6和试件B8均有这种现象，见

采用通用屈服弯曲法计算屈服位移［16］。极限位移取荷载下降至极限荷载85%对应的位移，通过式(1)求得位移延性系数，见表2。图7～图9。可以看出，高宽比越小的试件，越接近于墩底位置且截面极限曲率越大，如试件B14的X、Y方向的极限曲率明显大于试件B8的X、Y方向的极限曲率，主要原因是高宽比大的箱型墩塑性破坏区域增大，即塑性铰长度增大，可以利用的塑性转动能力相应减小。

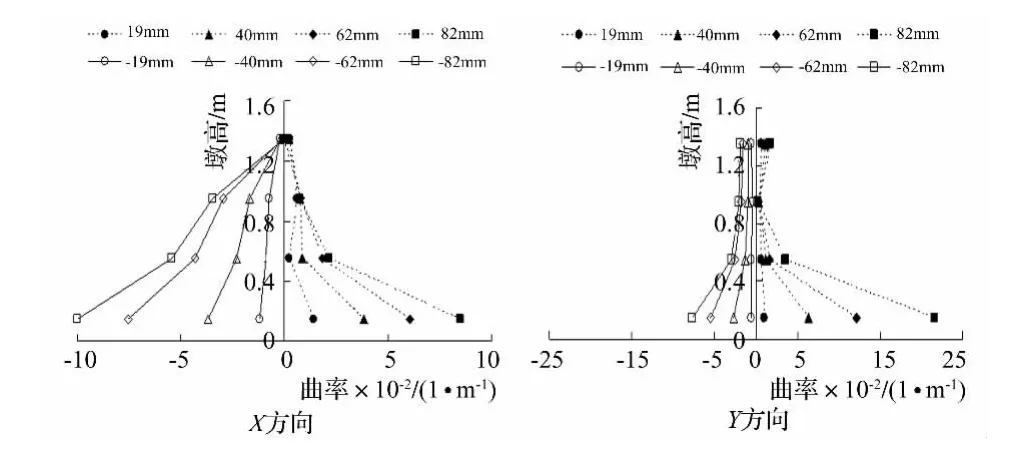
图5 试件B11曲率分布Fig.5 Curvature arrangement along height direction of specimen B11

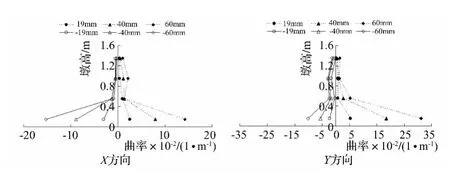
图6 试件B14曲率分布Fig.6 Curvature arrangement along height direction of specimen B14

图7 试件B4曲率分布Fig.7 Curvature arrangement along height direction of specimen B4

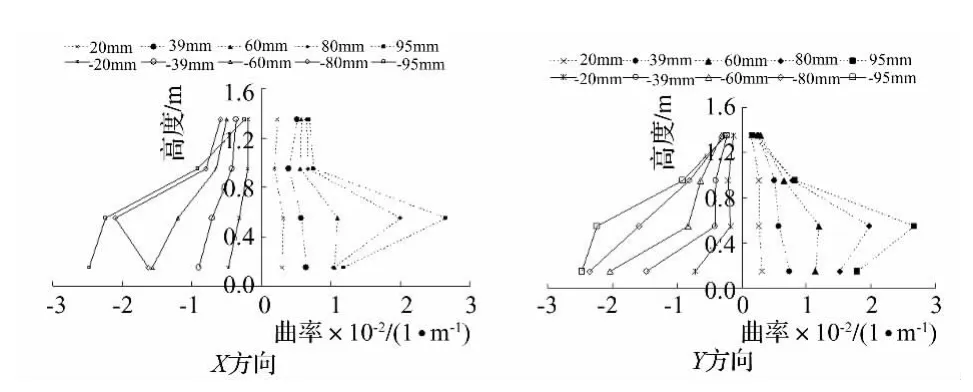
图8 试件B6曲率分布Fig.8 Curvature arrangement along height direction of specimen B6

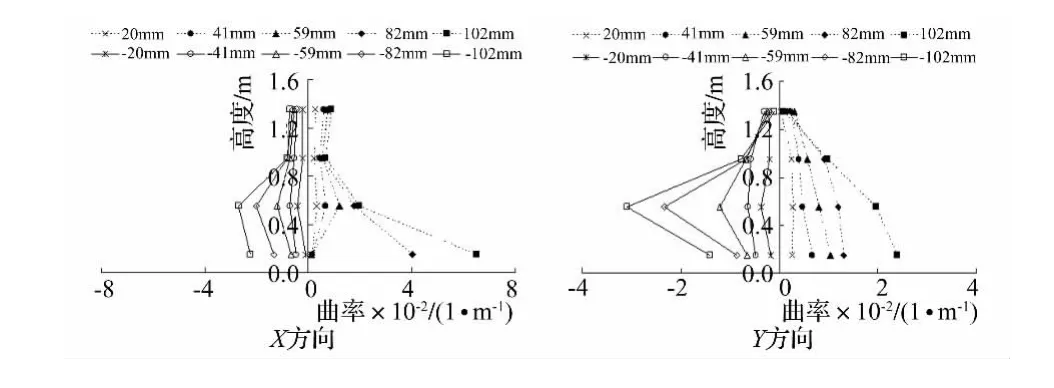
图9 试件B8曲率分布Fig.9 Curvature arrangement along height direction of specimen B8

2 双向荷载作用的钢筋混凝土箱型截面弯矩曲率分析

采用西部大学联盟“太平洋地震工程研究中心”主导、加州大学伯克利分校为主研发而成的OpenSees开放程序进行双向压弯作用的钢筋混凝土箱型截面的弯矩曲率分析［17］。为方便双向弯曲和轴压加载实现，采用非线性梁柱单元建立箱型墩模型，然后提取墩底截面的弯矩曲率。钢筋混凝土箱型墩采用非线性梁柱单元，共3个单元，每个单元设置六个积分点，墩底设为固定端，墩顶自由。

采用OpenSees程序提供的纤维截面模型，将试件截面划分为若干个细小纤维，假定试件的截面在变形过程中始终保持为平面。程序自动根据平截面假定得到每个纤维的应变，并迭代计算确保截面受力平衡。纤维模型能很好地模拟试件的弯曲和轴向变形。钢筋混凝土箱型墩的截面主要划分为保护层混凝土纤维、核心区混凝土纤维以及钢筋纤维。

混凝土本构关系采用OpenSees程序提供的混凝土的本构关系模型Concrete 02，其单轴应力－应变关系采用的是修正后的Kent-Park模型［18］，应力－应变关系见图10。该模型可通过改变混凝土受压骨架曲线的峰值应力、峰值应变以及软化段斜率来考虑横向箍筋的约束效应，混凝土受拉时上升段和下降段均为直线，可考虑混凝土的初始开裂。混凝土受压应力σc和应变εc骨架曲线可表示为:

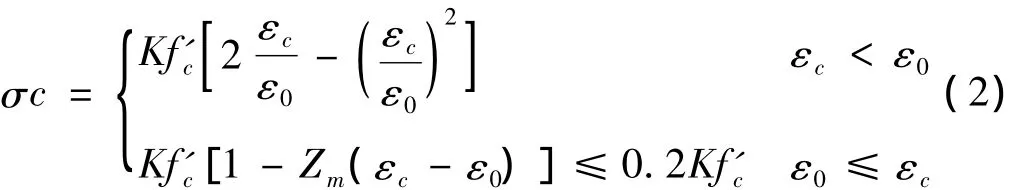
其中:ε0=0.002K，

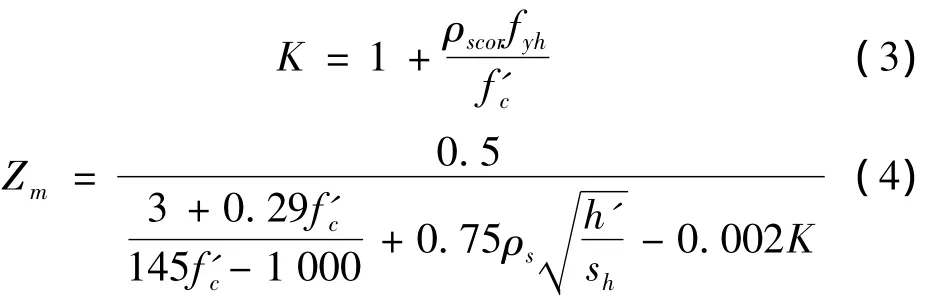
其中:K代表考虑约束所引起的混凝土强度增加系数，0.002K是相应的峰值应变;Zm是应变软化段斜率;f'c是混凝土圆柱体抗压强度(单位:MPa);fyh是箍筋的屈服强度(单位:MPa);ρscor是试件箍筋约束混凝土核心区箍筋体积配箍率;h'是从箍筋外边缘算起的核心混凝土宽度;sh是箍筋间距。

OpenSees提供了两种钢材材料的本构模型(Steel 01和Steel 02)。Steel 01模型为双线性随动强化模型，其应力－应变关系曲线如图11所示。强化段的弹性模量取为0.001Es，Es为钢筋初始弹性模量，加卸载时刚度取初始弹性模量，没有考虑软化的作用。Steel 02和Steel 01基本相同，但可以考虑等向应变硬化影响，可以通过设置材料参数来改变双线性模型中弹塑性段分支点附近的弧度变化，可以反映包辛格效应，见图11虚线部分［19］。因此，钢筋采用Steel 02材料模型，输入的主要参数:钢筋屈服强度fyh，初始弹性模量Es，应变硬化率，双线性模型中弹塑性段分支点附近弧度变化的材料参数 R0取18，CR1取0.925，CR2取0.15。

采用Newton-Raphson数值迭代方法，分析至混凝土达到极限压应变为止。其中，混凝土极限压应变εcu按照式(5)计算。

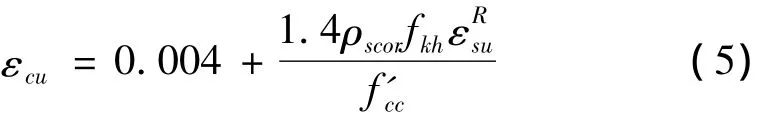
根据约束箍筋围成的混凝土矩形区域计算约束箍筋体积配筋率 ρscor，fkh为箍筋抗拉强度，取实测值，εRsu为约束钢筋的折减极限应变，取0.09，f'cc约束混凝土的峰

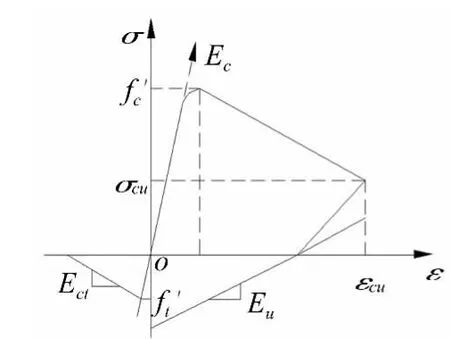
图10 Concrete 02材料模型Fig.10 Concrete 02 material model

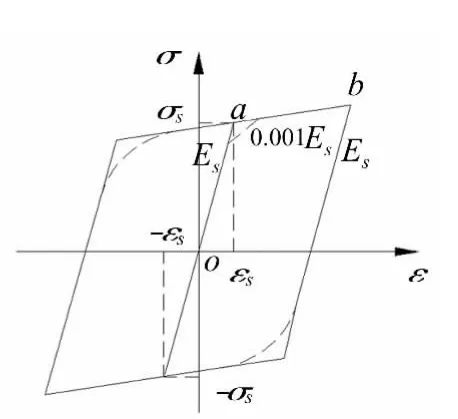
图11 钢筋材料模型Fig.11 Steel material model

3 钢筋混凝土箱型墩延性性能分析

3.1 实测和计算弯矩曲率关系

典型试件的实测和计算弯矩曲率比较见图12，实测弯矩曲率均采用正负两向绝对值的平均值。可以看出，除试件B14的实测最大弯矩略小于计算值，其余试件最大实测弯矩均大于计算弯矩且墩高越大的试件实测最大弯矩越大。除了钢筋的超强和墩底箍筋的约束效应外，参与塑性破坏的墩底范围试件长度的增大也是高宽比大于10的试件最大实测弯矩更大的原因。轴压比越大的试件实测和计算最大弯矩的差值越大。

另一个方面，模型墩截面的实测极限曲率均小于计算极限曲率。墩高越大，实测的极限曲率越小，说明墩高越大的墩截面能够发挥的塑性转动能力越小。

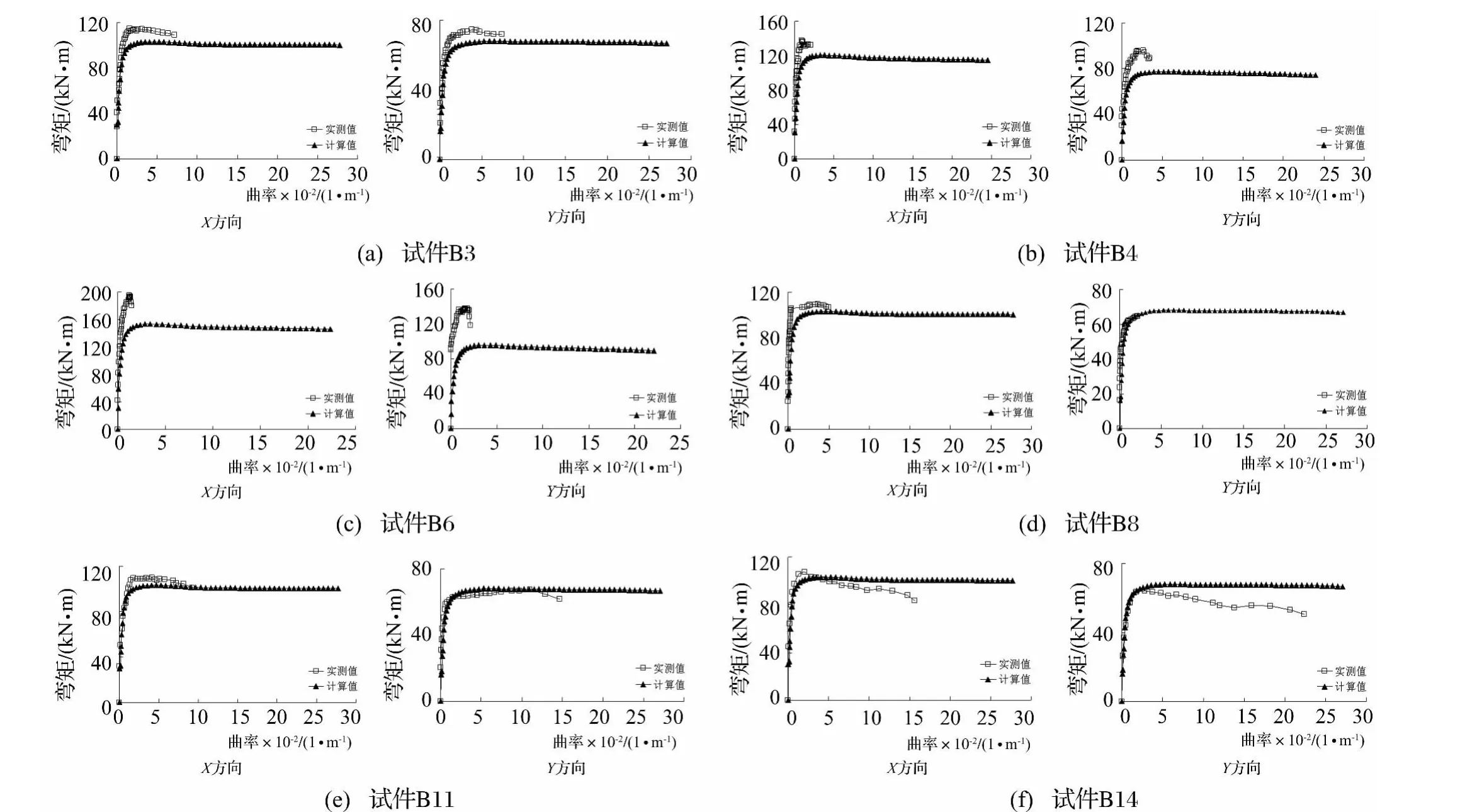
图12 实测与计算弯矩－曲率比较Fig.12 Comparison of testing and calculating moment and curvature

3.2 位移和位移延性

3.2.1 双向荷载作用箱型墩延性性能分析方法

因为高宽比13.1以内的试件实测位移延性系数与轴压比，配箍率和高宽比之间存在对应的变化关系，而高宽比16.3的试件不符合这些规律，因此只对高宽比13.1以内的钢筋混凝土箱型墩延性分析方法进行讨论。

采用通用屈服弯矩法作图得到双向压弯作用钢筋混凝土箱型墩计算屈服曲率，极限曲率取值为核心混凝土边缘达到极限压应变对应的曲率。

假定达到屈服荷载之前，曲率沿墩高呈直线分布，则箱型墩屈服时墩顶位移可以通过理论公式求解，对应的墩顶屈服位移计算公式可以表示为:

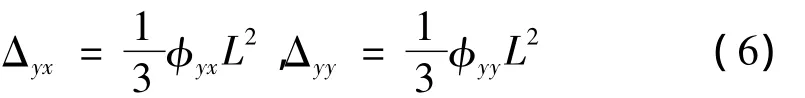
式中:Δyx和 Δyy分别为 X、Y 方向的屈服位移;φyx，φyy分别为X、Y方向的屈服曲率;L为桥墩有效加载高度。计算极限状态对应的位移，采用塑性铰长度的概念，认为在墩底附近存在一个等塑性曲率段，塑性曲率为φu，屈服曲率为φy，假定等效塑性铰长度为lp，墩的塑性转动能力θp可以表示为:

则墩顶位置的极限位移计算公式可表示为:

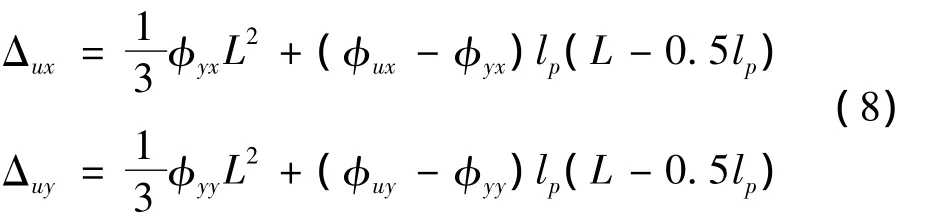
式中:Δux和Δuy分别为 X、Y方向的极限位移;φux和 φuy分别为X、Y方向的极限曲率。

根据屈服位移和极限位移，可以计算得到X方向和Y方向的位移延性系数，如式(9):

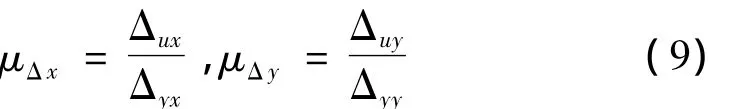
式中:μΔx和μΔy分别为X、Y方向的位移延性系数。

3.2.2 极限转角和等效塑性铰长度

一般地，通过截面分析得到的极限曲率大于实测极限曲率，因此计算的塑性转动能力可能被高估。抗震设计验算中，通过安全系数来考虑结构能够达到的塑性转动能力。在中国公路桥梁抗震细则［8］中，通过取安全系数K=2.0考虑这一因素，即最大允许的转动能力表示为:

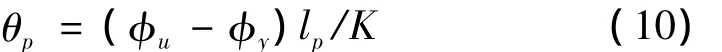
实际的实测极限曲率跟墩高、轴压和体积配箍率都有着关系，表3列出了5个墩实测与计算极限曲率与屈服曲率差值(φu－φy)的比较。根据曲率差值的比值，高宽比大于2.5且小于等于10范围内，实测与计算值的比值范围为1.5～3.2，该范围内安全系数取值为K=4.0;高宽比等于13.1，实测值与计算值的比值范围为2.5～8.9，考虑到实测极限曲率较小主要由于试件塑性区域转移到变截面以上位置引起的，所以箱型墩高宽比大于10.0小于等于13.1的情况，安全系数取值 K=7.0。

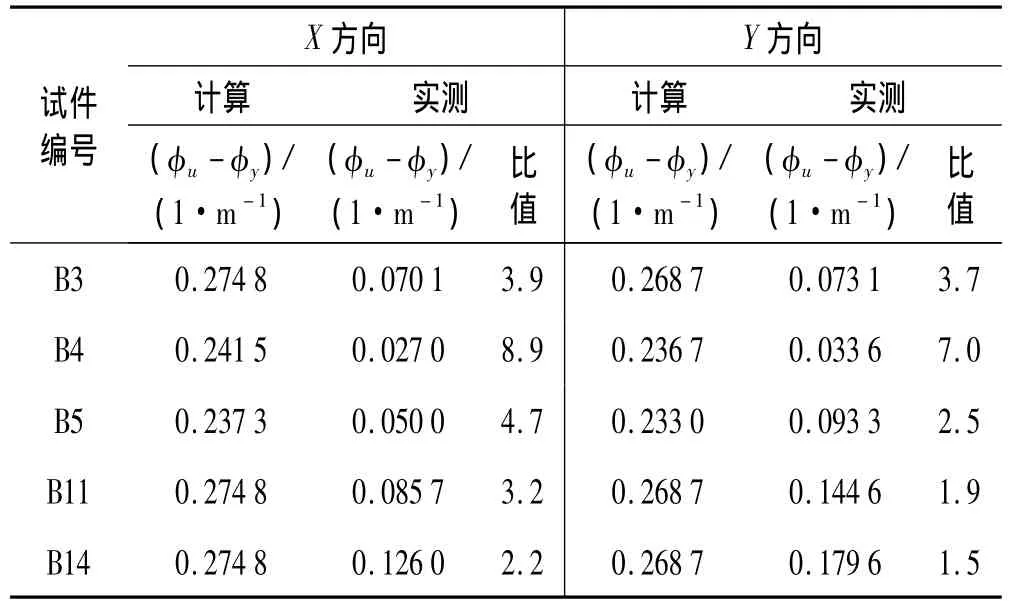
表3 计算与实测极限曲率和屈服曲率差值比较Tab.3 Comparison of testing and calculating Curvature

等效塑性铰长度lp大都以实验得到的经验公式进行估算，常用的塑性铰估算公式见表4。根据公式计算得到的塑性铰长度以及根据实测曲率和极限位移得到的等效塑性铰长度比较见表5。从计算等效塑性铰长度来看，除中国规范和日本规范的公式不能反映塑性铰长度随墩高的变化外，其它公式计算等效塑性铰长度均随墩高的增大而增加，其中式(2)和式(5)计算值比较接近，式(1)在墩高较小时计算的等效塑性铰长度较式(2)和式(5)计算值大。式(1)能反映出X、Y方向实测塑性铰长度的不同，与实测值规律一致。根据双向加载的特点，参照式(1)，考虑配箍率的影响，得到修正公式(11)计算双向荷载作用的箱型墩等效塑性铰长度的经验公式。由表5可知，根据式(11)的塑性铰计算长度与实测的塑性铰长度更为接近。

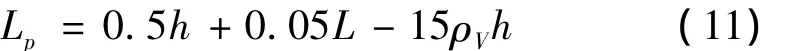
式中:h为荷载作用方向截面高度，ρV为箱型墩体积配箍率。

3.2.3 钢筋混凝土箱型墩位移延性分析结果讨论

利用式(6)～式(11)计算各试件的极限位移和位移延性系数，见表6。可以看出，计算屈服位移和极限位移总体与相应实测值接近。高宽比为13.1的试件计算位移延性系数均小于实测值，高宽比6.9和10.0的试件位移延性系数与实测值接近。计算极限位移总体小于实测极限位移，根据表3考虑安全系数的极限塑性转角也总体小于实测极限塑性转角。因此，在钢筋混凝土箱型墩延性抗震性能分析中，可以将极限位移和极限转角都作为延性抗震性能指标，与《公路桥梁抗震设计细则》［8］采用的延性性能指标一致。

表4 等效塑性铰长度lp的经验计算公式Tab.4 Empirical formula of equivalent plastic hinge length lp

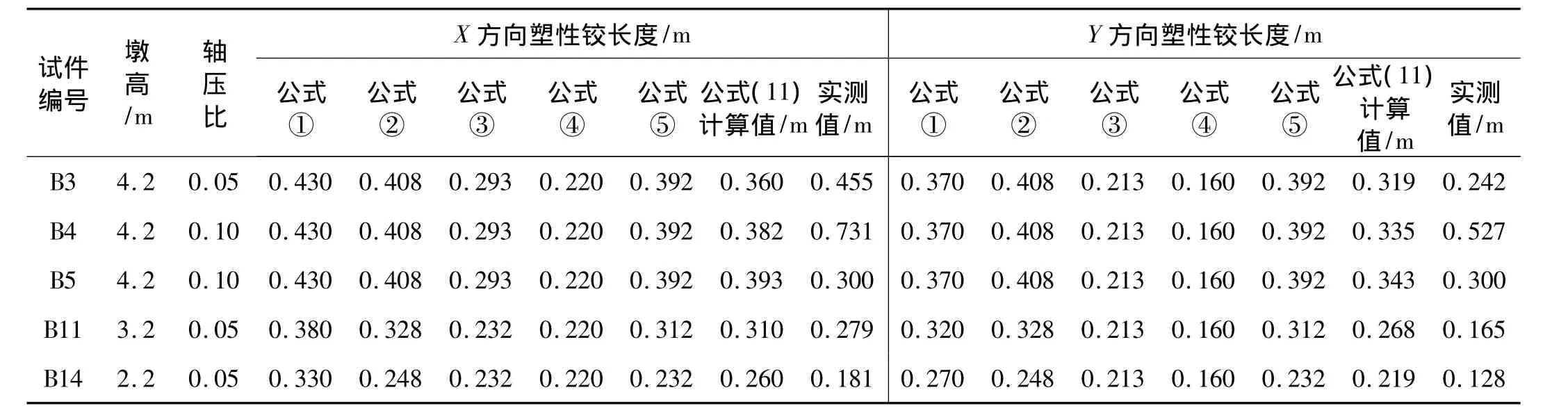
表5 实测和计算等效塑性铰长度比较Tab.5 Comparison of testing and calculating equivalent plastic hinge length

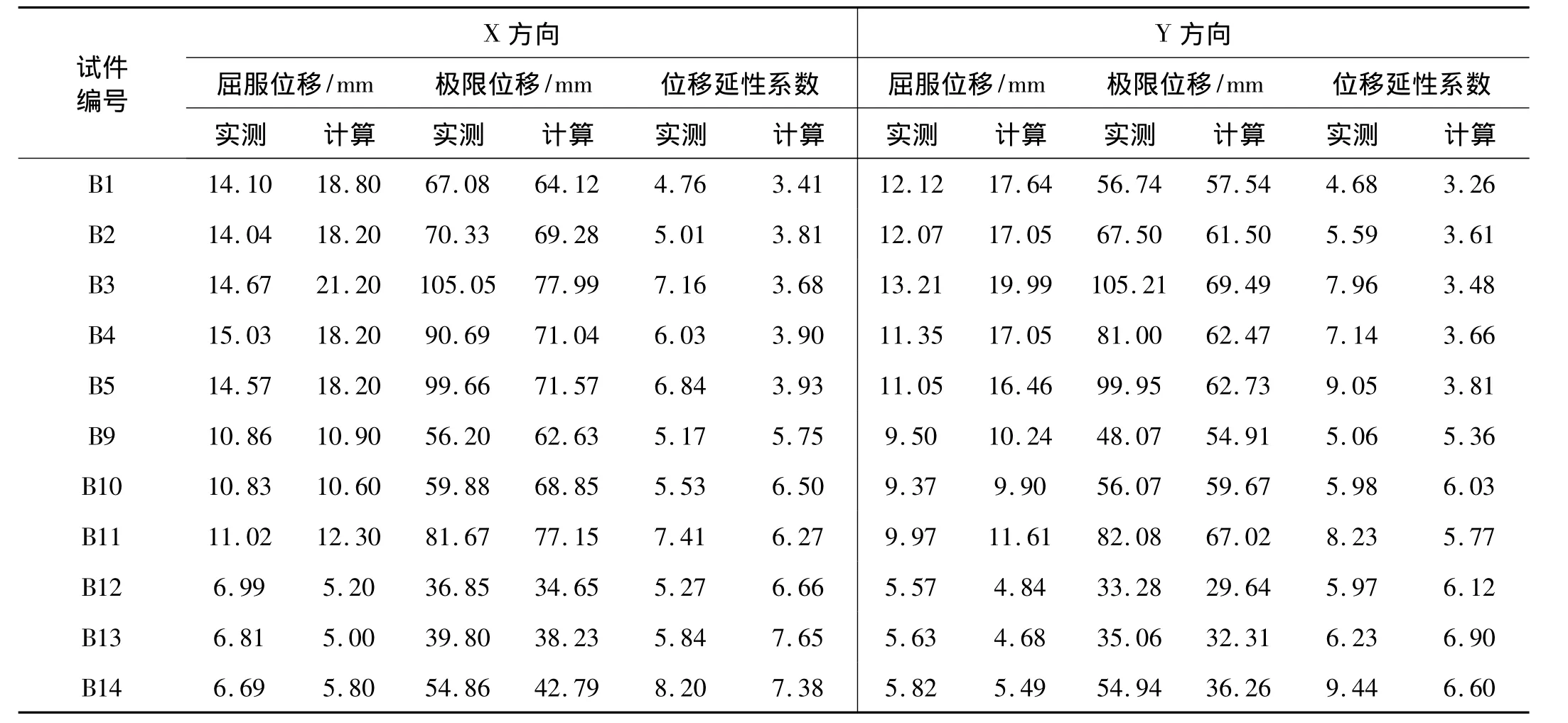
表6 实测与计算位移及位移延性系数比较Tab.6 Comparison of testing and calculating displacement and displacement ductility factor

4 结论

(1)根据钢筋混凝土箱型墩双向拟静力试验，轴压比越小，高宽比越大试件，变形能力越大。高宽比13.1的试件，配箍率越小，变形能力越大。

(2)模型墩实测最大弯矩基本大于计算最大弯矩，高宽比和轴压比越大的试件实测弯矩越大。试件截面实测极限曲率小于计算极限曲率，高宽比越大的试件实测极限曲率越小且极限曲率出现在变截面以上位置。说明高宽比越大的试件截面能够发挥的塑性转动能力越小。

(3)根据试验和计算结果，考虑双向荷载作用的钢筋混凝土箱型墩，计算极限塑性转角时，在高宽比大于2.5且小于等于10范围内，安全系数取值为K=4.0。在高宽比大于10小于13.1时，安全系数取值为K=7.0。

(4)根据钢筋混凝土箱型墩双向拟静力试验和箱型截面弯矩曲率分析，得到了其延性抗震性能计算分析的公式法。计算极限位移和极限塑性转角总体小于实测值，极限位移和极限塑性转角可以作为延性抗震指标，用于钢筋混凝土箱型墩延性抗震性能分析。

［1］Priestley M J N，Park R.Strength and ductility of concrete bridge columns under seismic loading［J］.ACI Structural Journal，1987，84(1):61 －67.

［2］ Watson S，Park R.Simulated seismic load tests on reinforced concrete columns［J］.Journal of Structural Engineering，ASCE，1994，120(6):1825－1849.

［3］ Code of Practice for the Design of Concrete Structures［S］.NZS 3101:1982.Wellington:Standards Association of New Zealand(NZS)，1982.

［4］日本道路协会.道路桥示方书.同解说，V耐震设计篇［M］.东京:日本道路协会，2002.

［5］ American Association of State Highway and Transportation Official.Guide Specifications for LRFD Seismic Bridge Design［S］.Washington，D.C.:American Association of State Highway and Transportation Officials，2007.

［6］杨新宝.钢筋混凝土桥梁抗震性能评估与加固［D］.上海:同济大学，1997.

［7］范立础，卓卫东.桥梁延性抗震设计［M］.北京:人民交通出版社，2001.

［8］JTG/T B02－01－2008.公路桥梁抗震设计细则［S］.

［9］宋晓东.桥梁高墩延性抗震性能的理论与试验研究［D］.上海:同济大学，2004.

［10］崔海琴，贺拴海，宋一凡.空心矩形薄壁墩延性抗震性能试验［J］.公路交通科技，2010，27(6):58－63.CUI Hai-qin，HE Shuan-hai，SONG Yi-fan.Experimental study on anti-seismic ductility of hollow rectangular thinwalled pier［J］.Journal of Highway and Transportation Research and Development，2010，27(6):58 －63.

［11］郝文秀，阎贵平，钟铁毅，等.反复荷载作用下活性粉末混凝土空心桥墩力学性能的试验研究［J］.铁道学报，2009，31(5):60－64.HAO Wen-xiu， YAN Gui-ping， ZHONG Tie-yi， et al.Experimental study on mechanical behavior of reactive powder concrete piers with hollow cross-sections subjected to cyclic loading［J］.Journal of The China Railway Society，2009，31(5):60－64.

［12］艾庆华，王东升，李宏男，等.基于塑性铰模型的钢筋混凝土桥墩地震损伤评价［J］.工程力学，2009，26(4):158－166.AI Qing-hua，WANG Dong-sheng，LI Hong-nan，et al.Seismic damage evaluation of RC bridge columns based on plastic hinge model［J］.Engineering Mechanics，2009，26(4):158－166.

［13］孙治国，郭 迅，王东升，等.钢筋混凝土空心墩延性变形能力分析［J］.铁道学报，2012，34(1):91－96.SUN Zhi-guo， GUO Xun， WANG Dong-sheng， et al.Analysis on ductile deformability of hollow reinforced concrete bridge piers［J］.Journal of The China Railway Society，2012，34(1):91－96.

［14］JGJ 101－96.建筑抗震试验规程［S］.JGJ 101－96.

［15］葛继平.节段拼装桥墩抗震性能试验研究与理论分析［D］.上海:同济大学，2008.

［16］朱伯龙.结构抗震试验［M］.北京:抗震出版社，1989.

［17］ Slivia M，Frank M，Michael H.Scott and Gregory L.Fenves.OpenSees Users Manual［S］.PEER，University of California，Berkeley，2004.

［18］ Kent D C，Park R.Flexural members with confined-concrete［J］.Journal of the Structural Division，1971，97(7):1969－1990.

［19］张继承，林振宇.低周反复荷载下异形钢管混凝土柱力学性能有限元分析［J］.武汉工程大学学报，2010，32(5):60－65.ZHANG Ji-chen，LIN Zhen-yu.Finite element analysis on mechanical properties of special-shaped concrete-filled steel tubular under low cyclic loading［J］.Journal of Wuhan Institute and Technology University，2010，32(5):60－65.

［20］ California Department of Transportation.CALTRANS Seismic Design Criteria［S］.V 1.3.USA，2004.