基于疏散效率分析的过道隔栏优化设置研究

□张兰香 刘梦婷 陈增强 郑小平 [北京化工大学 北京 100029]

引言

过道隔栏（Passageway railing）（见图1）设置于地铁站、航空楼等人群密集的场所，主要起到分流的作用。在大规模人群紧急疏散下，过道隔栏对于疏散效率有着重要的影响，其设置的长度对于疏散效率的影响值得专门研究。

图1 过道隔栏示意图

疏散效率不仅取决于疏散者的逃生行为[1]，还取决于疏散场景的空间结构[2,3]。过道隔栏的设置可视为出口前移，能够减轻疏散者在进入自动扶梯和楼梯系统前的区域可能存在的局部行人阻塞，对人流起到物理干预作用。目前只有少数相关性成果，且大部分是针对设施的分流作用进行研究的。Hughes认为通过设置障碍物减小了疏散人群的密度，从而减少疏散时间[4]。Kirchner,Nishinari &Schadschneider于2003年引入了摩擦系数刻画行为冲突，研究发现障碍物一方面迫使一些疏散者绕道而行，延长了其疏散时间；另一方面可以对疏散人群进行分流，减少冲突[5]。基于疏散者的自组织行为，Helbing等也认为障碍物的合理设置可以减少出口附近的堵塞，从而减少疏散时间并使人流趋于稳定；比如“之字形”障碍柱等[6]。之后，Zheng,Li &Guan专门研究了障碍墙，认为在一定范围内，改变障碍墙长度可以使疏散人群的分布更加均匀[7]。过道隔栏在实践中比比皆是，但其长度的设置缺乏科学依据。

本文研究将采用元胞自动机模型，根据疏散设施的特殊性对疏散者引入了不同行走速率；放弃静态场值原有的“距离”含义，以“时间长短”重新定义静态场值大小改进了地板场模型；然后通过仿真讨论不同参数对于人群疏散过程的影响，以提取过道隔栏长度与疏散效率的规律性认识。

一、模型

研究采用CA模型。将图1所示研究区域离散为二维元胞网格，每个元胞大小为0.5m×0.5m，其状态为空或被1人占据。疏散者的行动取决于：1）静态地板场值，即：当前疏散者到出口的时间；2）两类设施的吸引度。到出口的等待队列长度越短，吸引度越大。

（一）速度

将疏散空间划分走廊区、楼梯区和自动扶梯区，自动扶梯和楼梯长度相同，但自动扶梯以额定速率vrated运行。因此，各个区域疏散者的有效通行速率分别为：

走廊区（近邻且与自动扶梯和楼梯第一个台阶相接并无拐角的走廊）：

楼梯区：

自动扶梯区：

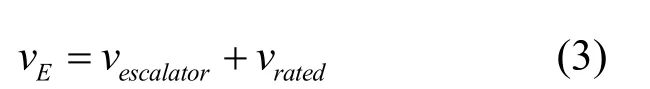
其中，vF、vS、vE分别表示疏散者在走廊区、楼梯区、自动扶梯区的有效通行速率，m/s；vfloor、vstair、vescalator分别表示疏散者在走廊、楼梯、自动扶梯的行走速率，m/s；vrated表示自动扶梯的额定速率，m/s；不同区域疏散者的速率影响每时步疏散者位置的更新概率[8]。疏散者的行走速率控制规则为：

1）如果疏散者位于通行速率最大的区域，则疏散者每时步移动一个元胞，时间步长为：

其中LΔ 表示元胞的大小；

2）如果疏散者位于通行速率较小的区域，则定义速率比：

其中X=｛vF,vS,vE｝，x表示X中不是最大的两个元素之一。此时的控制规则是：

a）对于疏散区域内的所有人生成一个[0,1]内的随机数；

b）对位于速率较小的两个区域的疏散者，若随机数小于等于xXη∈，则疏散者以xXη∈的概率移动以更新他们的位置，否则不动。

（二）静态地板场

通常意义下，静态场S表示场景内任一位置到出口处的最近距离，离出口越远，则静态场值越小。对疏散场景内的每个疏散者，向邻域内任一格子移动的概率p(m,n)由（5）式决定。其中，ks∈ [ 0,∞)为静态场参数，其强度表示疏散者对周围环境信息的了解程度。ks→0时，意味着静态场对疏散者不起任何指导作用，疏散者趋于随机行走。ks→∞时，疏散者能选择最短路径逃生。

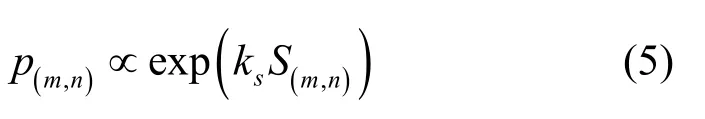
但是在地铁站的疏散中疏散者对路径的选择取决于最先离开自动扶梯或者楼梯顶端，因此，以疏散者离开自动扶梯或者楼梯顶端所需的最短时间T重新设计静态场S。假设疏散者每一时步移动一个元胞，进入到与之相邻且未被占据的八个或五个元胞之一（见图2），或保持不动，其下一时刻的位置由地板场决定。静态场值越小说明所用的时间越短。紧急疏散过程中，疏散人群将由高场值区域向低场值区域移动。

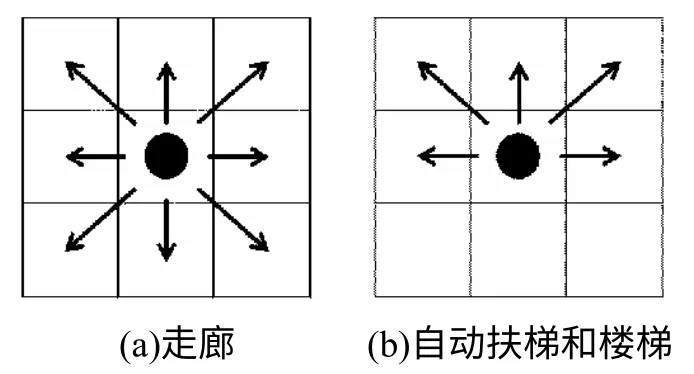
图2 疏散者可移动的方向

基于时间的静态场赋值规则为：

1）疏散空间被划分为(M,N)矩形元胞。

2）出口赋值为0，墙、扶手及过道隔栏区域赋予一个较大的值，以保证疏散者不会选择这些元胞。

3）从出口往下依次进行地板场的赋值。对于非出口的任意元胞(m,n)，其静态场值Tm,n的计算公式如下：

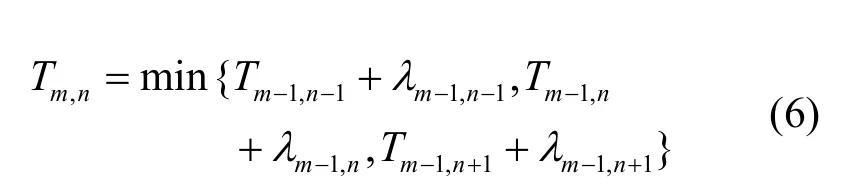
其中，Tm,n表示元胞(m,n)的静态场值，分别表示从当前元胞(m,n)到元胞(m-1,n-1),(m-1,n),(m-1,n+ 1)的时间，其值为：

对楼梯区、自动扶梯区和走廊区，上式中v分 别取值为vS、vE和vF。

4）重复步骤3）直到疏散区域中所有元胞都被赋值为止。

此时，对疏散场景内的每个疏散者，向邻域内任一格子移动的概率p(m,n)由（8）式决定。

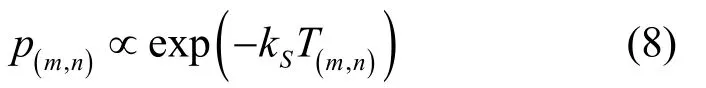
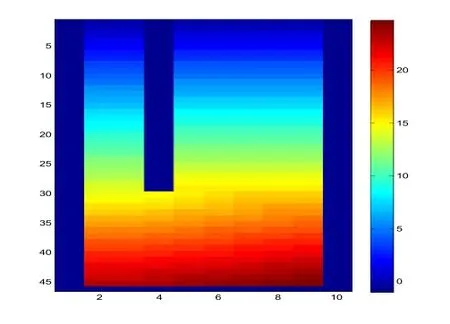
图3 44*8个元胞的疏散场景静态地板场赋值图的二维表示

疏散者在疏散过程中根据地板场值选择进入其邻域的元胞空间，当存在多个疏散者争抢一个元胞时，引入摩擦系数μ[9]表示疏散者彼此相互阻碍使对方不能到达目标位置的程度。冲突中的所有人以概率μ待在原来的位置，系统会以1-μ的概率选择其中之一移向目标位置。

（三）出口选择

过道隔栏的设置相当于将最终出口（Final Exit）前移（见图4中E和S两个出口）。若过道隔栏长度为L米，则疏散者在过道隔栏以下区域需做出两个出口的选择，且最晚的决策位置是L+0.5米，即近邻过道隔栏下边缘的位置。选择方法如下：

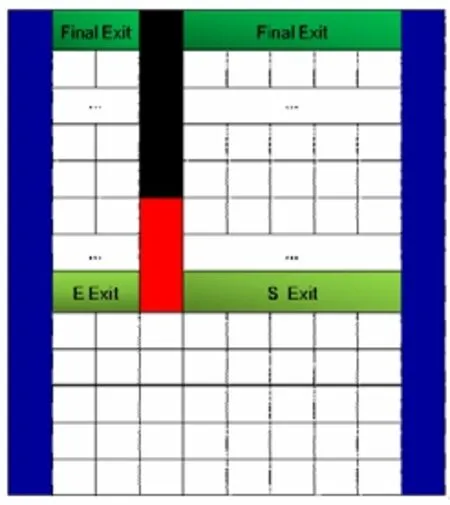
图4 出口选择

1．用Zheng 等[7]提到的方法结合前面确定两个子出口对应的地板场E（)和地板场S（)，当处于位置(m,n)的疏散者选定其中一个出口后，则可通过相应的地板场更新位置。

2．影响疏散者选择出口的因素有：疏散者到备选出口的用时Tik(m,n)和备选出口前等候排队的队列长度(m,n)。参考Alizadeh[10]提出的方法，Wik(m,n)表示第i时步元胞(m,n)关于出口k（k=E或k=S）的权重值。将以上两个因素分为两类，则有：

其中：Tik(m,n)表示第i时步元胞(m,n)到出口k需要的时间也即静态场值；(m,n) 表示第i时步与元胞(m,n)相比离出口较近的人数，其表达式如下所示：

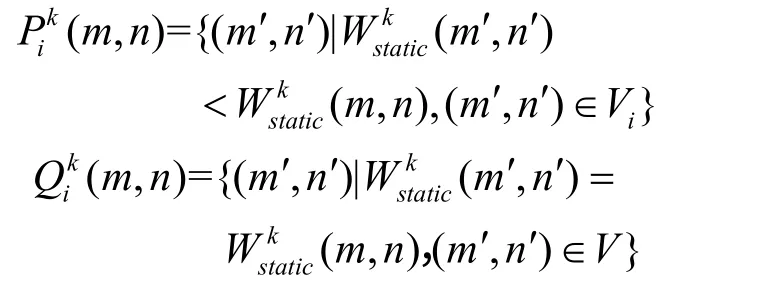
3．对疏散场景内的每个疏散者，元胞（m,n）上的疏散者选择出口k的概率为：

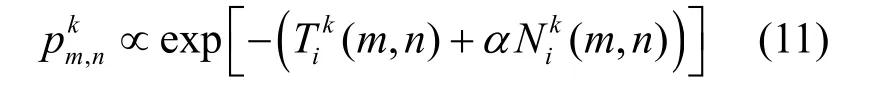
其中α为人群避让系数。α值越大，的作用越大，表明疏散者越想避开人群，选择人少的出口。特别的，当对于α=0时，即疏散者只考虑逃生时间，疏散者只按照静态场选择出口。

二、仿真

结合真实疏散场景及《地铁设计规范》（GB 50157-2003）的相关规定，本文疏散场景如图1所示。其中，自动扶梯有效宽度为1米，倾斜角为30°；楼梯有效宽度为2.5米；两种设施长度为12米。根据《自动扶梯和自动人行道的制造与安装安全规范》（GB 16899-2011），常见的自动扶梯运行速率有：0.5m/s、0.65m/s、0.75m/s。高峰时期地铁站内疏散者人群组成部分主要是中青年，所以疏散者在两种疏散设施上的速率由对Fruin[11]及Kinsey[12]的结果取均值得到。具体数值见表1。

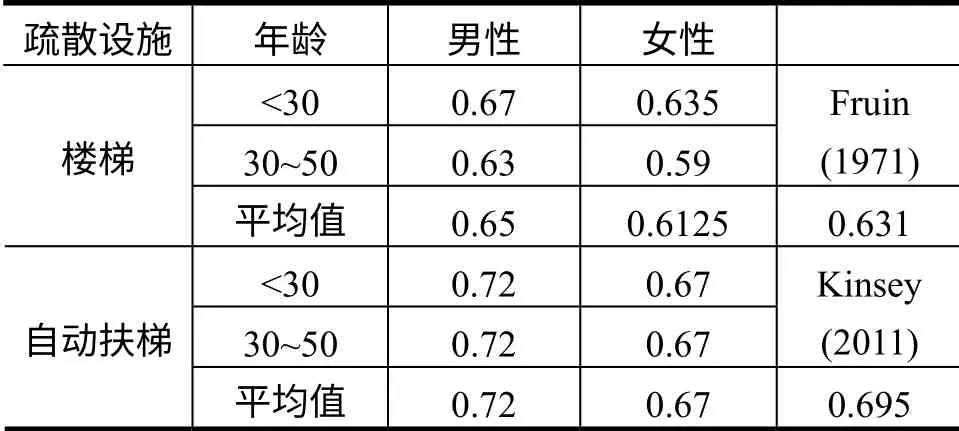
表1 疏散者在自动扶梯、楼梯上的行走速率

在自动扶梯和楼梯前面的走廊是地铁内疏散的瓶颈区域，对该区域疏散者的速率现在还没有确定的研究成果，结合实际文中取值为0.59 m/s[13]。大部分乘客均能分辨出地铁站出口位置，所有对路径信息的掌握很充分，设Ks=10。

（一）人群避让系数α

动态出口选择中的参数α表示的是人群避让系数。下面将研究其对疏散者出口选择及疏散效率的影响。

当α从0到1变化时，选择楼梯逃生的人流占总流率的比率有很大差异。当α=0时，疏散者只根据两出口对应的静态地板场选择出口，原则上疏散者应选择所用逃生时间少的自动扶梯，但自动扶梯的有效承载宽度有限，致使自动扶梯前出现疏散者排队现象，仍有约51%的疏散者选择楼梯（fsta/f=0.51）。当α∈[0,0.4]时，fsta/f值迅速增大。说明考虑到出口附近人群分布以后选择楼梯的人增多。

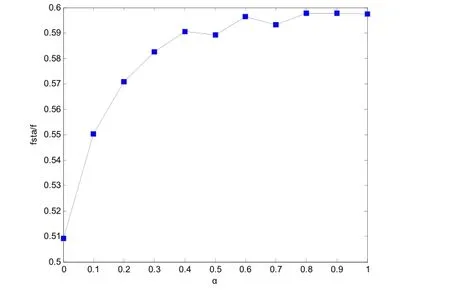
图5 考虑避让人群并选择楼梯的疏散者流率 与总流率比值和人群避让系数α关系图

当α∈[0.4,0.8]时，可以看多fsta/f值有小幅度上下波动。这是因为疏散者同时考虑逃生时间和两种设施前人群分布两个因素时出现的犹豫不决、徘徊不定所造成的。当α＞0.8时，fsta/f值均保持为一个常数。此时疏散者选择逃生路径考虑尽可能避开拥堵人群，在两种设施前面排队情况呈现出动态均衡。选择楼梯的疏散者的比例近似为60%左右。

突发事件发生时，自动扶梯、楼梯两种疏散设施前发生拥堵时一般会有53%左右的疏散者根据拥堵情况选择楼梯[14]。但是在上下班高峰期，疏散者没有恐慌等心理，考虑两种设施前拥堵发生的概率会比突发事件下的更高一点。从图5也可以看到，当α=0.2时，选择楼梯的疏散者约为57%。所以为了更接近于现实情况，在下面的仿真中，选取α=0.2作为人群避让系数。

（二）摩擦系数μ与使流率最大的过道隔栏长度值的关系

由上图可以看到，在初始密度为1.5人/m2，自动扶梯运行速率为0.65m/s，走廊长度为0到5米长的情况下，使得疏散效率最大的过道隔栏最优值的范围在2到5米之间，也即：Lopt为走廊长度的40%到100%之间。μ＜0.6时，使流率最大的过道隔栏最优值介于2到3米之间，此时过道隔栏的长度宜设置3米（60%*Lf）；0.7μ≥ 时过道隔栏最优值为5米（100%*Lf），也即：过道隔栏设置长度应为走廊长度。运动人群在走廊区被物理分割成两股人流，疏散者不能按照子出口前的人群分布改变选择，其自身所处的位置已经决定了他们进入对应的设施走廊。因此减少因争抢所偏好的设施而产生的冲突，不但有利于疏散效率，对疏散安全性的提高也有很大作用。

由于现实场景中μ的具体数值无法测算，在自动扶梯运行速率为0.65m/s的情况下，应对日常所需，地铁站中过道隔栏的长度宜为走廊长度的60%，但是在突发事件或者人员恐慌的情形下过道隔栏长度宜为走廊长度。由于μ=0,0.3,0.7能够代表摩擦参数对Lopt的影响趋势，之后的仿真就这三个值分析不同的自动扶梯运行速率下过道隔栏长度对流率的影响。

（三）动扶梯运行速率为0.5、0.65和0.75m/s时过道隔栏长度对流率的影响

图7是人群密度为1.5人/m2、走廊长度为5米、自动扶梯运行速率从0.5到0.75m/s变化时过道隔栏长度L与流率变化图。如图7所示，疏散者之间不存在冲突（μ=0）时，随着过道隔栏长度L的增大，疏散流率呈先增后减小的趋势，使得流率最大的过道隔栏长度Lopt∈[2.5,3]；存在一定的冲突（如μ=0.3）时，随着L的增大，疏散流率的变化趋势同样先增大后减小，使得流率最大的隔栏长度为Lopt=3，且不受自动扶梯速率的影响；但如果冲突程度高（如μ=0.7），随着过道隔栏长度L的增加，不同过道隔栏长度下疏散者流率波动较大，此时过道隔栏长度的最优值Lopt∈[3,5]，也即：过道隔栏的最优值占到走廊长度的60%～100%。

对比三种自动扶梯运行速率下的曲线，自动扶梯的运行速率越大则流率越大。对于无竞争和竞争强度较高的人群改变隔栏长度是有效的。主要是因为争抢行为在一定程度上阻碍行人的运动，包括行人由于出口重新选择产生的徘徊运动。因此，当自动扶梯运行速率较高时，通行能力较高，争抢行为是效率低下的主要原因，改变过道隔栏长度影响较小，而当自动扶梯运行速率较低时，过道隔栏更多在于分散了子出口前的拥堵而有所作用。

图7 自动扶梯运行速率从0.5到0.75变化时 过道隔栏长度L与流率变化图（ρ=2.5人m2,Lf=5米）

（四）不同人群密度下过道隔栏长度对流率的影响

下面将在相同场景下讨论不同人群密度下过道隔栏的设置对疏散的影响。

图8 不同人群密度ρ（人/m2）下自动扶梯和楼梯流率值 比率随过道隔栏长度L变化图

图8是人群密度为分别为1、1.5、2、2.5人/m2、走廊长度为5米、自动扶梯运行速率vrated=0.65m/s时过道隔栏长度与自动扶梯与楼梯流率比率变化图。自动扶梯与楼梯流率比率值越接近1，说明两种设施的通行能力上的差异越小。如图8(a)、(b)所示，当疏散者之间不存在冲突（μ=0）和存在一定冲突（如μ=0.3）时，对于人群密度ρ＜2的情况，随着过道隔栏长度的增大，自动扶梯与楼梯流率比率存在不同程度的下降，密度越小该比率下降的越快。但是，对 2ρ≥ 的情况，自动扶梯前的排队队列促使部分疏散者重新选择楼梯。因此过道隔栏的设置对两种设施的通行能力几乎不产生影响，单位宽度的自动扶梯通行能力是楼梯的1.4倍左右。

如图8（c）所示，当疏散者之间冲突（如μ=0.7）很高时，对ρ=1的情况，随着过道隔栏长度的增大，自动扶梯与楼梯流率比率快速下降。但是对ρ＞1的情况，随着过道隔栏长度的增大，该比率只有小幅波动，比率值约在1.05左右，说明过道隔栏的设置对两种设施的通行能力影响很小且此时单位时间、单位宽度上两种设施上通过的人数几近相等。原因：人群密度高且疏散者之间有较高程度的冲突时，疏散者的争抢行为也较明显。这种争抢行为在一定程度上阻碍行人的运动，尤其是在偏好设施前表现的尤为突出。为了避免不必要的摩擦以节省疏散时间，部分疏散者会放弃偏好设施转而选择楼梯，故而两种设施的通行能力几近相等。同样，流率比率的波动可能是由于疏散者在出口选择时出现的犹豫徘徊行为所引起的。

三、结论

本文采用CA模型，研究了地铁站自动扶梯和楼梯之间过道隔栏（图1所示）对疏散效率的影响。考虑到自动扶梯和楼梯两种疏散路径的不同，本文对地板场模型进行了改进，用“时间”代替了原有的“距离”的含义；并引入了疏散者多速度的更新规则。通过对人群疏散过程的仿真和分析，得出以下结论：

1．过道隔栏并不总是阻碍疏散者的通行，在一定条件下能够提高效率和疏散安全性。

2．随着疏散者之间争抢程度的增大，Lopt在走廊长度的60%到100%之间变化。应对日常所需，地铁站中过道隔栏的长度宜为走廊长度的60%，但是在突发事件或者人员恐慌的情形下过道隔栏长度宜为走廊长度。

3．自动扶梯运行速率越大，改变过道隔栏长度对流率的影响程度越大。自动扶梯运行速率越慢，或疏散群体间的冲突程度较高，过道隔栏的长度应设置相对较长。

4．过道隔栏的设置对自动扶梯和楼梯两种疏散设施的通行能力起到明显的均衡作用。合理设置过道隔栏不但可以提高疏散效率，而且可以减少疏散者在偏好设施前的争抢行为，减少疏散安全隐患。

[1]HELBING D,FARKAS I,VICSEK T.Simulating dynamical features of escape panic[J].Nature,2000,407(6803):487-490.

[2]ZHAO D,YANG L,LI J.Exit dynamics of occupant evacuation in an emergency[J].Physica A:Statistical Mechanics and its Applications,2006,363(2):501-511.

[3]LIU S,YANG L,FANG T,et al.Evacuation from a classroom considering the occupant density around exits[J].Physica A:Statistical Mechanics and its Applications,2009,388(9):1921-1928.

[4]HUGES R L.The flow of human crowds[J].Annual review of fluid mechanics,2003,35(1):169-182.

[5]KIRCHNER A,NISHINARI K,SCHADSCHNEIDER A.Friction effects and clogging in a cellular automaton model for pedestrian dynamics[J].Physical review E,2003,67(5):56-122.

[6]HELBING D,BUZNA L,JOHANSSON A,et al.Self-organized pedestrian crowd dynamics:experiments,simulations,and design solutions[J].Transportation science,2005,39(1):1-24.

[7]ZHENG X,LI W,GUAN C.Simulation of evacuation processes in a square with a partition wall using a cellular automaton model for pedestrian dynamics[J].Physica A:Statistical Mechanics and its Applications,2010,389(11):2177-2188.

[8]YUAN W,TAN K.A novel algorithm of simulating multi-velocity evacuation based on cellular automata modeling and tenability condition[J].Physica A:Statistical Mechanics and its Applications,2007,379(1):250-262.

[9]KIRCHNER A,KLUPFEL H,NISHINARI K,et al.Simulation of competitive egress behavior:comparison with aircraft evacuation data[J].Physica A:Statistical Mechanics and its Applications,2003,324(3):689-697.

[10]ALIZADEH R.A dynamic cellular automaton model for evacuation process with obstacles[J].Safety Science,2011,49(2):315-323.

[11]FRUIN J J.Pedestrian Planning and Design[M].New York:Metropolitan Association of Urban Designers and Environmental Planners.Inc.,1971.

[12]KINSEY M J.Vertical transport evacuation modeling[D].London:University of Greenwich,2011.

[13]杨涵,伍梦欢,张含笑,等.地铁换乘站不同设施区域乘客走行速度分析[J].交通运输系统工程与信息,2011,11(A01):140-145.

[15]何理,钟茂华,史聪灵,等.地铁突发事件下乘客疏散行为调查研究[J].中国安全生产科学技术,2009,5(1):53-58.