桥梁半平行钢丝索对称断丝的力学特性分析
2013-05-10彭崇梅张启伟李元兵
彭崇梅,张启伟,李元兵
(1.同济大学 土木工程防灾国家重点实验室,上海 200092;2.同济大学 桥梁工程系,上海 200092)
桥梁工程中,拉索或吊杆应用广泛,由于施工或使用过程中的磨损、老化、腐蚀、断丝等原因,相当一部分拉索或吊杆在成桥后不久便出现严重损伤,甚至导致桥梁坍塌.高强钢丝或钢绞线断丝是拉索损伤的重要形式之一,断丝后索体内各钢丝会发生内力重分布,不仅降低钢丝索承载力,而且在腐蚀及车辆、温度等外荷载作用下,截面内其他钢丝进一步断裂,直至拉索(吊杆)丧失承载力.研究表明,断丝和接触变形是引起拉索截面钢丝内力重分布的主要影响因素.
目前,半平行钢丝索是桥梁工程中拉索的主要应用形式,而这方面的研究主要为基于平行直钢丝假定的并联模型或钢绞线模型.针对半平行钢丝索特殊的构造,其适用性应作进一步探讨,且这些模型不能同时考虑接触变形和断丝的影响.接触变形的影响方面,Raoof和 Hobbs[1]在其半连续模型中考虑了接触应力对变形的影响;LeClair[2]的研究表明,对于给定的钢绞线应变,钢丝间的接触变形减少了单位长度上钢丝间的平衡接触力和钢丝拉力;Nawrocki[3]等通过建立不同股和丝的有限元模型,分析了钢丝的接触应力和弹性变形;Jiang[4-5]等通过考虑钢丝间局部接触、摩擦、塑性变形,建立了轴向荷载作用下的有限元模型;Seyed等[6]建立了考虑径向接触的简单直钢绞线有限元模型,并与相关文献中的试验数据进行了对比.以上研究对象均是完好钢绞线(钢丝绳).断丝模型的研究方面,Cappa[7]通过测试外层单根断丝的7丝钢绞线,研究了断丝后钢绞线中钢丝拉力分布规律;Chein和Costello[8],MacDougall[9]从不同角度研究了7丝钢绞线断丝后的钢丝拉力分布和断丝影响长度;Raoof[10]基于半连续模型,研究了外层单根钢丝断裂后,钢绞线(钢丝绳)中钢丝拉力分布规律和断丝影响长度;李元兵[11]在 MacDougall[9]的基础上,应用有限元方法研究了断丝后钢绞线吊杆截面内钢丝内力分布及护套握裹力、钢丝间摩擦系数等对吊杆内钢丝拉力分布的影响.
综上所述,已有研究对象主要为钢绞线(钢丝绳),未同时考虑断丝和接触变形的影响,且用以描述钢丝间接触、摩擦和滑移的物理量也很难通过试验方法获得,从而难以准确描述多层半平行钢丝索的受力行为.本文基于Love[12]曲杆理论,忽略钢丝弯矩、扭矩和剪力,考虑泊松效应、接触变形以及钢丝间的接触力和摩擦力的影响,推导了静力拉伸荷载作用下多层半平行钢丝索的对称断丝模型,并通过数值计算重点讨论了拉索截面钢丝拉力分布规律、钢丝拉力增长系数和拉索轴向刚度及其影响因素.
1 模型推导及求解
1.1 对称断丝模型
基于半平行钢丝索的对称断丝模型,是将多层半平行拉索按钢丝螺旋半径进行分层,以单根钢丝为曲杆,忽略钢丝弯矩、扭矩和剪力,考虑泊松效应和钢丝间的接触、摩擦,基于Love[12]曲杆理论推导而得,但该模型未考虑钢丝间的接触变形,钢丝间的拉力分布差异难以体现.本文在该模型[13]的基础上,考虑了钢丝间接触变形的影响,对模型进行了进一步的修正,主要推导方程如下:
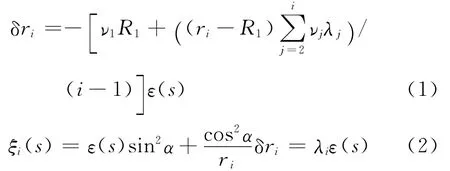
式(1),(2)中:δri为螺旋半径的变分,ri为第i根钢丝螺旋半径;R1为中心钢丝半径;νj为第j根钢丝泊松比;λj为应变系数;ε(s)为中心钢丝轴向应变;ξi(s)为外层未断钢丝的轴向应变;α为外层钢丝螺旋角.
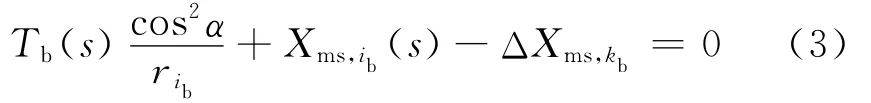
式中:Tb(s)表示断丝拉力;ib为断丝所在钢丝层;kb为断丝所在钢丝环;Xms,i表示第i层断丝径向接触力;ΔXms,k为第k+1环钢丝作用于第k环钢丝的接触力.

式中:Fu(s)为未断钢丝总拉力;E为钢丝弹性模量;Ac为中心钢丝面积;A0为外层钢丝面积;mi为第i层钢丝数目;λi表示螺旋钢丝应变系数;nb为断丝数目;Ku为未断钢丝总拉力系数.

式中:Tu,i(s)为未断钢丝拉力;Fb为断丝拉索总轴向力.
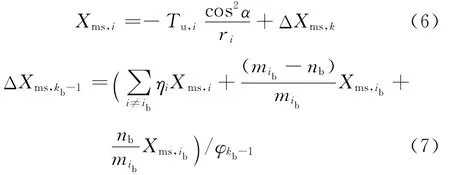
式中:ηi和φkb-1为权系数,与kb有关.
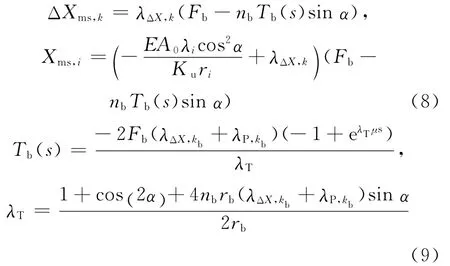
式(8),(9)中:λΔX,k和λP,k分别为 ΔXms,k和Pms,k提取公因式(Fb-nbTib(s)sinα)后的系数;μ为内部钢丝间摩擦系数.
影响长度La为
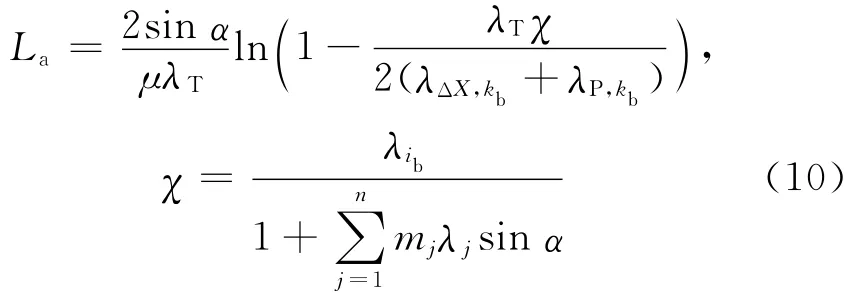
当La>L(拉索长度),索力剩余系数γ为
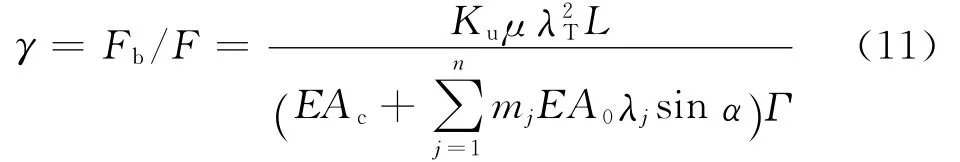
式中:F为完好拉索总轴向力;Γ的表达式参考文献[13].
当La<L,索力剩余系数γ为
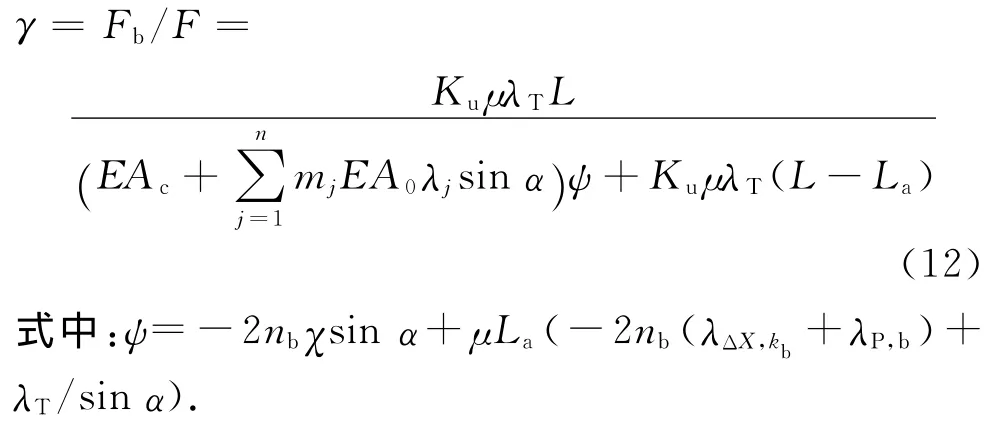
为研究接触变形对对称断丝模型钢丝拉力分布的影响,考虑泊松效应和径向接触变形的影响,则螺旋半径的变分式(1)可表示为

[14],两根相互线接触的平行圆杆之间的接触变形为
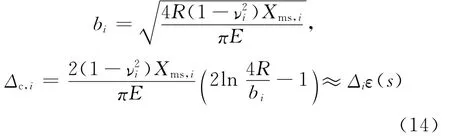
式(13),(14)中:Δdiag,j为第j环对角线钢丝与第j-1环对角线钢丝间的接触变形系数;Δc,i表示第i层钢丝的接触变形;Δi表示第i层钢丝的接触变形系数;R为外层钢丝半径.
由式(13),(14)可以看出,接触变形与钢丝间的接触力有关,而接触力又与断丝拉力Tb(s)有关,故螺旋半径的变分应是断丝拉力的函数,式(9)中各项系数亦是断丝轴向拉力的函数,且式(3)无法直接求出解析解,如此,将大大加大求解难度.为简化求解过程,同时又能定性地讨论接触变形对断丝模型预测结果的影响,将通过如下过程进行简化:首先,求出钢丝间的径向接触力(不考虑接触变形),再将径向接触力代入式(14),求出钢丝间的接触变形,后续计算中,将此接触变形作为不变量代入式(13),并和式(2)迭代求解,得到考虑接触变形的螺旋半径的变分,其余求解过程同不考虑接触变形的情况.
1.2 方程的求解
对于给定的半平行钢丝索,首先,不考虑接触变形,按前述断丝模型得到钢丝间的接触力,再将径向接触力代入式(14),求出钢丝间的接触变形,后续计算中,将此接触变形作为不变量代入式(13),并和式(2)迭代求解,得到考虑接触变形的螺旋半径的变分δri和外层钢丝应变系数λi;将计算得到的λi代入式(4),得未断钢丝总拉力系数Ku,代入式(5)、式(6),得外层未断钢丝拉力Tu,i和接触力Xms,i,对于给定的坐标s,假定Tb(s),代入式(3),(7),(8),可得ΔXms,kb,将ΔXms,kb代入式(9),可得新一轮的Tb(s)和接触力ΔXms,kb,如此循环,直到前后两轮计算得到的ΔXms,kb差值小于给定误差;再进入下一坐标s+Δs的计算,重复以上过程,直到拉索全长计算完为止.将上述计算结果代入式(10),可得影响长度La,代入(11)或式(12),可得索力剩余系数γ.全部计算过程可通过编程实现.
2 数值分析与讨论
为讨论接触变形对多层半平行钢丝索断丝模型的影响,参考桥梁工程中半平行钢丝缆索构造的技术参数,如无特别说明,均以Ф5-127的半平行钢丝索为例进行讨论.索长L取6m,钢丝直径为5mm,钢丝弹性模量E取197.9GPa,泊松比ν取0.3,内部钢丝间摩擦系数μ取0.12,护套握裹力Ws取2.0×10-6N·mm-1;钢丝总层数n为15,断丝所在钢丝层为第7层,断丝数为8根,所有断丝断口均位于L/2截面处.
2.1 索内钢丝拉力分布
为讨论接触变形对索内钢丝拉力分布的影响,考虑接触变形,对应的拉索钢丝拉力分布如图1、图2所示.其中图1和图2分别对应螺旋角为80°和86°时的钢丝拉力分布.图中“x=0”和“x=La/2”分别对应断丝处截面和影响长度处截面,图例中的序数表示未断钢丝所在的钢丝层.
由图1、图2可以看出,对称断丝情况下钢丝拉力分布规律如下:
(1)从图1a和图2a可以看出,钢丝拉力沿拉索纵向分布规律与不考虑接触变形相似,考虑接触变形时,断丝拉力随到断裂处距离的增加近似线性增加,断丝拉力变化明显;而未断钢丝拉力随到断裂处距离的增加近似线性衰减,在断裂处最大,如螺旋角为80°和 86°时,分 别 对 应Ti/Fb为 0.86% 和0.84%;影响长度内,各未断钢丝拉力增大,影响长度外,索体内同层钢丝拉力相等.但当螺旋角为80°时,各层未断钢丝间拉力分布不重合.
(2)从图1b和图2b可以看出,当螺旋角为80°时,考虑接触变形,拉索截面各层未断钢丝拉力不重合,钢丝拉力明显分布不均,钢丝间拉力差异在断丝处比影响长度外明显,如断丝处第6环和第4环Ti/Fb分别为0.86%和0.85%,影响长度外第6环和第4环分别为0.81%和0.80%,钢丝越往外环,拉力越大;当螺旋角为86°时,考虑接触变形,拉索截面各层未断钢丝拉力基本重合,如断丝处Ti/Fb均为0.84%,影响长度外均为0.80%,说明各层未断钢丝拉力分布较均匀.而不考虑接触变形时,拉索截面中钢丝拉力分布均匀,与螺旋角无关.
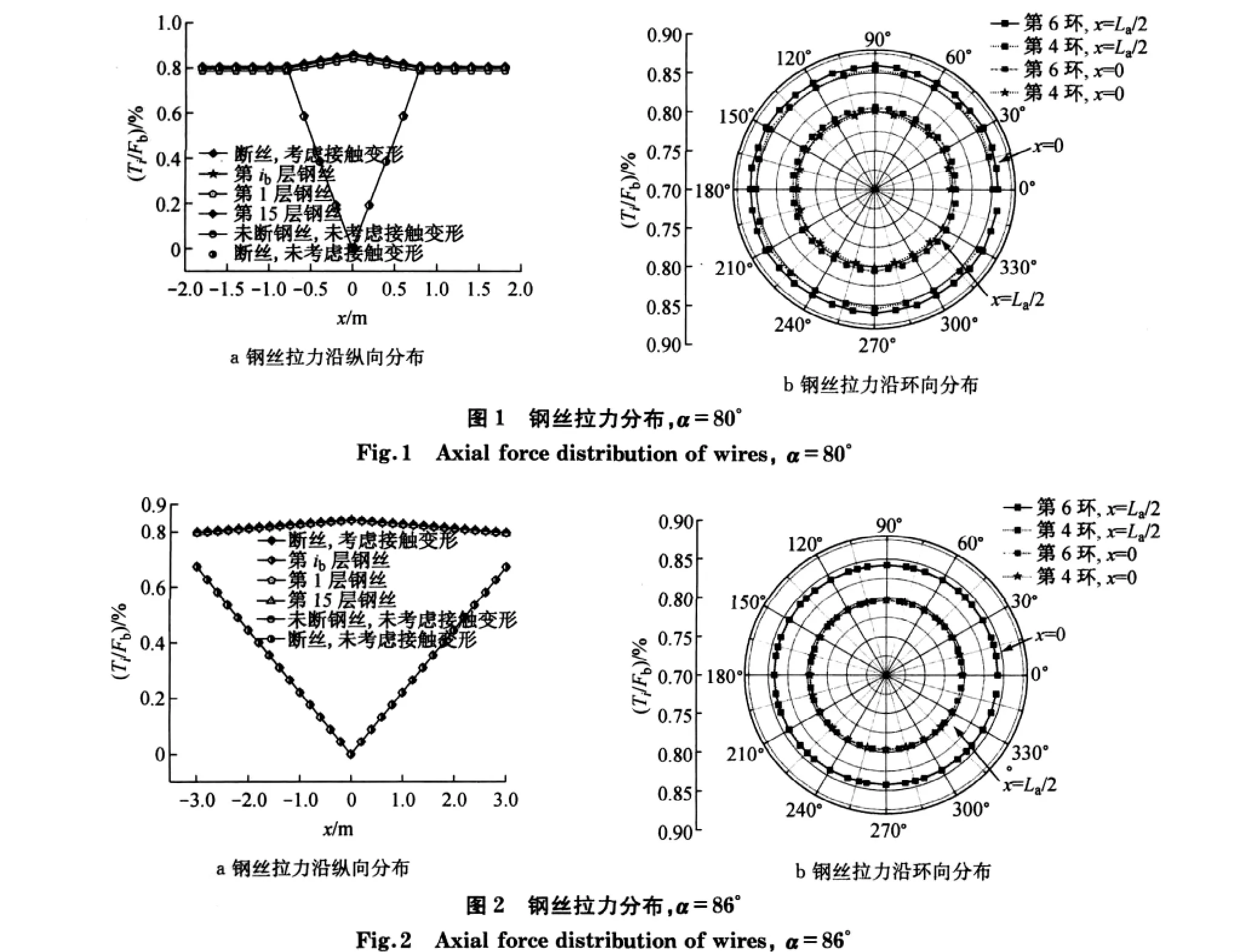
2.2 影响长度和索力剩余系数
为讨论接触变形对断丝影响长度和索力剩余系数的影响,考虑接触变形,对应的拉索断丝影响长度和索力剩余系数和螺旋角的关系曲线分别如图3、图4所示.
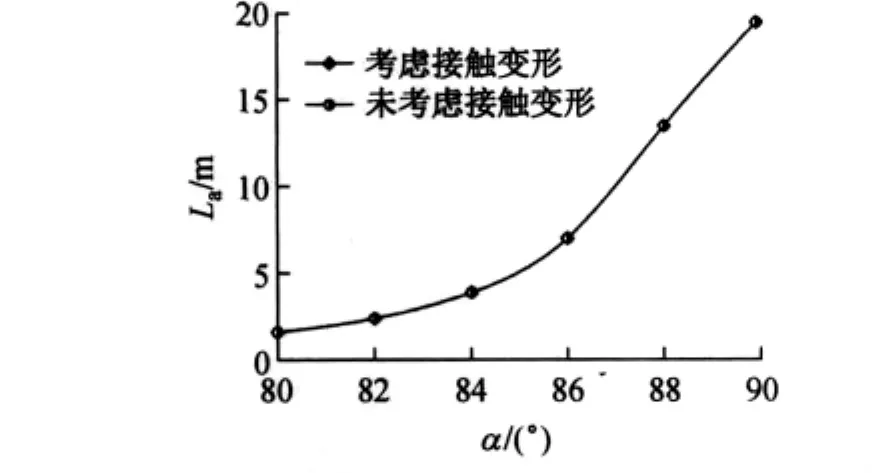
图3 影响长度随螺旋角变化关系曲线Fig.3 The affected length as a function ofα
由图3、图4可以看出,影响长度和索力剩余系数随螺旋角变化的规律如下:
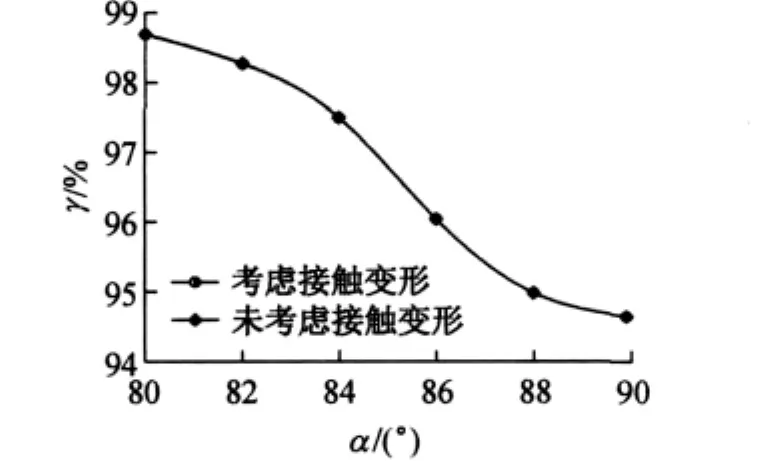
图4 索力剩余系数随螺旋角变化关系曲线Fig.4 Remaining prestress fraction as a function ofα
与不考虑接触变形相似,考虑接触变形时,随螺旋角的增加,断丝影响长度逐渐增加,而索力剩余系数则逐渐变小,拉索拉力损失率均小于拉索横截面损失率.不论考虑接触变形与否,图中影响长度和索力剩余系数随螺旋角的变化曲线基本重合,曲线间的差异可以忽略,说明接触变形对影响长度和索力剩余系数的影响不大.
3 钢丝拉力增长系数
工程实践中,主要应用基于平行直钢丝假定的并联模型计算半平行钢丝索,计算时假定截面内各钢丝拉力相等.这一模型忽略了外层钢丝的螺旋特性,且钢丝间的接触与摩擦也无法考虑,为研究半平行钢丝索中实际钢丝拉力分布和拉索中钢丝拉力增长幅度,将拉索截面内各根钢丝拉力相对于并联模型得到的钢丝拉力的比值定义为钢丝拉力增长系数λwi,有
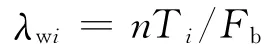
由2.1节可知,考虑接触变形,钢丝间的拉力分布不均匀,而不考虑接触变形拉力分布均匀,所以主要讨论考虑接触变形时钢丝间的拉力分布规律.考虑接触变形时,拉索截面钢丝拉力增长系数分布如图5、图6所示.
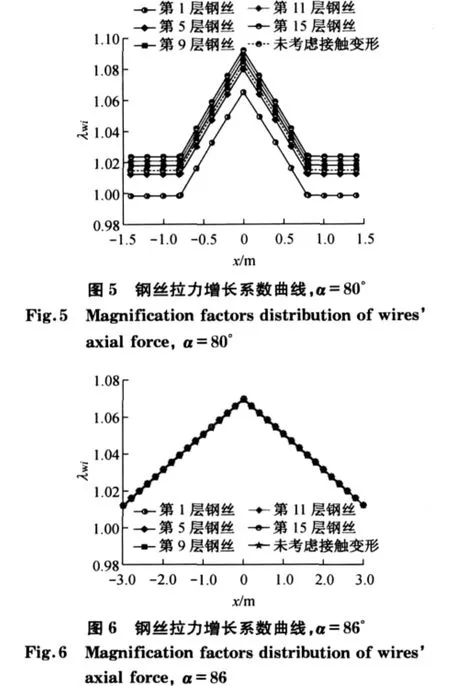
由图5、图6可以看出,钢丝拉力增长系数分布规律为:当螺旋角为80°时,影响长度内,钢丝拉力增长系数随到断裂处距离的增加呈线性衰减,在断丝处不均匀分布最明显,如最外层和最内层钢丝拉力增长系数分别为1.092和1.065;影响长度外,拉力增长系数保持不变,钢丝间拉力分布保持不变,如最外层和最内层钢丝拉力增长系数分别保持在1.024和0.998.螺旋角为86°,各层钢丝间拉力增长系数曲线基本重合,钢丝间的拉力分布较均匀.当螺旋角为80°和86°时,考虑接触变形时,拉索内最大钢丝拉力增长系数分别为1.092和1.070,未考虑接触变形时,最大钢丝拉力增长系数分别为1.083和1.069,增幅分别为10.84%和1.45%.
拉索中最大钢丝拉力增长系数和钢丝间的拉力分布不均匀程度可通过最大、最小拉力增长系数随拉索轴向坐标的变化曲线进行描述,如图7所示,拉索中最大、最小拉力增长系数随螺旋角的变化关系如图8所示.
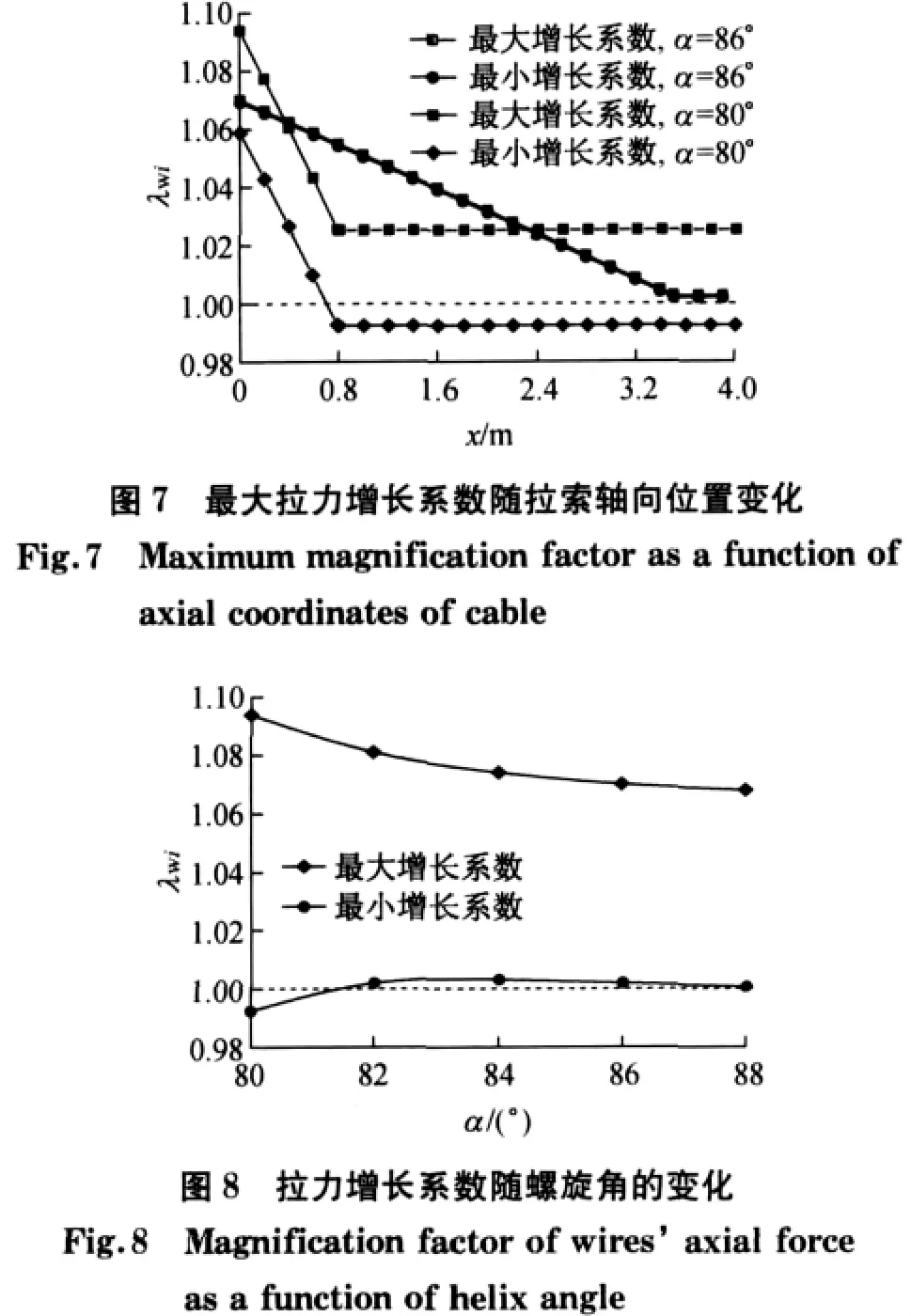
由图7可以看出,距离断丝处越远,截面最大、最小拉力增长系数越小,影响长度外,曲线变为水平,两项系数保持不变;当螺旋角为86°时,两曲线在拉索长度内基本重合,表示最大和最小增长系数间的范围很小,截面内钢丝拉力分布基本均匀;当螺旋角为80°时,两曲线间的差异较大,断丝处,最大、最小拉力增长系数为1.094和1.059,变化区间为0.035,影响长度外,两项系数分别变为1.025和0.992,变化区间为0.033,最大和最小拉力增长系数间变化区间较大,截面内钢丝拉力分布不均匀.由图8可以看出,随着螺旋角的增大,最大拉力增长系数逐渐变小(1.094~1.068),而最小拉力增长系数则逐渐增大(0.992~1.001),两者间的区间长度变短,即索体内钢丝间的拉力分布逐渐趋于均匀.
4 拉索轴向刚度
轴向荷载作用下,拉索的轴向刚度相对于钢丝会降低,轴向荷载作用下,拉索的荷载位移曲线可反映拉索的轴向刚度.为描述拉索的轴向刚度,将断丝拉索总轴力Fb除以缆索横截面积nπR2,可得到缆索截面平均轴向应力,平均轴向应力与索体长度内平均应变的比值,定义为拉索弹性模量Ecable.
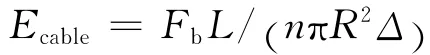
式中:n为拉索截面全部钢丝数;Δ为拉索两端相对位移量.拉索轴向荷载-位移曲线如图9所示,拉索弹性模量随螺旋角的变化曲线如图10所示.

由图9可以看出,对于给定的螺旋角,拉索荷载位移曲线满足线性关系.根据拉索弹性模量的定义,当螺旋角为86°时,考虑接触变形,拉索弹性模量为188 363MPa,约为钢丝弹性模量的95.18%;不考虑接触变形,拉索弹性模量为188 417MPa,约为钢丝弹模的95.21%.当螺旋角为80°时,考虑接触变形,拉索弹性模量为183 104MPa,约为钢丝弹性模量的92.52%;不考虑接触变形,拉索弹性模量为184 929MPa,约为钢丝弹模的93.45%.由图10可以看出,随着螺旋角的增大,拉索弹性模量经历了一个先增加后减小的过程,对于桥梁用半平行钢丝索扭绞范围(对应螺旋角86°~88°),轴向刚度最大降低4.82%;考虑接触变形时,轴向刚度要小于相应不考虑接触变形时的值.
拉索弹性模量随断丝径向位置和钢丝间摩擦系数的变化曲线分别如图11和图12所示.
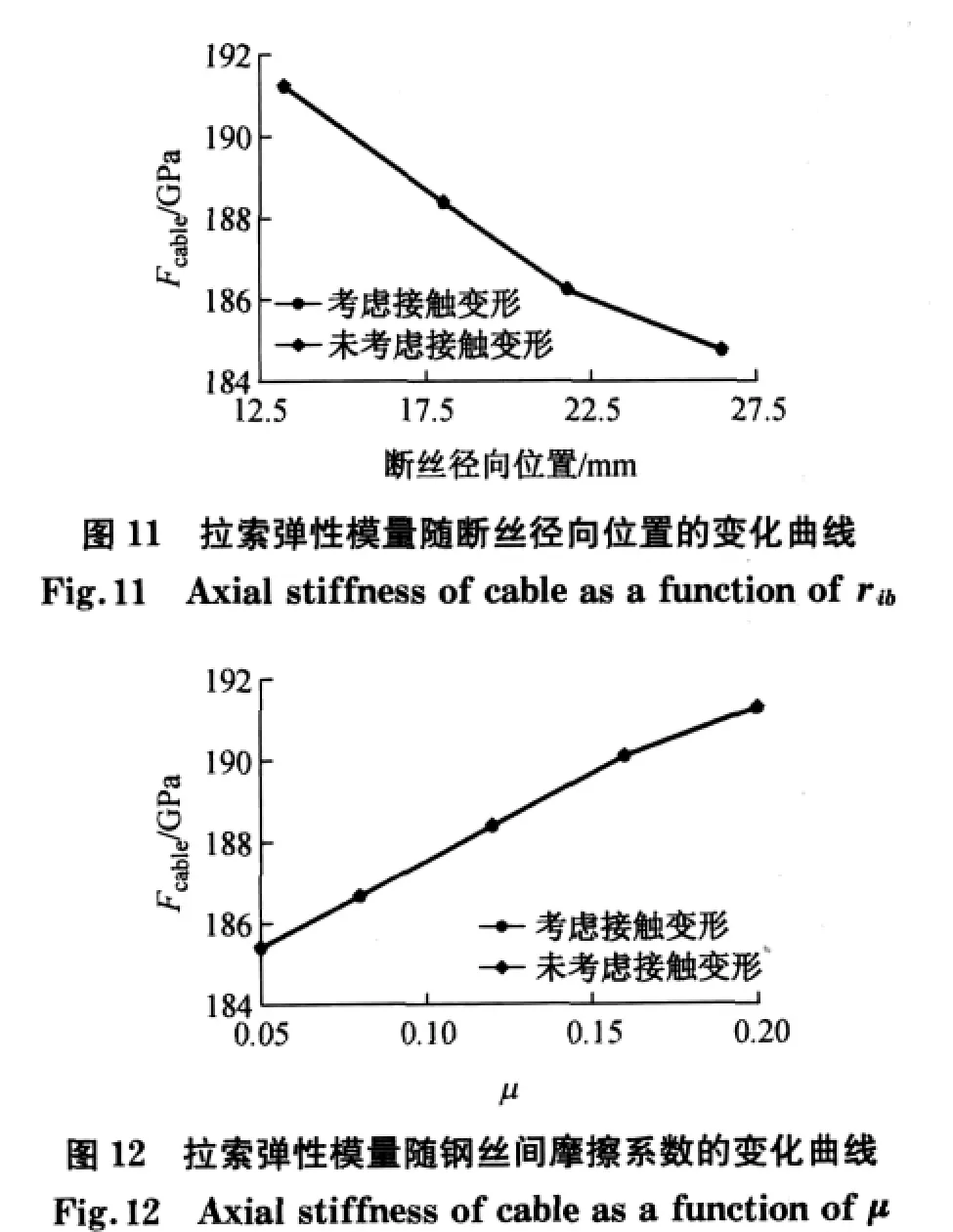
由图11可以看出,随着断丝径向位置的增大,即断丝越往外层,拉索弹性模量逐渐减小,如断丝位于第4层时,拉索弹性模量为191 200MPa,约为钢丝弹性模量的96.61%,断丝位于最外层时,拉索弹性模量为184 734MPa,约为钢丝弹性模量的93.35%.由图12可以看出,随着钢丝间摩擦系数的增大,拉索弹性模量逐渐增大,如钢丝间摩擦系数为0.05时,拉索弹性模量为185 375MPa,约为钢丝弹性模量的93.67%,钢丝间摩擦系数为0.20时,拉索弹性模量为191 258MPa,约为钢丝弹性模量的96.64%.
5 结论
考虑钢丝间的接触变形,对多层半平行钢丝索的对称断丝模型进行了修正,通过数值计算讨论了接触变形对索内钢丝拉力分布和拉索轴向刚度的影响,主要结论如下:
(1)影响长度内,钢丝拉力随到断裂处距离的增加近似线性衰减,影响长度外,各层钢丝拉力保持不变.当螺旋角为86°时,截面内钢丝拉力分布较均匀,当螺旋角为80°时,截面内钢丝拉力不均匀分布明显,随着螺旋角的增大,最大拉力增长系数逐渐变小.
(2)不论接触变形考虑与否,断丝影响长度和索力剩余系数基本保持不变.钢丝拉力增长系数随到断裂处距离的增加近似线性衰减,在断丝处不均匀分布最明显,影响长度外,拉力增长系数保持不变.当螺旋角为80°时,最大拉力增长系数为1.092;当螺旋角为86°时,最大拉力增长系数为1.070.当螺旋角为80°和86°时,考虑接触变形,最大钢丝拉力增长系数增幅分别为10.84%和1.45%.
(3)随着螺旋角的增大,拉索弹性模量经历了一个先增加后减小的过程.对于桥梁用半平行钢丝索常用参数范围,螺旋角引起轴向刚度降低最大可达4.82%,钢丝间摩擦系数引起轴向刚度降低最大可达6.33%.
实际工程中,拉索由于腐蚀、磨损等因素引起的断丝可能跨越多个钢丝层,沿长度方向也可能有多处断丝,且多为非对称断丝;同时,断丝形式、断口处的钢丝滑移等均会改变索内钢丝的拉力分布,这些因素的影响值得进一步研究.
参考文献:
[1] Raoof M,Hobbs R E.Analysis of multilayered structural strands[J].Journal of Engineering Mechanics,1988,114(7):1166.
[2] LeClair R. Axial response of multilayered strands with compliant layers[J].Journal of Engineering Mechanics,1991,117(12):2884.
[3] Nawrocki A,Labrosse M.A finite element model for simple straight wire rope strands[J].Computers and Structures,2000,77(4):345.
[4] Jiang W G,Yao M S,Walton J M.A concise finite element model for simple straight wire rope strand[J].International Journal of Mechanical Sciences,1999,41:143.
[5] Jiang W G,Warby M K,Henshall J L.Statically indeterminate contacts in axially loaded wire strand[J].European Journal of Mechanics A:Solids,2008,27:69.
[6] Seyed R G,Tanguy M,Patrice C,et al.Validity and limitations of linear analytical models for steel wire strands under axial loading using a3D FE Model[J].International Journal of Mechanical sciences,2007,49:1251.
[7] Cappa P.An experimental study of wire strains in an undamaged and damaged steel strand subjected to tensile load[J].Experimental Mechanics,1988,28(4):346.
[8] Chein C H,Costello G A.Effective length of a fractured wire in wire rope[J].Journal of Engineering Mechanics,1985,111(7):952.
[9] Colin M.Behavior of monostrand tendons with broken wires[D].London:The University of Western Ontario,2001.
[10] Raoof M,Kraincanic I.Recovery length in multilayered spiral Strands[J].Journal of Engineering Mechanics,1995,121(7):795.
[11] 李元兵.拱桥吊杆力学行为及损伤退化研究[D].上海:同济大学桥梁工程系,2008.
LI Yuanbing.Research on the mechanical behavior and damage deterioration of suspender for arch bridges[D].Shanghai:Department of Bridge Engineering of Tongji University,2008.
[12] Love.A treatise on the mathematical theory of elasticity[M].New York:Dover Publications,1944.
[13] 彭崇梅,张启伟,李元兵.桥梁半平行钢丝索的对称断丝损伤力学模型[J].同济大学学报:自然科学版,2013,41(1):20.
PENG Chongmei,ZHANG Qiwei,LI Yuanbing.Darnage model of multilayered semi-parallel wire cables for bridges with symmetric wire breaks[J].Journal of Tongji University:Natural Science,2013,41(1):20.
[14] Johnson K L.Contact mechanics[M].Cambridge:Cambridge University Press,1985.
