火灾下轴向约束钢柱性能的Shanley理论模拟
2013-05-10李国强
李国强,陈 琛
(同济大学 土木工程学院,上海 200092)
由于结构的连续性,钢框架柱在结构中会受到周围构件的约束.在局部火灾下,钢框架柱因为轴向热膨胀受到约束而产生附加轴力,从而使钢柱在较低的温度下发生屈曲;钢柱屈曲后,轴向约束会分担钢柱的荷载,使得钢柱在屈曲后仍能继续参与受力,这种现象已经在Broadgate火灾[1]和Cardington整体结构试验[2-3]中得到证实.定义钢柱的屈曲温度为钢柱发生屈曲时的温度;钢柱的临界温度为钢柱的轴力恢复到常温下的初始轴力时的温度.对于无轴向约束钢柱,在火灾下,随着温度的升高,钢柱的轴力保持不变.当温度达到钢柱的屈曲温度时钢柱发生屈曲,轴力迅速下降,因此无轴向约束钢柱的临界温度与屈曲温度相同;对于有轴向约束钢柱,随着温度的升高,由于轴向约束的存在,钢柱的轴力增大.当达到钢柱的屈曲温度时,钢柱发生屈曲,钢柱的轴力下降.由于屈曲释放了由于温度升高而产生的轴向膨胀,因此尽管构件出现负刚度但其仍能保持平衡从而继续承载,轴力随着温度的升高缓慢下降.当轴力降低到初始轴力时,钢柱达到临界温度.因此约束钢柱的临界温度将大于等于其屈曲温度,考虑屈曲后性能能提高约束钢柱的抗火能力.
Franssen[4]用有限元软件对轴向约束钢柱火灾下的受力性能进行了分析,认为轴向约束在钢柱屈曲后必然能分担钢柱荷载从而提高钢柱的抗火能力,因此可以定义钢柱的轴力恢复到初始轴力时的温度为临界温度.Wang[5]认为火灾下约束钢柱在屈曲前可以按轴心受力构件进行设计,钢柱发生屈曲时和屈曲后,约束钢柱处于轴力和弯矩共同作用下,可按压弯构件进行设计.根据以上理论对任意温度下的约束钢柱进行分析,从而得到钢柱的轴力-温度曲线.Neves等[6]提出了一个约束钢柱的简化计算模型.钢柱的轴向约束用轴向弹簧表示,转动约束用转动弹簧表示.通过对该简化模型的分析得到钢柱的轴力-温度曲线.王培军,李国强[7]运用改进的Jezék方法,也获得了钢柱的轴力-温度曲线.
约束钢柱火灾下的性能分析,由于涉及到高温下钢材的材料非线性以及钢柱的几何非线性,因此求解比较复杂.现有的分析方法均为有限元方法和数值积分方法.这两种方法对于约束钢柱的性能模拟较为精确,而且能够对钢柱的整个升温过程进行分析,从而得到钢柱的轴力-温度曲线.但是有限元方法力学概念不清晰,而数值积分方法则要通过迭代,计算相对复杂.在常温下,Shanley模型是求解钢柱受压弹塑性稳定的经典模型,力学概念清晰而且求解过程相对简单.笔者对Shanley模型进行改进,考虑轴向约束的影响,以铰链的两肢的应变作为基本未知量,并且考虑升温过程中引起的钢材的塑性变形,从而较为准确地得到钢柱的轴力-温度曲线.
1 Shanley理论模型和高温下钢材应力应变模型
1.1 Shanley理论模型
Shanley[8]在1946年设计了一个由3部分组成的弹塑性力学模型,建立了屈曲后荷载与杆件挠度之间的关系,如图1所示.用一个铰链将两根长度为l/2的刚性杆连接起来,系统所有的弹性变形和塑性变形都发生在铰链上,如图1a所示.铰链如图1b所示,有两根短肢组成,短肢长度为h,其间距离亦为h,截面面积均为A/2.材料的应力应变关系如图1c所示,铰链的弹性模量为E,切线模量为Et,为双直线模型.

图1 Shanley理论的力学模型Fig.1 Mechanical model of the Shanley theory
构件在轴向荷载P下到达构件的临界状态,构件开始弯曲.铰链处由于构件弯曲引起的应变为ε1和ε2,构件的挠度为d,端部倾角为θ,其几何关系为d=lθ/2和θ=(ε1+ε2)/2,因此

铰链处的外弯矩为

铰链处的内力矩为

假定弯曲凹面和凸面的杨氏模量分别为E1和E2,有ΔP1=ε1E1A/2和ΔP2=ε2E2A/2.代入式(3)得

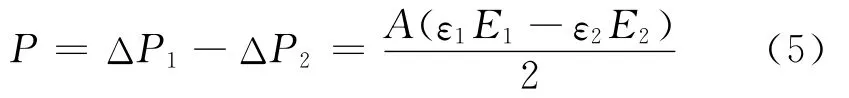
所以钢柱的轴力平衡方程为钢柱的弯矩平衡条件为Mi=Me,得到
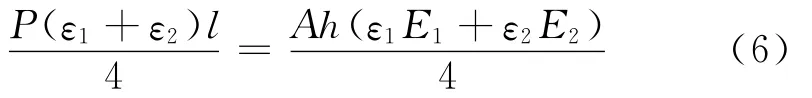
构件的受力分以下3种情况:
(1)构件处在弹性状态,有E1=E2=E.
(2)构件处在弹塑性状态,采用双模量理论,有E1=Et,E2=E.
(3)构件处在弹塑性状态,采用切线模量理论,有E1=E2=Et.
1.2 高温下钢材应力应变模型
本文采用高温下考虑塑性应变的钢材应力应变关系,假定钢材塑性应变不受温度变化的影响[9].对于理想弹塑性材料模型,钢材的应力应变关系随温度的变化如图2所示.
假设在温度t1时钢材在B点的应力应变分别为fy1和ε1,fy1为钢材在t1时的屈服应力.当温度由t1变化到t2时,应力和应变关系按如下步骤变化:

图2 考虑塑性的应力应变关系Fig.2 Stress-strain relationship of steel with consideration of plastic deformation
(1)t1时卸载,此时应力应变关系按直线BG变化,BG的斜率为t1时钢材的弹性模量Et1.
(2)钢材的残余塑性变形为直线BG与应变轴的交点G,其值为

(3)温度升至t2时,应力应变曲线沿GEF变化.在GE段为弹性段,其斜率为t2下的弹性模量Et2,塑性应变保持不变.当应力应变曲线到达EF段时,钢材的弹性应变保持不变,塑性应变增大,其值为

式中:fy2为钢材在t2时的屈服应力.
2 火灾下约束钢柱分析模型
假定约束钢柱的长度为l,钢柱两端为铰接.分析模型采用改进的Shanley理论模型,塑性铰链处的挠度为d,u0为常温下构件的轴向变形,ut为温度t时构件的轴向变形,k1为轴向约束刚度,P0和M0分别为常温下钢柱的设计轴力和设计弯矩.如图3所示.将实际钢柱转化为Shanley模型钢柱的等效原则为两者跨中截面的应变保持一致:轴向应变相同通过钢柱跨中截面面积A保持不变实现,即铰链两肢的面积均为A/2;弯曲应变相同通过跨中截面惯性矩I不变得到,取铰链部分宽度保持不变,肢件间的距离h通过式(9)得到
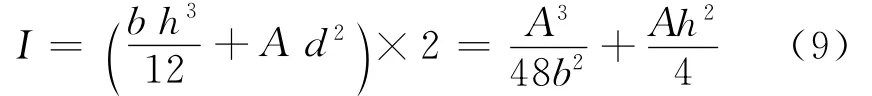
式中:b为铰链的宽度.
钢柱的轴向约束刚度k1=β1(E20A/l),且不随温度发生变化.其中β1为轴向约束刚度比;E20为20℃时钢材的弹性模量;A为构件的截面面积.
根据已有参数分析结果[10],端部弯矩比对临界温度的影响很小,因此取最不利情况端部弯矩比为-1.在常温下,轴向约束未发生变形.升温条件下,钢柱的应力应变模型按CECS200[11]的定义,考虑塑性变形的累积.应力应变正方向定义与图1b保持一致.
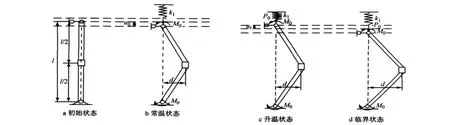
图3 火灾下约束钢柱的分析模型Fig.3 Analysis model of restrained column in fire
2.1 常温下的分析
常温时,t0=20℃.在设计轴力P0和设计弯矩M0的作用下,钢柱的铰链左肢应力应变分别为σ(t0)1和;铰链右肢应力应变分别为,因为构件处于轴力弯矩作用下,因此有.铰链处挠度为铰链处的外弯矩为
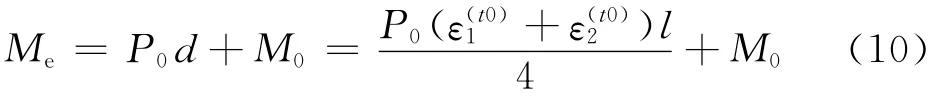
内力矩为
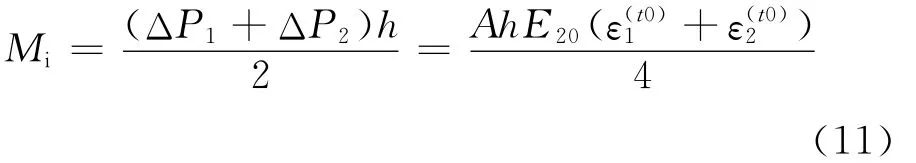
因此由弯矩平衡方程Me=Mi得

铰链处力平衡方程为
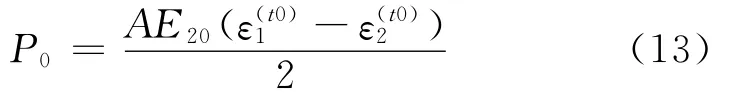

式中:kc,0=E20A/l为钢柱常温下的轴向刚度.
常温下铰链的塑性应变为

式中:ε分别为塑性铰链两肢在常温下的塑性应变.
2.2 升温下的分析
假设t1<t2,且已知在温度t1时钢柱达到平衡,铰链两肢的塑性应变分别为
当温度从t1升到t2时,铰链两肢的应力应变分别变为由图1b可知.铰链处挠度为约束钢柱柱端位移为

式中:εth为钢柱的轴向温度膨胀系数;kc,t2=Et2A/l为钢柱在t2时的轴向刚度.
式(16)与式(14)相减可得

整理得

铰链处的外弯矩为

内力矩为
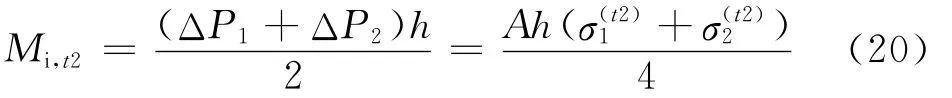
因此由弯矩平衡方程Me,t2=Mi,t2得
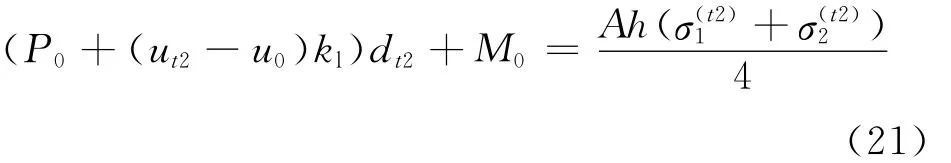
铰链处力平衡方程为

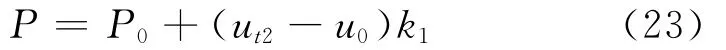
在温度为t2时,构件的受力情况根据铰链处钢材截面是否发生屈服分为两种,在此分别讨论.
(1)构件在弹性状态,铰链两肢都未发生屈服.
在温度升高后,钢柱的塑性应变没有发生变化,有
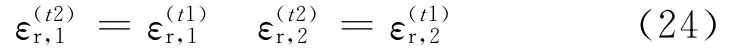
铰链两肢的应力分别为

将式(25)代入式(21)和式(22)的平衡方程中,得到
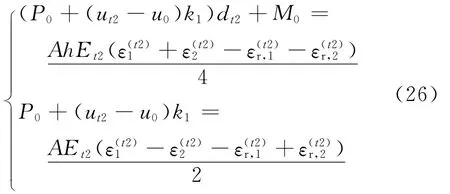
(2)构件处在弹塑性状态,采用理想弹塑性模型,左肢发生屈服.
在温度升高后,钢柱铰链的左肢发生屈服,应力达到t2下的屈服应力ft2,右肢仍然保持在弹性状态,有
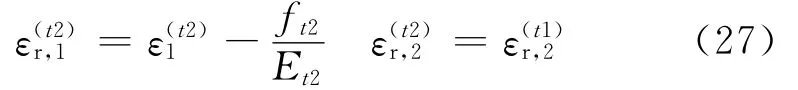
铰链两肢的应力分别为

将式(28)代入式(21)和式(22)的平衡方程中,得到

钢柱的受力状态在不同的升温阶段其判别准则如下:
(1)屈曲温度以前,通过约束钢柱是否达到构件的极限荷载来判别.
对于压弯构件而言,构件达到极限荷载可能导致构件进入塑性,但其跨中截面应力可能还未达到其屈服强度.因此,本文引入整体稳定的判定准则.
根据常温下的无约束钢柱在轴力和弯矩共同作用下的临界温度的计算公式,考虑轴向约束刚度的影响,不考虑截面塑性发展,得到火灾条件下约束钢柱在轴力和弯矩共同作用下的屈曲温度判定公式为

式中:N为考虑轴向约束时高温下的轴力;Ncr,T为高温下的屈曲轴力;M0为常温下的弯矩;W为截面模量;N′EX为参数.
如果满足式(30),构件因屈曲进入弹塑性阶段,也采用式(29)求解.否则,继续采用式(26)求解.
(2)屈曲温度以后,通过铰链左肢应变是否达到钢材的屈服应变来判别.
在屈曲温度以后,对于轴向约束钢柱两种不同的受力情况最明显的区别就是左肢是否达到极限荷载.但是由于在计算中采用了理想弹塑性模型,钢材屈曲后通过应力不能得到应变值,所以在此采用其应变作为判别准则.
对于时间t2,铰链左肢应变为ε(t2)1,钢柱左肢在时间t1时的塑性应变为ε(t1)r,1,因此在时间t2时,左肢进入屈曲的判别条件为
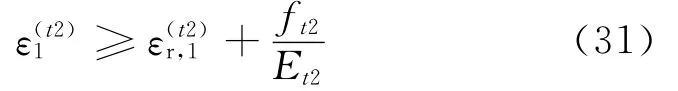
如果满足式(31),构件进入弹塑性阶段,则采用式(29)求解.如果不满足,则构件还在弹性阶段,继续采用式(26)求解.
3 理论分析的求解
理论分析的目的是得到约束钢柱在升温条件下的轴力温度曲线.理论分析所建立的上述方程,可通过以下步骤求解:
Step1 输入初始参数为钢柱长度l、初始荷载P0、初始弯矩M0、截面面积A、惯性矩I、截面高度h和宽度b、钢材屈服强度f0和弹性模量E0.
Step2 初始条件定义为温度t=20℃,初始塑性应变ε(t0)r,1=ε(t0)r,2=0.
Step3 根据常温下的平衡方程(式(12)、式(13))得到常温下的铰链两肢的应变.
Step4 根据式(13)得到常温下平衡时的钢柱轴力,输出轴力和温度.
Step5 温度t=t+Δt.
Step6 根据式(26),解得温度t+Δt下钢柱铰链两肢的应变.
Step7 根据式(30)判断钢柱是否发生屈曲,如果发生则到Step9.
Step8 根据式(31)判断钢柱铰链左肢是否发生塑性变形,如未发生屈曲,则到Step11.
Step9 根据式(29),重新解得温度t+Δt下钢柱铰链两肢的应变.
Step10 根据式ε(t2)r,1=ε(t2)1-ft2/Et2更新钢柱左肢的塑性应变.
Step11 由式(16)得到在温度t+Δt下,钢柱的轴向变形.
Step12 由式(23)得到温度t+Δt下钢柱的轴力,输出轴力和温度.
Step13 判断温度是否小于950℃,是则到Step5.
Step14 结束.
根据最后输出的钢柱轴力-温度曲线即可以确定钢柱的屈曲温度和临界温度.
4 验证
为了验证本文提供的基于改进的Shanley模型的理论分析方法的正确性,利用经验证的ABAQUS有限元模型[9]和本文的理论分析方法对同一钢柱进行分析,对结果进行比较.验证分析选取的约束钢柱截面为H形截面,尺寸为H200mm×6mm×150 mm×8mm,沿长度方向保持不变,常温下的钢材的屈服强度为345N·mm-2,弹性模量为2.05×105N·mm-2,绕弱轴转动.本文分析方法采用的应力应变关系是CECS200[11]的模型.ABAQUS模拟采用的空间线性两节点梁单元B31,沿柱长方向划分为50个单元.轴向约束通过点对点弹簧单元SPRING2模拟,并设定能量耗散系数αd的方法引入虚拟的粘滞阻尼力帮助收敛.
4.1 火灾下约束钢柱受力性能分析结果比较
ABAQUS有限元模型与Shanley方法对于火灾下约束钢柱在轴力和弯矩共同作用下的受力性能的分析结果如图4所示,以轴向约束刚度比β1来表征.Shanley方法的分析结果与ABAQUS有限元模型的分析结果保持一致.在整体受力过程中,Shanley方法与ABAQUS有限元模型的结果都符合很好,在轴向约束较大的情况下,屈曲后的曲线与ABAQUS有限元模型有一定差别,但是相差不大.因此,通过本文改进的Shanley方法,可以得到与ABAQUS有限元计算精度基本一致的轴力-温度曲线.本文模型可以用于对约束钢柱火灾下性能的分析.

图4 火灾下约束钢柱受力性能分析结果比较Fig.4 Comparison on columns performance of ABAQUS predication and Shanley method calculation in a fire
4.2 火灾下约束钢柱临界温度分析结果比较
ABAQUS有限元模型与Shanley方法对于火灾下约束钢柱在轴力和弯矩共同作用下的受力性能的分析结果如图5所示.在轴向约束刚度比较小时,Shanley方法得到的临界温度与ABAQUS有限元模型得到的临界温度一致.当轴向约束刚度比较大时,运用Shanley方法得到的临界温度略低于由ABAQUS有限元得到的临界温度,最大差值约为70℃.造成差异的主要原因可能是在轴向约束刚度比较大的情况下,钢柱的塑性应变较大,而Shanley方法采用的是简化模型,其塑性变形与原钢柱不完全一样,所以两者得到的临界温度略有不同.总体而言,对于常用的轴向约束刚度比而言,Shanley方法能对约束钢柱的抗火性能给出较为精准的描述.
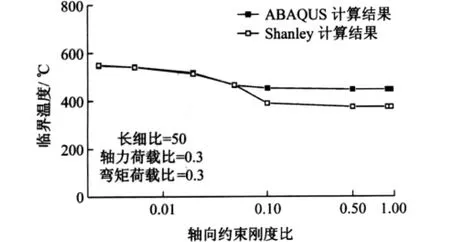
图5 火灾下约束钢柱临界温度分析结果比较Fig.5 Comparison on critical temperature of the restrained column of ABAQUS predication and Shanley method calculation in a fire
5 结论
本文运用改进的Shanley简化模型对约束钢柱的抗火性能进行分析.由于Shanley模型在力学上比较明确、简明,因此用此方法对约束钢柱进行分析能够比较清楚地了解到在火灾条件下钢柱的受力和变形过程.模型考虑了轴向温度膨胀、轴向约束刚度、钢材的塑性应变等因素的影响,通过与ABAQUS有限元软件的计算结果对比验证,证明运用本文的分析方法能够较为准确地得到钢柱的轴力温度曲线,进而得到约束钢柱的临界温度,可以为约束钢柱的抗火设计提供一种简单的力学模型.
[1] SCIF.Investigation of broadgate phase 8fire[R].Ascot:SCIF Fire Engineering Group,1991.
[2] Lennon T,Simms C.Elevated temperature column tests:results from phase 1.tech.rep[R].Garston:Building Research Establishment,1993.
[3] Lennon T.Elevated temperature column test:results from phase 2[R].Garston:Building Research Establishment,1994.
[4] Franssen J M.Failure temperature of a system comprising a restrained column submitted to fire[J].Fire Safety Journal,2000,34(2):191.
[5] WANG Y C.Postbuckling behavior of axially restrained and axially loaded steel columns under fire conditions[J].Journal of Structural Engineering,2004,130(3):371.
[6] Neves I C.The critical temperature of steel columns with restrained thermal elongation[J].Fire Safety Journal,1995,24(3):211.
[7] 王培军,李国强.轴向约束钢框架柱火灾升温下屈曲后性能研究 [J].同济大学学报:自然科学版,2008,36(4):6.
WANG Peijun,LI Guoqiang.Post-buckling behavior of axially restrained steel columns in fire[J].Journal of Tongji University:Natural Science,2008,36(4):6.
[8] Shanley F R.Inelastic column theory[J].Journal of the Aeronautical Sciences,1947,14(4):261.
[9] 李国强,韩林海,楼国彪,等.钢结构及钢-混凝土组合结构抗火设计[M].北京:中国建筑工业出版社,2006.
LI Guoqiang,HAN Linhai,LOU Guobiao,et al.Fire protection design of steel structure and steel-concrete composite structures[M].Beijing:China Architecture and Building Press,2006.
[10] 陈琛.约束钢柱抗火性能实用设计方法[D].上海:同济大学土木工程学院,2011.
CHEN Chen.Design method of restrained steel columns in fire[D].Shanghai:College of Civil Engineering of Tongji University,2011.
[11] 中国工程建设标准化协会.CECS200:2006建筑结构防火技术规范 [S].北京:中国计划出版社,2006.
China Association for Engineering Construction Standardization.CECS200:2006 Technical code for fire safety of steel structure in buildings[S].Beijing:China Planning Press,2006.
