应力旋转对同济一号模拟月壤变形特性的影响
2013-05-10蒋明镜李立青
蒋明镜,李立青,3,刘 芳,王 闯
(1.同济大学 岩土及地下工程教育部重点实验室,上海 200092;2.同济大学 地下建筑与工程系,上海 200092;3.河南省交通科学技术研究院有限公司,河南 郑州 450006;4.中国空间技术研究院,北京 100094)
目前,以月球软着陆探测与自动巡视勘察为目标的月球探测二期工程[1]正在进行.未来登月成功后月球车辆的行驶、月球基地建设过程中相应的基坑开挖及基础受力均与主应力轴旋转有关.已有成果表明,在交通、地震、波浪荷载作用下以及基坑开挖时,主应力幅值随时间变化,主应力轴也发生偏转;且即使其他应力参量不变,主应力轴的纯旋转也会使土体产生明显的塑性变形,对于某些土而言甚至会发生破坏[2-10].因此对月壤在主应力轴旋转情况下变形特性的研究对于月球基地的建设乃至月球能源的开发利用均有重要意义,然而目前此类研究尚未见报道.考虑到真实月壤样品极其珍贵,采用与月壤物理力学性能相近的模拟月壤进行间接研究是目前切实可行的办法之一.笔者在郑永春[11]等调查基础上已成功研制出力学性能与月球表面月海区域月壤相近的同济一号模拟月壤(简称TJ-1模拟月壤)[12-13],为通过室内试验间接研究月壤在主应力轴旋转时的变形特性提供了试验基础.
根据文献[14]可将月壤及模拟月壤归类为砂性土.砂性土在主应力轴旋转方面的研究成果多是在中主应力系数b=0.5条件下得到的,仅部分学者研究了主应力轴旋转条件下b值对土体变形特性的影响[9-10];且主应力轴旋转条件下砂性土变形性能的研究一般以饱和样为对象,干砂性能的研究尚未见报道.由文献[15]中的试验及数值模拟结果可知,不同重力场下土体经历相同应力路径时其变形特性是相似的,为此本文拟在地球重力场下以干燥TJ-1模拟月壤为原材料,采用空心圆柱扭剪仪进行两个系列的主应力轴旋转试验,以研究主应力轴旋转条件下平均应力p、中主应力系数b对TJ-1模拟月壤的变形特性及非共轴性能的影响.
1 TJ-1模拟月壤
TJ-1模拟月壤是在郑永春[12]等调查基础上以吉林省靖宇县境内的红色火山灰为原材料,经过烘干、粉碎、筛分,在部分真实月壤样品的级配曲线范围,通过级配调整、力学测试获得符合目标力学指标的级配方案.TJ-1模拟月壤的主要物理力学指标如下:有效粒径d10=20μm;中值粒径d50=260μm;不均匀系数Cu=21.5;曲率系数Cc=0.92;相对密度为2.72;含水率小于1%;孔隙比为1.0时,密度为1.36g·cm-3,内摩擦角为47.6°,黏聚力为0.86 kPa;法向压力范围为12.5~100kPa时压缩指数为0.086.TJ-1模拟月壤的物理力学参数与月球表面月海区域0~30cm深度月壤的相应参数最佳估计值的符合情况见表1.符合情况采用符合度表示,即若该参数在相应估计值上、下限范围之内其符合度为100%,否则采用该参数与最接近的上限或下限的比值表示.以TJ-1模拟月壤的力学性能作为主要控制指标,若符合度超过95%,即可认为该项指标满足要求.分析表1并结合文献[12]可知,TJ-1模拟月壤的主要力学特性基本在月球表面月海区域0~30cm深度月壤相应参数的最佳估计值范围之内;与国内外其他模拟月壤相比,TJ-1模拟月壤具有级配更加稳定,较大孔隙比时抗剪强度高的特点,可用于模拟月球表面月壤的力学特性.
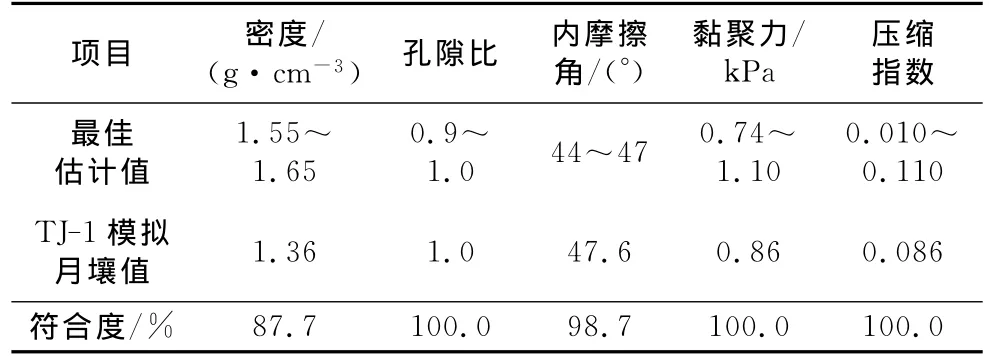
表1 TJ-1模拟月壤部分物理力学参数与相应的最佳估计值Tab.1 Comparison between TJ-1and best estimate values
2 试验条件
试验所用仪器为GDS(Global Digital Systems)空心圆柱扭剪仪,文献[16]已对该设备进行详细描述,在此仅简要介绍.空心圆柱扭剪仪主要由4部分组成(图1),即压力室及伺服控制系统、围压(包括反压)系统、数据控制及采集系统、计算机控制系统;对于砂性土试样还需真空装置,在试样装入压力室的过程中施加一定的负压,使其自行站立.可通过内外室压力、扭矩以及轴力的组合实现土体不同应力路径的加载.图2、图3为空心圆柱试样的加载参数及薄壁单元体上的应力状态示意图.


图3 典型单元体的应力分布Fig.3 State of stress in the specimen
空心圆柱试样相对密度Dr=53%±2%,对应于月球表面月海区域0~30cm深度时的密实程度.试样分5层制备,首先利用分层欠压法与冰冻法相结合生成的均匀实心圆柱样确定每层的高度,而后采用砂雨法与插捣法相结合制备相对均匀的空心圆柱试样,制作方法已在文献[17]中描述,试样的可重复性已进行验证[17-18].试验中 TJ-1模拟月壤空心圆柱试样达到设定的应力状态固结30min后,采用空心圆柱扭剪仪加载系统中的应力路径加载模块进行主应力轴旋转试验.应力路径模块由平均应力p、偏应力q、中主应力系数b、主应力方向α等参量控制,可在内、外压允许范围内通过改变上述参量实现不同的加载方式.各参量表达式如下:

此外,还涉及到反映TJ-1模拟月壤强度发挥程度的偏应力比,即

本文共进行两个系列的试验.试验系列Ⅰ为中主应力系数b不同情况下主应力轴的旋转试验,即对一个试样,保持平均应力p、偏应力q不变,主应力方向以ω=0.1(°)·s-1速度在75°~-75°旋转;对于不同试样则进行不同b值的主应力轴旋转试验,以研究中主应力系数b对TJ-1模拟月壤各应变分量及非共轴现象发展的影响.系列Ⅰ进行了p=100 kPa,q=43kPa,b值分别为0.2,0.5,0.9的主应力轴在75°~-75°旋转试验.系列Ⅱ为平均应力系列的主应力轴旋转试验,即对一个试样,加载过程中保持p,η,b不变,主应力方向以ω=0.1(°)·s-1速度在0°~90°旋转;对于不同试样则给定不同的平均应力进行主应力轴旋转试验,以研究平均应力对TJ-1模拟月壤变形特性的影响.系列Ⅱ进行了b=0.5、η=0.866,p分别为50,100,200kPa的主应力轴0°~90°的旋转试验.具体方案见表2.
应当指出,系列Ⅰ中,主应力轴的旋转范围未选择在0°~180°内是因为从α=0°进行主应力轴旋转时,主应力方向在0°和180°方向上跳跃,试验无法进行.

表2 试验方案Tab.2 Test scheme
上述两个试验系列的应力变化情况若用σ1,σ2,σ3,α表示,则使3个主应力值不变,主应力方向发生连续偏转,相应的应力分量可表示为

试验过程中所有试样均保持干燥状态,各应力分量与其有效应力分量相等.下文将对各应变分量的确定进行简单描述.图4为试验前、后空心圆柱试样尺寸变化的示意图.各应变分量的计算分析前,首先对试验后试样的内、外半径采用式(10)、式(11)分别进行修正.

图4 空心圆柱试样剪切前、后的尺寸变化Fig.4 Schematic diagram of dimensional changes after the test

式(10),(11)中:ro,Ro分别为固结完成后空心圆柱试样的内、外半径;r,R分别为剪切至某时刻的内、外半径;Ho为试样固结完成后的高度;H为剪切至某一时刻的高度;ΔVint为剪切过程中内压力室水的体积变化;ΔVb为剪切过程中试样发生的体积变化;ΔVint,ΔVb由内压、反压控制器根据排出/吸入水的体积测得,若进行不排水剪切或试样在剪切过程中保持干燥,则ΔVb=0.
由图4可推得各应变分量的表达式如下:
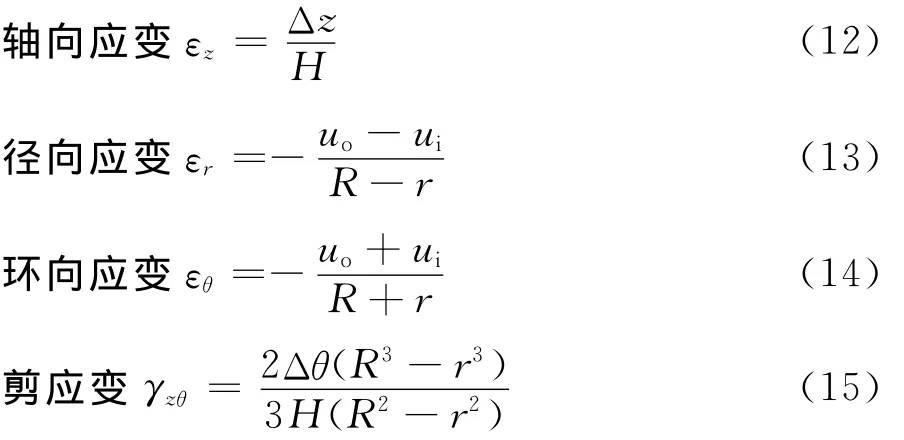
式中:ui,uo为图4中剪切过程中内外半径的变化量;Δθ为试样发生转动的角度.
规定本文中各应变分量均以压缩为正.还需指出,TJ-1模拟月壤试样在试验过程中需保持干燥,体变无法根据排水量直接测得,可由εv=εz+εr+εθ计算得到.考虑到乳胶膜嵌入量很小,分析体变规律时未考虑乳胶膜嵌入的影响.
3 主应力轴旋转对变形特性的影响
3.1 中主应力系数对应变发展的影响
图5a~5c为系列Ⅰ中各试样应力主轴旋转过程中应变分量的变化情况.系列Ⅰ中应力主轴的偏转范围为75°~-75°,即主应力方向逐渐向土体沉积方向偏转,与其重合后又偏离沉积方向.各应变分量起点所对应的应力状态应为p=100kPa,α=0°,而图5a~5c中各应变起点所对应的应力状态为p=100kPa,α=75°,虽然两者的起点不同,但应变的变化规律基本相同,且后者数据处理更为方便.由图5可知,系列Ⅰ中中主应力系数b对各应变分量的发展影响显著:①对于轴向应变εz,由式(6)可知,应力主轴旋转使试样的轴向应力增加,故各试样的轴向应变均表现为压缩应变.b值从0.2到0.9变化时,轴向应力减小,相应的轴向应变也呈减小趋势.②对于环向应变εθ,由式(7)可知,应力主轴旋转使试样的环向应力减小,故相应的环向应变主要为拉伸应变.随b值的增加,拉伸应变呈增大趋势,但增幅相对较小.③对于径向应变εr,由式(8)可知,径向应力即为中主应力,径向应力反映的是对试样径向的约束情况.由图5可知,随着b值的增加,径向约束增大,相应的径向应变逐渐由拉伸应变向压缩应变变化.④对于剪应变γzθ,应力主轴旋转过程中剪应变呈类似正弦规律变化,应力主轴旋转至-30°左右时剪应变为零,且α=75°与α=-75°时γzθ在数值上并不相等,由此可知应力主轴的旋转使TJ-1模拟月壤产生了明显的塑性变形.进一步分析可知,随b值的增大,γzθ呈增大趋势.

图5 应变分量与主应力方向的关系曲线(系列Ⅰ)Fig.5 Strain components and principal stress directions(SeriesⅠ)
3.2 应变分量随平均应力的变化情况
系列Ⅱ中各试样的应变分量与应力主轴旋转角度的关系曲线如图6所示.系列Ⅱ中应力主轴的偏转范围为0°~90°,即主应力方向从土体的沉积方向向垂直于沉积方向偏转.由图6可知,应力主轴的旋转同样使TJ-1模拟月壤产生明显的塑性变形,且平均应力对各应变分量的发展趋势影响显著:①对于轴向应变εz,应力主轴旋转时产生的轴向应变主要为拉伸应变,且随平均应力p的增加呈增大趋势.②对于环向应变εθ,应力主轴旋转产生的应变主要为压缩应变;平均应力p=50,100kPa时其随应力主轴的旋转发展趋势基本一致,p=200kPa时有所增加.③对于径向应变εr,其变化情况与平均应力的大小密切相关.平均应力p=50kPa时,径向应变为拉伸应变,且随应力主轴的旋转呈增大趋势;p=200 kPa时径向应变前期为压缩应变,随应力主轴的旋转逐渐转化为拉伸应变.④对于剪应变γzθ,应力主轴旋转产生的剪应变随平均应力的增加整体呈减小趋势.应力主轴旋转至90°时剪应力为零,但剪应变分量并未回落至零点,由此可知该试验系列中应力主轴的旋转同样使TJ-1模拟月壤产生了明显的塑性变形.上述各应变分量的发展规律可解释如下:制样过程中TJ-1模拟月壤遭受重力、插捣作用以及应力主轴旋转前主应力方向与轴向应力方向一致,导致试样沿轴向压缩性小,膨胀性大.应力主轴旋转时,由公式(6),(7)可知,轴向应力σz减小、环向应力σθ增大,这种应力的变化情况对应两者的优势变形趋势,从而导致试样产生拉伸轴向应变和压缩环向应变.对于不同的平均应力p,应力主轴偏转使得σz,σθ变化的幅度也不相同:p越大,σz的减小量越大,相应的拉伸应变也越大;σθ的增加量越大,产生的压缩应变也越大.对于给定p值,径向应力σr在应力主轴的偏转过程中保持不变,但随p值的增加,σr对试样的径向约束不断增强,径向应变逐渐由压缩应变转化为拉伸应变.
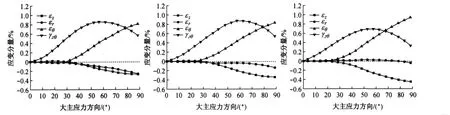
图6 应变分量与主应力方向的关系曲线(系列Ⅱ)Fig.6 Strain components and principal stress directions(SeriesⅡ)
3.3 体应变的变化规律
图7为系列Ⅰ中应力主轴偏转过程中体应变的发展情况.由图7可知,主应力轴75°~-75°旋转使得各TJ-1模拟月壤试样的体变均呈剪胀现象;且体应变的发展趋势随中主应力系数b的增加呈先减小后增大趋势,b∈[0.2,0.9]范围内剪胀现象呈减弱趋势,b=0.2时剪胀最为明显,b=0.9时剪胀现象最弱,这也与3.1节中各应变分量的发展趋势相吻合.

图7 体应变与主应力方向的关系曲线(系列Ⅰ)Fig.7 Volumetric strain and principal stress directions(SeriesⅠ)
图8为系列Ⅱ中TJ-1模拟月壤主应力方向在0°~90°偏转时体应变的发展情况.由图8可知,主应力轴旋转的开始阶段体积变化不明显,在旋转至30°之后开始呈剪缩现象,且随偏转角的增大,剪缩现象越来越明显.且通过图8可以发现,即使偏应力比η、中主应力系数b不变,主应力轴旋转过程中TJ-1模拟月壤试样的剪缩现象随平均应力的增大也愈加明显.
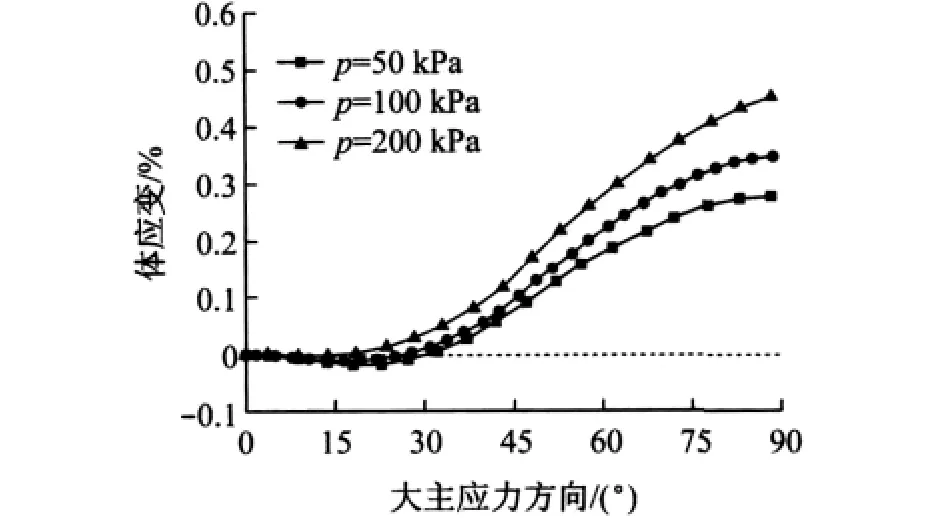
图8 体应变与主应力方向的关系曲线(系列Ⅱ)Fig.8 Volumetric strain and principal stress directions(SeriesⅡ)
4 主应力轴旋转对非共轴特性的影响
由文献[8-9]可知,主应力轴旋转时砂样均表现出非共轴性,即主应力轴旋转过程中主应变增量方向与主应力方向不一致.非共轴性是土体受力变形过程中表现出的一种基本性质,它的存在会导致土体的宏观力学响应“变软”;若忽略这一特性而采用传统塑性理论进行工程设计,实际工程将偏不安全[19].土体的非共轴性数值上常用主应变增量方向α-与主应力方向间的夹角(非共轴角β[20])表示,即
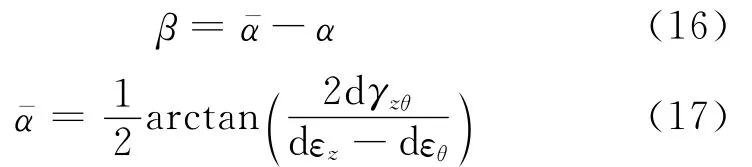
图9为试验系列Ⅰ中b=0.2时主应力轴旋转过程中主应变增量方向叠加在应力路径上的结果.图10为不同中主应力系数b情况下非共轴角β在主应力轴旋转过程中的变化情况.文献[8]指出,砂性土的变形中绝大部分为塑性应变,弹性应变可以忽略不计,故图9中总的主应变增量方向可近似认为是塑性应变增量的方向.由图9可知,主应力轴循环过程中TJ-1模拟月壤具有明显的非共轴现象(若共轴,则应变增量应垂直于弧线),主应变增量方向基本处于主应力与主应力增量方向之间,且具有明显的分段性:α在45°~0°旋转时,非共轴角β逐渐减小,0°附近达到最小值(β接近-45°),在0°~-45°时则呈增大趋势;且由图10可知,在b∈[0.2,0.9]时,非共轴角随主应力轴旋转的变化规律相似,非共轴角β的变化范围基本为[-45°,-20°].由此可见,b∈[0.2,0.9]时,b值对 TJ-1模拟月壤的非共轴性影响较小.

图9 b=0.2时应变增量方向(系列Ⅰ)Fig.9 Directions of strain increments,b=0.2(SeriesⅠ)
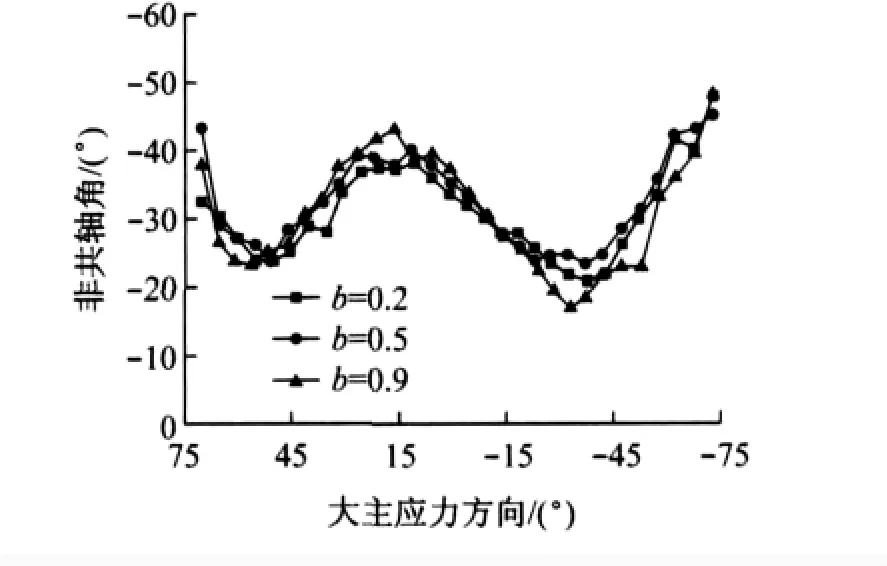
图10 非共轴角与主应力方向的关系曲线(系列Ⅰ)Fig.10 Non-coaxial angle and principal stress directions
图11为系列Ⅱ中各试样的主应变增量方向叠加在应力路径上的结果.由图11可知,系列Ⅱ中TJ-1模拟月壤在主应力轴旋转时同样呈明显的非共轴现象,且主应变增量方向介于主应力方向与主应力增量方向之间.以p=100kPa为例,非共轴角β随主应力轴的旋转呈先减小后增大的变化趋势,β在α=45°附近达到最小值.但偏应力比η、中主应力系数b恒定时,主应力轴旋转过程中平均应力的变化对TJ-1模拟月壤的非共轴现象影响并不明显,不同平均应力时非共轴角的变化规律几乎相同.

图11 应变增量方向(系列Ⅱ)Fig.11 Directions of strain increments(SeriesⅡ)
5 结论
以TJ-1模拟月壤为原材料,采用空心圆柱扭剪仪进行了主应力轴旋转情况下中主应力系数、平均应力对干燥TJ-1模拟月壤变形特性及非共轴性影响的试验研究,得出的主要结论如下:
(1)主应力轴旋转可致使TJ-1模拟月壤产生明显的塑性变形,且平均应力和中主应力系数对各应变分量的发展趋势影响显著.
(2)主应力轴的逆时针旋转可使TJ-1模拟月壤出现剪胀趋势,而顺时针旋转导致剪缩趋势,这与主应力轴旋转时主应力方向的初始点及旋转过程中主应力的变化情况密切相关.
(3)偏应力比、中主应力系数恒定情况下主应力轴旋转时平均应力对TJ-1模拟月壤的非共轴现象影响不明显,不同平均应力时非共轴角与主应力方向的变化规律几乎相同.
(4)平均应力、偏应力比恒定时主应力轴旋转过程中,中主应力系数对TJ-1模拟月壤的非共轴性影响较小.
[1] 欧阳自远.月球科学概论[M].北京:中国宇航出版社,2005.
OUYANG Ziyuan.Introduction of lunar sciences[M].Beijing:China Astronautic Publishing House,2005.
[2] Ishihare K,Towhata I.Sand response to cyclic ration of principal stress direction as induced by wave loads[J].Soils and Foundations,1983,23(4):11.
[3] Miura K,Miura S,Toki S.Deformation behavior of anisotropic sand under principal stress axes rotation [J].Soils and Foundations,1986,26(1):36.
[4] Wijewickreme D,Vaid YP.Behavior of loose sand under simultaneous increase in stress ratio and principal stress rotation[J].Canadian Geotechnical Journal,1993,30:953.
[5] Nakata Y,Hyodo M,Murata H,et al.Flow deformation of sands subjected to principal stress rotation [J].Soils and Foundations,1998,38(2):115.
[6] 姚仰平,谢定义.振动拉压扭剪三轴仪及其试验研究[J].西安建筑科技大学学报,1996,28(2):129.
YAO Yangping, XIE Dingyi. Extension-compression and torsion vibrating triaxial apparatus and experimental investigation[J].Journal of Xi’an University of Architecture &Technology,1996,28(2):129.
[7] 郭莹,栾茂田,何杨,等.主应力方向循环变化对饱和松砂不排水动力特性的影响[J].岩土工程学报,2005,27(4):403.
GUO Ying,LUAN Maotian,HE Yang,et al.Effect of variation of principal stress orientation during cyclic loading on undrained dynamic behavior of saturated loose sands [J].Chinese Journal of Geotechnical Engineering,2005,27(4):403.
[8] Gutierrez M,Ishihara K,Towhata I.Flow theory for sand during rotation of principal stress directions[J].Soils and Foundations,1991,31(4):121.
[9] 童朝霞,张建民,于艺林,等.中主应力系数对主应力轴循环旋转条件下砂土变形特性的影响[J].岩土工程学报,2009,31(6):946.
TONG Zhaoxia,ZHANG Jianmin,YU Yilin,et al.Effects of intermediate principal stress parameter on deformation behavior of sands under cyclic rotation of principal stress axes[J].Chinese Journal of Geotechnical Engineering,2009,31(6):946.
[10] Yang Z X.Investigation of fabric anisotropic effects on granular soil behavior [D].Hong Kong:The Hong Kong University of Science and Technology,2005.
[11] 郑永春.模拟月壤研制与月壤的微波辐射特性研究[D].北京:中国科学院,2005.
ZHENG Yongchun.Development of lunar soil simulants and characteristic of microwave radiation of lunar regolith[D].Beijing:Chinese Academy of Sciences,2005.
[12] 蒋明镜,李立青.TJ-1模拟月壤的研制[J].岩土工程学报,2011,33(2):209.
JIANG Mingjing,LI Liqing.TJ-1 lunar soil simulant[J].Chinese Journal of Geotechnical Engineering,2012.33(2):209.
[13] JIANG Mingjing,LI Liqing,SUN Yugang.Properties of TJ-1 lunar soil simulant[J].Journal of Aerospace Engineering,2012,25(3):463.
[14] Carrier WD.Particle size distribution of lunar soil[J].Journal of Geotechnical and Geoenvironmental Engineering.2003,129(10):956.
[15] Nakashima H,Shioji Y,Tatayama K,et al.Specific cutting resistance of lunar regolith simulant under low gravity conditions[J].Journal of Space Engineering.2008,1(1):58.
[16] 柳艳华.天然软黏土屈服特性及主应力轴旋转效应研究[D].上海:同济大学土木工程学院,2010.
LIU Yanhua.On yielding characteristics and principal stress rotation in natural soft clay[D].Shanghai:College of Civil Engineering in Tongji University,2010.
[17] JIANG Mingjing,SHEN Zhifu,LI Liqing,et al.A novel specimen preparation method for TJ-1 lunar soil simulant in hollow cylinder apparatus[J].Journal of Rock Mechanics and Geotechnical Engineering,2012,4(4):312.
[18] 蒋明镜,李立青,刘芳,等.主应力方向和偏应力比对TJ-1模拟月壤各向异性的影响[J].岩土力学,2013,34(1):6.
JIANG Mingjing,LI Liqing,LIU Fang,et al.Effects of principal stress direction and deviatoric stress ratio on deformation behavior of TJ-1 lunar soil simulant[J].Soil and Rock Mechanics.2013,34(1):6.
[19] Yu H S,Yuan X.The importance of accounting for non-coaxial behavior in modeling soil-structure interaction [C ]//Prediction,Analysis and Design in Geomechanical Applications,Bolognia:Patron Editore,2005:709-718.
[20] 史宏彦,谢定义,汪闻韶.平面应变条件下主应力轴旋转产生的应变[J].岩土工程学报,2001,23(2):162.
SHI Hongyan,XIE Dingyi,WANG Wenshao.Strain due to rotation of principal stress axes under plane strain condition[J].Chinese Journal of Geotechnical Engineering,2001,23(2):162.
