两外角平分线相等的三角形性质的探讨

叶建耀

摘 要：如果三角形的两个外角平分线相等，那么其是否为等腰三角形，针对这一点做着重论述，为相关教学工作者提供了一定的参考和借鉴。

关键词：三角形；外角平分线；等腰三角形

一、两外角平分线相等的三角形研究进展

在19世纪时学术界出现过这样的命题：“两内角平分线相等的三角形是等腰三角形。”据莱莫斯发现这个命题之后，对于这个命题正确与否的问题很难由几何方法来实行证明，因此，也引发学术界对命题研究的兴致。随之而后，几何学家斯坦纳对这个命题做出了证明，并且得到了学术界的广泛认同。随后，人们的视线逐渐转移，开始转移到"三角形的两个外角平分线相等是否是等腰三角形"的研究上，并于1989年蒋x先生解决了“位于一角对边同侧的另两外角平分线相等的三角形是等腰三角形”的问题，此后人们对这个问题的讨论也越来越激烈，但是却没有得到公认的方式证明出两外交平分线相等的三角形为等腰三角形，故而本文对此作出证明研究，以求为相关教学工作者提供更多的证明方法。

二、三角形的两外角平分线相等为等腰三角形的研究

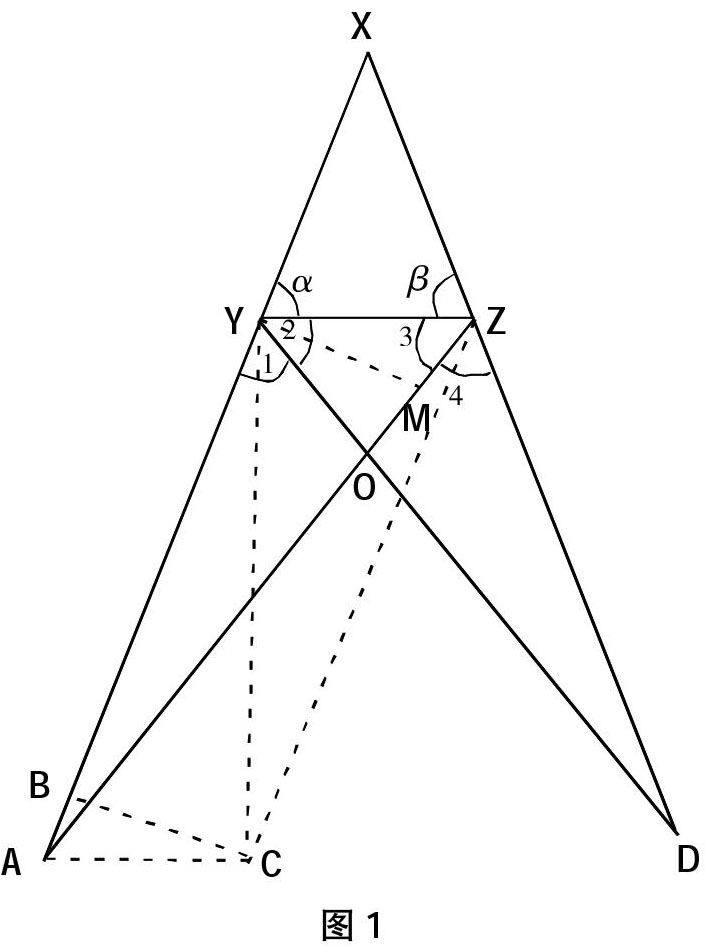
已知：△XYZ的旁心O与两外角平分线YD和ZA在YZ边的同侧，YD=ZA，如图1所示。

求证：XY=XZ或∠α=∠β

证明：过A、Z两个点作∠ZAC=∠ZYD，∠AZC=∠D，与AC相交于C。

YD=ZA？圯△ZAC≌△DYZ？圯AC=YZ、ZC=ZD、∠YZD=∠ZCA

∵∠3=∠4=∠X+∠XAZ=∠X+∠YAZ

∠ZAC=∠2=∠1=∠X+∠D

∴∠YAC=∠YAZ+∠ZAC=∠YAZ+∠X+∠D

∠YZC=∠YZA+∠AZC=∠X+∠XAZ+∠D

由此？圯∠YAC=∠YZC.

然后过Y、C两点作YM⊥ZC于M点，CB⊥YA于B点，连接YC后，Rt△ABC≌Rt△ZMY？圯YM=BC。由于YC=YC、YM=BC？圯Rt△YBC≌Rt△CMY？圯∠CYB=∠YCM？圯YA∥ZC？圯∠YAZ=∠CZA、∠D=∠AZC？圯∠YAZ=∠D

而△YOA和△ZOD中可以推出∠1=∠4？圯∠2=∠3？圯∠1+∠2=∠4+∠3？圯∠α=∠β？圯XY=XZ

∴△XYZ为等腰三角形

在上述论证中，证明了三角形两个外角平分线相等的情况下，此三角形为等腰三角形，这样的方法并不是唯一的论证方法，教师在展开教学活动中应从多个方面切入，注重的是培养学生的逻辑推理能力，而非固定的“论证方法”灌输，要注重培养学生的学习兴趣，从而激发和加强学生的逻辑推理能力。

三、关于三角形平分线的初中教学

在初中教学的“三角形角平分线”中，其内角平分线是指三角形中的一个内角的平分线与它的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线，但是，学生在学习的过程中，由于对几何的逻辑推理缺乏兴趣，常常没有很高的学习热情，也导致学生学习成绩无法有效提高，教师在教学工作中，应从以下几方面考虑：

在三角形外角平分线的教学中，可以结合多媒体技术向学生展示论证过程，多媒体技术可以将图片、文本、影视、声音和教学相结合，这种方式的应用能打破几何理论教学中的抽象性，通过营造一个拥有视听的立体化环境，把教学中无法通过教师讲解和分析表现出来的东西展示出立体可见画面。比如，在初中几何课堂中所讲解的三角形平分线一课中，用传统的讲解方法只能局限于理论讲解和论证分析，这样的讲解是概括抽象的，学生在学习的过程中由于思维缺乏对这具体现象的联系，对于教师的讲解，学生思维上只能发挥表层的“记忆”功能，无法对知识进行深入地分析和探究。因此，对多媒体技术的利用，可以需要论证的图形展示清楚，把整个论证过程用动态的方式展现出来，从而营造出一个理想的学习环境，让学生对初中几何的学习能力得到提高和巩固，这样的教学方法是让学生在几何的学习过程中提高自身的科学素养，在社会的生活中学会用科学的眼光分析科学性现象，符合素质教育的宗旨。

要理解三角形外角平分线的知识，在教学中应满足整个论证推理完整的前提下尽量简化论证的过程，可以让学生对复杂的论证方法进行简单的掌握，然后再由易入难。因此在运用这样的教育模式开展教学工作中，不应只局限于对教材的理论分析，可以让学生利用多媒体技术加深几何知识在社会生活中的实际运用。比如，学生在学习几何的课程中，三角形外角平分线相等为等腰三角形这些命题是谁发现的，在教材中并没有具体描述，因此，可以让学生通过互联网的平台去搜索相关知识，可以通过微博、论坛等渠道去发表对几何的评论，通过对几何的发展历程的研究，让学生利用多媒体技术去自主展开学习探讨，引导学生在学习过程中发现科学技术的人文精神，提高了辩证唯物主义教育的效果，能有效培养学生对几何的学习兴趣。

从教育改革的层面上看，多媒体技术结合的几何教学是一种未来教育的发展趋势，我们可以采用与多媒体技术相结合的教学方式去对学生进行更直观立体的教学，对于图形的论证可以产生详细的动态描绘，同时注重学生的逻辑能力培养，充分发挥学生自主学习能力的积极性，可以让学生在这样的教学中获得创新的动力，是培养学生创新能力的有效措施。

参考文献：

[1]王彦海.关于Steiner-Lehmes定理外等长分角线的猜想的研究[J].乌鲁木齐成人教育学院学报，2010（3）：82-85.

[2]洪盈平，崔树峰.斯坦纳定理推广猜想的证明及再讨论[J].安康师专学报，2010：93.

[3]敬坤.三论三角形外解平分线三角形的性质[J].数学教学通讯：上半月，2011（9）.

（作者单位 福建省莆田市莆田哲理中学）