数字式电流型降压变换器的建模研究

徐 振，赵 晨

(1.浙江机电职业技术学院 电气电子学院，浙江 杭州310053;2.杭州电子科技大学 自动化学院，浙江 杭州310018)

在DCDC变换器中，为获取较好的稳定性，电流型控制已超越电压型控制方式成为主流。电流型控制本质为双环控制，其内环为电流信息反馈，外环为电压信息反馈。采用电流型控制方式可以使得DCDC变化器系统的阶数降低，从而简化系统的补偿设计，获得较高的带宽。随着数字控制芯片的引入，数字控制芯片种类的逐渐增加。各大电源管理芯片厂商都在研究对应的数字控制芯片。早期的数字控制芯片主要采用电压型控制方式。近年来数字式电流型控制芯片得到广泛重视。文中重点分析了数字式电流型控制策略对系统环路的影响。并提出了系统的环路模型以及补偿控制中的注意事项。系统仿真与实验结果证明了数学模型的合理性。

1 数字电流型降压变换器原理与建模

1.1 电路结构分析

在降压型变换器的结构中，对电感电流和输出电压分别进行数字采样，将采样后的电流和电压信息输入到数字控制芯片，经过数字控制芯片内部的逻辑运算，输出占空比PWM信号，即为数字式电流型降压变换器的基本结构，如图1所示。为节省资源并降低硬件成本，通常会控制采样的速度。最常见的数字控制芯片中，电流和电压的采样速率均与开关速率相等，即在每个开关周期中对电流信息和电压信息各采样一次。

以定频率工作的降压电路为例，为避免采样到电感电流中的高频噪声，电流信息的采样点通常在开关动作之后一个固定的时间TD。而电感电流的获取可通过串联电阻采样，DCR采样或开关管电流采样等方式实现。电压信息的采样点可自行选择，但不同的采样点会对系统造成不同的影响。将采样到的电压信息与基准信号比较之后经过数字补偿环节得到补偿输出信号VCOMP，补偿输出信号与电流采样信号以一定的比例加权后和一个固定的数字斜坡信号比较可得到PWM输出信号。

1.2 电流环路模型分析

在图1中，首先关注电流反馈环路。与模拟电流型控制方法类似，电流环路由于带宽较高，用平均模型进行分析通常会在高频段造成误差，并丢失可能出现的次谐波振荡等信息［1］。因此在具有电流反馈回路的结构中，通常可将电流环路当作一个整体，直接分析电压环路补偿电路的输出控制信号与电感电流之间的关系。分析电感电流的自然响应［2］，如图2所示。

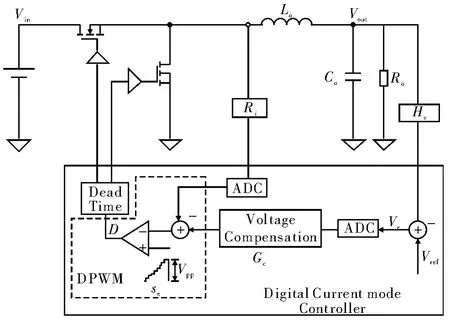
图1 数字式电流型降压变换器

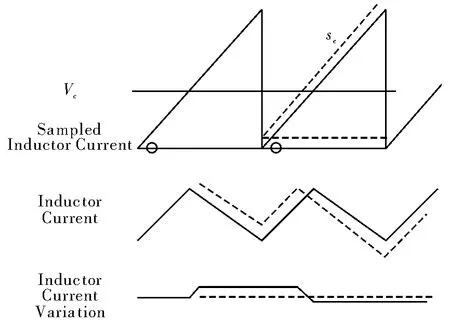
图2 电感电流自然响应

与模拟式的电流型控制相比，电感电流的变化周期为，从本周期上管关断时间到下周期上管关断时间。根据图3中的时域关系，当本周期电感电流变化为L(n)时，

则下周期占空比变化为

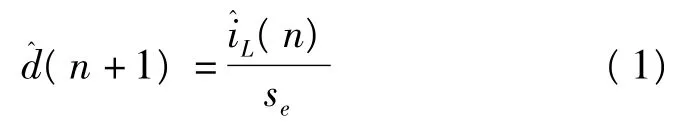
下周期电感电流变化为

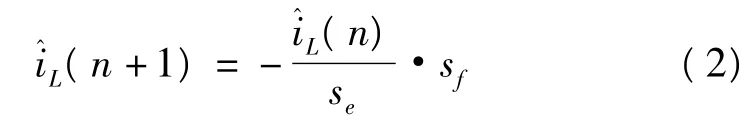
从图3分析中可知，只有占空比的变化会影响下周期电感电流的变化，电流采样点的位置并不影响电感电流的自然响应。式(2)中，如果se＜sf，则电感电流的扰动呈现增大趋势，系统不稳定。

当控制信号受到扰动时，如图4所示可以分析电感电流的受迫响应。

本周期占空比的变化为

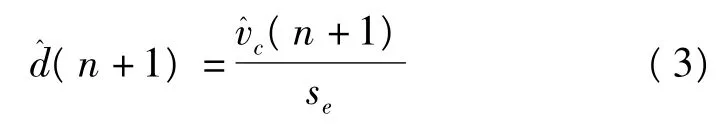
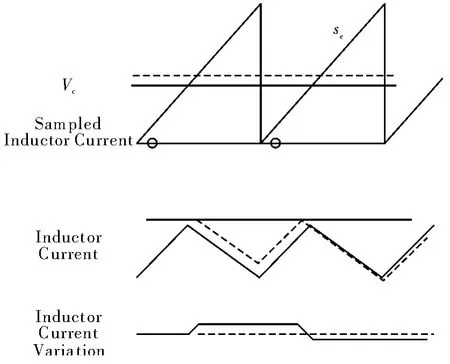
图3 电感电流受迫响应

电感电流的变化为

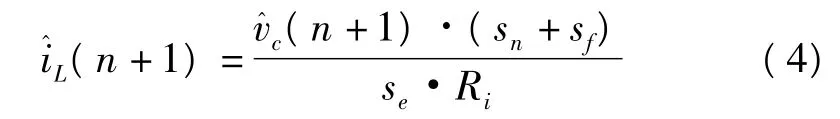
其中，电流采样系数为Ri。在以上分析中，电感电流的变化也与采样点的位置无关。

综合电感电流的自然响应和受迫响应，可得到电感电流扰动的时域表达式

依据此表达式可得电感电流与控制信号离散域的传递函数为

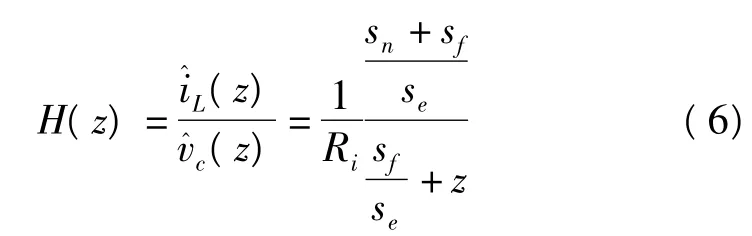
根据采样保持系统的离散z域与连续s域之间的转换关系［3］

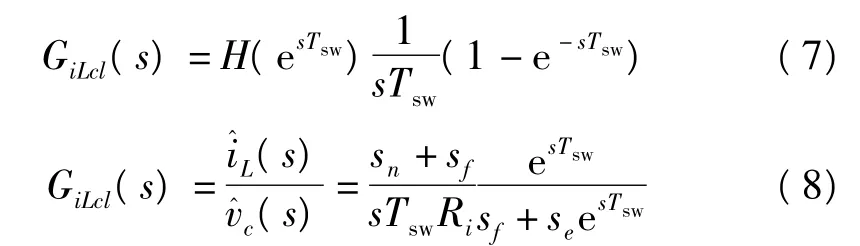
数字式电流型降压变换器控制信号与电感电流的传递函数小信号表现为受控电流源，其中斜坡信号的斜率直接决定了电流环路的稳定性。较小的斜率会造成系统次谐波振荡，较大的斜率会使得电流环路在关心的频段范围如1/10 Fsw～1/3 Fsw之间产生过多的相位跌落。值得注意的是电流采样点的位置并不影响电流环路的模型。

1.3 电压环路模型分析

在得到电流内环闭合的传递函数之后，可以进一步分析电压环路的模型，从而分析电压环路补偿的设计依据并分析影响系统稳定性的因素。

在电流内环的分析中，已将电流内环和主电路看作一个整体，得到从控制信号到电感电流的传递函数。即可进一步分析图1所示的电压环路中其他模块的传递函数，从而得到整个环路的模型。

电感电流到输出电压的传递函数为线性输出负载阻容网络。根据线性网络分析

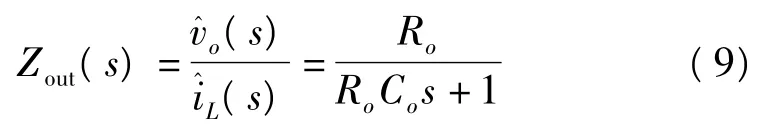
电压采样传递函数记作Hv。Hv可以是单纯的电阻分压网络，也可是阻容的网络。

假定电压采样点为时钟信号之后延迟一个固定时间TD1。在电压环路中，电压采样的信息要经过系统的补偿环节，因此不同的采样点会带来不同的系统延时，系统延时为信息的采样点与该信息用于决定占空比的时间点之间的时间间隔［4］，如图4所示。

图4 电压采样与系统延时较小的情况

在关断沿调制的变换器中，占空比的结束时刻是所有采样信息的使用时刻。图5中，电压采样点在本周期时钟信号之后且在占空比关断沿之前。假定数字控制器内部的所有延时包括ADC的转化时间，补偿信号的计算时间之和较小，从而使得本周期的电压采样信号可用于本周期的关断沿调制，则系统的延时时间较少。

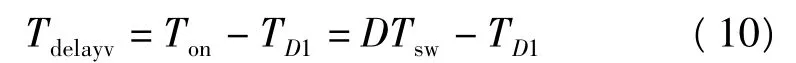
当计算出电压补偿的信号晚于本周期的上管关断时间时，则本周期计算出的电压补偿信号用于判断下周期占空比关断沿调制，系统延时增加。如图5所示。

在这种情况下，系统的延时为

因此在电压环路中，根据系统内部固有延时和系统占空比，合理选择电压采样点可以使得系统的延时减小。

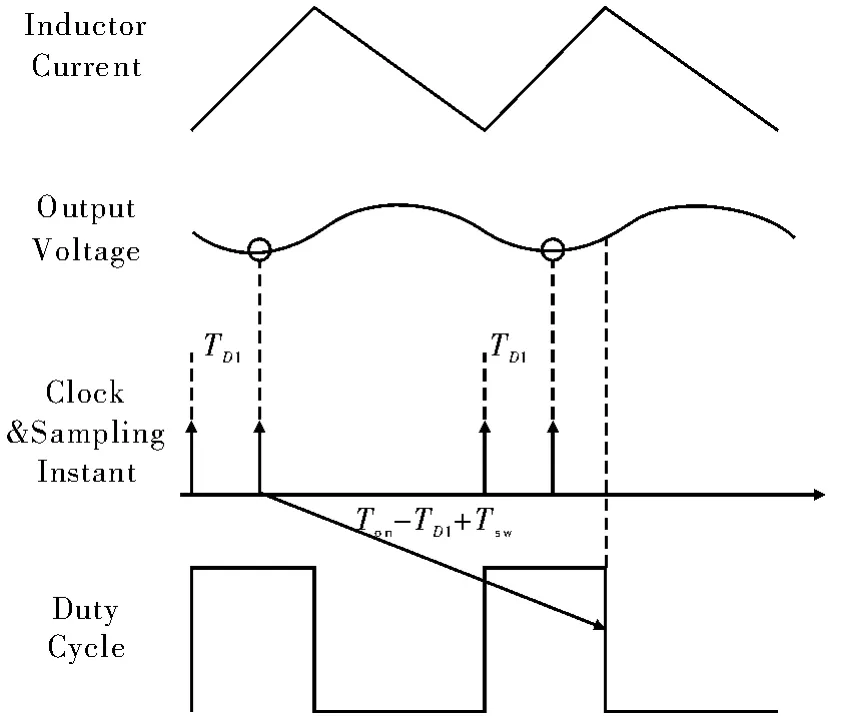
图5 电压采样与系统延时较大的情况

在数字芯片中的环路补偿是用数字算法实现的，常见的可以采用数字的PID补偿。由于电源工程师通常习惯于模拟的补偿概念，在实际补偿中可先按照模拟电路的补偿方式设计补偿传递函数Gc。然后将模拟s域的传递函数映射到离散z域，并得到差分的表达式。在系统关心的频段范围内，仍可用模拟传递函数Gc来分析环路特性，并简化系统的分析。

综合以上电压环路各个模块的分析，系统环路的模型结构如图6所示。

图6 系统环路模型

系统环路传递函数为

1.4 系统模型分析

整个系统的传递函数分析中，电流内环的闭合使系统在较低频段体现出电流源的特性，从而降低了系统的阶数，应合理选择斜坡信号的斜率从而保证电流内环的稳定性。电感电流的采样点不影响小信号的模型及电流内环的稳定性。

在电压外环中，系统采样带来的延时相比于模拟的系统而言引入了更多的相位跌落，从而使得系统的稳态裕量降低。应结合不同采样系统硬件的速度合理选取电压采样点的位置从而将系统的延时降低。

有了系统的环路模型，可以依据此模型对系统环路进行补偿，从而在有合理、稳定裕量的情况下尽可能地加快系统的动态响应。

2 仿真与实验验证

2.1 仿真验证

为验证上述小信号模型的合理性，利用仿真软件Simplis搭建了仿真电路。其中仿真参数为:输入电压Vin=5 V，输出电压Vo=1.2 V，开关频率Fsw=500 kHz，电感Lo=4.7μH，输出电容Co=22μF，负载Ro=1.2Ω。电感电流与输出电压每周期均采样一次，电感电流采样系数Ri=100 mΩ，斜坡信号斜率为se=1 V/Tsw，其中TD=100 ns。

在仿真实例中选取的补偿结构为

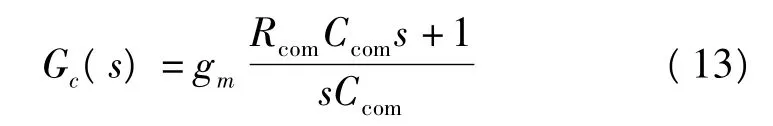
其中，gm=5μs，Rcom=300 kΩ，Ccom=30 pF。补偿器由积分环节和比例环节构成。电压采样点在时钟信号后200 ns，则系统延时仅为280 ns。系统环路传递函数与仿真的比较如图7所示。

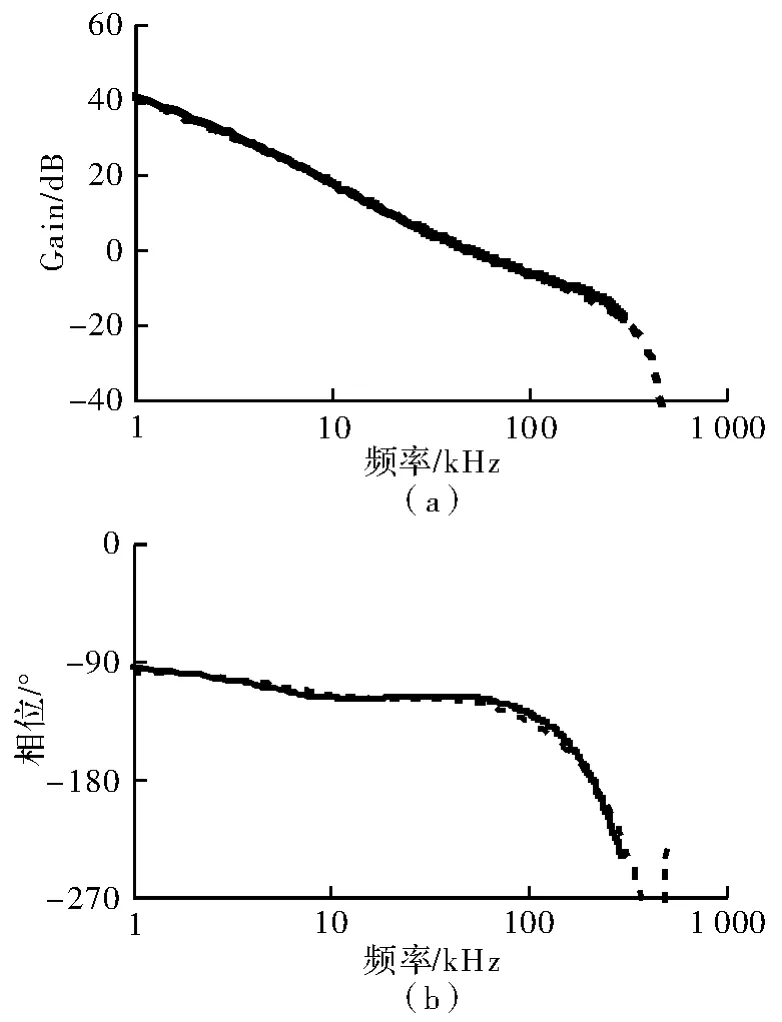
图7 系统仿真与模型的比较(TD1=200 ns)

在图7中，实线为根据式(12)计算出来的模型，虚线为仿真结果。系统带宽为50 kHz，相位裕量为59°。

如果将采样点后移到时钟信号之后600 ns，则根据式(11)可知系统延时为1.88μs。在同样的50 kHz系统带宽时，系统的相位裕量仅为27°，如图8所示。由此可见电压采样点的选取对系统稳定性的影响。

2.2 实验验证

图8 系统仿真与模型的比较(TD1=600 ns)

利用Altera公司型号为EP2C8Q208的FPGA搭建数字控制平台，其中DPWM利用系统高频时钟加延时线的方式实现，从而提高了DPWM的分辨率。电感电流和输出电压采样采用Analog Devices公司的AD7484。当采样点为时钟信号后200 ns时，实验结果如图9所示。当采样点为时钟信号后600 ns时，实验结果如图10所示。其中上方波形为输出电压，下方波形为电感电流，负载电流均由1 A跳变至2 A。

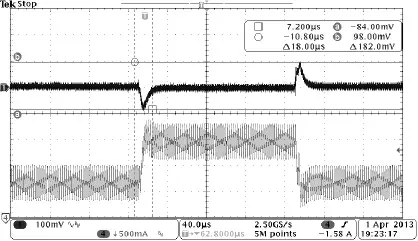
图9 输出负载跳变(TD1=200 ns)

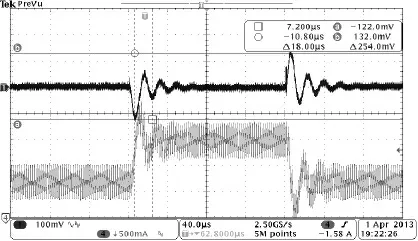
图10 输出负载跳变(TD1=600 ns)

比较图9和图10中不同的输出电压暂态响应，可以看出不同的采样点造成的系统延时的差异对系统稳态裕量的影响，从而验证了上述模型的正确性。

3 结束语

文中对数字式电流型降压变化器的模型进行了分析。该数学模型指出合理的斜坡补偿可以使得电流环路稳定并得到受控电流源。电压采样点会决定系统的延时，在数字系统中，应保证采样信息在最短的时间内得到使用。仿真和实验的频域、时域结果都较好的验证了数学模型的合理性。

［1］MIDDLEBROOK R D.Modeling current programmed buck and boost regulators［J］.IEEE Transaction on Power Electronic，1989(4):36－52.

［2］RIDLEY R B.A new continuous－time model for currentmode control with constant frequency，constant on－time，and constant off－time［C］.CCM and DCM，in proceeding IEEE PESC'90，1990:382－389.

［3］GENE F，FRANKLIN J，DAVID P，et al.Digital control of dynamic systems［M］.CA:Ellis－Kagle Press，2006.

［4］VAN de SYPE D M.Small－signal Laplace－domain analysis of uniformly sampled pulse－width modulators［C］.Salt lake:In PESC 2004，IEEE 35th Annual，2004.