基于LabVIEW的混沌微弱信号检测系统设计

2013-04-25司淑平

电子科技 2013年6期

司淑平

(中国电子科技集团公司第8研究所，安徽淮南232001)

混沌理论用于微弱信号检测是新的研究领域。至今已报道的关于混沌用于微弱信号检测的方法，主要都是利用混沌对周期信号的敏感性和对噪声信号的强免疫力，构造处于混沌状态的非线性系统，实现高精度测量。基于混沌理论检测信号的理念是:对于一个非线性动力系统，其参数的摄动有时会引起周期解发生本质的变化。将待测信号作为混沌系统特定参数的摄动而引入该系统，利用混沌系统丰富的非线性动力学特点，如倍周期分叉、奇怪吸引子等特点，通过辨识系统所处的运动状态，根据系统从混沌到有序和从有序向混沌的相变可判断有无待测微弱信号的出现，再通过调整系统的参数实现对微弱信号的测量［1－4］。

判别系统是否处于混沌状态有多种方法。定量分析法中的Lyapunov指数法误差小、可精确地辨识系统从混沌态向周期态的跃变，消除了时间历程法和相轨迹法等直观方法可能出现的误判情况，具有较高的判断精确性，成为一种重要的判别工具。

LabVIEW是美国NI公司推出的一种基于编译型图形化编程语言的虚拟仪器软件开发平台，其主要特点是支持多种标准总线和接口，如PCI、GPIB、PXI、RS－232、RS－422/485、USB等，便于实现数据交互;但计算精度不足。Matlab具有数据计算处理能力强、数值计算精度高、编程简单等特点。将Matlab计算模块嵌入到LabVIEW平台中，从而实现两者优势的结合［5］。文中首次提出了将混沌微弱信号检测系统建立在LabVIEW平台下，结合Matlab高精度计算的优点，有利于信号检测后进一步的硬件处理。在该平台下利用Lyapunov指数法计算系统由临界状态到大尺度周期状态变化的临界值。

1 Lyapunov指数法判别混沌状态

在周期外力作用下Holmes型的Duffing方程为

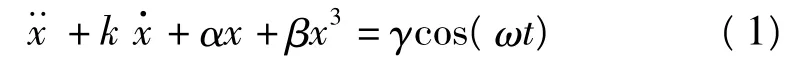
式中，k为阻尼比;αx+βx3为非线性恢复力;γ和ω分别为周期摄动力的幅度、频率;α、β为实数因子;取α，β分别为－1和1，k=0.5。该系统方程变为

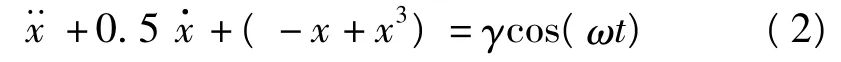
利用Lyapunov特性指数判别混沌的标准是:只要存在一个正的Lyapunov特性指数，则说明系统处于混沌态。最大Lyapunov特性指数＞0，是系统处于混沌状态的必要条件，而最大Lyapunov特性指数＜0，则说明系统处于大尺度周期状态［6］。

对于Lyapunov指数的求解，常用的有QR分解法、RHR算法和改进的RHR算法［7］。在此基于改进RHR算法进行Lyapunov指数的求解。根据该算法的原理，编制了计算Lyapunov指数的Matlab程序。将其调入LabVIEW检测系统中，用于微弱正弦信号的检测。

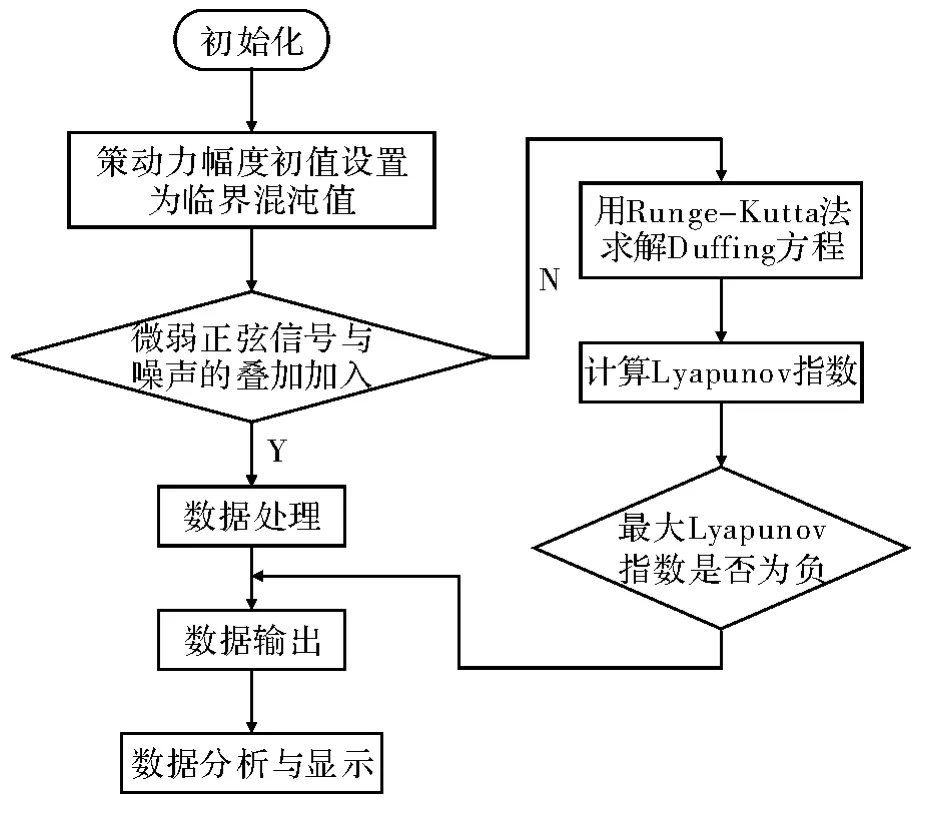
图1 检测流程图

通过相轨迹法判断系统处于临界混沌状态的策动力幅度。将系统设置在临界混沌状态，随后加入微弱正弦信号和噪声的叠加。计算系统的Lyapunov指数，通过最大Lyapunov是否＜0，判断微弱正弦信号的存在。

2 Lyapunov指数法微弱信号检测系统

2.1 混沌检测系统前面板部分

如图2所示，前面板上的控件部分为生成各种噪声与周期信号相叠加的信号发生器，作为微弱信号检测系统的信号源。该系统前面板有4个通道，每一通道分别有一个布尔性的开关通道选择。各通道分别用枚举类型设计，得到18种类型的信号噪声叠加。图中部的两个显示控件用于显示每次仿真所得到的两个Lyapunov指数的最终值。

图2 信号检测系统前面板图

图2所示，右上角示波器为系统相空间显示;右中示波器为Lyapunov指数1，Lce1随时间的变化曲线;右下Lyapunov指数2，Lce2随时间的变化曲线;左下方示波器为加入的微弱正弦信号;正下方示波器为所加入噪声的时间序列。

2.2 混沌检测系统程序面板设计

该检测程序在LabVIEW下程序面板显示如图3所示，噪声与信号叠加部分未显示。

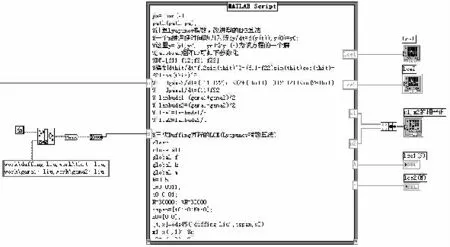
图3 Matlab Script接口检测程序面板图

在程序面板中，执行Function＞＞Mathematics＞＞Formula＞＞Matlab Script操作［8－10］，调入LabVIEW和Matlab的结点。在结点内右击鼠标，选择Import，调入求解Lyapunov指数的主程序。并在调入程序的前写入pa=char(s);path(path，pa);

在程序面板内执行Function＞＞File I/O＞＞File Constant＞＞Default Directory操作，调入当前LabVIEW文件的默认目录。

执行Function＞＞String＞＞String Constant操作，产生信号的文件名及路径设置图标，在图标中填入程序文件相应的路径和文件名。

在Matlab Script左边框上，单击右键，操作Add Input两次，分别命名为m和s。其中m指的是湮没于噪声中的微弱信号。而s则是路径名称。

在程序面板的Matlab Script右边框上，单击右键，操作Add Output 6次。分别命名为:lce1、lce2、x1、x2、lce1(N)和lce2(N)，作为从Matlab中输出的两个Lyapunov指数、两个状态变量和Lyapunov指数的最终值，并分别连接显示模块。