高频电磁防护织物屏蔽效能研究

胡卫东，李 萍，彭 煜

(1.武警工程大学 研究生大队，陕西 西安710086;2.武警工程大学 信息工程系，陕西 西安710086)

所谓电磁屏蔽就是以某种导电或导磁材料制成实体的或非实体的屏蔽壳体，通过这种壳体将需要屏蔽的区域封闭起来，形成电磁隔离，即内部电磁场不能越出这一区域，而外来辐射电磁场不能进入这一区域或进出该区域的电磁能量将受到大幅衰减［1］。考虑到使用金属板材屏蔽体的成本高、加工工艺难度高以及对屏蔽体便携性的要求等，在屏蔽要求不十分精密的情况下，通常用金属栅极或金属网格替代金属板进行电磁屏蔽。

近年来，非致命性微波武器的优势逐渐显现。凭借杀伤率低的特点，非致命性微波武器填补了传统致命性武器在处置突发事件中的局限性。国内外学者不断地探讨各种吸波材料，就战地复杂的电磁环境所进行的防护标准研究也是凤毛麟角。针对30 GHz以上频段的电磁防护研究更是少之又少，而且大多集中在设备的防护方面。

1 电磁防护织物模型建立

频率选择表面是一种二维周期性金属谐振单元阵列结构，织物本身具有网状的结构特性，因而可以将防护织物简化为网状结构来构建等效模型。而在研究网状织物的屏蔽效能时，无非是改变网格的结构形状，本文运用电磁仿真软件Hobbies软件建立了金属网格结构，并找出影响网格结构的几个参数:网格中单元四边形的边长l;金属丝半径d;四边形的顶角θ。

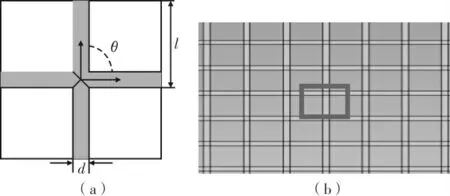
图1 织物结构等效模型

Hobbies软件使通用的电磁仿真软件，能够高精度求解超大规模电磁模型，解决电磁散射、辐射、电磁兼容等问题。

2 网格结构参数对屏蔽效能的影响

2.1 屏蔽效能的表示

屏蔽效能SE，其定义为屏蔽前某点的场强与屏蔽后该点场强之比。用公式表示为

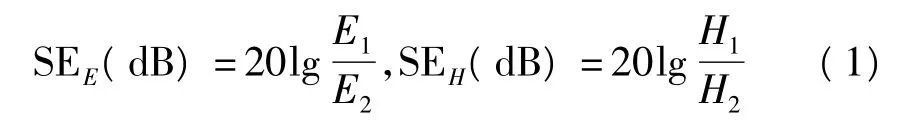
式中，E1是入射电场强度(V/m);H1是入射磁场强度(A/m);E2是屏蔽另一面电场强度(V/m);H2是屏蔽另一面辐射出磁场强度(A/m)［2］。

2.2 仿真分析

经过仿真发现:平面波入射角度φ越大，防辐射服对电磁波的衰减也就越大。因此，只需讨论平面波垂直入射时的情况，如果这种情况满足，那么斜入射时的性能指标便自然满足，以下研究的是均为平面波垂直入射的情况，并且考察频点选在90 GHz。由于等效金属网格结构是一个典型的高通FSS结构，如果在90 GHz频点处的屏蔽效能满足要求，那么由此就可断定已经达到了相应的性能指标。仿真结果如表1所示。

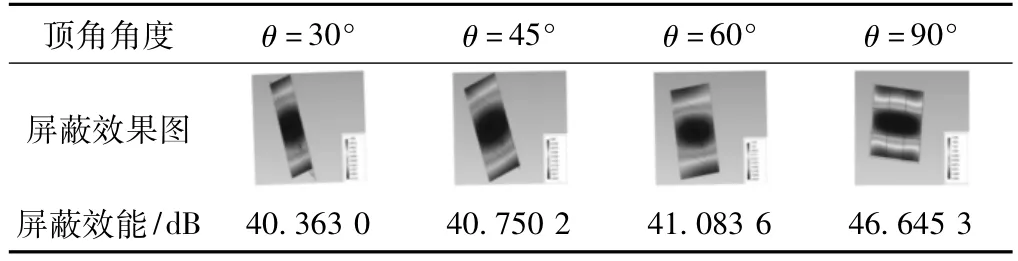
表1 不同顶角的四边形网孔结构模型的屏蔽效能

如表1所示，四边形的顶角θ越偏离90°，深蓝色区域所占的面积越小，整体的屏蔽效能就越低，顶角θ取90°时的屏蔽效果最佳。

表2 屏蔽效能与单元四边形(孔径)之间的关系

如表2所示，4组尺寸模型的屏蔽效能相差不大，电磁波的衰减程度均达到了中等水平。随着孔径的减小，模型的屏蔽效能也略有降低，因此孔径以不超过2μm为宜［3］。

表3 屏蔽效能与金属丝半径之间的关系

如表3所示，屏蔽效能与金属丝直径成反比;可以推论:采用直径＜20μm的金属纤维纱线进行纺制，织物的屏蔽效能均在46 dB以上。根据上述分析得知，模型的孔径越大、线径越小，整体的屏蔽效能就越大。

2.3 尖劈效应对屏蔽效果的影响

l与d取值边界处的模型屏蔽效果如图2所示，l=2μm，d=4μm时的屏蔽效果没有，l=0.5μm，d=20μm时的结果好，但按上述分析的结论，第二组的屏蔽效果应优于第一组。通过对模型的检查与分析发现，模型的横截面会出现如图3所示尖劈的结构，影响尖劈形吸波体对电磁波的吸收与反射作用的因素主要是尖劈的顶角α和长度h［4］。

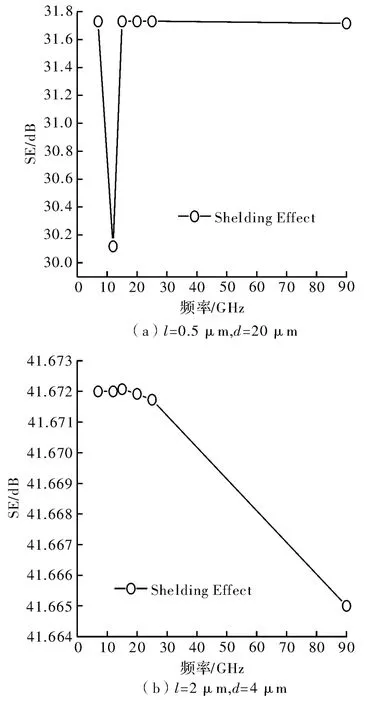
图2 与取值边界处屏蔽效能与频率的变化关系

当电磁波朝尖劈基底面垂直入射时，相邻两劈间的反射次数N为90°/α。而频率主要影响吸波体对电磁波的吸收效率，普通尖劈形吸波体长度与电磁波波长的近似关系为L/λ≈1［5］。可见，尖劈顶角越小，电磁波被反射的次数越多;频率越高，对应吸收率最高的尖劈长度越小。

在图3所示的单层屏蔽模型中，金属丝直径主要影响尖劈结构的顶角角度，金属丝直径越大，对应尖劈的顶角越小;网孔直径主要影响尖劈结构的长度，孔径越大，尖劈的长度越小。随着孔径的增大，尖劈结构对电磁波的最佳吸收频点会相应提高。

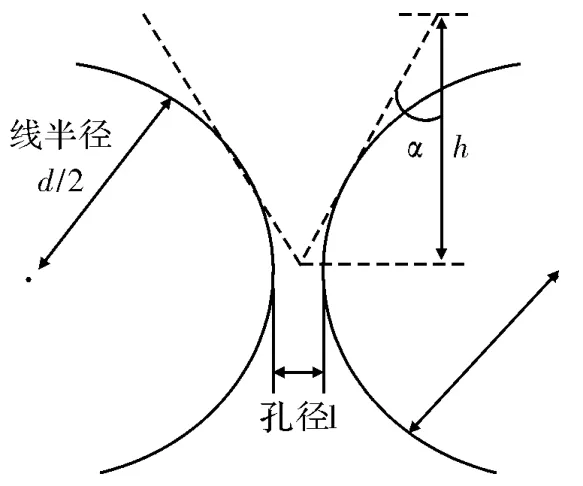
图3 单层织物的纵向剖面图

如图4(a)所示，电磁波会在尖劈之间发生多次反射;如图4(b)和图4(c)所示，线径的减小虽然会导致尖劈结构对电磁波的反射次数减少，但顶角度数的增大则会使尖劈结构的暴露面积增加。这会使尖劈顶端对反射波的阻挡作用减弱，从而增强屏蔽织物的屏蔽效能。因此可以推论:当金属丝直径大小是孔径尺寸的10倍以上时，由于尖劈结构的影响，当增加线径时，电磁屏蔽效能会下降。

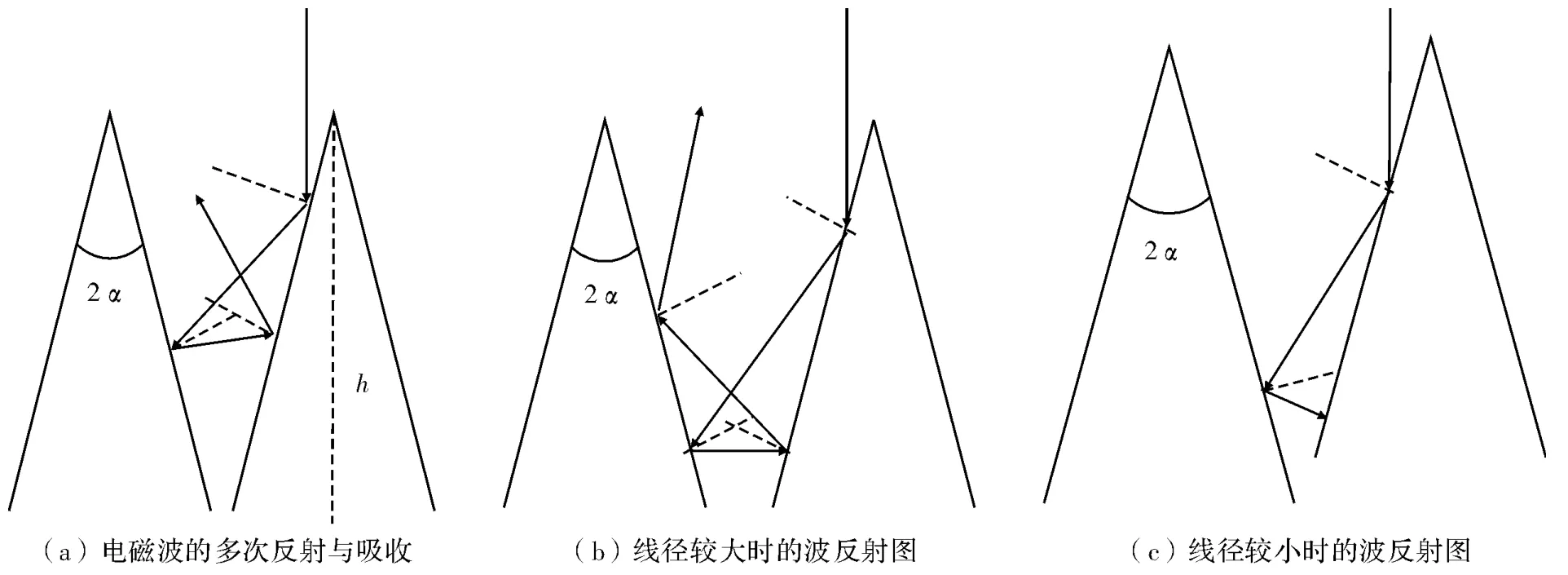
图4 尖劈形吸波体示意图

2.4 公式估算及其与仿真结果比对分析

根据Babinet原则［6］，一个狭窄槽的作用相当于一个细线偶极子，当槽的长度等于半波长时，辐射达到最大，即屏蔽效果最弱。当槽长度d等于或小于半波长时，SE值近似等于

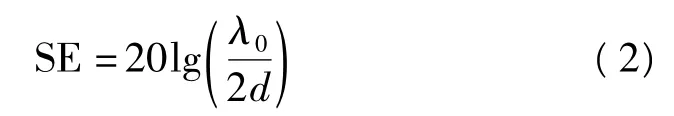
即SE值的减小与孔缝数量N的平方根近似`成正比。因此，从式(2)可知，SE与N个长度为d的槽有关，它可以通过式(3)进行计算

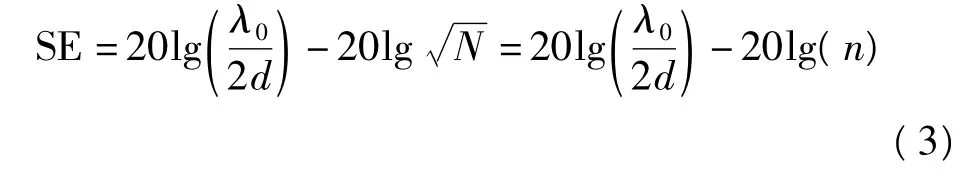
运用Matlab进行编程计算，结果如图5所示。可以发现:整体趋势是与l成反比但与d成正比。运用仿真和估算方法，分别得到了单层织物对90 GHz电磁波的屏蔽效能值，仿真结果比估算的好，孔径、线径分别取2μm和4μm时，如图6所示，模型的仿真结果与估算公式的计算结果走向一致，屏蔽效能都随着频率的升高而降低。

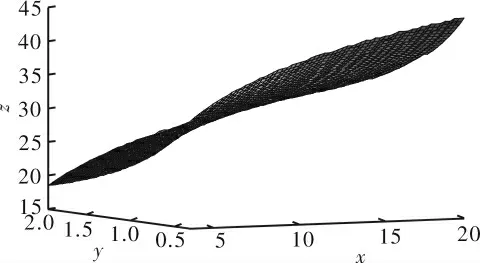
图5 经验公式对SE的估算结果

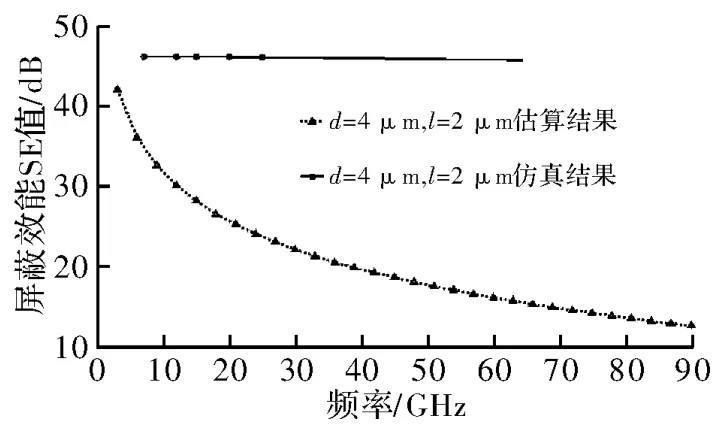
图6 l=2μm，d=4μm时估算和仿真结果对比

综上可知，当线径d与孔径l的尺寸之比设置到10倍以上时，屏蔽效能与孔径、线径的变化关系呈现反结果，因此传统的分析方法不再适用，而应采用尖劈形吸波体的相关理论进行研究［7］。当孔径与线径的尺寸相比拟时，仿真与估算结果走向一致，符合屏蔽效能的传统分析方法。

3 结束语

结合电磁防护的相关理论，采用微波仿真软件Hobbies对电磁波防护服饰基本结构的金属网格的各个参数进行了细致地仿真，给出了优化金属网格防护效能的结构与参数:四边形网格结构的顶角θ越偏离90°，整体的屏蔽效能就越低，孔径不超过2μm，直径＜20μm的金属纤维纱线进行纺制，织物的屏蔽效能均在46 dB以上。根据上述分析得知，模型的孔径越大、线径越小，整体的屏蔽效能就越大，但当金属丝直径大小是孔径尺寸的10倍以上时，由于尖劈结构的影响，当增加线径时，电磁屏蔽效能会下降。

［1］ 刁振河.高功率微波防护的相关问题［D］.湘潭:湖南科技大学，2006.

［2］ 石慧宇，李萍，马莹.高强度电磁辐射对人体产生的危害及有效防护［J］.中国新技术新产品，2010(23):25－28.

［3］ 韩钟剑.编织结构形式对网状反射面天线电性能的影响分析［D］.西安:西安电子科技大学，2010.

［4］ 吴大伟.电磁波吸波体及其在航空技术中的应用［J］.航空学报，1980(2):79－88.

［5］ 林红磊，王怡然，胡英男.尖劈吸波体和微波暗室中的数学建模［J］.数学的实践与认识，2012(7):162－174.

［6］SALVATORE C，RODOLFO A.电磁屏蔽原理与应用［M］.郎为民，姜斌，译.北京:机械工业出版社，2009.

［7］PHILIPPAKIS M，MARTEL C，KEMP D，et al.Application of FSS structure to selectively control the propagation of signals into and out of buildings［R］.U K:ERA Technology Limitted，2004.