针对发音质量评测的声学模型优化算法
2013-04-23戴礼荣
严 可,魏 思,戴礼荣
(1. 中国科学技术大学,安徽 合肥 230027; 2. 科大讯飞股份有限公司,安徽 合肥 230088)
1 引言
随着计算机科学与信息科学的发展,计算机辅助学习系统(Computer Assisted Language Learning, CALL)走进千家万户,发挥着日益重要的作用。发音质量评测是计算机辅助学习的重要内容,它不仅能显著提升口语学习效率,还可代替教师进行口语考试部分题型的评分,极大缓解了大规模机考实践中教师评分任务繁重及费用居高不下的问题。目前,在文本相关的发音质量评测任务上,如朗读、跟读等,计算机已经接近人工评分水平[1],并在普通话水平测试、英语学习等任务上得到广泛应用,但性能仍需改进。
本文研究属于文本相关的评测,即考生按照指定文本发音,计算机根据发音质量反馈出分数。一般采用自动语音识别(Automatic Speech Recognition,ASR)技术,根据给定文本将语音切分到音素,在此基础上计算能反映发音标准度和流畅度的评分特征,进而给出机器分。在常用的评分特征中,帧规整后验概率[2-3]是目前公认的最能反映发音标准度的度量。另外,人们常用的GOP (Goodness of Pronunciation)算法[4-5]也是在帧规整后验概率理论框架下的简化。
声学模型是帧规整后验概率计算的重要依据。由于自动发音质量评测的研究源于语音识别,至今人们仍普遍采用语音识别技术进行声学建模。但语音识别与发音质量评测有着显著不同: 语音识别需要包容非标准发音,因此采用标准发音和非标准发音混合训练声学模型,能使训练与测试更加匹配,从而有效提升识别性能;而发音质量评测任务需严格鉴别标准发音与非标准发音,因此人们仅使用标准发音进行声学建模。
起初,人们自然想到使用公认的最为标准的发音——第一语言学习者(L1)的标准发音进行声学建模[2]。但随后发现这种方式会给第二语言学习者(L2)相似的分数,无论其发音是否良好。显然,这是由于L2与L1的发音风格差别很大导致。于是,人们提出采用良好的L2发音来进行声学建模[6]。虽然这种建模方式在L2的学习任务上性能良好,随后发现机器会给L1较低的分数。因为该建模方式认为良好的L2发音才是“标准模版”,而标准的L1发音与之相去甚远。不难预见,若L1的标准发音和L2的良好均参与声学模型训练,系统必然会认为这两种发音同样标准(而显然L1应更标准),这种情况同样令人尴尬。
如何将非标准发音融入声学建模,人们进行了不懈努力。文献[7]提出了“发音空间建模”思想,将声学模型分为“标准发音”、“中等发音”和“差等发音”;文献[8]利用语音识别区分性训练框架,同时使用正确发音和错误发音数据进行声学模型优化。虽然上述策略提升了系统检错性能,但上述方法应用于发音质量评测时,需要人工音素级分数,不仅标注量强度大,且标注质量无法保证。
本文提出一种全新的针对发音质量评测任务的声学模型的优化算法。该算法通过最小化训练集机器分与人工分均方误差准则,同时利用覆盖各种发音的数据优化声学模型,从根本上解决了传统方式建立的声学模型对非标准发音视而不见的问题,且不需音素级人工标注。同时,声学模型的优化通过调整均值和方差进行,不改变模型结构,不会增加评测算法的时间复杂度。另外,该算法与评测常用的后验概率理论紧密相联,可与各种最新的研究成果融合。实验在3 685份普通话水平现场考试数据集上进行(498份用于测试,3 187份用于训练),并研究该算法在最新的一些研究成果下的性能。实验结果均表明该优化算法得到的评测声学模型相比传统方法所得到的声学模型均有着显著的优势。
2 发音质量评测系统介绍
自动发音评测系统一般是在语音识别的基础上,提取能描述发音质量的评分特征,再结合评分模型计算得到分数。常用的评分特征有帧规整后验概率、语速、时长得分等。其中帧规整后验概率是目前公认的最能反映考生发音标准度的评测指标;语速和时长得分等特征反映了发音的流畅度[2,9]。
令音素集共包含I个音素,对于其中第i个音素,采用隐马尔可夫模型(HMM)描述其声学特征,记为θi,则音素集可表示为θ={θi},i=1,2,…,I。对于一篇含有N个音素的朗读文本,可表示为Text=(θid(0),θid(1),…,θid(N)),其中id(n)为文本中第n个音素的序号(下文用j表示,即j=id(n))。将文本与语音进行对齐(Forced Alignment)后,得到其对应的观测矢量序列On和时(帧)长Tn。于是音素级发音标准度的度量——帧规整音素后验概率(通常以对数形式表示)的计算如式(1)所示,其中Q为全音素概率空间[1]。
篇章级发音标准度为音素度量的平均,如式(2)所示:
语速(ROS)和时长分(Duration Score)是常用的描述发音流畅度的指标。其中语速的计算如式(3)所示。
时长得分的计算需要先在训练集统计各不同音素时长的均值和标准差,记为{μi,σi}。于是,时长得分的计算如式(4)所示。
在得到上述评分特征后,最终机器分可通过如式(5)所示的线性评分模型得到,模型参数w,b通过在有人工评分标注的数据上训练得到,其中x=(MR,ROS,Dur)T为评分特征。
评分模型也可采用非线性的形式[1,10],但性能仅有小幅提升。可以看到,人工标注的数据仅参与只有少量参数的评分模型的训练,其作用未得到充分发挥。
3 普通话水平测试系统中帧规整后验概率策略的改进
普通话水平测试是L1的发音水平测试,由于L1普遍发音流畅,按大纲要求,发音标准度是其重点考察内容,因此帧规整后验概率的性能直接决定了系统性能。近年来,如何使帧规整后验概率能更好地描述考生发音标准度,人们进行了不懈努力。
3.1 基于语音识别技术的改进
该策略的主要思路是建立更精确且更易区分的声学特征或者声学模型。在声学特征方面,文献[11]利用HLDA去除声学特征中冗余信息,提升了声学特征的区分性;文献[12]研究了在根据区分性思路提取的TANDEM特征,均取得了一定收益。在声学模型方面,文献[12-13]考察了区分性训练[14]在发音质量评测任务上的应用,取得了一定的收益。
3.2 帧规整后验概率的概率空间的改进
然而,式(1)所示的帧规整后验概率不仅反映了考生的发音标准度,还反映了当前发音所对应的声学模型与概率空间中声学模型的混淆,从而严重影响了评分性能。于是文献[10,15-16]通过优化概率空间的方式,减少了混淆,已成为目前普通话水平测试的标准配置。实现方式如式(6)所示,其中Qi为音素集中第i个音素所对应的概率空间。
文献[15]通过普通话水平考试现场数据的典型错误总结出概率空间,侧重对发音错误(错发成音素集中另一音素)的评测;文献[10](第22-27页)通过KLD聚类得到概率空间,侧重对发音缺陷(发音不像音素集中任何音素)的评测。两者性能相对于式(1)的全概率空间均有显著的提升。
3.3 帧规整后验概率的变换作为发音质量的度量
文献[17]提出的“音素评分模型”可视为是音素相关的后验概率变换,通过对人工分的学习使得不同音素的在变换后的帧规整后验概率更好地反映发音标准度,如式(7)所示。
其中变换参数{αi,βi},i=1,2,…,I在有人工评分的数据集上通过最小化机器分与人工分的均方误差得到。同时,文献[17]还提出了更接近评分员主观评测准则的非线性sigmoid变换,但性能只有微弱提升。
4 针对发音质量评测的声学模型优化
本节将详细介绍针对发音质量评测的声学模型优化算法。同时该算法与评测的帧规整后验概率理论框架紧密相联,可轻松与上节回顾的改进策略相融合,进一步提升系统性能。
4.1 数据库的表示及与传统建模方式的区别
令声学模型训练(声学模型的优化属于声学模型的训练或声学建模的过程)数据库包含R段语料,对于其中第r(r=1,2,…,R)段语料,对应的观测矢量为Or,参考文本为Wr,人工评分为sr,则数据库可写成如下形式:
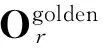
可见,本文提出的建模方式与传统的发音质量评测的建模方式差异显著。首先,人工分及朗读文本均是声学模型优化的重要依据;其次,标准发音、非标准发音、甚至错误发音均可参与声学模型的优化;同时算法不需要精细到音素级的人工评分,仅需要篇章级分数。
4.2 声学模型优化准则——最小化机器分与人工分均方误差

注意ROS,Dur是根据语音识别结果提取的评分特征,与本文的声学模型更新无直接关系。本文仅考虑如式(1)、式(2)所示的传统的后验概率策略和式(5)的线性融合方式,即假设机器分为式(2)所示的篇章级度量的线性变换,如式(11)所示。
其中a,b为线性回归模型的参数,j=id(r,n)为第r段语料的文本中的第n个音素的序号(下同)。将式(1)和式(11)代入式(10),于是目标函数如式(12)所示,参数a,b通过线性回归得到。
4.3 声学模型的参数优化
声学模型参数θ在固定a,b基础上进行。将目标函数对第i个声学模型的第s状态第k个高斯(记为θisk)求偏导,有:

Aux(Or,n,θ)

(14)
辅助函数与原函数在原点相切[14],简化了式(13)的偏导计算。
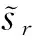
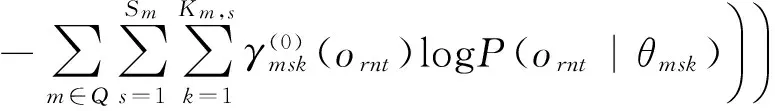
(16)
将辅助函数S(θ,θ(0))按高斯合并同类项,如式(17)、(18)所示。
其中
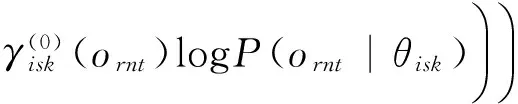
(18)
为加以简洁的描述,仿照文献[20]引入统计量的概念,如式(19)所示。统计量可以直接根据更新前的模型θ(0)求得。
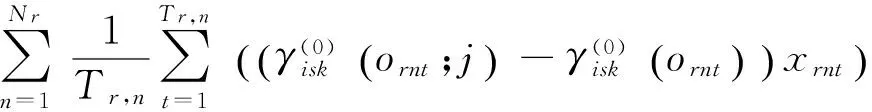
(19)

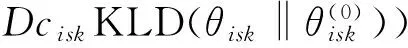
(21)
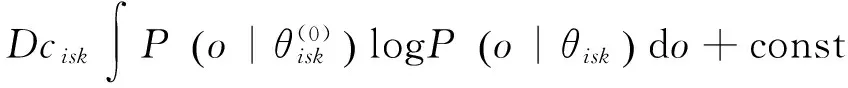
(22)


(23)

方差更新公式如式(25)所示,有兴趣的读者可参阅文献[19-20]。
4.4 针对发音质量评测的词图定制及高斯后验概率的计算
针对式(1)的帧规整后验概率定制的针对发音质量评测的词图,如图1所示,其中分子为参考文本的切分结果,分母为概率空间决定的解码网络。可见基于参考文本的后验概率可视为概率空间只含音素θj(其中j=id(r,n))时的基于概率空间的后验概率。
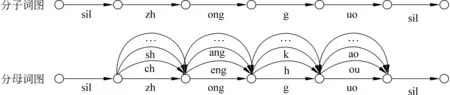
图1 针对发音质量的评测词图定制(以“中国”为例)
1) 支路帧规整后验概率的计算
从图2可知,所有支路起止帧均一致,因此支路后验概率可简化为类似于音素帧规整后验概率的形式。对于序号为j的音素,支路后验概率γj(ornt)的计算如式(26)所示。
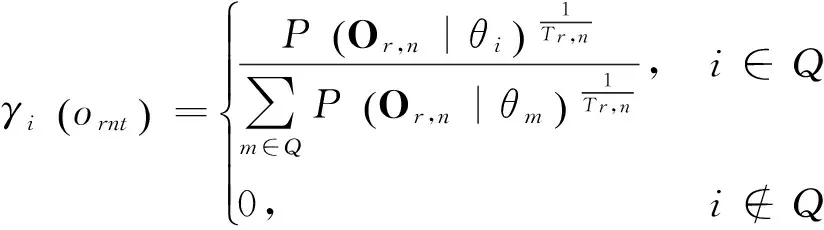
(26)
可见,支路帧规整后验概率的计算与评测的帧规整后验概率策略紧密相联。在计算得到支路帧规整后验概率后,状态及高斯级的后验概率与语音识别一致,下面加以简要介绍。

图2 状态级分母词图(以“zh”为例,图中状态指有效状态)注: 对于音素zh,在t时刻时,状态zh[2]的后验概率为1,其他状态(如zh[1]及zh[3])的后验概率为0。
2) 状态后验概率的计算
本文利用维比算法(可推广至前后项算法)进行状态后验概率的估计,如图2所示。首先将分子和分母词图切分至状态,再计算每帧的状态后验概率。
因此,对于给定支路i,状态后验概率可由式(28)得出
对特征Or,n进行解码后,若支路i的第t帧的为状态s则st(i,s,Or,n)=1,否则为0。
3) 高斯后验概率的计算
在得到支路帧规整后验概率及状态后验概率后,高斯后验概率如式(29)、(30)所示:
4.5 针对发音质量评测声学模型优化流程及在计算机辅助学习系统中的应用
针对发音质量评测的声学模型优化流程如图3所示,其包含声学模型的更新的回归系数的重训。
另外,通过本文优化算法得到的评测声学模型不能用于语音识别。因此测试时需利用“语音识别声学模型”(本文采用利用标准发音训练得到的初始声学模型进行语音识别)得到音素边界,再利用针对评测优化的声学模型(记为“评测声学模型”)计算帧规整后验概率,如图4所示。同时注意到评测声学模型利用式(24)(25)调整均值和方差得到,因此与初始声学模型拓扑完全结构一致,因此系统的时间复杂度不会增加,但空间复杂度会有所增加。

图3 针对发音质量的评测声学模型优化流程图

图4 评测声学模型在计算机辅助学习系统中的应用
5 数据库介绍及系统评价指标
5.1 普通话水平考试介绍及实验配置
普通话水平测试分为四个部分: 单字朗读(100个字,共计10分),双字词朗读(50个词,共计20分),篇章朗读(400字短文,共计30分)和自由说话(限时3分钟,共计40分),本文只考察前三个部分的自动评测。
5.2 数据库介绍
1) 标准发音数据集: 该集合包含30余名具有普通话水平测试一甲水平(相当于专业播音员)的录音数据,共计100小时[1]。
2) 普通话水平考试现场数据集: 共包含3 685份来自全国十余省的普通话水平考试现场录制的数据,考生发音水平参差不齐,每份数据有1~3名专业评分员的评分。本文将上述数据分为完全不交叠的训练集(3 187份,参与针对评测的声学模型优化)和测试集(498份)。
5.3 实验配置
本文实验采用39维的MFCC_0_D_A_Z声学特征,利用HTK工具对音素建立单音子(Mono-phone)隐马尔可夫模型(HMM)。包括静音模型(sil)、填充模型(filler)和短停模型(sp)在内一共67个HMM,其中声母(包括零声母)为3状态,韵母5状态。
实验采用机器分与人工分的相关度及均方根误差作为系统性能的评价指标,它们均反映了人机评分的一致程度。由于声学模型的优化不影响时长语速等评分特征的计算,因此后续实验只考察帧规整后验概率的性能。
6 实验及结论
6.1 以语音识别的声学模型作为初始模型的针对评测的声学模型优化实验
最大似然估计(MLE)建模型方式简单、 计算高效,且不需要精细的时间标注,少量错误对模型性能影响微乎其微,因此在计算机辅助学习系统中得到了广泛的应用。区分性训练是近十年来推动语音识别飞速发展的重要思想,其中以D. Povey在2002年提出的最小化音素错误(minimum phone error, MPE)具有代表性,同时本文方法也是受MPE的思想启发得到,因此实验将对比本文方法及语音识别的MPE算法。在作者之前的工作中[14],采用引入现场数据集进行声学模型训练会显著降低系统的评分性能,因此本文实验中的初始声学模型均根据标准发音数据集训练得到。
表1为分别采用MLE及MPE两种声学模型(由标准发音数据训练得到)作为初始模型时的实验结果;符号OPT为利用普通话水平考试现场数据,对初始模型进行的针对评测的声学模型优化,表中括号外的数字为相关度,括号内为均方根误差。
可见,无论对于何种声学模型,采用针对评测的声学模型优化均能显著地提升声学模型的评分性能。图5为在MPE+DEM配置下,训练集和测试集的收敛曲线,其中纵坐标为均方根误差。图中,“1A”代表第一次叠代时,仅更新声学模型的性能;“1L”代表第一次更新声学模型后,采用线性回归更新回归模型的性能,以此类推。
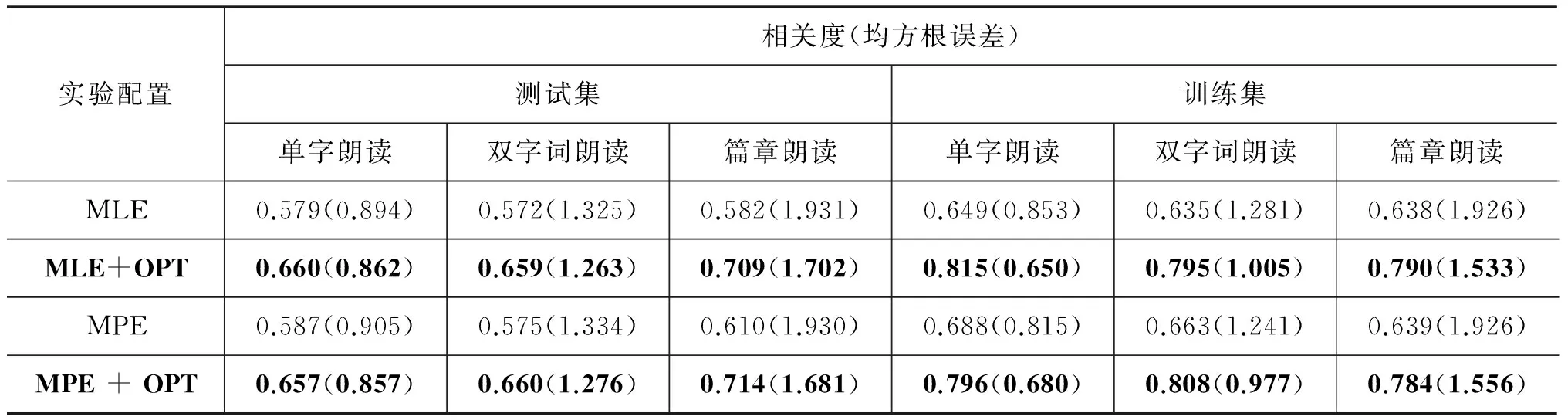
表1 以MLE和MPE声学模型作为初始模型的针对评测的声学模型优化的性能
可见训练集的均方误差随着叠代的进行而逐渐降低,证明了该方法有效性。在测试集上的性能略有波动,但总体上仍然朝着目标的方向前进。
6.2 在优化概率空间下的针对评测的声学模型优化
基于优化概率空间的声学模型优化的实现仅需要式(6)取代式(1)即可。实验以MPE为初始模型(由标准发音数据训练得到),实验结果如表2所示。
实验表明,无论在何种概率空间下,本文所提出的方法均能使声学模型的评分性能有着显著的提升;并且优化概率空间能进一步提升评测模型的性能。另外,值得注意的是在两类优化的概率空间下,由于概率空间音素个数远小于全音素概率空间,因此声学模型的训练速度及收敛速度均会明显提升。
6.3 基于音素相关的后验概率变换的针对评测的声学模型的优化
本文作者提出的音素评分模型[17]可视为音素相关后验概率变换(Phoneme-dependent posterior probability transformation,PPPT),其进一步弥补了帧规整后验概率与人主观评分的差异。将式(7)代入式(13),并经类似推导后,可得其统计量计算如式(31)所示。
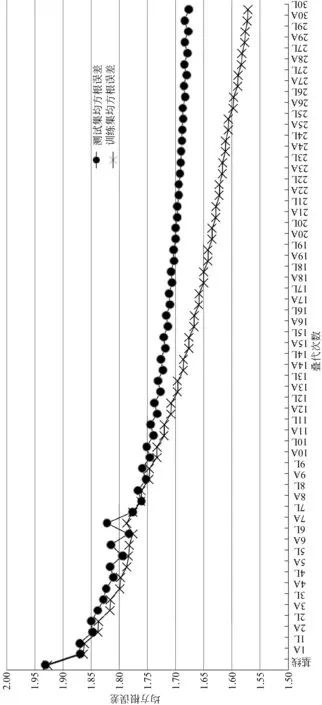

概率空间配置单字朗读双字词朗读篇章朗读全音素概率空间MPE(基线)0.587(0.918)0.575(1.355)0.610(1.930)MPE+OPT0.654(0.861)0.670(1.230)0.714(1.681)KLD聚类的概率空间MPE(基线)0.652(0.856)0.682(1.205)0.667(1.795)MPE+OPT0.719(0.784)0.754(1.061)0.749(1.601)基于典型错误优化的概率空间MPE(基线)0.701(0.801)0.705(1.168)0.700(1.832)MPE+OPT0.747(0.748)0.767(1.052)0.720(1.638)
注: 表中括号外为相关度,括号内为均方根误差

(31)
实验结果如表3所示。
实验表明,采用本文提出的针对评测的声学模型优化算法在各种配置下均有着显著收益。同时,由于PPPT的优化目标也是机器分与人工分的均方误差,因此系统性能提升幅度会有所下降。
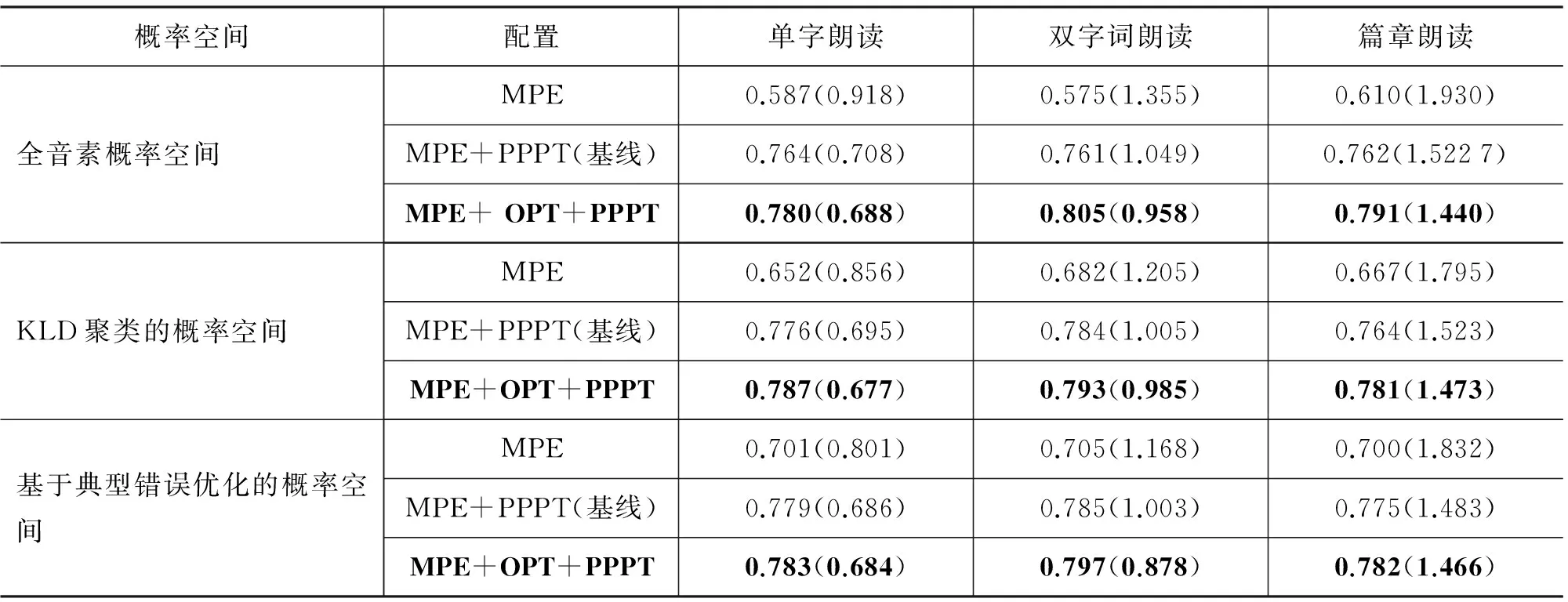
表3 基于音素相关后验概率变换的评测的声学模型优化的实验结果
注: 表中括号外为相关度,括号内为均方根误差
7 总结和展望
本文根据区分性训练思想,结合发音质量评测目标,提出了针对发音质量评测的声学模型的优化算法。算法以优化机器分与人工分均方根误差为目标,同时利用标准发音和非标准发音数据对声学模型进行优化,从根本上解决了采用传统的基于ASR的声学建模方式难以避免的训练与测试不匹配问题。实验在传统后验概率和各种优化配置上进行,系统性能均有显著的提升。
在发音质量评测领域,说话人自适应是一种能显著提升系统性能的手段[1,10]。然而,通常采用的MLE准则难以与最小化均方误差准则相容。因此,如何得到说话人相关的评测声学模型是下一步的工作重点。另外,基于ASR框架的声学具有明确的物理意义,即声学模型代表着标准发音模版,然而本文算法得到的声学模型不具备明确的物理意义,限制了进一步优化。因此,结合发音空间建模策略,建立有明确物理意义的评测声学模型是重要的工作方向。
[1] R H Wang, Q F Liu, S Wei. Putonghua proficiency test and evaluation[J]. Advances in Chinese Spoken Language Processing. Springer Press, 2006, 407-429.
[2] H L Franco, L Neumeyer, Y Kim, et al. Automatic pronunciation scoring for language instruction[C]//Proceedings of ICASSP 1997, 1465-1468.
[3] L Neumeyer, H Franco, V Digalakis, et al. Automatic scoring of pronunciation quality[J]. Speech Communication, 2000, 30(2-3): 83-93.
[4] S M Witt, S J Young. Phone-level pronunciation scoring and assessment for interactive language learning[J]. Speech Communication 2000, 30(2-3): 95-108.
[5] S M Witt. Use of speech recognition in computer assisted language learning. A dissertation of doctor’s degree for Cambridge, 1999.
[6] T Cincarek, R Gruhn, C Hacker, et al. Automatic pronunciation scoring words and sentences independent from the non-native’s first language[J]. Computer Speech and Language, 2009, 23(1): 65-88.
[7] S Wei, G P Hu, Y Hu, et al. A new method for mispronunciation detection using Support Vector Machine based on Pronunciation Space Models[J]. Speech Communication, 2009, 55(10): 896-905.
[8] 张峰. 基于统计模式识别发音错误自动检测的研究[D].中国科学技术大学博士毕业论文,2009年。
[9] C Cucchiarini, F D Wet, H Strik, et al. Automatic evaluation of Dutch pronunciation by using speech recognition technology[J]. ICSLP, 1998, 5: 1739-1742.
[10] 刘庆升.计算机辅助普通话发音评测关键技术研究[D].中国科学技术大学博士毕业论文,2009年。
[11] F. P. Ge, F. P. Pan, C. L. Liu, et al, An SVM-based mandarin pronunciation quality assessment system[J]. Advances in Intelligent and Soft Computing, 2009, 56: 255-265.
[12] 龚澍, 基于TANDEM的区分性训练在语音评测中的应用研究[D].中国科学技术大学硕士毕业论文,2010年。
[13] D. Povey, P. Woodland. Minimum phone error and I-smoothing for improved discriminative training[C]//Proceedings of ICASSP 2002: 105-108.
[14] K Yan, S Gong. Pronunciation proficiency evaluation based on discriminatively refined acoustic Models[J]. International Journal of Information Technology and Computer Science, 2011, 3(2): 17-23.
[15] 魏思,胡郁,王仁华. 普通话水平测试电子化系统[J].中文信息学报,2006,20(6): 89-96.
[16] 刘庆升,魏思,胡郁,等. 基于语言学知识的发音质量评价算法改进[J].中文信息学报,2007,21(4):92-96.
[17] 严可, 戴礼荣. 基于音素评分模型的发音标准度评测研究[J].中文信息学报,2011,25(5):101-108.
[18] L R Bahl, P F Brown, P V Souza, et al. Maximum mutual information estimation of hidden Markov model parameters for speech recognition[C]//Proceedings of ICASSP, 1986: 49-52.
[19] A P Dempster, N M Laird, D B Rubin. Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of the Royal Statistical Society, Series B (Methodological), 1997, 39(1): 1-38.
[20] R Schluter. Investigations on discriminative training criteria[D]. A dissertation for doctor’s degree, RWTH Aachen University, 2000.
[21] Y Normandin. Maximum mutual information estimation, and the speech recognition problem[D].A dissertation for doctor’s degree at McGill University, 1991.
[22] P Gopalakrishnan, D Kanevsky, A Nadas, et al. An inequality for rational functions with applications to some statistical estimation problems[J]. IEEE Transactions on Information Theory, 1991, 37(1): 107-113.
