数值模拟微小三通管支管倾角对环状流相分配的影响

周云龙，杨美，米列东

(东北电力大学，能源与动力工程学院，吉林吉林132012)

在微化工领域内，紧凑型和微小型热交换器的需求日益增加，如燃料电池周围需要配置大量水力半径在微米级的热交换器。三通管是一种常用的流体分配器，不可避免会出现相分配不均的情况[1-4]，工程上总是希望工质可以均匀分配给下游，以免影响下游设备的正常运行。

近些年来针对气液两相流过T形管时的相分布已进行了较深入的研究，Azzopardi等[5]和Yang[6]实验考察了各种相分离的影响因素。Stacey等[7]开始用数值模拟方法来模拟部分实验结果，但这些都是针对5 mm以上常规尺寸通道的研究。也有少量关于微小通道相分配的研究，Kim等[8]通过可视化实验发现微通道由于管壁狭小，气体很难携带液滴，液体只会以液膜的形式流动。何奎等[9]用可视化实验的方法研究了微小三通管道的相分配特性受上游流型的影响，弹状流相分配曲线主要位于气相富集区，环状流相分配曲线主要位于液相富集区。因此，要研究相分离特性，首先需要模拟特定流型下的管内流动。

环状流在两相流中占有最大的比例，是工业上典型的流型之一。本研究主要对微小三通管内流型为环状流时，通过改变支管与主管夹角，对分叉处两相流的偏流现象进行数值模拟。提出了对微通道侧支管结构的改进方法，尽可能地减少相分配的不均匀性。

1 微小三通管物理模型

1.1 模型的创建

本研究以微小三通通道作为物理模型，如图1所示。通道截面积为矩形（100 μm×800 μm），气液两相进口段为1 cm，混合段为2 cm，主支管与侧支管为1 cm。气相和液相分别从管道的左右侧进入，在混合区相遇形成环状流，经混合通道从主管道和右支管流出微流动系统。三通管道中的氮气和0.01%十二烷基硫酸钠(SDS)溶液的物理性质如表1所示。模拟氮气和0.01%SDS溶液在微通道内的相分配，通过改变支管倾角，来分析研究不同倾角α下的三通管中相分配特性的变化。本方案中选取了5组主管与支管夹角α的对比研究，俯视图如图2所示。

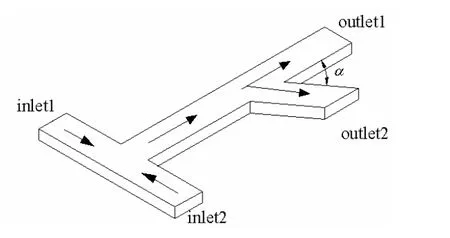
图1 微通小三通管道结构Fig.1 Schematic diagram of micro-junction

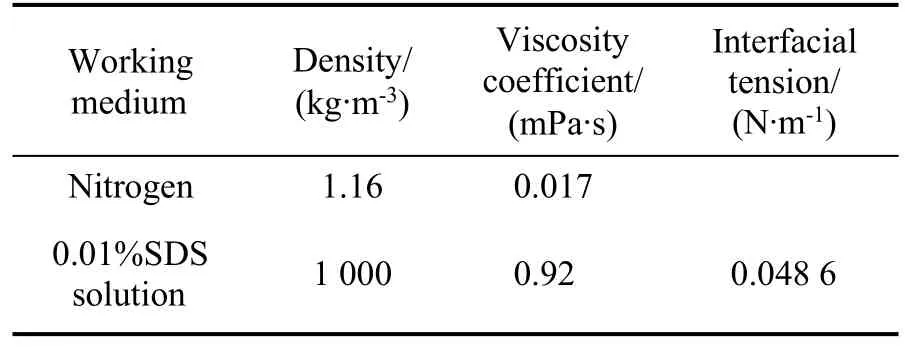
表1 氮气和0.01%SDS溶液的物理性质Table 1 Physical property of N2and 0.01%SDS liquid

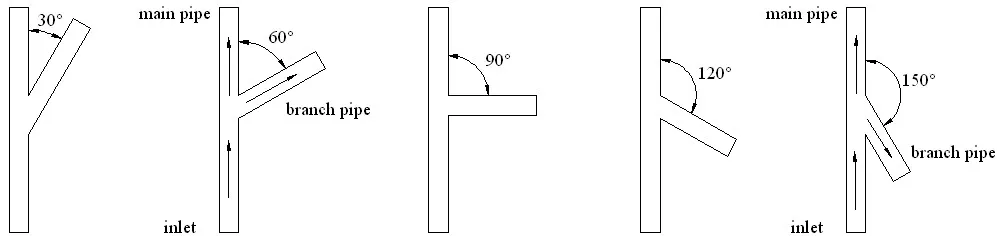
图2 不同支管倾角下微小三通道的平面Fig.2 Plane Fig.re of the different branch pipe dip angle in micro-junction

1.2 控制方程

使用流体体积模型（VOF）对气液两相界面进行追踪，通过Brackbill等提出的连续表面张力模型（CSF）将表面张力作为源项添加到动量方程中。模拟过程中使用的基本控制方程如下[11]

连续性方程

动量方程

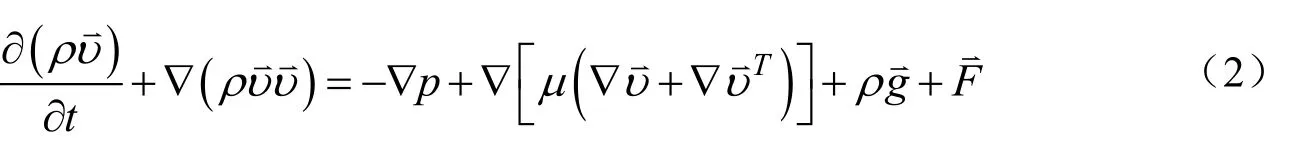
在该模型中，引入流体体积函数αi，用来表示每个控制体各相的体积分数

其中，密度和粘度为

在有限体积法中，将所计算的区域划分为一系列的控制体积，每个控制体积都由一个节点作为代表，对界面上的被求函数及其一阶导数做出假定，通过守恒型的控制方程对控制体积作积分来导出离散方程。用有限体积法导出的离散方程可以保证具有守恒特性，而且离散方程的系数具有明确的物理意义，是目前数值求解流动和传递问题最常用的一种方法。本研究求解流体力学方程，采用FLUENT 6.3版本，多相流模型中的流体体积模型。

1.3 边界条件和初始条件

使用5组不同的侧支管与主管道的角度α来模拟分析微小三通管道内气液两相偏流现象。连续相和分散相的入口均为速度入口(velocity inlet)控制，出口为自由出口(outflow)，给定入口边界上的速度，气体入口速度为0.5 m/s，液体的入口速度为0.05 m/s。出口处选择出流(outflow)边界条件，出口处压力设为105Pa。通道壁的设置为无滑移、无穿透的静止壁面。液体、气体和壁面三相交界处形成接触角为36°。

初始值的设定对最终的结果是否收敛有着重要影响，若初始值接近最后的收敛解，则能加快计算的速度，而如果远离收敛解，则会增加迭代步数，加长计算的过程，甚至造成计算无法收敛。本工作将对选定计算区域内的各个参数进行初始化。在计算非稳态前计算稳态得到一个合理的初始状态。

1.4 数值求解方法

微通道雷诺数小于200，按层流流动计算。微通道内压力降较小，气液两相视为不可压缩流体。Hazel[12]提出当Bo（重力与表面张力之比）远远大于1时，重力对系统有显著影响。本研究中由于特征尺寸小，表面张力凸显，微通道Bo小于1，所以模拟中不考虑重力影响，支管的放置方向和重力不会影响结果。气液两相流动过程中，两相界面随时间发生变化，因此整个过程属于非稳态过程。本研究中微通道中气液两相流的速度很低，因此模拟过程选择适用于低马赫数下流动的分离解法(Segregated Method)。另外，选用压力隐式算子分割算法（PISO）将压力－速度进行耦合，用压力插值算法（PRESTO）计算，用二阶迎风格式(second-order up-wind)。对动量方程进行离散，使用几何重构方案(Geo-Reconstruct)处理界面附近的插值。每次模拟过程中，时间步长和松弛因子需要适当地进行调整以保证收敛。

在直径19 mm的固定床反应器恒温段装填催化剂50 mL后通入氢气，氢气流量保持500 mL/min，并保持氢气压力2.8 MPa，升温到400℃并保持4 h即完成还原活化，然后降温至所需温度投料。

催化剂还原活化完毕后按照反应条件通入重整重芳烃和氢气作为原料，液体反应产物收集后称重记录。产物采用HP4890气相色谱仪分析，面积归一法定量。HP-1毛细管色谱柱，柱长50 m，内径0.32 mm，液膜厚度0.53 μm。进样口和检测器温度均为250℃，载气为氮气，流速1.5 mL/min，分流比100:1，氢火焰检测器氢气/空气体积比为10:1。程序升温：60℃保持1 min，以10℃/min升温至220℃保持3 min。

2 模拟结果与分析

2.1 数值模拟的可行性和准确性

模拟采用结构化网格进行网格的划分，不同网格数下微小三通管道支管出口截面上的液相体积分数分布如图3所示。研究中发现逐渐细化网格，当网格数为44 558时，计算结果不再随网格数的增加而改变，说明此时的网格划分达到计算精度的要求，花费时间最少，因此采用四方形网格数为44 558的网格划分保证计算精度的最大控制体积。

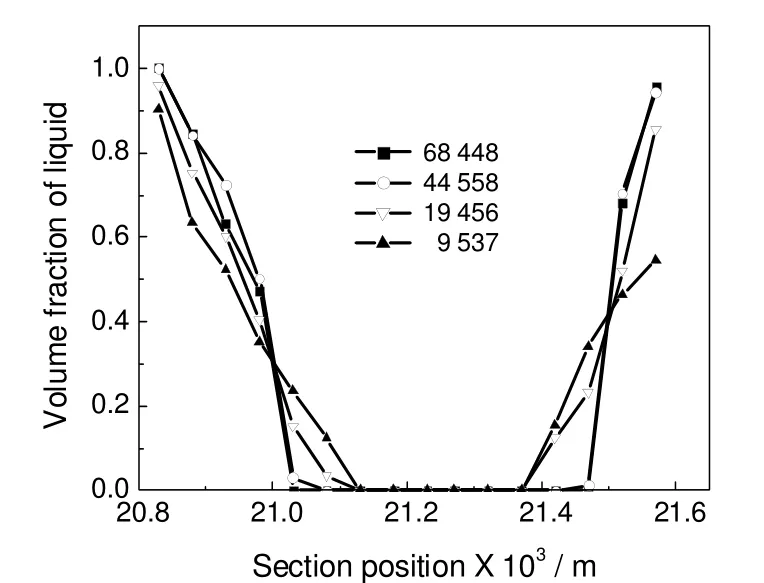
图3 不同网格数支管出口截面上液相体积分数分布Fig.3 Liquid phase volume fraction distribution of different grid number on exit section of branch

为了验证计算流体动力学(CFD)模拟结果的可行性和准确性，将本模型与周云龙[13]所做的T型微通道两相流流型及分离特性实验结果进行对比，采用与实验一致的空气和水。在常温常压下，水的表面张力为72 mN/m，粘度为0.92 mPa·s，密度为1 000 kg/m，空气粘度为0.001 8 mPa·s，密度为1.2 kg/m，折算液速为0.16 m/s，折算气速为4.0 m/s。模拟了在微小三通道中环状流的流型和相分配特性，与实验中CCD高速相机记录的液滴进行对比，结果如图4所示。由图4可知，CFD模拟了在微小三通道中环状流的流型和两相流的混合特性与实验结果有很好的一致性。

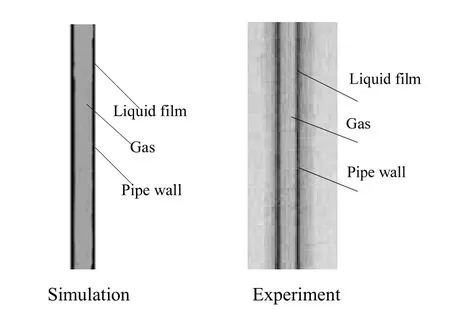
图4 环状流流型模拟与实验对比Fig.4 Annular flow pattern simulation and experiment comparison diagram

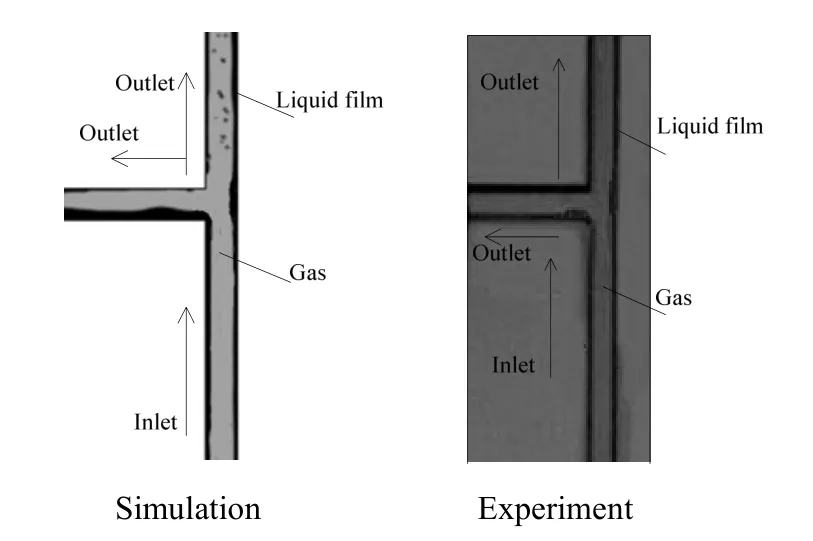
图5 微小三通管连接处环状流相分配环状流流型模拟与实验对比Fig.5 The phase split of annular flow at micro-junction simulation and experiment comparison diagram

设置5组不同的支管倾角（30°、60°、90°、120°、150°），对微小三通管内环状流相分配流动进行模拟。图5显示了支管倾角为90°的两相流体的相场分布。从模拟结果云图中可以看出，当两相流流经三通管连接处时，液相更容易流入支管，而大量气体都沿直流管流出。这与实验中[13]观察到的情况是一致的，证明了使用该模型可对微小三通道内的两相流进行准确和方便的CFD计算。

2.2 支管倾角对环状流相分配的影响

5组不同支管倾角的三通管内连接处的液相体积分数分布如图6所示。由6图可知，在相同边界条件下，环状流在一定范围内改变支管倾角对连接处的相分布有明显影响。气液两相环状流中，中间气流速度通常很大，而两侧液膜速度相对较小。气流区通过液膜交界面的拖拽作用使液膜上升速度高于液体入口速度。通过气液剪切机理，管道内壁面的剪切应力τω是环状流的主要流动阻力。在连接处，壁面附近的粘性力占主导地位，液体惯性力相对较小，近壁侧的液膜随着壁面粘性力和气体对液体的剪切应力进入支管，而中间气流速度较大，且不受壁面粘性力影响，其惯性力占主导地位，大部分进去主管道。支管倾角较小时，在延续环状流流场稳定性方面有较大优势，气体在侧支管的体积分数大于在主管中的体积分数。而支管倾角越大，在连接处动能损失越大，液体速度降低，环状流中液体受到中心处速度大的气体剪切作用越强，导致大量液体顺着管壁流入侧支管道。当倾角大于等于90°时，液体在侧支管的体积分数大于在主管中的体积分数，出现相分配不均现象。

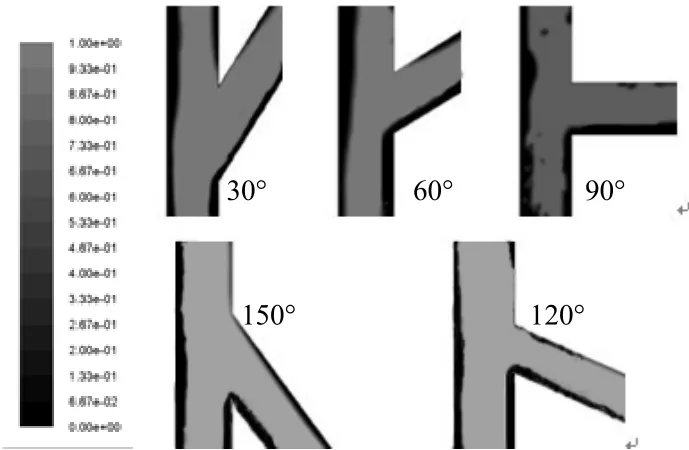
图6 不同倾角下连接处的气相体积分数分布Fig.6 Contours of volume fraction(N2)of the different branch pipe dip angle at junction

模拟计算不同支管角度下的支管出口气液两相质量流率。支管出口液相和气相采出分率计算公式如下

式中M3w，M1w分别代表支管出口液相质量流率和主管入口液相质量流率，kg/s；M3a，M1a分别代表支管出口气相质量流率和主管入口的气相质量流率，kg/s。流动为非稳态流动，在不同时刻支管采出率是不同的，取的是各个时间段的时均值。

图7中模拟数据点表示不同支管倾角对环状流相分配的影响。横坐标表示支管出口气相采出分率，纵坐标表示支管出口液相采出分率，对角线为两相均匀分配的等分线。在等分线的左上侧，表示液体优先从侧支管中采出，等分线的右下侧，表示气体优先从侧支管中采出。

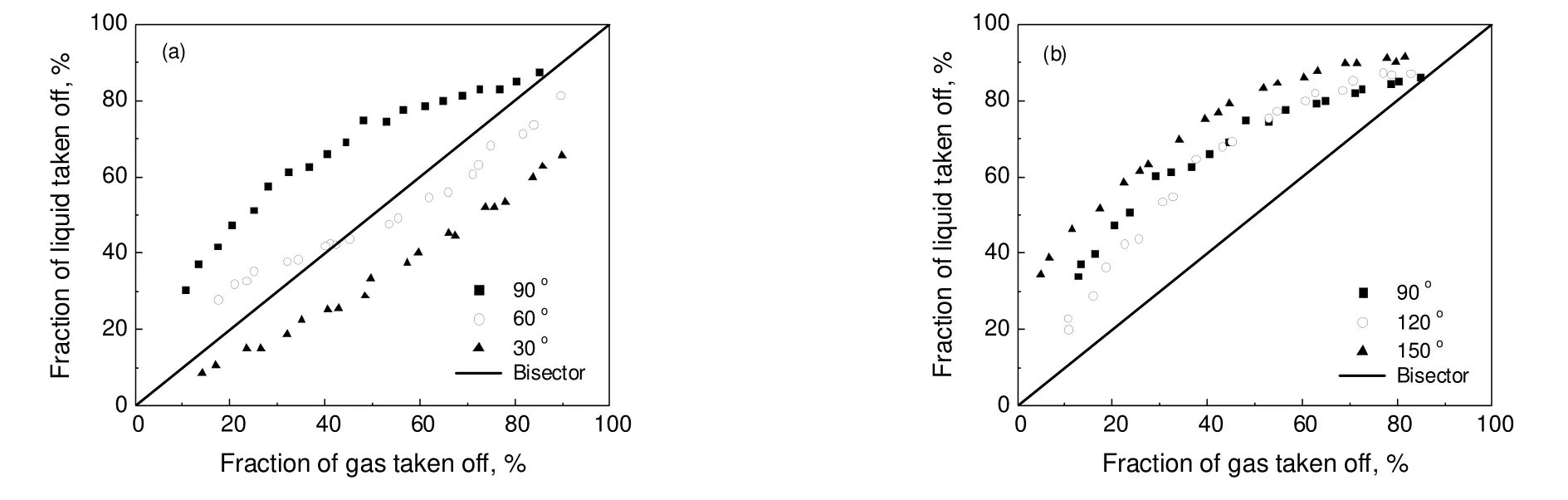
图7 不同支管倾角的相分配特性Fig.7 Phase split characteristics of the different branch pipe dip angle

由图7(a)可见，支管倾角为30°时，支管出口气相采出分率总大于支管出口液相采出分率。说明环状流在管内发生了不均匀分离，此时支管气相采出占优。支管倾角为60°时，在气相采出分率小于40%左右，在连接处均有较多的液相流入支管，在气相采出分率大于40%左右，在连接处均有较多的气相流入支管。

由图7(b)可见，当支管倾角为90°、120°、150°时，在连接处均有较多的液相流入支管，管内为环状流，且越靠近连接处液相体积分数越高。说明此时支管液相采出分率占优。在相同支管气相采出分率下，支管倾角为150°时，支管液相采出分率最高。当气相采出分率小于50%左右，倾角为90°的支管比倾角为120°的支管液相采出分率大。当气相采出分率大于50%左右，倾角为120°的支管比倾角为90°的支管液相采出分率大。

采用Yang[6]提出的分离效率表达方式，将分离效率定义为实际达到的两相分离与最大可能的两相分离之间的比值。

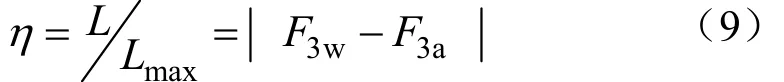
式中L表示实际达到的两相分离；Lmax最大可能的两相分离；F3w支管出口液相采出分率；F3a支管出口气相采出分率。由式（9）可以直接得到质量采出分率与分离效率的关系，结果如图8所示。由图8可见，环状流的相分配在支管倾角为60°，支管采出分率为40%左右时，质量分离效率最低，可获得最佳的相均匀分配。

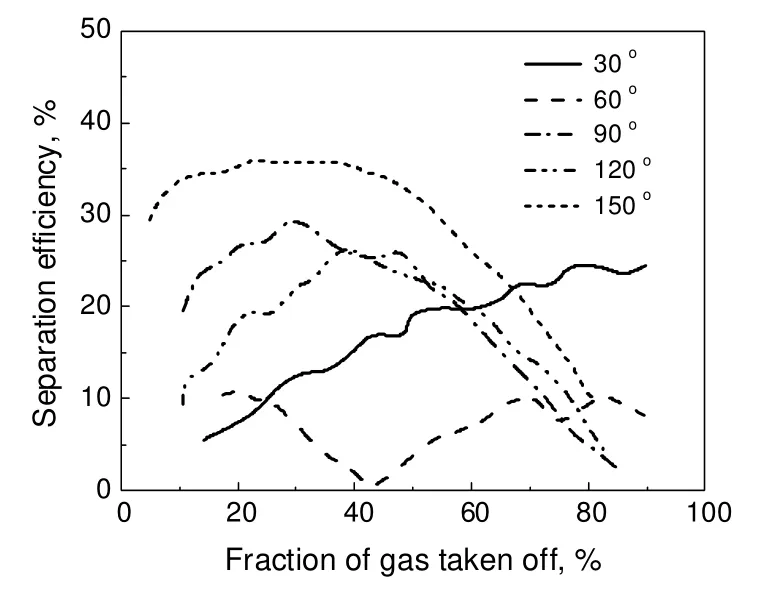
图8 新的相分离表示方式-不同倾角对相分配的影响Fig.8 New criterion-effect of the different branch pipe dip angle on phase split

2.3 支管倾角对环状流速度分布的影响

模拟得到的不同支管倾角下连接处速度分布如图9所示。气液两相环状流中，中间气流速度通常很大，而两侧液膜速度相对较小。在近壁面区域，液膜的粘性作用降低了液体的速度。支管倾角为60°的管内流动，经过三通管道，延续环状流稳定方面有较大优势，可基本保持主管内的环状流流型状态，且速度变化不大，经过连接处侧支管与主管速度分布一致，呈现中间速度大,越贴近管壁速度越小。而支管倾角为90°时，连接处有较大范围的速度变化，造成动能损失，密度大的液体比氮气会损失更多的动能，侧支管液相流体速度较低，更多液体进入支管中，造成相分配不均匀。当支管倾角为120°时，在连接处动能损失更大，液体的速度降低，受到速度大的气体的剪切力大，导致大量液体顺着管壁流入侧支管道，造成相分配不均。

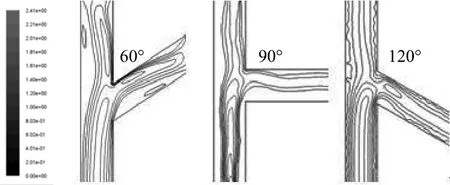
图9 不同支管倾角下连接处速度分布Fig.9 The velocity profile of the different branch pipe dip angle at junction

3 结论

通过对微小三通管道模型的数值模拟，得到入口流型为环状流时，不同支管倾角下的微小三通管道的相分配特性。当支管倾角为90°、120°、150°时，液相优先从侧支管中采出；支管倾角为30°时，气相优先从侧支管中采出；支管倾角为60°的管内流动，经过三通管道，延续环状流稳定方面有较大优势，可获得最佳的相均匀分配。而支管倾角越大，在连接处动能损失越大，液体速度降低，环状流中液体受到中心处速度大的气体剪切作用越强，导致大量液体顺着管壁流入侧支管道。倾角越大，流入侧支管的液体体积分数越大，造成相分配不均越明显。

微小三通管内的流量分配及相分配特性对微型工程设备的正常运行至关重要，为了减少微小三通管内的流量分配的不均匀性，应该采用主管与支管夹角为60°的微小三通管道。

[1] Hassel V,Stange T,Lowe H.Micro chemical processing at IMM-from pioneering work to customer-specific services[J].Lab on A Chip,2002,2(1):14N-21N.

[2] Ma Y G,Ji X Y,Wang D J,et.al.Measurement and correlation of pressure drop for gas-liquid two-phase flow in rectangular microchannels[J].Chinese Journal of Chemical Engineering,2010,18(6):940-947.

[3] Alamu M B,Azzopardi B J.Wave and drop periodicity in transient annular flow[J].Nuclear Engineering and Design,2011,241(12):5079-5092.

[4] Wren E,Azzopardi B J.Affecting the phase split at a large diameter T-junction by using baffles[J].Experimental Thermal and Fluid Science,2004,28(8):835-841.

[5] Azzopardi B J,Colman D A,Nicholson D.Plant application of a T-junction as a partial phase separator[J].Chemical Engineering Research and Design,2002,80(1):87-96.

[6] Yang L M.Liquid-liquid two-phase flows at T-junction and through expansion[D].Nottingham:The University of Nottingham,2003.

[7] Stacey T,Azzopardi B J,Conte G.The split of annular two-phase flow at a small diameter T-junction[J].International Journal of Multiphase Flow,2000,26(5):845-856.

[8] Kim S M,Mudawar I.Theoretical model for annular flow condensation in rectangular micro-channels[J].International Journal of Heat and Mass Transfer,2012,55(4):958-970.

[9] 何奎,汪双凤,黄间珍.气液两相流在微小T型三通中的相分配特性[J].化工学报,2011,62(S1):92-96.He Kui,Wang Shuangfeng,Huang Jianzhen.Phase split characteristic of two-phase flow through a micro-T-junction[J].CIESC Journal,2011,62(S1):92-96.

[10] 王琳琳,李国君,田辉,等.T型微通道内气液两相流数值模拟[J].西安交通大学学报,2011,45(9):65-69.Wang Linlin,Li Guojun,Tian Hui,et al.Numerical smulation of gas-liquid two-phase flow in a T-junction micro-channel[J].Journal of Xi’an Jiao Tong University,2011,45(9):65-69.

[11] Anderson J D.Computational fluid dynamics:the basics with applications[M].New York:McGraw Hill,1995:56-102.

[12] Hazel A L,Heil M.The steady propagation of a semi-infinite bubble into a tube of elliptical or rectangular cross-section[J].Journal of Fluid Mechanics,2002,470:91-114.

[13] 周云龙,刘博,刘袖,等.T型微通道内两相流流型及相分离特性[J].化学反应工程与工艺,2012,28(4):300-305.Zhou Yunlong,Liu Bo,Liu Xiu,et al.The flow pattern and phase splitting of two-phase flow in a micro-T-junction[J].Chemical Reaction Engineering and Technology,2012,28(4):300-305.