多段分级转化流化床颗粒浓度的数值模拟

王海艳，郝振华，王志雨，房倚天

(1.中国科学院山西煤炭化学研究所，煤转化国家重点实验室，山西太原030001;2.中国科学院大学，北京100049)

多段分级转化流化床气化炉(MFB)是一种新型流化床煤气化技术，由鼓泡射流流化床与快速流化床通过变径渐缩段耦合而成。MFB下部处于鼓泡流态化区，大颗粒煤粉颗粒在此进行气化反应，在中心射流区团聚成球，并通过选择性灰分离装置实现干法排灰过程[1]。为提高带出半焦细粉转化率，将原有扩大段改为快速流化床，使颗粒处于快速流态化区以便改变气固接触状况，通过提高循环比增加固体浓度和细粉停留时间，并提高快速床反应温度，进而提高半焦细粉碳转化率。此外上部快速床还可部分进煤，利用鼓泡流态化区高温煤气显热，进行煤的热解。如果热解、气化在同一流化床中进行，产生的挥发组分、轻烃类气体以及氢气会对半焦的气化产生抑制[2,3]。而MFB将煤的气化和热解过程分开进行，实现煤的分级转化，从而提高了碳的转化率。因此，MFB实际上为鼓泡流动和快速流动形态共存的可以实现煤的分级转化的一种新型粉煤气化技术。

多种流态形式的耦合技术已有研究，梁万才等[4]研究了灰熔聚流化床和气流床技术耦合的两段式煤气化炉，发现炉内流动形态较复杂，一、二段反应区连接的喉口使炉内形成返混区和局部回流区域。王德武等[5]将快速床与气固环流床耦合，发现快速床出口存在一个颗粒约束返混区。Gan等[6]研究了底部变径的新型快速床，发现床内同时存在多种流型，底部扩径段为浓度径向分布较均匀的密相床，上部为稀相床，下部流型对上部影响不大。

随着计算机技术以及颗粒动理学模型[7]、气固曳力模型[8,9]等的不断发展，计算流体动力学（CFD）成为考察流化床内气固两相流动行为的重要途径。张锴等[10]采用双流体模型模拟了Geldart B类物料的鼓泡流动特性，模拟结果与经典理论和实验结果相一致，表明该模型可以用来预测流化床内稠密气固两相流动的动力学特性。汤颜菲等[11]运用颗粒动理学理论与Gidaspow曳力模型模拟快速床内的稀疏气固流动，计算得到了较合理的颗粒轴向及径向浓度分布。本工作将在实验研究的基础上采用双流体模型对MFB内的气固流动特性进行模拟研究，主要分析在鼓泡和快速流动形态耦合作用下，MFB内整体以及局部浓度变化规律，为MFB的设计、操作以及优化提供理论指导。

图1 实验装置Fig.1 Schematic diagram of experimental appratus1-jetting fluidized bed;2-reducing pipe;3-riser;4-bag filter;5-secondary cyclone;6 primary cyclone;7-storage;8-standpipe;9-non-mechanicalvalve;10-butterfly valve;11-rootsblower;12-compressor

1 实验部分

实验在冷态多段分级转化流化床中完成的，装置如图1所示。装置主体由下部鼓泡射流流化床和上部快速床提升管组成。射流流化床内径300 mm，高1.5 m；快速床内径为150 mm，高8 m。它们之间通过缩径渐缩段连接。实验过程中，截面压降和局部固体浓度采用中国科学院过程工程研究所研制的压力传感器和PC6D型颗粒浓度测定仪测定，实验值取多次测量的平均值。

2 气固两相流动数学模型

欧拉双流体模型认为固相和流体相是共同存在且相互渗透的连续介质，两相流动用Navier-Stokes方程描述。李静海等[12]研究发现，曳力是颗粒与流体间相互作用的最基本形式，其他形式的相间作用在一定条件下可以忽略。为了封闭方程，固相压力和粘度采用颗粒动理学理论计算，气固相互作用则采用Gidaspow曳力模型实现。

气固两相质量守恒方程

气固两相动量守恒方程

其中

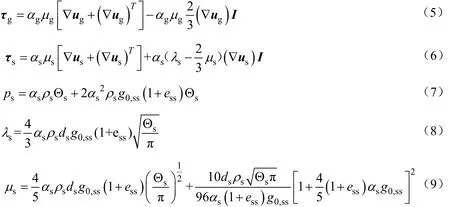
颗粒湍流动能守恒方程

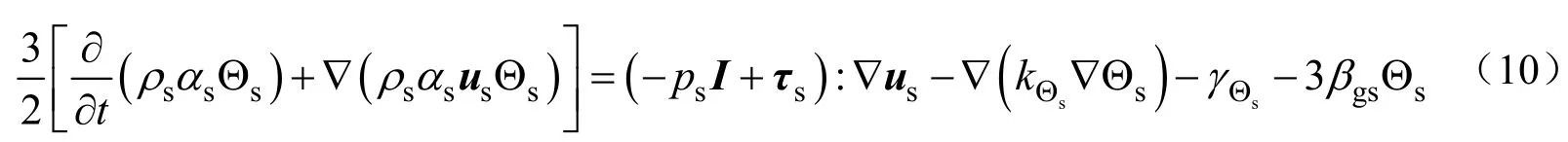
其中

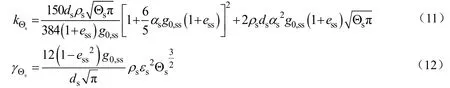
曳力模型

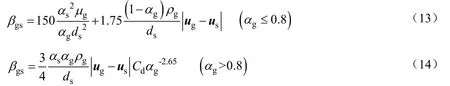
其中

3 结果与讨论

3.1 计算参数

取MFB床内0～5.0 m区域（图1虚线框部分），构建三维非结构网格进行计算。初始时刻鼓泡床内填充一定量的均匀球形固体颗粒，床内气相和固相初始速度均为零。入口按实验条件设置两相的速度及体积分数。顶部采用压力出口边界条件，在壁面处，气相采用无滑移边界条件，固相采用Sinclair和Jackson[13]提出的考虑颗粒与壁面的碰撞和颗粒与壁面的简单摩擦作用的壁面边界条件。空隙率采用QUICK离散格式，其它方程选择二阶迎风格式，采用Standard湍流模型，采用SIMPLE算法在多相流中的扩展版PC-SIMPLE算法。其它参数设置如表1所示。采用非稳态隐式求解，0.000 5 s的时间步长推进，直至计算收敛。为保持数据统计的稳定性，计算持续50 s，取后30 s为时间平均样本分析。

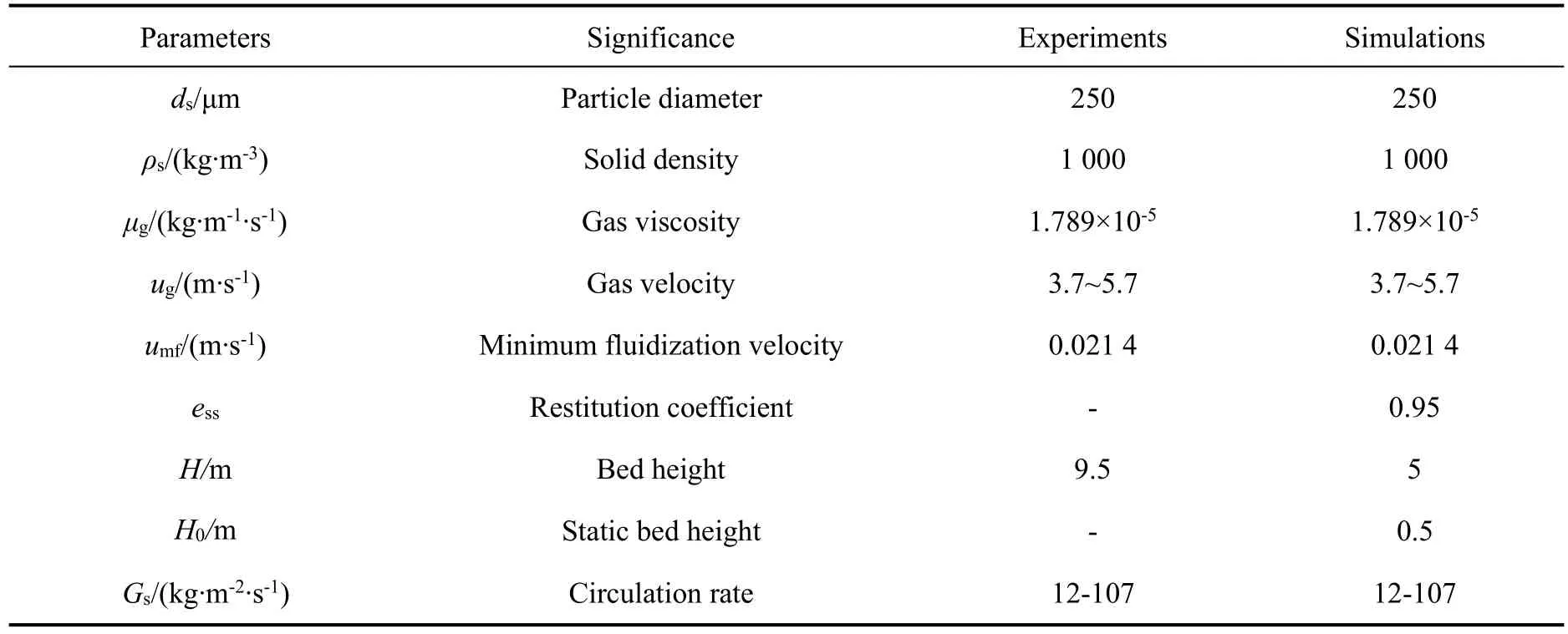
表1 实验和模拟参数Table 1 Parameters for experiments and simulations

3.2 MFB整体浓度分布

当ug为4.4 m/s、Gs为60 kg/(m2·s)时MFB内30 s到30.5 s时间内纵截面颗粒瞬时体积浓度云图如图2所示。由图可见，小气泡在锥形分布板上方形成，且沿床层上升过程中，发生聚并。MFB床下部平均浓度较高(αs＞0.20)，呈现明显的鼓泡流动形态。气体经变径渐缩段加速后，MFB床内上部颗粒浓度分布表现出强烈的不均匀性：边壁浓度高(αs＞0.12)、中心区域浓度低(αs＜0.04)，并形成了一个明显的气体通道。MFB床上部(H＞2.5 m)呈现明显的快速流动形态，这与实验中观察到的现象相符。

图2 颗粒瞬时浓度分布图（纵截面）Fig.2 Distribution of instantaneous concentrations of solid

当ug为4.4 m/s、Gs为60 kg/(m2·s)时，MFB内时均浓度轴向分布模拟与实验结果的对比如图3所示。右边的线表示MFB的结构示意图，H为2.5 m是回料口位置。由图可以看出，在回料口以上的MFB床内浓度呈指数型分布。回料口以下（H=1.9～2.5 m）部分其浓度自下而上逐渐增加，不同于传统的快速床浓度分布（见图右上角），从而使MFB床内鼓泡流动区域、变径渐缩段、快速床底部三部分轴向浓度总体上呈“C”型分布。由此可见，对于两种流型的耦合，其轴向浓度分布并非两种流态形式的简单叠加，变化过程较为复杂，在实际设计和操作当中应充分理解其内在规律。图中同时给出了实验测量结果，可以看出模拟结果与实验测量结果较为接近。

图3 时均颗粒浓度轴向分布Fig.3 Axial distribution of solid concentrations

3.3 MFB快速床稀相段颗粒浓度分布

ug为4.4 m/s、Gs为60 kg/(m2·s)时，快速床内的时均径向浓度分布的实验与模拟结果的比较如图4所示。由图可见快速床内径向浓度分布呈现中心稀(0.02＜αs＜0.04)、边壁浓(αs＞0.10)的环-核流动结构特征。在中心区域模拟结果与实验实测结果基本吻合，但在边壁区域有一定的差异，最大相对误差达到24%，这是因为在边壁区域颗粒浓度高，出现了颗粒团聚物，而基于平均化的Gidaspow曳力模型未充分考虑颗粒聚团的影响，致使边壁区域的模拟与实验数值差异增大。

图4 颗粒时均浓度径向分布Fig.4 Radial distribution of solid concentrations

模拟得到的操作条件对颗粒浓度的影响如图5和图6所示。由图可以看出，快速床呈现颗粒浓度呈现中心低（αs=0.02～0.04）、边壁浓（αs＞0.10）的不均匀分布。由图可以看出，在不同的径向范围内，由于中心区（r/R＜0.2）和边壁区(r/R＞0.8)的颗粒运动状态有所不同，颗粒浓度随Gs和（或）ug的变化幅度不同：中心区颗粒聚集不明显，气固流动发展充分，从而受Gs和（或）ug的影响较小。而边壁区，颗粒浓度较高，聚集倾向更明显，维持其运动状态耗能较多，因此受Gs和（或）ug的影响较大。

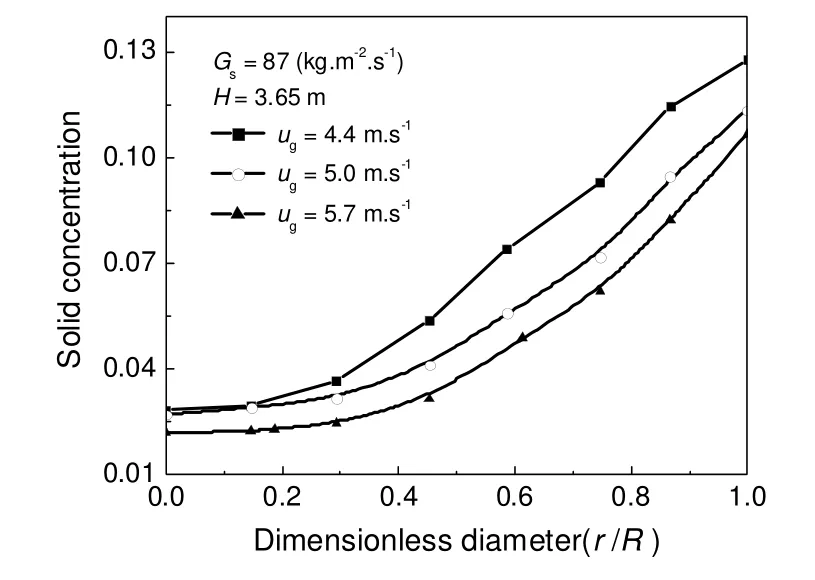
图5 循环速率对颗粒浓度的影响Fig.5 Solid concentrations as a function of circulation rates

图6 表观气速对颗粒浓度的影响Fig.6 Solid concentrations as a function of gas velocity

3.4 快速床下段回料口附近颗粒浓度分布

模拟得到的回料口附近截面颗粒运动及分布情况如图7所示。由速度矢量图可以看出，循环物料进入快速床后小部分颗粒被上升的气流夹带向上运动，大部分颗粒在斜向下的动量作用下冲向另一侧的边壁，形成偏流。由瞬时浓度分布图可见，颗粒浓度在中心处很低（αs＜0.05），边壁处较高，颗粒浓度分布不对称，进料口一侧的颗粒浓度明显低于另一侧。且颗粒浓度在入口处（H=2.5m）偏流现象最为严重，沿轴向向两端逐渐减弱。

图7 回料口附近截面颗粒浓度和速度分布Fig.7 Distribution of solid concentrations and solid velocity

ug为4.4 m/s，Gs为60 kg/(m2·s)操作条件下，回料口截面（H=2.5m）处的颗粒浓度随时间的波动结果如图8和图9所示。

图8 颗粒瞬时浓度随时间的变化Fig.8 Variations of instantaneous concentration of solid

由图8可以看出，不同的径向位置处（r/R：无因次半径）的颗粒浓度平均值随r/R的增大而增大，由中心至边壁区域，截面浓度平均值在0.046～0.086内变化。由图9可以看出，在同一截面上，不同位置的浓度波动相差较大，r/R为0.0～0.95时，标准偏差在0.025～0.075内逐渐增大，即r/R越大，浓度波动越大。标准偏差的径向分布和浓度的分布趋势是相一致的。浓度越大，气固相互作用越强烈，波动也越大，偏离平均值的程度也越大。

图9 标准偏差的径向分布Fig.9 Radial distribution of standard deviations

3.5 过渡渐缩段的颗粒浓度分布

过渡渐缩段将下部鼓泡射流床和上部快速床相连接，使床径由0.3 m减小为0.15 m，气体表观速度迅速增大，快速床下落的颗粒被高速的气体夹带上升，因而此区域颗粒浓度较低(αs＜0.01)。但是伴随着气泡在床面的崩破，会发生颗粒弹溅现象，弹溅现象的发生会对操作稳定性产生影响[15]，本实验过程中也观察到了这一现象的存在。

图10表示一个弹溅过程内过渡渐缩段内的颗粒浓度变化情况。由图可以看出，颗粒发生弹溅，会使过渡段内的颗粒浓度迅速增大(αs＞0.1)，弹溅过程结束后，此区域的浓度重新恢复到一个较低的状态。在煤粉气化过程中，射流床中颗粒温度较高，弹溅到边壁的颗粒如果浓度过高，可能会发生结渣，这对气化是很不利的，因此实际操作过程中应充分考虑颗粒弹溅带来的影响。

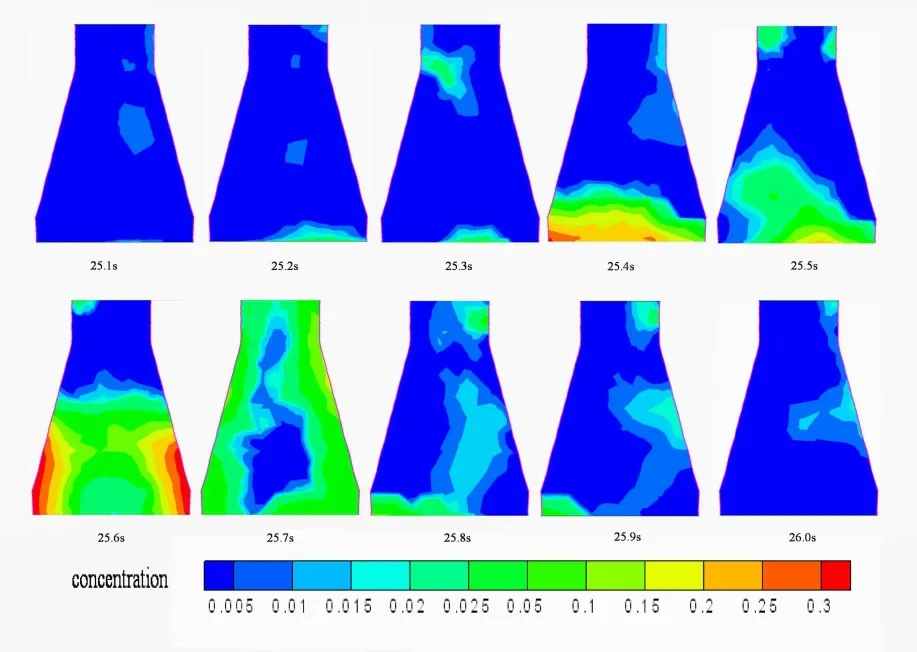
图10 颗粒瞬时浓度分布（过渡渐缩段）Fig.10 Distribution of instantaneous concentrations of solid

4 结论

a）采用双流体模型对MFB内气固两相流动特性进行数值模拟计算。模拟计算结果与实验结果较接近，结果显示回料口下段颗粒浓度呈“C”型分布，回料口上段颗粒浓度成指数型分布，表明两种流型的耦合，其轴向浓度分布并非两种流态形式的简单叠加，其变化过程较为复杂。

b）考察了快速床稀相段颗粒浓度的径向分布，结果表明，在中心区域，模拟结果与实验结果较为接近，边壁区误差较大，最大达到24%。径向各位置的颗粒浓度随ug的减小，Gs的增加而增加，边壁区增加幅度更为明显，对操作条件的变化敏感性更强。

c）考察了回料口附近颗粒浓度的分布情况，结果表明，固体物料通过回料口进入后，在快速床内形成偏流，回料口一侧的浓度显著低于另一侧，这种不对称分布沿轴向逐渐减弱。

d）考察了回料口(H=2.5 m)处颗粒浓度的波动情况。结果表明，同一截面上，不同位置的浓度波动相差也较大，r/R为0.0～0.95时，标准偏差在0.025～0.075内逐渐增大，即越靠近边壁，波动越剧烈。

e）考察了过渡渐缩段内的颗粒浓度的变化情况。结果表明，过渡渐缩段颗粒浓度较低(αs＜0.01)，但颗粒弹溅现象的出现会使颗粒浓度迅速增加(αs＞0.1)，实际操作中应充分考虑弹溅对气化过程的影响。

符号说明

[1] 髙鹍,吴晋沪,王洋.灰熔聚流化床气化炉分布分离结构的模拟研究[J].燃料化学学报,2006,34(4):487-491.Gao Kun,Wu Jinhu,Wang Yang.Simulation on gas and solid flow of ash-agglomerating fluidized bed gasifier with different structures of gas distributor and ash separator[J].Journal of Fuel Chemistry and Technology,2006,34(4):487-491.

[2] Lackermeier U,Werther J.Flow phenomena in the exit zone of a circulating fluidized bed[J].Chemical Engineering and Processing,2002,41(9):771-783.

[3] Bayasaikhan B,Sonoyama N,Hosokai S,et al.Inhibition of steam gasification of char by volatiles in a fl uidized bed under continuous feeding of a brown coal[J].Fuel,2006,85(3):340-349.

[4] 梁万才,赵建涛,吴晋沪,等.两段式气流床煤气化炉内气固流动数值模拟研究[J].燃料化学学报,2007,35(3):359-365.Liang Wancai,Zhao Jiantao,Wu Jinhu,et al.Numerical simulation of the gas-solid flow in the two-stage entrained flow coal gasifier[J].Journal of Fuel Chemistry and Technology,2007,35(3):359-365.

[5] 王德武,卢春喜.提升管-流化床耦合反应器颗粒约束返混区的流动特性及约束作用分析[J].化工学报,2008,59(4):859-865.Wang Dewu,Lu Chunxi.Particle flow behavior and restriction in back-mixing region of riser-fluidized bed coupled reactor[J].Journal of Chemical Industry and Engineering(China),2008,59(4):859-865.

[6] Gan J Q,Yang C H,Li C Y,et al.Gas-solid flow patterns in a novel multi-regime riser[J].Chemical Engineering Journal,2011,178:297-305.

[7] Gidaspow D.Multiphase flow and fluidization[M].Boston:Academic Press,1994.

[8] Yang N,Wang W,Ge W,et al.CFD simulation of concurrent-up gas-solid flow in circulating fluidized beds with structure-dependent drag coefficient[J].Chemical Engineering Journal,2003,96(1-3):71-80.

[9] 林亮成,郑忠,陈伟,等.不同曳力模型对鼓泡床内气固两相流的模拟研究[J].化学反应工程与工艺,2010,26(5):390-398.Lin Liangcheng,Zheng Zhong,Chen Wei,et al.A simulation study of gas-solid two phase flow in a bubbling fluidized bed with various drag force models[J].Chemical Reaction Engineering and Technology,2010,26(5):390-398.

[10] 张锴，Brandani Stefano.流化床内颗粒流体两相流的CFD模拟[J].化工学报,2010,61(9):2193-2206.Zhang Kai，Brandani Stefano.CFD simulation of particle-fluid two-phase flow in fluidized beds[J].Journal of Chemical Industry and Engineering(China),2010,61(9):2193-2206.

[11] 汤颜菲,王嘉骏,冯连芳,等.提升管内气固流动行为的数值模拟[J].化学反应工程与工艺,2006,22(5):445-450.Tang Yanfei,Wang Jiajun,Feng Lianfang,et al.CFD simulation of gas and solid flow behavior in a riser[J].Chemical Reaction Engineering and Technology,2006,22(5):445-450.

[12] 李静海,欧阳洁,高士秋,等.颗粒流体复杂系统的多尺度模拟[M].北京:科学出版社,2005:79-83.

[13] Sinclair J L,Jackson R.Gas-particle flow in a vertical pipe with particle-particle interaction[J].American Institute of Chemical Engineers,1989,35(9):1473-1486.

[14] 黄卫星,易彬,杨颖,等.循环床气固提升管中颗粒浓度的轴向分布[J].四川大学学报(工程科学版),2000,32(6):38-41.Huang Weixing,Yi Bin,Yang Ying,et al.Axial distributions of averaged solids holdups in a 16 m CFB riser[J].Journal of Sichuan University(Engineering Science Edition),2000,32(6):38-41.

[15] 许徐飞,周琦,邹涛,等.溢流管式多层气固流化床稳定操作气速范围的影响因素[J].过程工程学报,2012,12(3):361-368.Xu Xufei,Zhou Qi,Zou Tao,et al.Gas velocity range of stable operation in a gas-solid multi-stage fluidized bed with overflow standpipes[J].The Chinese Journal of Process Engineering,2012,12(3):361-368.