指数分布下无替换定数截尾寿命二次抽样检验

赵晨皓， 宋向东

(燕山大学理学院 河北秦皇岛066004)

0 引言

近年来，截尾寿命检验［1］得到了广泛的研究，这种检验要求进行到投试样品中有部分失效就停止检验．截尾寿命检验分为定数截尾寿命检验［2］和定时截尾寿命检验［3］．根据以往的经验，产品的寿命一般服从指数分布［4］和威布尔分布［5］，在这里，本文只讨论指数分布下的定数截尾寿命检验［6］，称

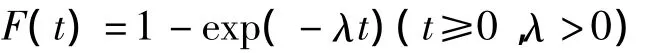
的寿命分布为指数分布，其中λ为常数．定数截尾寿命检验是指n个独立同型产品从t=0开始进行寿命检验，试验到第r个失效时刻终止，考虑无替换定数截尾情形，假设n个样品受试，试验到tr时停止，此时获得前r个寿命数据，r个失效时间记录为t1≤t2≤…≤tr(1＜r≤n)，则平均寿命θ的估计量为 θ^=Tr/r，式中

在定数截尾寿命检验一次抽样［7］中，记生产方风险质量水平为θ0，也称可接受平均寿命θ0，使用方风险质量水平为θ1，也称极限平均寿命θ1，生产方风险α，使用方风险β．验收规则为:当θ^≥c时，接受该批;当＜ c时，拒绝该批．将此方案记为方案(n，c，r)，其中 n 为样本量，c为接收常数，r为截尾数．方案(n，c，r)的接受概率为 Pa(θ)=Pa≥c)．

本方案与n无关，为了确定产品检验的样品量，规定样本量n与截尾数r按4∶1进行计算来制定方案，下面的定数截尾寿命二次抽样方案都按此比例进行．

1 定数截尾寿命二次抽样方案简介

2 接收概率

二次方案接收概率的一般表达式为

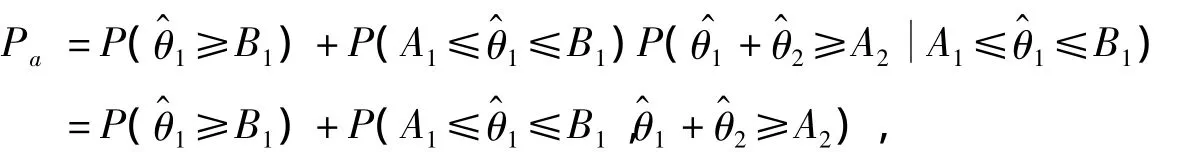
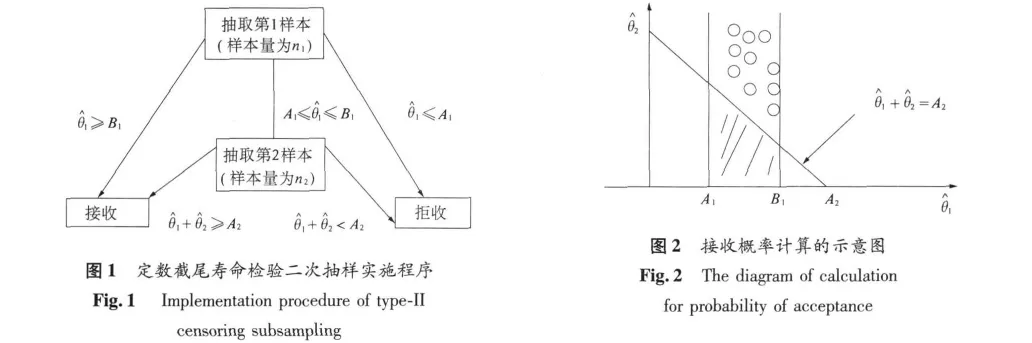
下面用图2表示出需要求的第2项这个概率．

在图2中，A1与B1所加的条形区域代表第1次抽样不能做出判断继续抽样的概率，即图2中有圈的区域代表第1样本不能做出接收与拒收的条件下，第2样本判批接收的概率，即

因为要求的是有圈的区域代表的概率，从图2中可以看出，可以用条形区域减去有斜线的区域的概率，所以接收概率可以写为

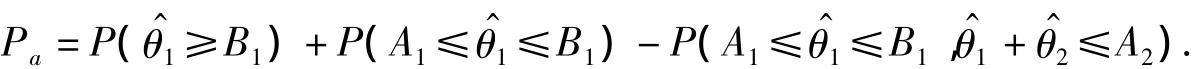
下面介绍一下求有斜线区域代表的概率的方法．

可以采用数值计算的方法，即将这部分分割，等分为n份近似的矩形区域，计算在每一个小矩形的概率，然后进行累积求和即可．

取其中一个小矩形，横坐标的两个端点值为X(i)和X(i+1)，中点值为，为了计算的精确，纵坐标的值为A2－Xd，那么在这个小矩形中的概率为

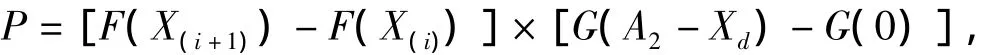
从而在整个区域的概率为

因此，二次抽样的接收概率为

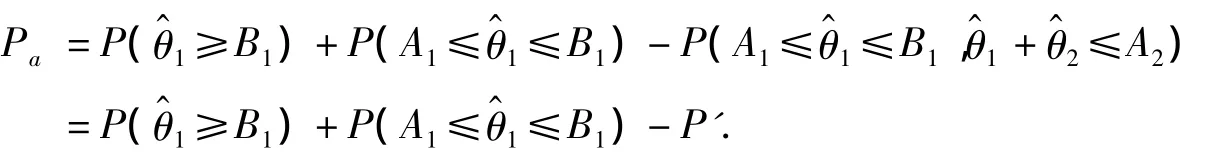
由于(2r θ^/θ)～χ2(2r)，为了使二次抽样方案和一次抽样方案能够对应，使用相同的分布进行计算．二次抽样一般习惯上抽取的n1，n2是相同的，即n1=n2，那么也就是规定截尾数r1=r2，以后统一使用r．因为θ^1与θ^2都是代表着平均寿命，所以它们服从同样的分布，有

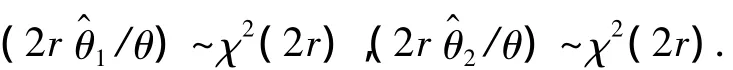
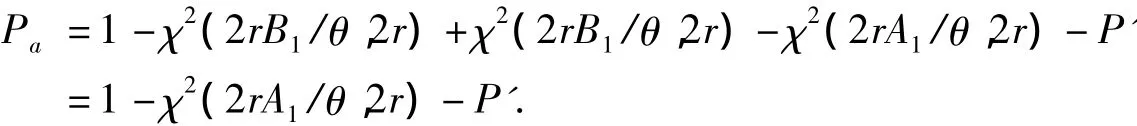
3 平均样本量ASN

二次抽样方案［8］的平均样本量是

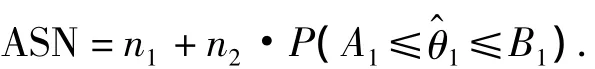
4 一次方案与二次方案的比较

制定的二次抽样方案从结果上看是与相应的一次方案等效的，也就是说具有相同的OC曲线，下面给出一个例题，制定一次抽样方案和一个相应的二次抽样方案，在拟合等效的情况下进行平均样本量的比较．

例 对某批产品进行定数截尾寿命试验．设定:θ0=900 h，θ1=300 h，α =0．05，β =0．10．

在给定的条件下，通过计算得到定数截尾寿命一次抽样方案是(32，8，448)，二次抽样方案是(24，6，350，480，1 000)，下面给出2个方案接收概率曲线的拟合图(见图3)．

在等效的情况下，比较一下平均样本量，见图4．

从图4上看出，在等效的抽样效果下，二次抽样的平均样本量小于一次抽样的样本量，由此可以知道二次抽样方案在节省样本量上是很好的．

5 结论

本文根据定数截尾寿命一次抽样方案，建立了定数截尾寿命二次抽样方案，给出了二次抽样方案的参数以及实施过程，给出在什么情况下做出如何判断的规则．同时，本文重点给出了二次抽样方案的接收概率，详细介绍了接收概率的理论计算过程．通过介绍定数截尾寿命二次抽样平均样本量的理论，将一次抽样与二次抽样的平均样本量进行比较，发现二次抽样方案相对于一次抽样方案确实节省样本容量．

［1］ 袁建国，秦士嘉，周尊英，等．抽样检验原理与应用［M］．北京:中国计量出版社，2002:187－196．

［2］ 张丕一．定数截尾寿命试验下指数分布平均寿命的置信限的优良性［J］．青岛大学学报:自然科学版，1999，12(4):14－19．

［3］ 吴启光，吕建华．定时截尾下指数分布产品可靠性抽样检验方案［J］．系统科学与数学，2003，23(2):145－154．

［4］ 茆诗松，王静龙，濮晓龙．高等数理统计［M］．北京:高等教育出版社，1998:35－56．

［5］ 吴启光，李国英，顾岚，等．双参数威布尔分布下可靠性抽样检验［J］．应用概率统计，2004，21(3):270－286．

［6］ 武东，汤银才．指数分布逐次定数截尾试验的多层贝叶斯估计［J］．上海第二工业大学学报，2011，28(2):113－116．

［7］ 孙艳君，宋立新．有替换定数截尾寿命试验中可靠性的经验Bayes估计［J］．长春师范学院学报:自然科学版，2010，29(1):1－3．

［8］ 周玲玲，余春花．计量调整型抽样检验系统的设计与实现［J］．统计与决策，2004，2(1):20－21．