NMF方法在遮挡人耳识别中的应用

王 瑜

(北京工商大学计算机与信息工程学院 北京100048)

0 引言

遮挡一直是人耳识别的典型难题，严重阻碍该生物特征识别技术的快速发展．在数据分析工作中，一个基本的原则是寻找恰当的数据表示，一方面要能够清晰的表达隐含的数据结构，另一方面要达到降维的目的，以便后期的计算研究工作．

NMF是近年来提出的一种新颖的数据表达方式，它以一种无监督的方式寻找目标的局部特征，因此与主元分析 PCA(principal component analysis)［1］、线性判决分析 LDA(linear discriminant analysis)［2］和独立元分析ICA(independent component analysis)［3］等线性子空间特征提取方法相比而言，更适合解决识别中的局部遮挡问题．

现存的基于局部特征的数据表达方式还有LFA(local feature analysis)［4］和ICA等方法，但是这些方法的线性叠加特征系数有可能是正的，也有可能是负的，因此在复杂的叠加过程中会有正负抵消现象发生，这就使得局部构成整体的思想缺乏直观性的理解．同这些方法相比，由NMF方法得到的基空间和重构特征系数被加以非负的限制条件，使得在重构输入数据的线性叠加过程中只有加而没有减，由局部累加为整体，因此NMF方法不仅从理论上，而且从直观上更容易被理解为基于局部的数据表示方法，这也是考虑将NMF方法应用于遮挡条件下人耳识别的主要原因．

1NMF

NMF方法是文［5］于1999年提出的，经过大量的实验证明，在多维变量数据分解中，NMF是一种行之有效的方法．NMF的主要思想是对输入图像V分解得到的基空间W和重构系数H加以非负性限制，保证矩阵W和H中的元素均为非负．

目前，NMF有两种不同的算法，经证明在实际应用中都非常有效，这两种方法只是在迭代规则上略有不同，一种以最小平方误差为衡量准则，简称为NMFSE，而另一种以最小K-L离散度为衡量准则，简称为NMFDIV．以最小平方误差为目标函数值的迭代规则为:

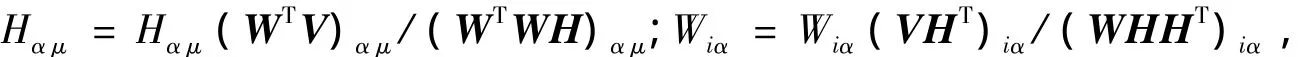
式中的下标均表示行列标记，前面的字母表示行，后面的字母表示列，下面迭代公式的下标意义均同．以最小K-L离散度为目标函数值的迭代规则为:

2 基于NMF的其他方法

NMF方法尽管在实际中已经得到认可和应用，但是并不能保证一定会得到理想的局部空间表示结果，而且识别率也比较低．因此，在NMF的基础上，又发展了其他的非负矩阵因子算法．

2．1LNMF

LNMF［6］是在原始NMF方法的启发下提出的，除了对基空间W和特征空间H的非负性限制外，还对低维特征空间hj增加了稀疏性的限制，并且基空间W也增加了特征定位．稀疏性的表示源自于稀疏编码(sparse coding)，稀疏编码是参照图解表示提出来的，在这种图解中只有几个表示单元有效地显示数据矢量，而其他大多数表示单元则接近零值，将稀疏编码这个含义引用到稀疏性的概念中，那么稀疏性可用公式定义为Sparseness其中，X为一个向量，xi是其元素，n为元素的个数，当且仅当X中只有一个非零元素时，向量的稀疏性最大，其值为1;当且仅当所有元素相等时，向量的稀疏性最小，其值为零．

在假设V=［Vij］=WH，U=［uij］=WTW，B=［bij］=HHT的条件下，LNMF增加了3个限制条件:最大化H的稀疏性;最大化W的表示信息;最大化W的正交性．为此，可以得到LNMF方法迭代规则为:

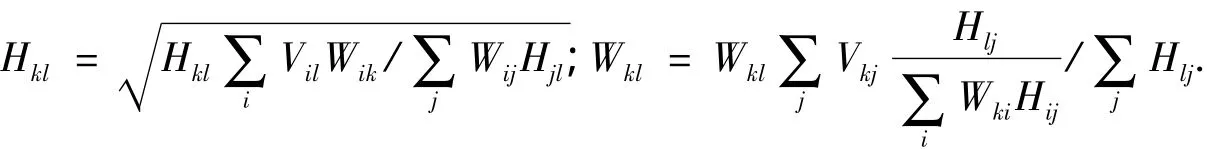
2．2NNSC

Hoyer［7］于2002年首次提出NNSC方法，并将其应用于人脸特征识别．此方法的目的就是通过选择适当的特征系数hj来寻找一组基空间wj，以便使得输入矢量vj仅用很少的非零特征系数hj来描述，进而达到减少重构误差和增加特征系数H的稀疏性的目的．NNSC的迭代公式为:

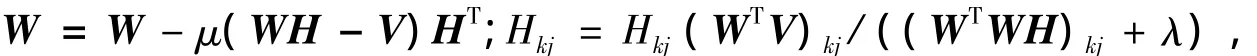
其中μ与λ均为参数，μ＞0为步长，λ决定稀疏程度．

2．3SNMF

NNSC使用投影梯度下降法，这对迭代步长的选择很敏感，而迭代步长只能通过经验来选取，因而并不能保证分解的基空间W为非负，而是在迭代中强制性的将小于零的元素设置为零，为此，这种投影梯度下降法只有在步长μ足够小的情况下才能保证目标函数收敛，但是无法保证不会出现局部最小值．与NNSC相比，SNMF的算法使用乘法迭代规则，因此可以保证分解的基空间W和特征空间H均为非负．SNMF的迭代规则为［8］:

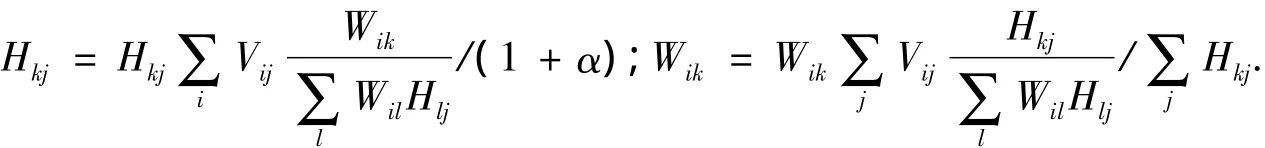
2．4NMFSC

为了得到较好的基空间W和特征空间H的稀疏性，NMFSC方法在NMF方法的基础上增加了稀疏性的限制，但是通过大量的实验证明，该方法同时对基空间和特征系数做稀疏性限制时，算法无法收敛到局部最小，因此该方法只能在两种稀疏性限制中任意选择一种．算法采用投影梯度下降法来实现，步长选择要足够小以确保目标函数每一步都在递减．NMFSC方法的迭代规则为［9］:

1)如果对基空间W加稀疏性限制，W=W－μW(WH－V)HT，然后将W的每一列做投影，使其为非负，且保证W的每一列稀疏性为Sw，那么H的标准乘法迭代公式为

规则中，μW，μH为迭代步长，且均为大于零的常量．

3 实验结果

3．1 实验数据

本实验采用北京科技大学的24人人耳图像库，每人10幅图像，包括4幅无遮挡图像(如图1(a)所示)和6幅遮挡图像(如图1(b)所示)，无遮挡图像有光照和角度的变化，其中第1幅图和第4幅图反映光照变化，第2幅图和第3幅图分别为旋转+30°和－30°的图像，反映角度变化．遮挡图像由左至右分别为轻微遮挡，次轻微遮挡和正常遮挡3种．

图1 人耳图像Fig．1 Ear images

3．2 实验结果及分析

本实验目的在于考察上述方法基于局部特征表示的特点，因此实验过程中选用每位志愿者的4幅无遮挡人耳图像作训练，6幅遮挡人耳图像做测试，分别采用上述方法得到训练集和测试集的特征向量，利用距离分类器进行分类，由于测试集所选图像均为遮挡图像，所以识别率普遍较低．图2显示了5种方法的识别率，图3显示了利用5种方法获得的特征空间H的稀疏性(其中NMF包括NMFSE和NMFDIV两种情况，NNSC和NMFSC分别包括Sw=0．5和Sw=0．7两种情况;*实线代表NMFSE，□实线代表NMFDIV，◇实线代表LNMF，☆实线代表Sw=0．7的NNSC，○虚线代表Sw=0．5的NNSC;+实线代表SNMF，×实线代表Sw=0．7 的 NMFSC，※虚线代表 Sw=0．5 的 NMFSC)．

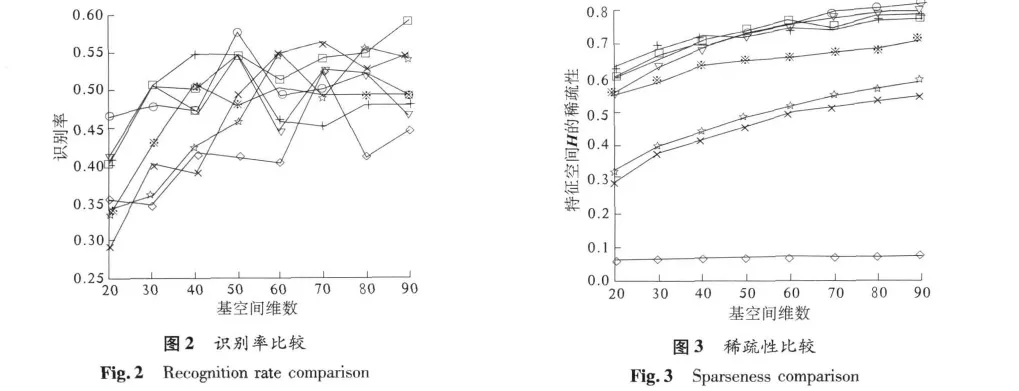
从实验结果可以看出，上述5种方法在基空间W高维范围内均得到了比较好的识别率，说明应用NMF相关算法进行局部遮挡情况下的人耳识别是有效的．特征空间H的稀疏性总体趋势是随着基空间W维数的增加而增大，而高的特征空间稀疏性可以加大样本间的特征差异，更加有利于识别分类，因此识别率在高维基空间范围总体较高．NMFSC方法中，基空间W的稀疏性为0．5时，特征空间H的稀疏性要高于基空间W稀疏性为0．7时，并且识别率的总体情况也优于基空间W稀疏性为0．7时，主要是由于NMFSC方法无法同时满足基空间W和特征空间H的稀疏性为最优．因此，为了获得更高的特征空间H的稀疏性和更好的识别率，可以适当降低基空间W的稀疏性，这也为遮挡情况下的人耳识别提供了有价值的启示．

4 结论

为了体现NMF方法基于局部特征的特点，本文将NMF以及在其基础上改进的几种非负矩阵因子算法应用于遮挡条件下的人耳识别．通过实验验证，得到了比较理想的结果，证明了NMF方法应用于遮挡情况下人耳识别的可行性和有效性．下一步工作是研究并提出效果更加理想的相关NMF遮挡人耳识别方法．

［1］ 马怡然，张凤玲．基于DCT的PCA及神经网络的人脸识别研究［J］．郑州大学学报:理学版，2007，39(3):76－79．

［2］ Boulgouris N V，Chi Z X．Gait recognition using radon transform and linear discriminant analysis［J］．IEEE Trans on Image Processing，2007，16(3):731－740．

［3］ Calhoun V D，Adali T．Unmixing fMRI with independent component analysis［J］．IEEE Engineering in Medicine and Biology Magazine，2006，25(2):79－90．

［4］ Arca S，Campadelli P，Lanzarotti R．A face recognition system based on local feature analysis［C］//The Conference on Audio and Video Based Biometric Person Authentication．Guildford，2003．

［5］ Lee D D，Seung H S．Learning the parts of objects by non-negative matrix factorization［J］．Nature，1999，401(6755):788 －791．

［6］ Oh H J，Lee K M，Lee S U，et al．Occlusion invariant face recognition using selective LNMF basis images［C］//Asian Conference on Computer Vision．Berlin，2006．

［7］ Hoyer P O．Non-negative sparse coding［C］//The 12th IEEE Workshop on Neural Networks for Signal Processing．Martigny，2002．

［8］ Yuan Yuan，Li Xuelong，Pang Yanwei，et al．Binary sparse non-negative matrix factorization［J］．IEEE Trans on Circuits and Systems for Video Technology，2009，19(5):772－777．

［9］ Liu Weixiang，Zheng Nanning，Lu Xiaofeng．Non-negative matrix factorization for visual coding［C］//IEEE International Conference on Acoustics，Speech and Signal Processing．Hong Kong，2003．