新型耗能增强型形状记忆合金阻尼器减震性能研究＊

陈 云，吕西林，蒋欢军

（同济大学土木工程防灾国家重点实验室，上海 200092）

形状记忆合金（shape memory alloys，简称SMA）是一种机敏材料，主要有两个特性：形状记忆性能和超弹性性能［1］.利用SMA的形状记忆性能可制作成驱动元件，进行结构主动控制，利用SMA的超弹性性能和高阻尼特性可制成各种构造形式的SMA阻尼器，进行结构被动控制.相比较其他类型的阻尼器，SMA阻尼器的一个突出优点是阻尼器耗能后残余变形很小.

目前开发的SMA阻尼器种类较多，大多数阻尼器是用SMA丝（SMA束或SMA绞线）制成.Tamai等［2］把SMA丝设置在框架的对角进行振动控制，并研究了其耗能性能；Corbi［3］提出了把SMA拉索设置在剪切框架的底部对角进行隔震，研究表明能有效地减小结构的动力反应，增大结构的自复位能力；丁阳等［4］通过数值模拟的方法研究了高层钢结构地震反应SMA对角拉索控制效果；韩玉林等［5］通过试验研究了把SMA拉索设置在框架对角的控制效果，研究表明设置了SMA拉索的框架振动反应衰减较快.

利用SMA制成各种构造形式的阻尼器也很多，Li Hui等［6］利用SMA超弹性特性开发了2种新型的SMA阻尼器——拉伸型SMA阻尼器和剪刀型SMA阻尼器，其中剪刀型SMA阻尼器通过改变剪刀的力臂可以达到位移放大的效果；Dolce等［7］设计了一种具有自复位能力的阻尼器；Zhang等［8］采用超弹性SMA铰线设计了一种可以重复使用的迟滞阻尼器（RHD）；Zuo等［9］提出了一种SMA复合摩擦阻尼器；薛素铎等［10－12］设计了几种不同类型的SMA阻尼器；Song等［13］比较详细地总结了SMA阻尼器在土木工程中的若干应用；李宏男等［14－15］也开发了几种SMA阻尼器；禹奇才等［16］提出了一种放大位移型SMA阻尼器；倪立峰等［17］也提出了SMA阻尼器；凌育洪等［18］也研发了一种新型SMA阻尼器.总之，目前开发的SMA阻尼器种类较多，但大多数不具备放大SMA位移反应的功能.为此，本文研究思路是首先通过材性试验研究了SMA丝滞回性能并确定了计算所需的SMA参数，提出一种SMA阻尼器，阐述了其设计要点，推导了恢复力模型，最后通过算例对比研究了SMA阻尼器的减震性能.

1 SMA的力学性能

鉴于随后要对SMA阻尼器在有限元程序里进行模拟计算，需要预先确定SMA的输入参数，特对SMA进行力学性能试验.

试验选用的SMA为Ti－50.8%Ni的SMA丝.SMA丝的最大可回复应变为8%，最大回复应力为600MPa.试件有效长度为150mm，直径为1.0 mm.拉伸试验装置为微机控制电子万能试验机，采用50mm标距的引伸仪测量位移.

试验时首先在室温下进行拉伸、卸载循环试验，使材料的超弹性性能稳定，然后开始加载、卸载，绘制应力－应变曲线.将试验所得SMA的应力应变曲线等效拟合后得到的应力应变曲线如图1所示，SMA的弹性模量为58 000N／mm2，泊松比取0.3，在程序里SMA的超弹性性能曲线被简化成多段线性直线，其拟合参数取值如表1所示.

图1 等效线性化的SMA应力应变曲线Fig.1 Equivalent linear stress－strain curves

表1 拟合曲线参数的取值Tab.1 The parameters of fitting curve

阻尼器安装在结构中所耗散能量的大小既与阻尼器自身的性能有关，也与阻尼器安装位置处结构的相对变形大小有关.因此，在阻尼器已经确定的前提下，如何在结构相对变形合理的情况下增大阻尼器的位移行程就是一个有意义的问题.本文所开发的SMA阻尼器可以放大SMA丝的变形，在同样结构变形的条件下，该阻尼器可以耗散更多的能量.

其依据是杠杆原理和平行四边形形状可以改变的性质.阻尼器主要由4根钢杆和两组SMA丝（束或绞线）组成，4根钢杆分成两组，每组两根钢杆之间通过销栓组成一个剪刀撑，SMA丝固定在剪刀撑较长一端的端部，两个剪刀撑较短一侧的端头之间通过销栓连接在一起组成一个平行四边形.阻尼器通过两根斜撑与结构的对角位置铰接在一起.其构造示意图如图2所示.

2 SMA阻尼器的设计方法

2.1 SMA阻尼器的设计要点

1）在图3中，安装SMA阻尼器的框架区格中，阻尼器剪刀撑的两个短边之比应与梁的跨度与柱高之比相等，即

2）阻尼器的每根钢杆在铰接连接的位置处被分成两部分，其中钢杆较长的部分与较短的部分之比应相等，即＝n，n应大于1，这样才能发挥位移放大的作用.

3）阻尼器的4根钢杆之间通过销栓连接成一个可以自由转动的机构.

4）阻尼器的SMA丝应张拉至其最大可恢复应变的一半左右.

5）斜撑的一端与阻尼器铰接在一起，另一端与框架铰接在一起.

满足以上要求，可以尽可能使斜撑的受力方向与SMA丝的拉力方向平行，两组SMA丝位移放大n倍.

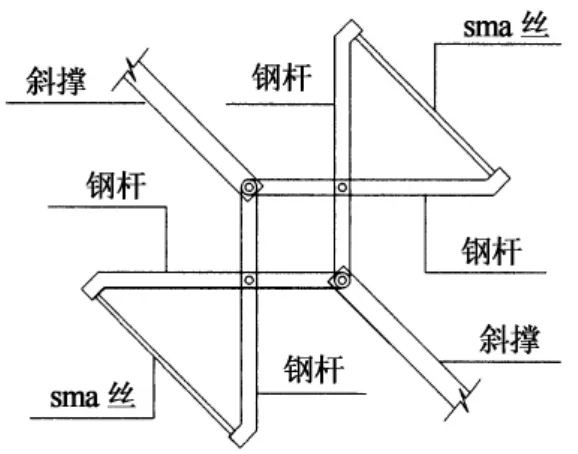
图2 新型SMA阻尼器构造示意图Fig.2 Design of new SMA dampers

图3 SMA阻尼器详图和安装示意图Fig.3 Design detail and installation of new SMA dampers

2.2 SMA阻尼器的恢复力模型

根据2.1的第5条，可知两根斜撑均为二力杆，故只考虑其轴力，不考虑剪力和弯矩.

在图3中，以整个阻尼器为研究对象（受力图略），则其受到两个力的作用，即两根斜撑的轴力，由二力平衡定理可知，两根斜撑的轴力大小相等，方向相反，作用线通过DE.

在图3中，以一个剪刀撑为受力对象，取隔离体如图4所示.

图4 剪刀撑的隔离体图Fig.4 The force analysis of components

可得FDEL＝FEDL，力作用线通过DE，平行AB.

在图3中，取钢杆AE为隔离体如5所示.

图5 钢杆的隔离体图Fig.5 The force analysis of components

FSMA的作用线平行FEDL，对C点取矩，即∑M（C）＝0，得：

同理可得在节点E右侧有如下等式，FEDR含义见图6.

在图3中，取节点E作为研究对象，如图6所示.

图6 节点的隔离体图Fig.6 The force analysis of node

因此，撑杆的受力：

对式（3）稍作变换即可得到SMA阻尼器的恢复力模型.

假定SMA丝的本构模型为：

式中x表示SMA丝的长度变化.

若SMA阻尼器在力作用下产生的相对位移用u表示，则由2.1设计要点2）可得：

把等式（4）和（5）代入等式（3）得：

式（6）所表示的F－u关系等式就是阻尼器的恢复力力学模型，它既与SMA丝的本构模型有关，也与阻尼器的位移放大倍数n有关.

3 算例分析

为了对阻尼器的减震性能进行研究验证，特别设计了3个计算模型，一个为普通的钢框架（简称无控结构），一个在普通钢框架底层中跨对角设置了两根SMA拉索（简称对角拉索控制结构），一个在普通钢框架的底层中跨对角设置了SMA阻尼器（简称SMA阻尼器控制结构）.拟通过低周反复分析和动力时程弹塑性分析研究其抗震性能.

3.1 模型设计

无控结构为一榀3层3跨钢框架，钢材的屈服强度为235MPa.结构模型参数如图7所示.

图7 模型结构图Fig.7 Model structure

对角拉索控制结构和SMA阻尼器控制结构设置2根相同的SMA拉索，每根拉索的等效截面面积为113mm2，计算参数完全相同，均如表1所示.

在图3中，经过设计计算，取SMA阻尼器位移放大倍数n＝2，SMA阻尼器的尺寸为：AC＝FG＝2 000mm，BC＝FH＝1 400mm，CD＝EF＝700mm，CE＝DF＝1 000mm，SMA拉索的长度为2 441mm.

在ansys有限元程序里对角拉索控制结构和SMA阻尼器控制结构的模型如图8和图9所示.

3.2 有限元模型参数

本文选用有限元程序ansys做计算分析，原因是ansys程序里的SMA本构模型可以比较精确地模拟SMA的超弹性特性.在程序里，SMA的超弹性恢复力曲线简化成多段线性曲线，曲线上的关键点根据SMA的拉伸试验拟合确定，如表1所示.计算时，需要输入的参数包括：SMA的弹模，泊松比，表1所示的确定SMA超弹性恢复力曲线的参数，还有一个表征SMA在拉压时不同反应的参数，可以在0.12～0.14之间取值.

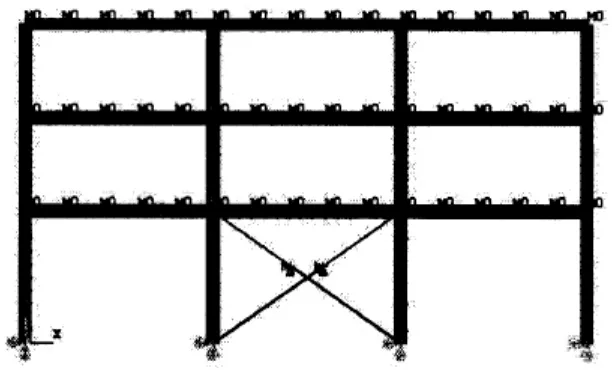
图8 对角拉索控制模型Fig.8 Diagonal SMA cables control model

图9 SMA阻尼器控制结构模型Fig.9 SMA dampers control model

SMA用solid185或solid186单元模拟.梁、柱和钢杆用beam188单元模拟，斜撑为二力杆，用link8单元模拟.为了实现钢杆组成的机构能够自由转动，需要对钢杆与钢杆、钢杆与撑杆的节点进行自由度耦合.mass21单元模拟每层的质量.

3.3 地震时程反应分析

3.3.1 地震波输入

模型结构位于8度Ⅳ类场地，设计地震分组为第1组.3个模型的质量分布完全相同，底层的质量为38t，二层32t，三层31t.阻尼器的耗能主要体现在中震和大震，基于更为关注阻尼器在大震下的性能，故在此仅对大震下的3个模型结构做计算分析比较.

根据场地条件及目的，选定3条地震波作为地震动输入，分别为El Centro地震波、Taft地震波和Pasadena地震波.

根据模态分析，无控结构、对角拉索控制结构和SMA阻尼器控制结构的基本周期分别为：0.615s，0.592s，0.548s.8度多遇地震的输入地震波的反应谱曲线与规范反应谱曲线如图10所示.通过频谱分析可知，El Centro波、Taft波和Pasadena波的卓越周期分别为0.56s，0.44s和0.38s.对比上述3种计算结构的基本自振周期可知，SMA阻尼器控制结构的基本周期与上述3条地震波的卓越周期最为接近，无控结构的基本周期与地震波的卓越周期相差较远，对角拉索控制结构在二者之间.时程分析时，结构的整体阻尼比取0.05.

图10 输入地震波的反应谱曲线与规范反应谱曲线Fig.10 Comparison of code response curve with input earthquake wave

3.3.2 地震响应分析结果

1）层位移和层间位移角控制效果

结构在地震作用下的层位移和层间位移角的大小是评价结构抗震性能的重要指标，定义结构的控制系数［19］如下所示：

式中βx为结构的振动控制系数；xo（t）为无控结构的动力反应峰值；xn（t）为有控结构的动力反应峰值.

图11～图13分别表示在El Centro波、Pasadena波和Taft波作用下3个结构的层位移和层间位移角.

图11 El Centro波作用下结构层位移和层间位移角Fig.11 Structural story drift and inter－story drift angle under El Centro seismic waves

在El Centro波作用下，SMA阻尼器控制结构的层位移和层间位移角都得到有效控制.由表2和表3可知，SMA阻尼器对结构底层层位移和层间位移角的控制效果分别达到了34.10%和33.97%，2层层位移和层间位移角的控制效果分别达到了23.62%和8.28%，3层层位移和层间位移角的控制效果分别达到了17.35%和4.72%，而对角拉索对结构层位移和层间位移角的最大控制效果仅为1.22%和7.55%.

图12 Pasadena波作用下结构层位移和层间位移角Fig.12 Structural story drift and inter－story drift angle under Pasadena seismic waves

图13 Taft波作用下结构层位移和层间位移角Fig.13 Structural story drift and inter－story drift angle under Taft seismic waves

表2 结构层间位移角控制效果Tab.2 Control effect of structural inter－story drift angle

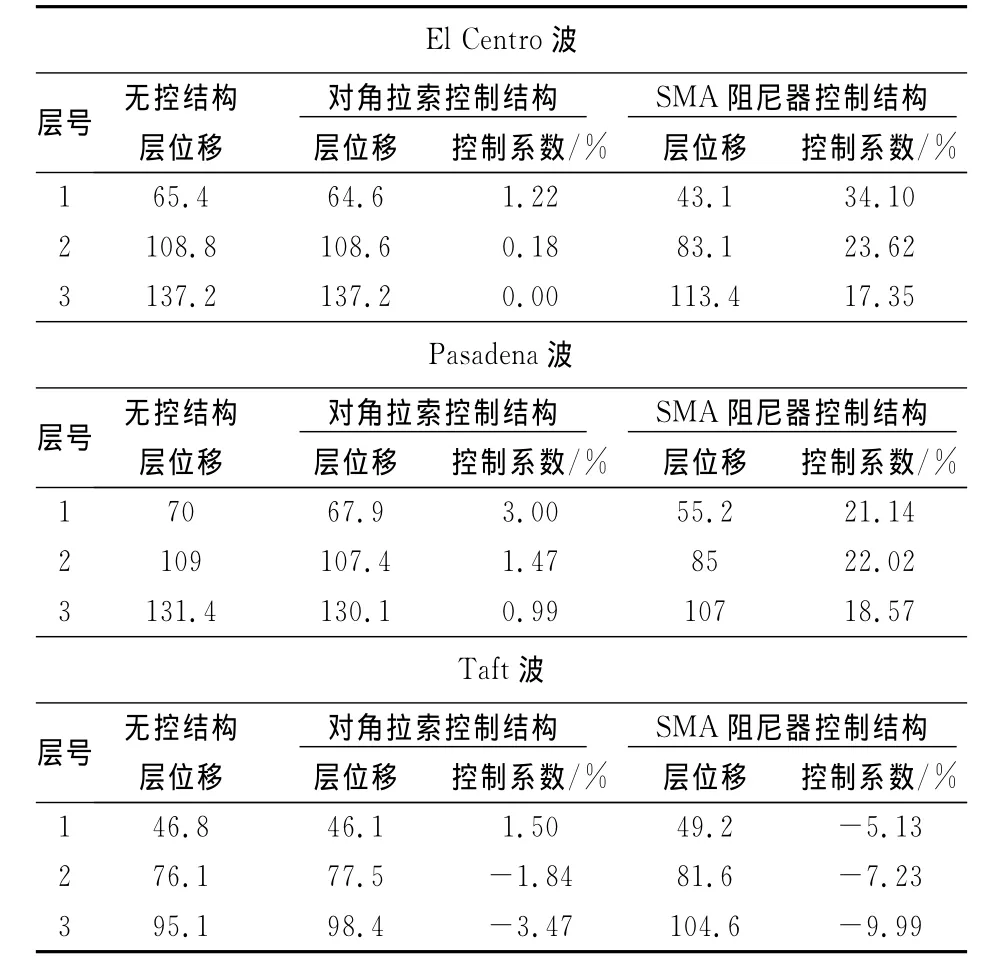
表3 结构层位移控制效果Tab.3 Control effect of structural story drift

在Pasadena波作用下，SMA阻尼器控制结构的层位移和层间位移角也能得到较好地控制，最大分别达到22.02%和20.96%，而对角拉索的控制效果最大仅为3.00%和2.99%，控制效果较差.

在Taft波作用下，除了3层的层间位移角控制效果较好外，SMA阻尼器控制结构和对角拉索控制结构的层位移和层间位移角大多数时候稍大于无控结构，最大不超过10%，原因可能是SMA阻尼器控制结构和对角拉索控制结构的基本周期接近Taft波的卓越周期导致的，但从随后的SMA拉索滞回耗能曲线可知，SMA阻尼器仍然发挥了较好的耗能作用.

对于SMA阻尼器控制结构，底层平均层间位移角为1／85，最大层间位移角为1／76，无控结构和对角拉索控制结构底层最大层间位移角分别达到1／60和1／62.

限于篇幅，仅列出El Centro波作用下顶层的位移时程反应，如图14所示.

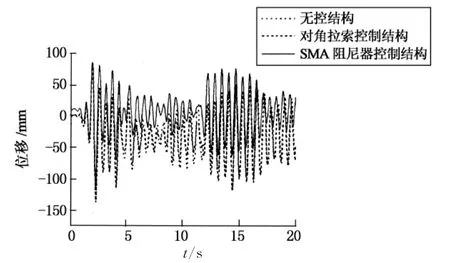
图14 El Centro波作用下结构顶层位移反应时程Fig.14 Structural top story drift response under El Centro waves

从图14可知，SMA阻尼器控制结构在大震下仍具备足够的恢复力，对角拉索控制结构和无控结构较早就屈服了，而且屈服比较严重，位移时程曲线过早偏离了平衡位置，此后一直远离平衡位置振动.与之相反，SMA阻尼器不仅减小了结构的峰值位移反应，并且能使位移很快衰减，减震效果明显.

2）层加速度控制效果

限于篇幅，仅列出El Centro波作用下顶层的加速度反应，如图15所示.

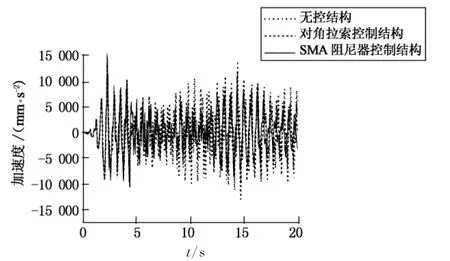
图15 El Centro波作用下结构顶层加速度反应时程Fig.15 Structural top story acceleration response under El Centro waves

在El Centro波作用下，无控结构的加速度峰值为13 918mm／s2，对角拉索控制结构的加速度峰值是13 779mm／s2，SMA阻尼器控制结构峰值为15 376mm／s2，SMA阻尼器控制结构的加速度反应最大，比无控结构大10%，对角拉索控制结构的加速度反应比无控结构稍小.

在Taft波作用下，无控结构的加速度峰值为13 801mm／s2，对角拉索控制结构的加速度峰值是12 709mm／s2，控制系数为7.9%，SMA阻尼器控制结构的加速度峰值是11 741mm／s2，控制系数为14.9%，SMA阻尼器的加速度控制效果较显著.

综合上述不同地震波作用下加速度反应，可以看出SMA拉索对加速度的控制效果有限，甚至可能会增大峰值加速度反应，尽管增大的幅度不超过10%，这和之前部分学者的研究结论也是相似的［16－17］，即SMA阻尼器对加速度的控制效果有限.另外一个原因是SMA阻尼器控制结构的基本周期最接近这3条波的卓越周期，因此可能导致对加速度的控制效果不佳.

3）层剪力控制效果

设置阻尼器后，结构的总层间剪力是结构层间剪力和阻尼器出力之和.从图16可知，无论SMA阻尼器控制结构还是对角拉索控制结构，结构1层和2层的总层间剪力都略大于无控结构.

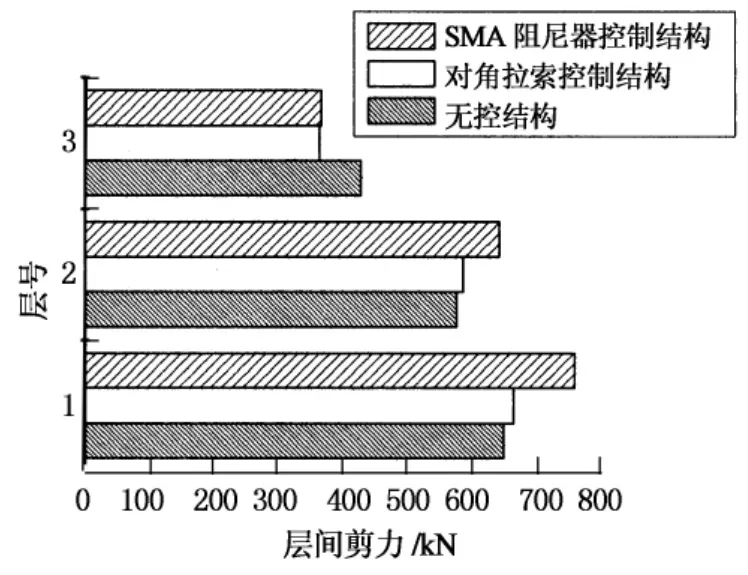
图16 El Centro波作用下结构总层间剪力Fig.16 Comparison of story shear under El Centro waves

在El Centro波作用下，无控结构的最大总层间剪力为649kN，SMA阻尼器控制结构的最大总层间剪力为759kN，增大的幅度达到16.9%，但除去阻尼器的出力后，结构构件承担的最大剪力为641kN，反而略小于无控结构.

在结构3层，SMA阻尼器控制结构和对角拉索控制结构的总层间剪力有所减小，SMA阻尼器控制结构的总层剪力减小了28.3%.总体来讲，有控结构的总层间剪力与无控结构相比略有增大，但有控结构的结构构件承担的剪力略小于无控结构.

4）SMA拉索滞回反应

从图17可知，SMA阻尼器控制结构和对角拉索控制结构的SMA拉索都始终处于受拉状态，其初始应变均为其总应变的一半左右，而且在整个震动过程中，SMA拉索的应变大于1%，小于8%，表明SMA拉索既没有松弛也没有拉断，实现了设计目的.

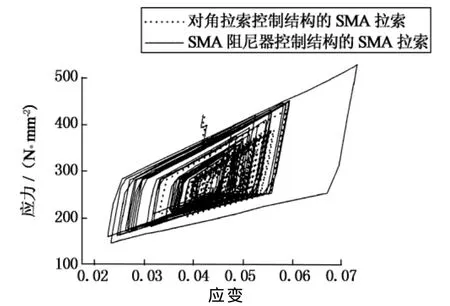
图17 El Centro波作用下SMA滞回耗能曲线比较Fig.17 Comparison of SMA hysteretic energy curves under El Centro waves

其次，比较图中两个结构SMA拉索的滞回环可以明显看出，SMA阻尼器控制结构中SMA拉索的滞回环非常饱满，而对角拉索控制结构的SMA滞回环窄了很多.在3条波的分别作用下，前者的应变范围平均达到1.5%～7.5%，后者的应变范围仅为3.2%～5.8%，前者应变幅度平均增大了2倍左右；比较应力的变化范围，前者的应力变化范围平均为127～528N／mm2，后者的应力变化范围为181～423N／mm2，应力幅度平均增大了1.66倍左右，进一步表明SMA阻尼器具有显著增强耗能的作用.

有限元分析得到的SMA拉索的滞回环与实测的SMA应力－应变曲线的形状基本一致，表明有限元程序里SMA的本构模型能较好地模拟SMA的超弹性性能.

4 结 论

本文首先通过材性试验研究了SMA丝材的超弹性变形性能和参数取值，然后提出了一种耗能增强型SMA阻尼器，阐述了其构造和工作原理，推导了其恢复力模型，最后通过对比研究进行了地震时程分析，得出以下初步结论：

1）SMA材性试验表明，SMA的滞回环较饱满，超弹性变形性能较好.在实际应用时可将其等效为多线性模型，分析表明与程序中的超弹性本构吻合较好.

2）地震时程分析表明，该SMA阻尼器对结构的层位移和层间位移角具有显著控制效果，最大控制效果分别达到了34.1%和33.97%，而对角SMA拉索对结构层位移和层间位移角控制效果一般；SMA阻尼器和对角SMA拉索相同，对结构加速度反应控制效果一般，设置SMA阻尼器和对角SMA拉索后结构构件承受的层间剪力略有减小.

3）SMA阻尼器中SMA拉索滞回环非常饱满，通过其位移放大作用，SMA拉索的耗能能力能够充分发挥，相反对角SMA拉索滞回环较窄，导致SMA拉索的耗能能力未能得到充分发挥.

4）从经济价值上考量，制约SMA大规模应用的一个障碍是SMA的价格较贵，因此必须充分利用其价值，对角SMA拉索和本文的SMA阻尼器使用了同样重量的SMA丝，但控制效果却远胜前者，因此其经济价值较大，有助于SMA在结构振动控制中的推广应用.

［1］ 王社良.形状记忆合金在结构控制中的应用［M］.西安：陕西科学技术出版社，2000：5－33.WANG She－liang.The application of shape memory alloys in structural vibration control［M］.Xi’an：Shaanxi Science and Technology Press，2000：5－33.（In Chinese）

［2］ TAMAI H，KITAGAWA Y.Pseudoelastic behavior of shape memory alloy wires and its application to seismic resistance member for building［J］.Computational Materials Science，2002，25：218－227.

［3］ CORBI O.Shape memory alloys and their application in structural oscillations attenuation［J］.Simulation Modeling Practice and Theory，2003，11：387－402.

［4］ 丁阳，张笈玮.高层钢结构地震反应形状记忆合金拉索控制研究［J］.地震工程与工程振动，2005，25（3）：152－157.DING Yang，ZHANG Ji－wei.Seismic response control of tall steel structures using shape memory alloy tendons［J］.Journal of Earthquake Engineering and Engineering Vibration，2005，25（3）：152－157.（In Chinese）

［5］ 韩玉林，李爱群，林萍华，等.基于形状记忆合金耗能器的框架振动控制试验研究［J］.东南大学学报：自然科学版，2000，30（4）：16－20.HAN Yu－lin，LI Ai－qun，LIN Ping－hua，et al.Experimental study of frame structure vibration control by using shape memory alloy damper［J］.Journal of Southeast University：Natural Science，2000，30（4）：16－20.（In Chinese）

［6］ LI Hui，MAO Chen－xi，QU Jin－ping.Experimental and theoretical study on two types of shape memory alloy devices［J］.Earthquake Engineering and Structural Dynamics，2008，37：407－426.

［7］ DOLCE M，CARDONE D，MARNETTO R.Implementation and testing of passive control devices based on shape memory alloys［J］.Earthquake Engineering and Structural Dynamics，2000，29：945－968.

［8］ ZHANG Y，ZHU S.A shape memory alloy based reusable hysteretic damper for seismic hazard mitigation［J］.Smart Materials and Structures，2007，16：1603－1613.

［9］ ZUO Xiao－bao，CHANG Wei，LI Ai－qun，et al.Design and experimental investigation of a super elastic SMA damper［J］.Materials Science and Engineering：A，2006，438／439／440：1150－1153.

［10］薛素铎，董军辉，卞晓芳，等.一种新型形状记忆合金阻尼器［J］.建筑结构学报，2005，26（3）：45－50.XUE Su－duo，DONG Jun－hui，BIAN Xiao－fang，et al.A new type of shape memory alloy damper［J］.Journal of Building Structures，2005，26（3）：45－50.（In Chinese）

［11］薛素铎，石光磊，庄鹏.SMA复合摩擦阻尼器性能的试验研究［J］.地震工程与工程振动，2007，27（2）：145－151.XUE Su－duo，SHI Guang－lei，ZHUANG Peng.Performance testing of SMA incorporated friction dampers［J］.Earthquake Engineering and Engineering Vibration，2007，27（2）：145－151.（In Chinese）

［12］薛素铎，庄鹏，李彬双.SMA－橡胶支座的力学性能试验研究［J］.世界地震工程，2005，21（4）：10－15.XUE Su－duo，ZHUANG Peng，LI Bin－shuang.Experimental study on mechanical behavior of SMA－rubber bearing［J］.World Earthquake Engineering，2005，21（4）：10－15.（In Chinese）

［13］SONG G，MA N，LI H N.Applications of shape memory alloys in civil structures［J］.Engineering Structures，2006：1266－1274.

［14］李宏男，钱辉，宋钢兵.一种新型SMA阻尼器的试验和数值模拟研究［J］.振动工程学报，2008，21（2）：179－184.LI Hong－nan，QIAN Hui，SONG Gang－bing.A new type of shape memory alloy damper：design experiment and numerical simulation［J］.Journal of Vibration Engineering，2008，21（2）：179－184.（In Chinese）

［15］REN W J，LI H N，SONG G B.Design and numerical evaluation of an innovative multi－directional shape memory alloy damper［C］／／Proceedings of Active and Passive Smart Structures and Integrated Systems.Bellingham：SPIE，2007.

［16］禹奇才，刘春晖，刘爱荣.一种放大位移型SMA阻尼器的减震控制分析［J］.地震工程与工程振动，2008，28（5）：151－156.YU Qi－cai，LIU Chun－hui，LIU Ai－rong.The analysis of structure vibration control by using shape memory alloy dampers with magnifying story drift［J］.Journal of Earthquake Engineering and Engineering Vibration，2008，28（5）：151－156.（In Chinese）

［17］倪立峰，李秋胜，李爱群，等.新型形状记忆合金阻尼器的试验研究［J］.地震工程与工程振动，2002，22（3）：145－148.NI Li－feng，LI Qiu－sheng，LI Ai－qun，et al.Investigation and experiment of damper based on shape memory alloy（SMA）［J］.Earthquake Engineering and Engineering Vibration，2002，22（3）：145－148.（In Chinese）

［18］凌育洪，彭辉鸿，张帅.一种新型SMA阻尼器及其减震性能［J］.华南理工大学学报：自然科学版，2011，39（6）：119－125.LING Yu－hong，PENG Hui－hong，ZHANG Shuai.A novel SMA damper and its vibration reduction performance［J］.Journal of South China University of Technology：Natural Science，2011，39（6）：119－125.（In Chinese）

［19］吕西林.复杂高层建筑结构抗震理论与应用［M］.北京：科学出版社，2007：315－323.LV Xi－lin.Seismic theory and application for complex high－rise structures［M］.Beijing：Science Press，2007：315－323.（In Chinese）