关于凸函数的有趣不等式

刘小宁

(武汉软件工程职业学院，湖北武汉430205)

探索与建立新的不等式，是数学界长期的研究课题之一［1－2］。文中根据凸函数定理［3］，基于文献［4］的研究，得到关于凸函数的有趣不等式，以期与同行一起探索得到新的不等式。

1 凸函数定理

为讨论方便，文中约定i、n为正整数，1≤i≤n。

定义:若函数f(x)在定义域内有f(x)≤0，则f(x)为上凸函数;若有f(x)≥0，则f(x)为下凸函数。

凸函数定理［3］:若 pi＞ 0，xi为上凸函数 f(x)在定义域内的点，则有

等号当且仅当x1=x2=… =xn时成立。

当f(x)为下凸函数时，式(1)的不等号反向。

2 有趣的不等式

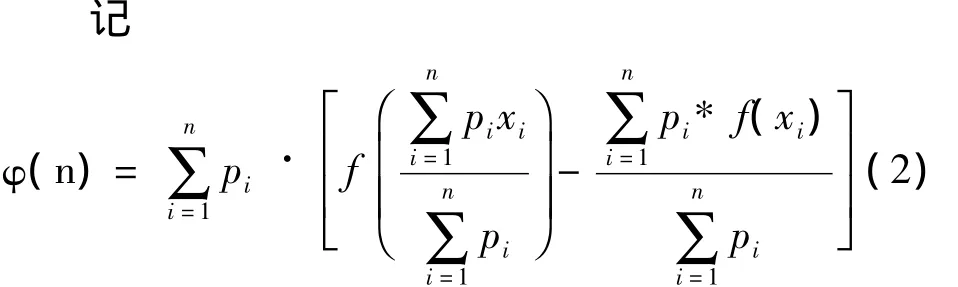
定理:若pi＞0，xi为上凸函数f(x)在定义域内的点，则有

证明:对于上凸函数f(x)在定义域内的点xi与yi作如下变换:当1≤i≤n－1时，

当i=n时，yn=xn;对于yi应用凸函数定理可得:

由式(2)与式(4)可知式(3)成立，证毕。

特别是当f(x)为下凸函数时，式(3)的不等号反向。

定理是关于凸函数的有趣不等式，即在变量的定义域内，不等式只与变量个数有关而与变量大小无关;显然定理是此类不等式的推广［4－8］。

注意到φ(n)≥φ(1)=0，由式(3)可得到式(1)，因此可认为式(3)是凸函数定理的加细。

3 应用

例1:对于上凸函数f(x)及定义域内的点xi，函数

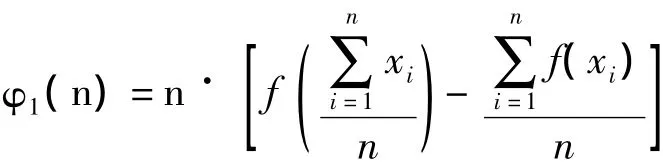
是n的递增函数。

证明:取定理中pi=1或pi=1/n，可得例1，证毕。

例2:若pi＞0，xi＞0，则加权均商函数是n的递增函数。

证明:取f(x)=lnx，因f(x)=－x－2＜ 0，故f(x)为上凸函数，由定理可知:φ(n)≥φ(n－1)，有

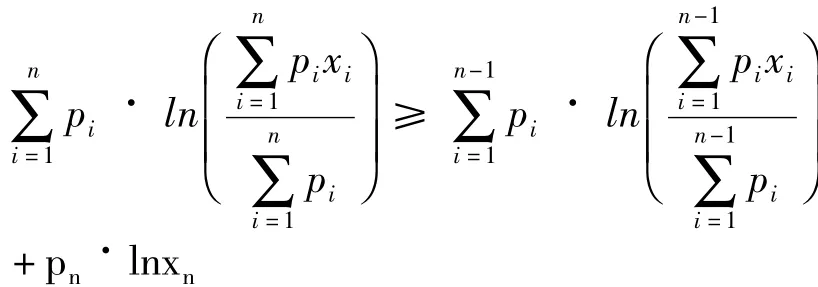
将上式变形可得 φ3(n)≥ φ3(n－1)，故φ3(n)是n的递增函数，证毕。

注意到φ3(n)≥φ3(1)=1，由例2可得

推论1:若pi＞ 0，xi＞ 0，有

等号当且仅当x1=x2=… =xn时成立。

推论1是著名的算术－几何加权平均值不等式［3］。

在例2中取pi=1与pi=1/n，可得

推论2:若xi＞0，则均商函数

是n的递增函数。

例3:若pi＞0，xi＞0，则加权均差函数

是n的递增函数。

证明:对于正数pi与yi，由推论1可得

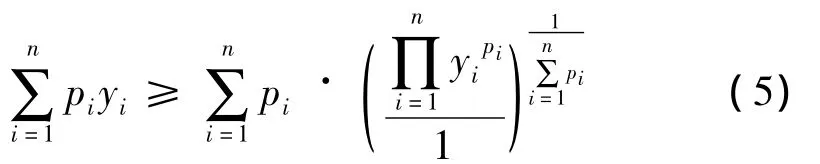
对于正数xi与yi作如下变换:当1≤i≤n－1时，

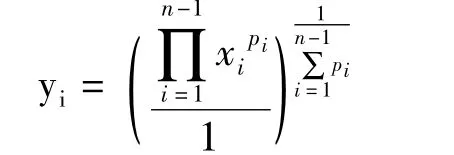
当i=n时，yn=xn;由式(5)可得:

将上式变形可得 φ6(n)≥ φ6(n－1)，故φ6(n)是n的递增函数，证毕。

注意到φ6(n)≥φ6(1)=0，由例3也可得到著名的算术－几何加权平均值不等式，即得到推论1。

在例3中取pi=1与pi=1/n，可得

推论3:若xi＞0，则均差函数

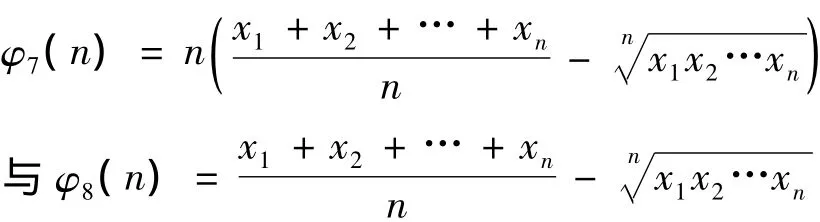
是n的递增函数。

［1］匡继昌.常用不等式［M］济南:山东科学技术出版社，2010(第4版).

［2］邓寿才.数学奥林匹克不等式散论［M］.哈尔滨:哈尔滨工业大学出版社，2011.

［3］徐利治，王兴华.数学分析的方法及例题选讲［M］.北京:高等教育出版社，1984(修订版).

［4］刘小宁.凸函数的一个有趣性质［J］.中学数学月刊，1983(02):42～43.

［5］刘小宁.平均值不等式的又一证法——兼谈均商函数的递增性［J］.数学通讯，1995(07):23 ～24.

［6］郭莉.加权均差(商)函数单调性新证［J］.毕节学院学报，1999，17(3):20 ～24.

［7］刘小宁.关于变量个数的几个单调函数［J］.数学通讯，2003(09):31.

［8］刘小宁.涉及变量个数的两个不等式［J］.武汉工程职业技术学院学报，2012，24(2):61～62.