基于混合蚁群算法的“多日游”路线优化问题

杨丽馨

（唐山市第十二中学，河北 唐山 063000）

基于混合蚁群算法的“多日游”路线优化问题

杨丽馨

（唐山市第十二中学，河北 唐山 063000）

针对“多日游”路线优化问题，提出了一种新的混合蚁群算法，并建立了“多日游”旅游交通路线的数学模型。通过多次实验和计算，证明将混合蚁群算法运用于“多日游”旅游交通线路，可以有效求得问题的最优解或近似最优解，并以秦皇岛地区各旅游景点为例进行了分析。

“多日游”旅游交通路线；混合蚁群算法；路径优化

“多日游”旅游交通路线优化问题的研究在旅游研究领域中具有十分重要的理论和现实意义。在旅游企业中，找到一组费用最小、旅游景点最多的旅游路径，可有效降低成本、提高服务效益并增加总体经济效益，因此，采取科学合理的方法确定旅游路线是一项非常重要的工作。蚁群算法是一种来自大自然的随机搜索寻优方法，是生物界的群体启发行为，现已应用于组合优化、人工智能等多个领域。蚁群算法的正反馈性和协同性使其可用于分布式系统，隐含的并行性使之具有极强的发展潜力。已有文献[1,2]用蚁群算法对“多日游”路线优化问题进行了研究并取得较好的效果。本文在前人研究的基础上，将混合蚁群算法用于多日游路线优化问题，以期为旅游企业的决策提供理论指导。

1 混合蚁群算法原理

本文蚁群算法是以TSP（旅行商问题）的蚁群算法为基础，充分考虑VRP（车辆路径问题）的具体要求，并在此基础上对算法的选择机制、更新机制以及协调机制做进一步改进，引入自适应的转移策略和信息素更新策略，并融合大洪水算法、节约法等方法，以克服蚁群算法计算时间长、易出现停滞的缺陷[3-5]。

1.1 混合蚁群算法设计

1.1.1 算法基本规则[6-8]

1.1.1.1 转移规则

借鉴Dorigo的Ant-Q算法思想，采用确定性选择和随机性选择相结合的转移策略。

1.1.1.2 信息素更新规则[9]

信息素更新采用局部更新和全局更新相结合的策略。

1）局部更新规则

定义1 设经过结点i的蚂蚁数为R，经过有向边(i, j)的蚂蚁数为r，则称r/R为边(i, j)的蚂蚁吸引力。

在进行信息素局部更新时，若每次施放的信息素量Q为常量，则(i, j)的蚂蚁吸引力越大，经过边(i, j)的蚂蚁相对其它的边来说数量越多，从而局部更新的次数就越多，久而久之，会导致边之间的信息素量差距过大，限制算法搜索的全局性。Q值也会影响算法的搜索效率，Q值过大会使算法易收敛于局部极小值，过小又会影响算法的收敛速度。随着算法搜索状态的变化，Q值也应该不断调整，调整的原则是，边的吸引力越大，t时刻的信息素量Q(t)越小，不妨设Q(t) = Q(1-r/R)，t为时刻。

假设第k只蚂蚁在第nc次迭代周期中的第f次转移时经过边(i, j)，在此之前共有Rk只蚂蚁经过i点，其中有rk只蚂蚁选择了边(i, j)，于是得到算法的局部更新规则如下：

2）全局更新规则

在所有蚂蚁均构造完路径后，对所有可行解以及迄今为止最优解的边进行全局信息素更新。采取的规则如下

p2p当(i, j) ∈L*时，Δ=Q3D( L*)，否则Δτ*ij=0。其中，D( Ap)表示第p个可行解的路径长度，D(L*)表示迄今为止最优解的路径长度；ρ2表示更新后信息素的挥发度；Q2、Q3分别表示对应时刻的信息素量；Ap为第p个可行解。

3）负反馈机制

蚁群算法的选择机制就是使好的路径以较大的概率选中，而正反馈机制又必然会促使这些路径在以后的选择中更具竞争优势。当搜索陷入局部最优解时，算法无法从局部极小值点跳出来，为此引入负反馈机制，包括：（1）借鉴MIN-MAX的思想，将各个路径上的信息量限定在某个固定的范围内，以便在一定程度上减少路径之间信息素浓度差距；（2）在全局更新时，加入负反馈信息量，即让Q2Q3<0，以减少该局部解所对应路径上的信息素量。

1.1.2 可行解问题

在VRP中，每只蚂蚁所构造的回路仅是可行解的一个组成部分，各蚂蚁所构造的回路可能组成一些可行解，但也可能一个可行解都得不到。如果得不到可行解，则该次迭代除施加了局部信息素影响外对最优解的搜索未有任何影响，若经常出现这种情况，则显然会浪费大量的计算时间。因此如何有效避免无可行解现象是算法设计的一个关键问题。可以采取以下策略：（1）大蚂蚁数策略。增加算法的蚂蚁数量M，扩大组合范围，从而增加可行解产生的可能性；（2）蚂蚁初始分布均匀策略。在每次迭代前，将蚂蚁随机均匀分布于各个结点，从而增加发现可行解的机会；（3）多周期蚂蚁组合策略。在蚂蚁数较少情况下，可以将本次迭代中各蚂蚁所产生的回路和往次未发现可行解的迭代（一次或多次）所产生的子回路进行组合；（4）近似解可行化策略。在找不到可行解的情况下，选择一些和可行解接近的非可行解作为问题的近似解，再按照某些规则（如节约法等）将近似解转变成可行解。当算法不存在可行解时，采取该策略显然可以保证获取至少一个可行解。

1.2 混和蚁群算法的步骤

混合蚁群算法求解VRP问题的步骤如下：

（1）初始化各参数，输入系统基础数据，设找到的最优解为L*，迭代计数器nc=0；

（2）将M个蚂蚁随机均匀地放到N个结点上，得到结点i的蚂蚁集Si和蚂蚁数bi，初始化蚂蚁k的已走点集tabuk以及候选点集allowedk；l表示已旅游完一天的蚂蚁数，l=0；初始点为0的蚂蚁的过程变量Pro[k]=1，初始点为非0点的蚂蚁的过程变量Pro[k]=2；

（3）在结点i取蚂蚁k，判断其初始结点。若为0点，按转移规则确定结点j，更新tabuk、Si、bi。并且若Pro[k]=1，则Pro[k]=2，转步骤3；而当Pro[k]=2时，若j点为初始结点，则l++，转步骤3；否则转步骤4。若为非0点，则按转移规则确定转移结点j，更新tabuk、Si、bi。并且当Pro[k]=1时，若j点为0，则Pro[k]=2，转步骤3；当Pro[k]=2时，若j点为初始结点，则l = l+1，转步骤3，否则转步骤4；

（4）更新Si，重复步骤3-4直到该结点的蚂蚁数量bi=0为止；

（5）重复步骤3-5，直到所有结点的bi=0；

（6）在所有蚂蚁都移动一次后，按局部更新规则对所有路径的信息素进行更新；

（7）更新所有结点的bi，若所有结点上蚂蚁数量bi=0或l = M，转下一步，否则转步骤3；

（8）由各蚂蚁的tabuk得到路径集

在L中寻找可行解，得到可行解集

若未发现可行解，实施多周期蚂蚁组合策略生成L-ch子回路集，再在L-ch中寻找可行解。若仍未发现可行解，则采取近似解可行化策略，转下一步。

（9）采用大洪水算法对可行解集A中各个可行解进行局部优化，得到A′，计算本次搜索到的最优路径L*(nc)，并得到迄今为止的最优路径，

L*=min{L*(nc),L*}，nc为迭代计数；

（10）若算法陷入停滞，采用负反馈机制调整路径上的信息素，并调大r0，否则按全局更新规则进行信息素的全局更新；

（11）判断nc是否等于最大迭代次数ncmax，若是，则算法终止，输出L*；否则，nc++，转步骤2。

2 实验及分析

2.1 实例仿真

设有20个旅游景点（JD）随机分布于边长为10 km的正方形区域内。休息地位于区域正中央，其坐标为(0, 0)。各旅游地游玩所需时间也由计算机随机产生，每天的游玩时间为9 h。基础数据如表1所示，其中tdp为单个景点游玩的时间（h）。

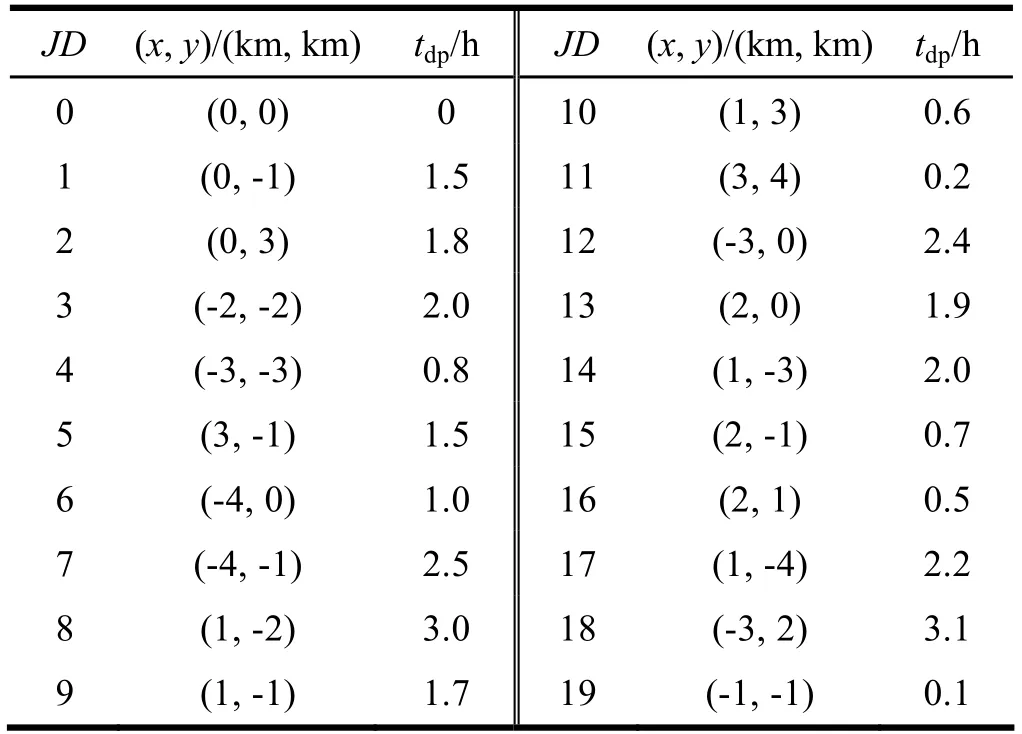
表1 实验基础数据

采用的参数为M=60，最多迭代次数ncmax=50，τij=10，游玩最多公里数MAX=100，游玩最少公里数MIN=2，α=1，β=1，γ=0.5，ρ1=0.85，ρ2=0.95，Q1=10，Q2=50，Q3=100，r0=1。运行10次，结果如表2所示，其中为平均最小行走距离（km），T为（游玩）所用天数（d），ncf为首次搜索终解代数，tc为计算用时（s），为行走距离与最小行走距离差（km）。

表2 实验计算结果

从表2可以看出，用蚁群算法的10次求解中，都得到了质量很高的解。其中最好解为41.86 km，路线1：0-18-0；路线2：0-1-17-14-8-0；路线3：0-12-6-7-4-3-19-0；路线4：0-2-10-11-16-13-5-15-9-0。蚁群算法的计算结果稳定，10次求解中最差解的游玩里程仅比最好解多5.8%。从计算效率看，10次求解的平均计算时间为2.14 s，计算效率较高，有效地解决了计算时间长的问题。从上述分析可见，对于VRP，利用蚁群算法可取得比较理想的结果，且计算结果稳定。

为了便于比较，分别用爬山法、遗传算法、模拟退火算法对该实例求解了10次，解的搜索次数都为15 000次，4种算法的计算结果见表3，其中Ddev为解的标准差。

表3 爬山法、遗传算法、模拟退火算法及蚁群算法比较

由表3不难看出，从寻优结果看，蚁群算法明显优于其它3种算法；从计算效率看，蚁群算法低于爬山算法和模拟退火算法，但高于遗传算法；从算法的稳健性看，蚁群算法计算结果的稳定性明显优于其它3种算法。

2.2 运行参数和算法策略对蚁群算法性能的影响

2.2.1 运行参数对蚁群算法搜索性能的影响

蚁群算法的运行参数主要有蚂蚁数M、基本信息素量τij、转移规则各相对重要性参数（α、β、γ、λ）、信息素的持久度（ρ1、ρ2）以及施放量（Q1、Q2、Q3）等。本文仅以蚂蚁数M为例讨论运行参数对算法搜索性能的影响。

对上述实例，分别取M =30、40、50、60、70、80、90、100，τij=20， ncmax=50， MAX=80， MIN=2，α=2，β=1，γ=0.5，λ=0.2，ρ1=0.85，ρ2=0.95，Q1=5，Q2=50，Q3=100，r0=1，各运行50次，结果如表4所示，其中为平均迭代步数。

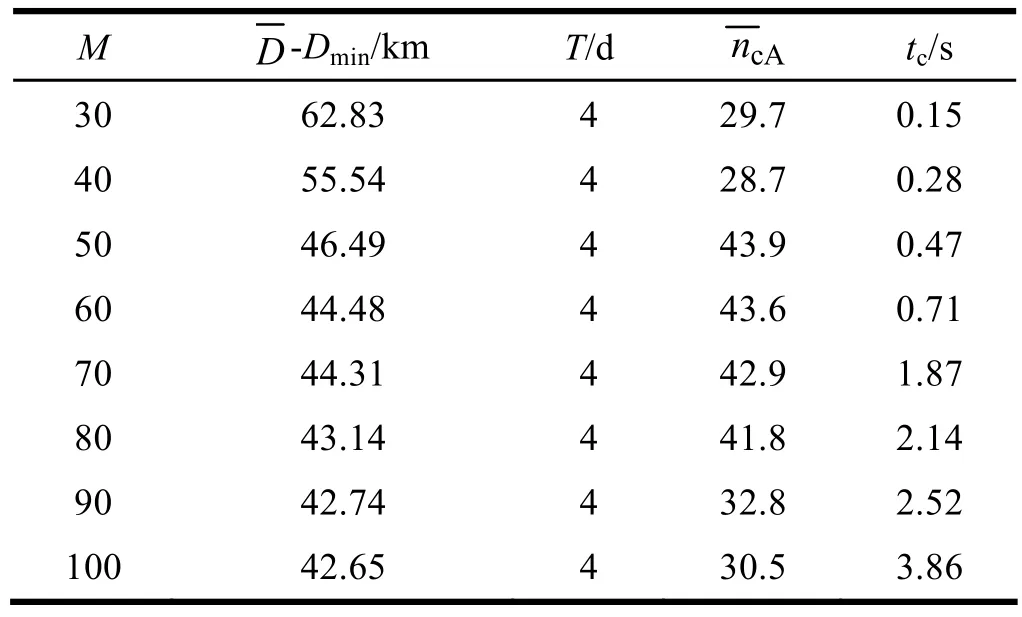
表4 蚂蚁数M对蚁群算法性能的影响分析表

由表4可以看出，蚂蚁数较大时，解的质量比较高，但随着蚂蚁数的不断增加，解的质量的提高越来越不明显，而计算时间却大幅度增加。因此就本实例而言，采用60～80个蚂蚁就可以了。

2.2.2 算法策略（SC）对蚁群算法搜索性能的影响

实验中发现，若不采取任何可行解获取策略，较大规模问题的蚁群算法基本发现不了可行解，因此对大蚂蚁数策略、蚂蚁初始分布均匀策略、多周期蚂蚁组合策略以及近似解可行化策略等4个策略以及它们之间的组合进行实验比较，具体分析6种算法：SC1，采取小蚂蚁数（M =40）和初始蚂蚁分布均匀策略；SC2，采取大蚂蚁数（M =80）和初始蚂蚁分布均匀策略；SC3，在SC1的基础上，增加多周期蚂蚁组合策略；SC4，在SC1的基础上，增加近似解可行化策略；SC5，在SC2的基础上，增加近似解可行化策略；SC6，在SC4的基础上，添加多周期蚂蚁组合策略。分别对前述实例求解，最大迭代次数为20，各运行20次，结果如表5所示，其中ncn为找不到解的迭代数，为平均无可行解数。

表5 算法策略对蚁群算法性能的影响分析表

由表5可见，SC3相对SC1而言，虽然计算时间稍长，但其求解质量有较大提高，而相对SC2而言，其计算结果和平均无可行解次数均比较接近，而计算时间却有较大幅度的节省。后3种算法由于引进了近似解可行化策略，因此不存在无可行解的问题。SC4的计算结果质量较前3者有很大提高。在各种算法中，计算结果最好的为SC5，其平均计算结果为43.13 km，离问题最好解41.86 km相当接近，其原因在于它既采用了大蚂蚁策略，又采用了近似解可行化策略，但计算时间也最长。

3 实例分析——秦皇岛地区“多日游”交通路线模型

3.1 模型建立

表6 实验基础数据

秦皇岛旅游区域内现有12个旅游景点，其基础数据如表6所示，休息地位于区域正中央的天下第一关，各景点游玩所需时间tdp（h）由实际估计得到。

3.2 模型求解

假设：（1）采用的运行参数为M=60，ncmax=50，τij=10，MAX=100，MIN=2，α=1，β=1，γ=0.5，ρ1=0.85，ρ2=0.95，Q1=10，Q2=50，Q3=100，r0=1；（2）每天的游玩时间为9 h；（3）运行10次。按上述混合蚁群算法计算，结果如表7所示。

表7 实验计算结果

从表7中可以看出，用蚁群算法的10次求解中，都得到了质量很高的解，其中最好解为83.72 km，路线1的行走路径为0-1-3-0；路线2为0-2-7-0；路线3的为0-8-6-0；路线4的为0-11-10-12-0；路线5的为0-9-5-4-0。蚁群算法的计算结果也较稳定，10次求解中，最差解的游玩里程仅比最好解多5.8%。从计算效率看，10次求解的平均计算时间为2.14 s，计算效率较高。可见，对于VRP，利用蚁群算法可取得比较理想的结果，且计算结果也较稳定。

4 结论

将蚁群算法引入到VRP中来，通过分析VRP与TSP的区别，构造了适于求解VRP的蚁群算法。为减少计算时间，避免算法停滞，对算法的选择机制、更新机制以及协调机制作了进一步研究，并融合了大洪水算法以及节约法等方法。在此基础上，本文所设计的自适应混合蚁群算法不但具有很强的发现较好解的能力，还具有较高的计算效率，计算结果相当稳定。

[1] 王大志,汪定伟,闫杨.一类多旅行商问题的计算及仿真分析[J].系统仿真学报,2009,21(20)∶6378-6381.

[2] 李伟,赵瑜.基于蚁群算法的“多日游”线路优化问题[J].

中国物流与采购,2009(10)∶76-77.

[3] 姜启源,谢金星,叶俊.数学模型[M].北京∶高等教育出版社,2003∶111-120.

[4] 李士勇.蚁群算法及其应用[M].哈尔滨工业大学出版社, 2004∶10-98.

[5] 马良,朱刚,宁爱兵.蚁群优化算法[M].科学出版社,2008∶35-112.

[6] 邢文训,谢金星.现代优化计算方法[M].清华大学出版社, 1999∶102-135.

[7] 高尚,杨静宇.群智能算法及其应用[M].水利水电出版社, 2006∶9-157.

[8] 雷德明,严新平.多目标智能优化算法及其应用[M].科学出版社,2009∶22-38.

[9] 刘任任.算法设计与分析[M].武汉理工大学出版社, 2003∶40-47.

（责任编辑、校对：赵光峰）

Optimization Problem about the Choice of “Multi-Day” Tourism Route Based on Hybrid Ant Colony Algorithm

YANG Li-xin

(Tangshan No.12 Middle School, Tangshan 063000, China)

For the “multi-day” line optimization, a new hybrid ant colony algorithm is proposed and a “multi-day” tourist traffic route model is established. Through experiments and calculations, it shows that the optimal solution or near optimal solution can be effectively obtained when the hybrid ant swarm algorithm is applied to the “multi-day” tourist traffic lines.

“multi-day” tourism route; hybrid ant colony algorithm; path optimization

F59

A

1009-9115(2013)05-0037-04

10.3969/j.issn.1009-9115.2013.05.011

2013-05-09

杨丽馨（1968-），女，唐山人，硕士，高级教师，研究方向为最优化。