焊接硬质合金枪钻钻削45钢的力学模型研究

（上海大学机电工程与自动化学院，上海200072）

焊接硬质合金枪钻钻削45钢的力学模型研究

贾文幸

（上海大学机电工程与自动化学院，上海200072）

研究了硬质合金枪钻钻削45钢的力学模型。通过对硬质合金枪钻主切削刃、导向支撑面、间隙面上的受力进行积分，借鉴特殊的能量模型并考虑了枪钻的几何结构参数、切削参数及工件的材料性能，建立了枪钻的力学模型。切削实验数据显示，枪钻所受力和力矩会随着切削进给的增加以及切削速度的降低而增加。

焊接硬质合金枪钻 力学模型 切削实验

1 引言

在100年前，枪钻最初用于钻削枪管[1]。如今，广泛应用于汽车行业的整体硬质合金枪钻，在钻削较深且精密的发动机曲轴孔时有比较好的性能[2]。研究钻削力学特性的常见方法有有限元分析和实验测量。Strenkowski用有限元方法分析了麻花钻钻削过程中的钻削力和扭矩[3]。同时，Griffiths在不同进给的条件下，测量了BTA钻头切削刃和支撑面的力[4]。Jung建立了一种枪钻的受力模型，考虑了支撑面的角度和侧面间隙对切削力的影响，推导出了力矩与轴向力公式，并利用了校准能量模型分析计算了主切削刃上的力[5]。枪钻的寿命以及孔加工的质量取决于刀具磨损、断屑和排屑[6]，Obikawa[7-8]、Hossainy[9]、Warnecke[10]、Yen[11]以及Li[12]等人已经对此做了研究。

切削参数是影响切削质量的重要因素。适当选择速度、进给速率以及钻头的几何形状可以优化金属切削率和孔的质量[13]。同时，实际孔径可能会随着切削速度和进给率的增大而增大[14]。自准直原理已被应用于测量深孔的圆度、圆柱度和直线度[15]。钻削过程中的动态特性及其对钻削质量的影响也已经被研究[16-18]。

总而言之，由于新的测量方法以及在钻孔过程中的各种力的新模型的采用，使得对于磨损机理及其影响因素的研究取得了很大的进展。但考虑切屑形成，切削参数与加工质量之间的关系等，复杂的磨损机理需要更多的相关研究。本文致力于建立一个钻削的力学模型。

2 力学模型

一般枪钻钻头的结构如图1所示。Z轴沿枪钻轴

线指向钻尖，X轴在前刀面上垂直于轴线指向侧刃方向并通过钻尖，Y轴与X轴、Z轴形成右手坐标系。平面型后刀面枪钻的刃部一般由五个平面组成，分别是：外刃第一后刀面S11、外刃第二后刀面S12、钻尖后刀面S2、内刃后刀面S3和导流面S4。单边切削刃被钻尖A划分为外切削刃（简称外刃）和内切削刃（简称内刃），其中A点为钻尖、O点为几何中心、C点为钻沟底点(图1b)。

来稿日期：2013-09-16

图1指出了枪钻的几何参数：（1）钻尖整体参数：枪钻直径d、钻沟底偏心距e、钻尖偏心距s；（2）外刃后刀面参数：外刃锋角β1、外刃第一后角α11、外刃第二后角α12和外刃第一后刀面宽度w；（3）内刃后刀面参数：内刃锋角β3、内刃后角α3；（4）刀尖后刀面参数：刀尖后角α2；（5）走油面参数：走流面与XOZ面之交线与X轴反方向之夹角β4、走流面控制角κ。为了简化，图1中忽略了冷却孔和导向支撑面的参数。

图1 枪钻钻刃示意图

由于加工过程中枪钻的受力及运动状态十分复杂，为了便于分析，做出如下假设：（1）各个切削力分量和导向支撑面上的摩擦力、正压力等均匀分布，力简化为集中力；（2）由于钻头的轴向尺寸相对于钻杆来说很小，可认为各力均作用在同一个平面上；（3）钻头侧刃上的正压力和摩擦力与其他力相比均很小，或影响甚微，故在分析受力时可忽略不计。

通过以上假设，钻头的受力可以分为三大部分：内外切削刃上的法向力和摩擦力，导向支撑面上的法向力和摩擦力以及间隙面上的冷却液形成的液压力（正压力），如图2所示。

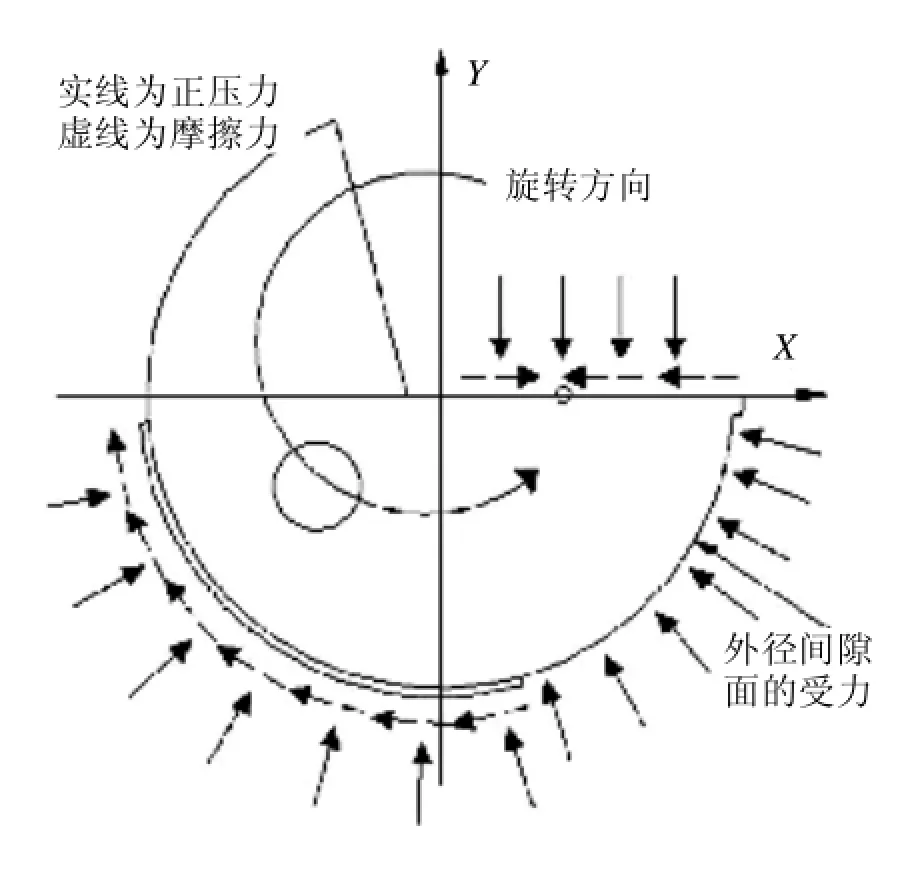
图2 枪钻钻头受力示意图

主切削刃上的力产生于切削刃的切削作用，正压力均匀连续地分布在切削区域，方向垂直于前刀面；切削刃上的摩擦力也是均匀连续分布的，方向垂直于切削刃且平行于前刀面。由于内外切削刃的方向不同，摩擦力在X轴方向的分力方向相反。导向支撑面的正压力与摩擦力都是均匀和连续分布的，正压力是用来平衡切削刃上的力和间隙面上的力，方向垂直于支撑面，指向圆心；周向摩擦力则是阻碍枪钻的旋转，方向沿着支撑面的圆周，与枪钻的旋转方向相反；轴向摩擦力方向沿Z轴方向，与枪钻的进给方向相反。冷却液在间隙面上的法向液压力是均匀连续分布的，方向指向圆心。

2.1 支撑面上的力

将导向支撑面上的均布正压力简化成集中力Rp，周向摩擦力简化成Rfx、Rfy，正压力Rp可以表示为

其中，p为单位正压力，μ为摩擦系数，δ为支撑面在Z轴方向与孔内壁的接触宽度，r为枪钻的半径，ω为角度变量，θ1为支撑面的初始角，θ2为支撑面的终止角。

Rp方向指向圆心，力的作用线指向支撑面中间，角度为(θ1＋θ2)/2，支撑面上单元周向摩擦力可以分解为图3所示。当θ1≤ω≤π/2,dRfx指向-X轴，则Rfx可表示为

图3 导向支撑面上的力的简化

当π/2＜ω≤θ2，dRfx指向-X轴，则Rfx可表示为

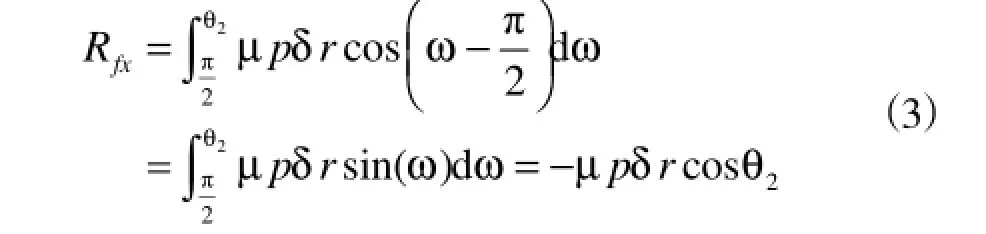
在[θ1，θ2]区间内，Rfx的方向都是指向-X轴，所以Rfx可以简化为

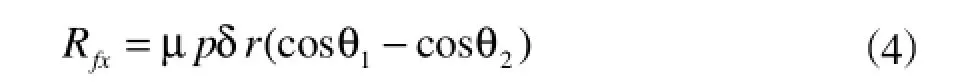
类似地，Rfy指向Y轴，并可表示为

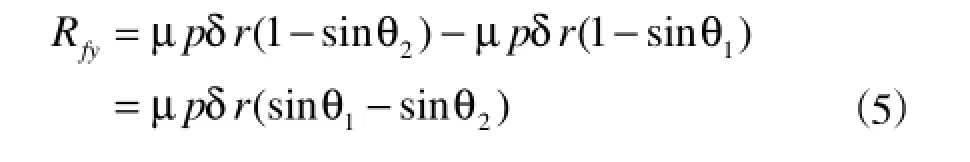
导向支撑面上的周向摩擦力所产生的力矩可以表示为

导向支撑面上的轴向摩擦力可以表示为

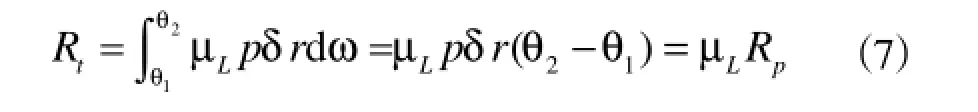
其中，μL为轴向摩擦系数。考虑到硬质合金的硬度较高，塑性变形较小，故选用工程中常用的库仑摩擦系数。

2.2 主切削刃上的力

在钻削过程中，切削刃上每点的切削速度都是变化的，钻削力在切削刃上的分布是不均匀的，因此采用积分的方法建立钻削力模型。将主切削刃划分成许多微小的矩形单元，每个微元上法向力压强和摩擦力压强采用能量模型[19]。其中法向力压强和摩擦力压强的对数公式分别为

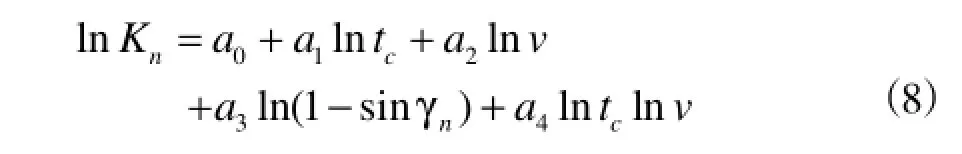
式中，

γn——刀具的法向前角；

v——切削速度；

tc——切削厚度。

单个微元的面积dA可以通过切削厚度乘以微元的切削宽度dx得到，如图4所示。

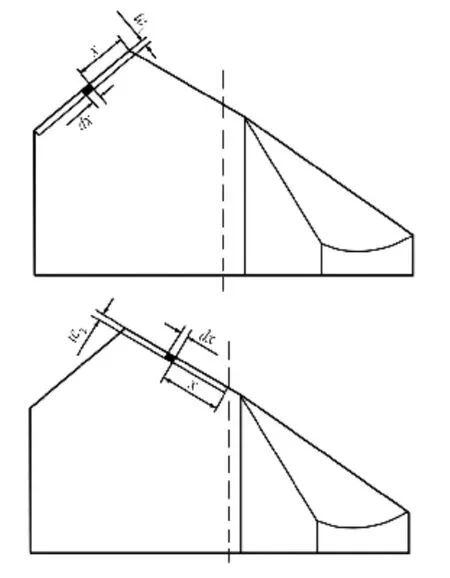
图4 外刃和内刃微元划分图

其中，

β1是外角，β3是内角。所以外刃和内刃微元面积dA可以分别表示为

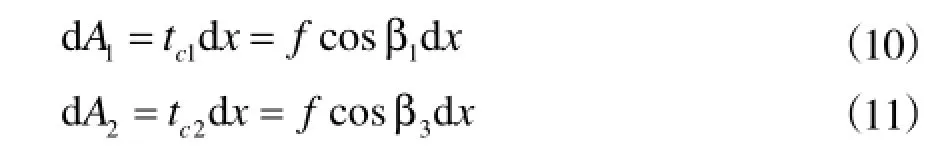
通过积分分别求出外刃和内刃上简化法向力（Fn1，Fn2）和简化摩擦力（Ff1，Ff2），再通过摩擦力（Ff1，Ff2）在 X轴向分解，就可以得到径向摩擦力（Fs1，Fs2），如图5所示。

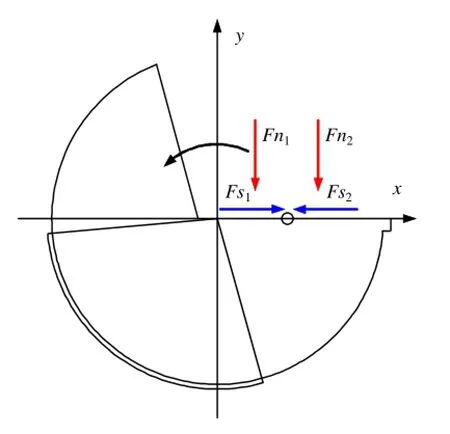
图5 外刃和内刃上受力简化图

所以外刃上的力可以表示为

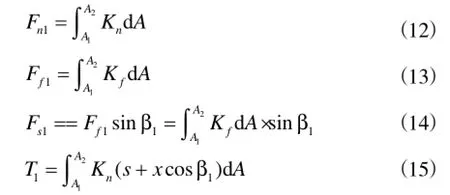
又因为ν=2πn(s+xcosβ1)/60，两边同时微分可得

结合式（8～16），最终表达式如下

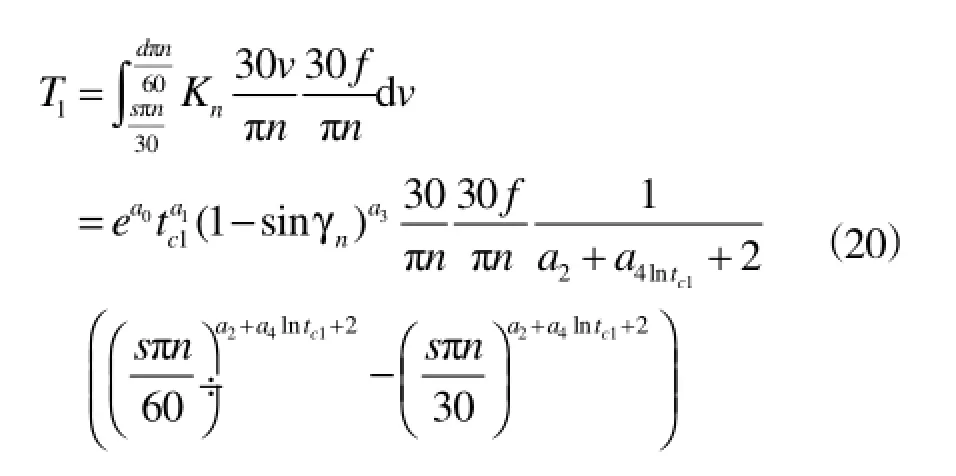
同时，通过式（17）和（20）又可以得出外刃法向力Fn1的力臂

同理，可求得内刃上的力Fn2、Ff2、Fs2，力矩T2以及力臂L2的表达式。

2.3 间隙面上的力

冷却液法向力与冷却液系统有关，因此可以将均匀分布的法向力简化为集中力Rh，力的作用线指向间隙面中间，如图6所示。

图6 冷却液法向力简化

2.4 枪钻力学模型

枪钻钻刃上X-Y平面受力分布图，如图7所示。根据受力分布图，分别列出X、Y方向的力学平衡方程，可得

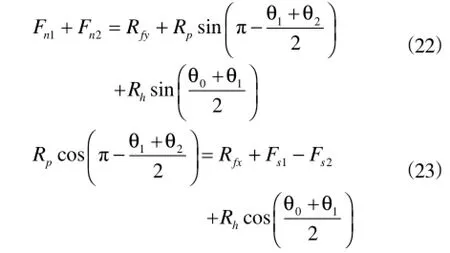
联立式（17）、（19）、（22）、（23）以及Fn2和Fs2的表达式，可以解出Fn1、Fn2、Fs1和Fs2。同时，结合式（4）、（5）、（22）及（23），可以解出Rp。

又因为枪钻的力矩Tt可以表示为

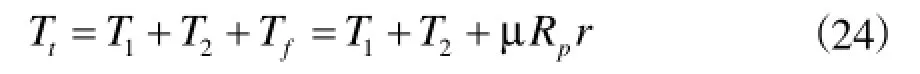
联立式（20）、（24）及T2的表达式，可以解出T1、T2和Tt。

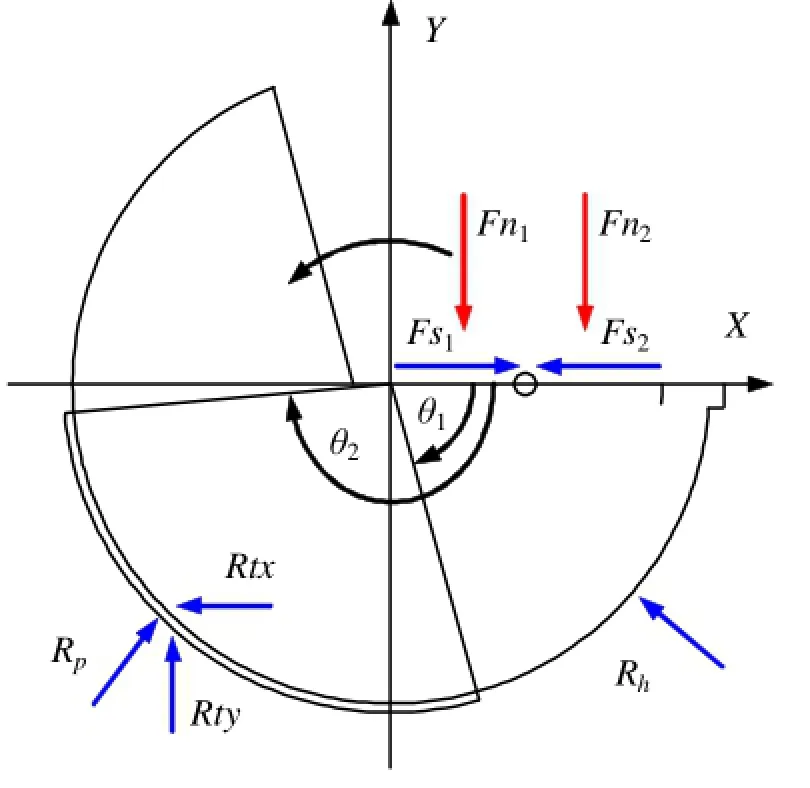
图7 枪钻钻刃X-Y平面受力分布图

枪钻的轴向力Fz可以分成两部分，主切削刃上的轴向摩擦力Ft和导向支撑面上的轴向摩擦力Rt。主切削刃上的轴向摩擦力指向Z方向，它是由外刃和内刃上摩擦力在Z轴方向的合成而来，如图8所示。Ft和Fz表达式分别为

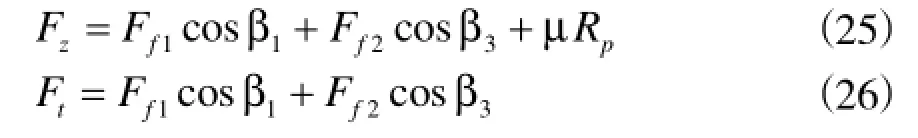
由以上等式可知，枪钻的轴向力和力矩不仅和几何结构参数有关，还与切削参数及工件的材料性能有关。

3 实验与分析

切削实验采用了DECKEL MAHO DMU 50 evo linear五轴加工中心，并采用精度高的液压夹头夹持焊接硬质合金枪钻。表1中列举了枪钻的几何参数。

实验材料为45钢，工件为直径150 mm、厚度51 mm的圆柱形，硬度为200 HV。同时，采用了KISTLER9272四向压电式测力仪、KISTLER5070A电荷放大器以及相应的数据采集与处理系统，在室温为20℃时，测量实验中的切削力（图8）。测力系统坐标系定义：进给方向为X，刀齿切入方向为Y，刀具轴向为Z。

由于枪钻的长径比较大，本实验采用的加工预钻孔方式为：先用一把Φ5钻头钻出深7.5 mm的预钻孔，然后再用枪钻钻至孔深42 mm。根据以往加工经验并结合现有条件，选取了7个不同的主轴转速（1 000～4 000 r/min，间隔500 r/min）、5个进给量（0.02、0.028、0.036、0.044和0.052 mm/r），分别进行单因素试验，共35个方案。

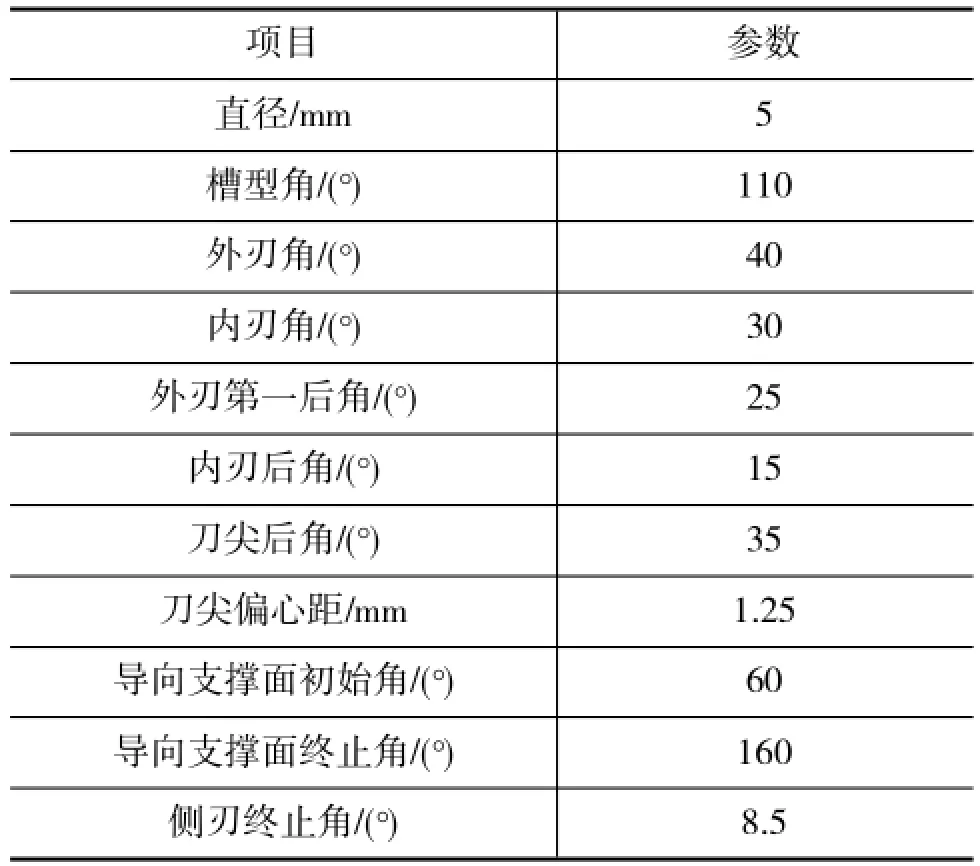
表1 枪钻的几何结构参数

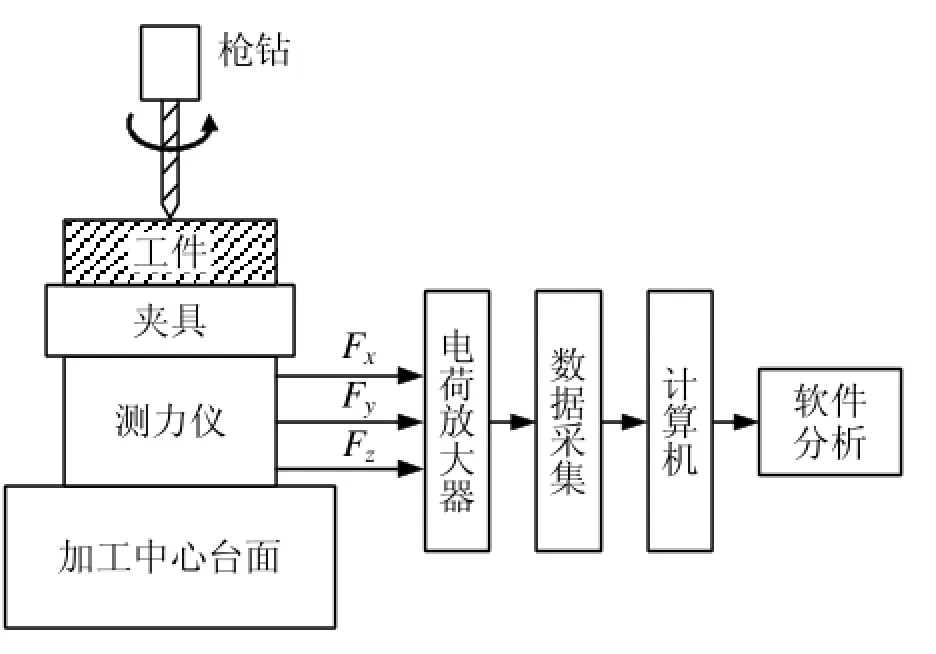
图8 试验系统平台的搭建原理

在单因素试验结束后，以转速n=4 000 r/min，f=0.036 mm/r的参数继续加工，进行枪钻的磨损试验。在实验过程中定义枪钻的寿命标准为：以枪钻后刀面磨损量VB=1.0 mm为标准[20]。本文采用扭矩超过额定扭矩的10%作为标准，一旦扭矩超过允许值就停止试验，即认为达到寿命。试验后利用Zoller对刀仪和超精度三坐标测量机对枪钻的磨损，已加工孔的孔径和圆柱度进行检测分析。同时，采集到的信号由Dynoware（Kistler测力仪软件）进行分析处理，见图9。

由于进给量f增大，切削厚度tc增大，切削面积增大，切削负载增大，故Fz增大。又由于进给量f增加导致切削厚度tc增加，从而引起了前刀面摩擦系数u1的减小，即摩擦角β的减小，所以剪切角φ（φ=π/4-β+γ/2）也变大，切削变形也就变小[21]。前者是直接影响，而后者是间接影响。因此，轴向力Fz是随着进给量f增加而增加，见图10。为使曲

线图清晰可辨认，仅绘制了4根曲线。

图9 采集典型的力学信号

图10 轴向力Fz随进给量f的变化规律

如图11所示，力矩Tt也是随着进给量f增大而增大。力矩Tt分为两部分：切削力矩T与当量摩擦力矩Tf。切削力的增加也会造成支撑面上的正压力RP增大。

轴向力Fz总体是随着切削速度v的增加而减少，见图12。这里将主轴转速n视作切削速度v，是因为它们之间为线性关系。当进给量f越大时，曲线Fz的波动就越小。产生该现象的原因是：当f较低时，随着v的增大，前刀面摩擦系数u1增加，剪切角φ减小，轴向力Fz增大。然而，当f较高时，结果相反。当f继续增加时，u1的影响变得很小。因此，曲线Fz的波动就变小。如图13所示，当f相同时，随着v的增加，Tt会减小；当v相同时，随着f的增加，Tt会增大。

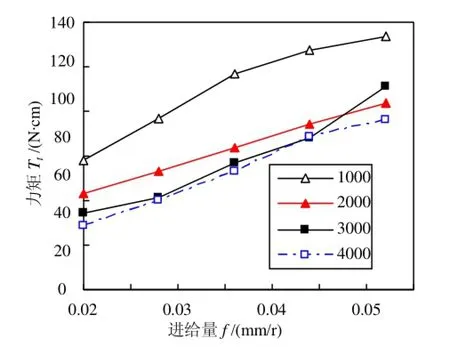
图11 力矩Tt随进给量f的变化规律

图12 轴向力Fz随切削速度v的变化规律

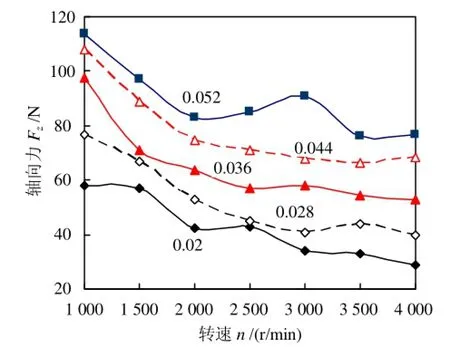
图13 力矩Tt随切削速度v的变化规律

轴向力Fz和力矩Tt的实验值和理论计算值的比较，如图14和图15所示。当3 000＜n＜4 000 r/min，f=0.052 mm/r时，轴向力Fz的计算值与试验值的偏差最大达到22.5%。除此之外，轴向力Fz的计算值与试验值的偏差小于13%。这是因为u1和v不是线性关系。另一个原因是工件材料的不均匀以及在高切削速度时忽略了u1的作用。例如，当材料中有硬质点时，在n=3 000 r/min，f=0.052 mm/r的条件下，Tt最大偏差在16%，且Fz最大偏差在22.5%。

4 结论

本文基于一些合理的假设，通过积分的方法对主切削刃、导向支撑面、间隙面上的受力进行分析

简化，借鉴麻花钻的能量模型建立了硬质合金枪钻的力学模型。通过钻削45钢工件的实验后发现，随着进给量的增加以及切削速度的降低，枪钻轴向力和力矩会增大。

图14 切削45钢的轴向力计算值与实测值对比

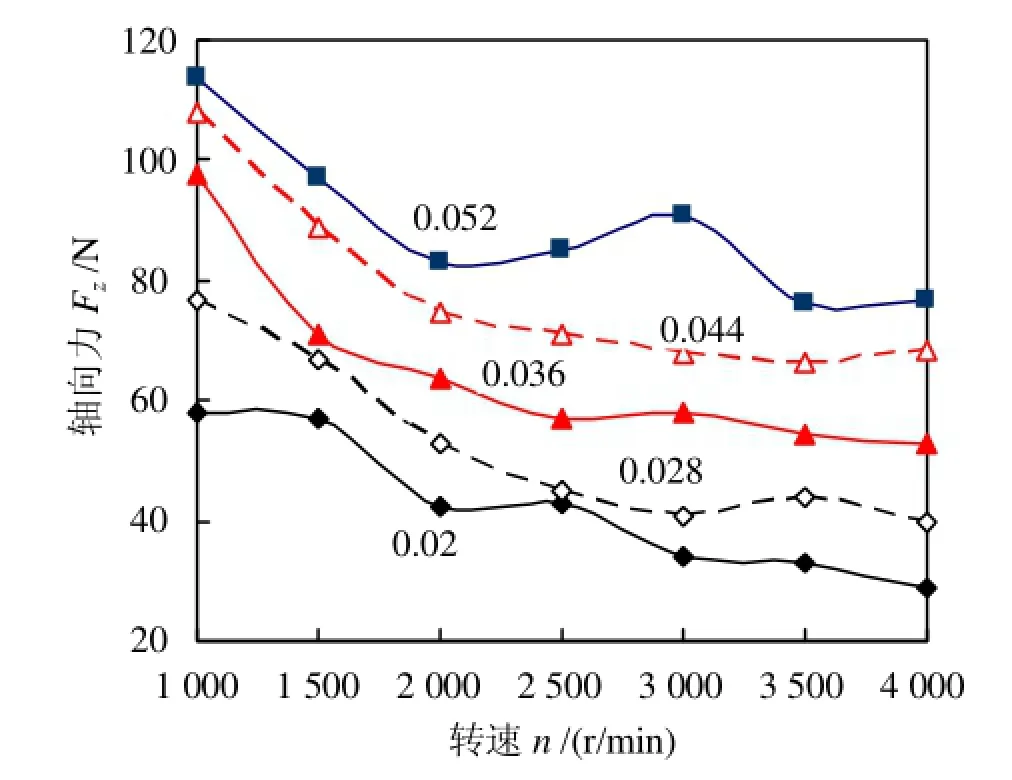
图15 切削45钢的力矩计算值与实测值对比

1 Jung J H,Ni J.Prediction of Coolant Pressure and Volume Flow Rate in the Gundrilling Process[J]. Journal of Manufacturing Science and Engineering, 2003,125(4):696-702.

2 Gill S S,Singh J,Singh H,et al.Investigation on Wear Behaviour of Cryogenically Treated TiAlN Coated Tungsten Carbide Inserts in Turning[J]. International Journal of Machine Tools&Manufacture, 2010,51(1):25-33.

3 Strenkowski J S,Hsieh C C,Shih A J.An Analytical Finite Element Technique for Predicting Thrust Force and Torque in Drilling[J].International Journal of Machine Tools&Manufacture,2004 44(12-13):1413-1421.

4 Griffiths B J.Modeling Complex Force Systems, Part 1:the Cutting and Pad Forces in Deep Drilling[J]. ASME Journal of Engineering for Industry,1993, 115(2):169-176.

5 Jung J H,Ke F.A Gundrilling Force System[J]. International Journal of Machine Tools&Manufacture, 2007,47(7-8):1276-1284.

6 Aykut S,Bagci E,Kentli A,et al.Experimental Observation of Tool Wear,Cutting Forces and Chip Morphology in Face Milling of Cobalt Based Super-Alloy with Physical Vapour Deposition Coated and Uncoated Tool[J].Materials&Design,2007, 28(6):1880-1888.

7 Obikawa T,Usui E.Computational machining of Titanium Alloy-Finite Element Modeling and a Few Results[J].ASME Journal of Manufacturing Science and Engineering,1996,118(2):208-215.

8 Obikawa T,Usui E,Sasahara H,et al.Application of Computational Machining Method to Discontinuous Chip Formation[J].ASME Journal of Manufacturing Science and Engineering,1997,119(4B):667-674.

9 El Hossainy T M,El-Shazly M H,Abd-Rabou M. Finite Element Simulation of Metal Cutting Considering Chip Behavior and Temperature Distribution[J].Materials and Manufacturing Processes,2001,16(6):803-814.

10 Warnecke G,Oh J D.A New Thermo-Viscoplastic Material Model for Finite-Element-Analysis of the Chip Formation Process[J].CIRP Annals-Manufacturing Technology,2002,51(1):79-82.

12 Li K,Gao X L,Sutherland J W.Finite Element Simulation of the Orthogonal Metal Cutting Process for Qualitative Understanding of the Effects of Crater Wear on the Chip Formation Process[J].Journal of Materials Processing Technology,2002,127(3):309-324.

13 Syed I,Bahr B,Sha J,et al.Experimental Study of Hole Quality in Drilling of Titanium Alloy(6AL-4V) [C].SAE 2002-01-1517.

14 Furness R J,Wu C L,Ulsoy A G,Statistical Analysis

of the Effects of Feed,Speed,and Wear on Hole Quality in Drilling[J].ASME Journal of Manufacturing Science and Engineering,1996, 118(3):367-375.

15 Hiroshi M,Akio K,Hiromichi O,et al.Development of a Deep-Hole Measuring System by Using Autocollimation Principle(3rd Report): Measurement of Roundness,Cylindricity and Straightness[J].Journal of the Japan Society for Precision Engineering,2008,74(11):1220-1224.

16 Ma L J,Wang X B,Liu G J,et al.Study on Torsional Vibration Performance of Twist Drill in Axial Vibration Drilling[C].International Conference on Measuring Technology and Mechatronics Automation, 2009,Volume 1:732-737.

17 Teckinalp O,Ulsoy A G.Effects of Geometric and Process Parameters on Drill Transverse Vibrations[J]. ASME Journal of Engineering for Industry,1990, 112(2):189-194.

18 Altintas Y,Weck M.Chatter Stability of Metal Cutting and Grinding[J].CIRP Annals-Manufacturing Technology,2004,53(2):619-642.

19 Watson A R.Drilling Model for Cutting Lip and Chisel Edge and Comparison of Experimental and Predicted Results I-Initial Cutting lip Model[J]. International Journal of Machine Tool Design and Research,1985,25(4):347-365.

20 Heinemann R K,Hinduja S,Investigating the Feasibility of DLC-Coated Twist Drills in Deep-Hole Drilling[J].The International Journal of Advanced Manufacturing Technology,2009,44(9-10): 862-869.

21 Ke F,Ni J,Stephenson D A.Chip Thickening in Deep-Hole Drilling[J].International Journal of Machine Tools and Manufacture,2006,46(12-13): 1500-1507.

图7 不同零气压扭矩下柴油机加速性能

图8 不同零气压扭矩下柴油机加速时间与自由加速烟度关系曲线

6 结束语

试验结果表明，降低飞轮转动惯量、合理匹配增压器、提高低速零气压扭矩等有利于提升柴油机的加速性。但采取这些措施改善柴油机加速性的同时，分别会有噪声振动增大、作业油耗上升、自由加速烟度变差等缺陷。

参考文献

1黎苏，黎晓鹰，黎志勤．汽车发动机动态过程及其控制[M]．北京：人民交通出版社，2000．

2周红秀，姚春德．改善车用增压发动机加速性的技术发展[J]．柴油机设计与制造，2008（2）．

3 Ledger J D,Benson R S,Furukawa H．Improvement in Transient Performance of a Turbocharged Diesel Engine by Air Injection into the Compressor[C]．SAE 730665．

4 Harndorf H．向涡轮增压器补充喷气以改善增压柴油机的瞬态响应．国外内燃机[J]．1996（2）．

5陈怡，黄佑生．利用空气引射方案改善涡轮发动机的加速性的研究[C]．大功率柴油机学术年会论文，1983．

6李呈剑，凌建群，汤静．装载机载荷谱分析与应用[J]．柴油机设计与制造，2009（4）．

The Force System of the Welding Carbide Gun Drill to Cut 45 Steel

Jia Wenxing
（School of Mechatronics Engineering and Automation,Shanghai University,Shanghai 200072,China）

This paper focused on the force system of the welding carbide gun drill to cut 45 steel.A carbide gun drill force system had been established by the integration of forces on the main cutting edge, wear pad and outer diameter(OD)relief,and the mechanical equilibrium equations,applying specific energy model and considering the geometry parameters,machining parameters and material properties.The cutting experiment data revealed that the force and torque increased with the cutting feed ascending and the cutting speed descending.

welding carbide gun drill,force system,cutting experiment

贾文幸（1989-），男，硕士研究生，主要研究方向为制造工艺与刀具。

10.3969/j.issn.1671-0614.2013.04.009