m阶非齐次马氏链关于广义赌博系统的一类强极限定理

王康康，宗德才，孟义平

(1.江苏科技大学数理学院，江苏镇江212003)(2.常熟理工学院 计算机科学与工程学院，江苏常熟215500)(3.上海交通大学数学系，上海200240)

设{Xn，n≥0}为定义在概率空间(Ω，F，P)上并于S={1，2，…，N}上取值的任意随机变量序列，其联合分布为

如果{Xn，n≥0}为m阶非齐次马氏链，其m维初始分布与m阶转移概率分别为

则有

马氏链的极限理论是马尔可夫过程研究的基本领域之一.众所周知，对齐次马氏链的极限定理已经有相当完善的结果.近几十年来，广大学者对非齐次马氏链的极限理论和遍历性展开了大量研究，取得了深入的结果.如文献［1］中讨论了可列非齐次马氏链相对频率的两个不等式;文献［2］中讨论了可列非齐次马氏链泛函的一类强极限定理;文献［3-4］中研究了非齐次马氏链的渐近均匀分割性及Shannon-Mcmillan定理;文献［5］中研究了非齐次马氏链随机转移概率的强极限定理;最近，文献［6］中也对非齐次马氏链随机和的强偏差定理作了一些研究.

高阶马尔可夫链是一般马尔可夫链概念的自然推广，随着马氏链理论的不断发展和应用，人们对高阶马尔可夫链的理论和应用也越来越有兴趣，如信息论中关于Shannon-McMillan定理的研究便是其核心问题之一.而高阶马尔可夫链也是一类非常重要的信源，如语声，电视信号等往往都是高阶马尔可夫信源.因此，研究高阶马尔可夫链的强极限理论具有非常广泛的理论和实际意义.文献［7］中首先研究了二重非齐次马氏链泛函关于可预报序列的若干极限定理及AEP性质;文献［8］中讨论了m阶非齐次马氏链的一些Shannon-Mcmillan定理;其后，文献［9］又对m阶非齐次马氏链的一类Shannon-Mcmillan随机偏差定理做了进一步讨论.

文中采用条件矩母函数与构造非负鞅相结合的方法，研究m阶非齐次马氏链多元函数关于广义赌博系统的一类强极限定理.通过允许选择函数在任意区间中取值，推广了随机选择的概念.作为推论得到了一般情况下m阶非齐次马氏链多元函数的强极限定理以及m元状态序组关于广义随机赌博系统的一类强极限定理.

定义 给出广义随机选择的概念，即对于一组定义在 Sn(n=1，2，…)上并取值于任意区间［a，b］(a，b∈R)的非负实值函数列 fn(x0，…，xn).令

那么 fn(x0，…，xn)称为选择函数，{Yn，n≥0}称为广义赌博系统或广义随机选择系统(传统的随机选择系统取值于两点集{0，1}).

1 主要结果

定理1 设{Xn，n≥0}为具有m维初始分布(2)与m阶转移概率(3)的m阶非齐次马氏链.{Yn，n≥0}如前定义.g(x0，…，xm)为定义在 Sm+1上的任意实值函数.如果选择函数fn(n≥m)均在任意有限区间［a，b］中取值，

则有

证明:考虑概率空间(Ω，F，P)，设s＞0为常数.令

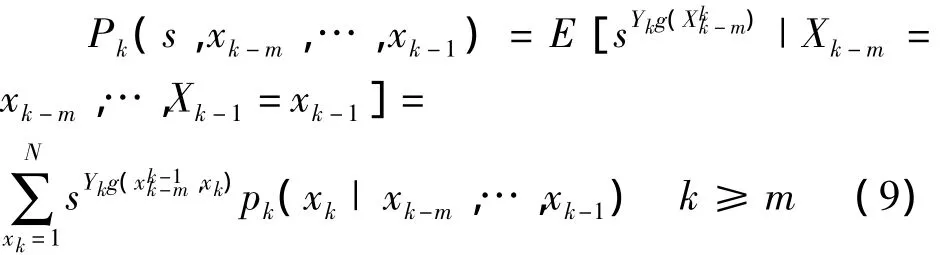
Pk(s，xk-m，…，xk-1)称为在条件 Xk-m=xk-m，…，Xk-1=xk-1下 Ykg(Xk-m，…，Xk)的条件矩母函数.

令

由式(9～11)可知

则 q(s，x0，…，xn)，n=1，2，…是 Sn上的一组相容分布.令

由于{Tn(s，ω)，n≥1}是 a.s.收敛的非负上鞅，故由 Doob鞅收敛定理［10］有

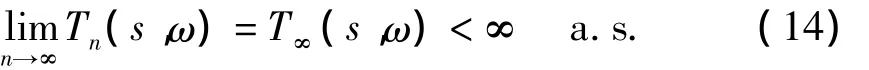
因而由式(7)有

由式(4，10～11，13)有

由式(15，16)有

根据上极限的性质

并注意到 G=max{|a|，|b|}，存在，且|Yk|≤G，M=max{g(x0…xm)，x0…xm∈S}，由式(17)有

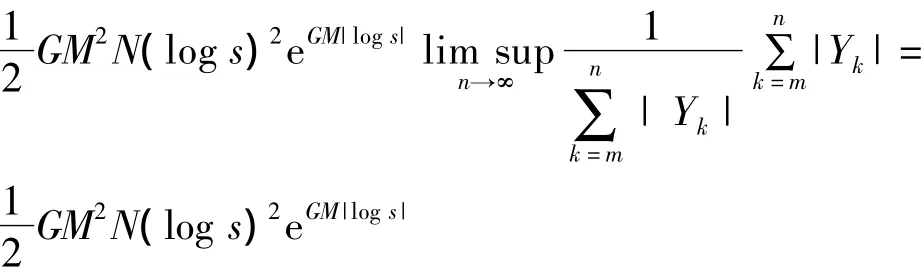
a.s.ω∈D (20)

设s＞1，由式(20)有

取si＞1，i=1，2，…，使si→1(i→∞ 时)，则对所有的i，由式(21)有

设0＜s＜1，由式(20)有

取0 ＜si＜1，i=1，2，…，使si→1(i→∞时)，那么对所有 i，由式(23)有

于是由式(22，24)有

即证式(8)成立.

推论1 设{Xn，n≥0}为具有m维初始分布(2)与m阶转移概率(3)的m阶非齐次马氏链.g(x0，…，xm)如定理1中所定义.则有

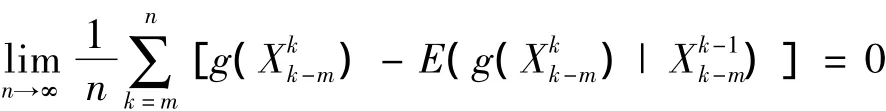
证明:在定理1中令 fn≡1，则 Yn≡1，.即有 D=Ω.

于是由式(8)即可得式(26).

2 m元序组关于赌博系统的若干强极限定理

设σn(i0，…，im)表示被选择函数 Yk(m≤k≤n)选出的m+1元序组的序列(X0，…，Xm)，(X1，…，Xm+1)，…，(Xn-m，…，Xn)中 (i0，…，im)出现的次数.即

式中:

则有如下结论:

定理2 设{Xn，n≥0}为具有m维初始分布(2)与m阶转移概率(3)的非齐次m阶马氏链.σn(i0，…，im)，{Yn，n≥0}如前定义.则有证明:在定理 1 中令 g(Xk-m，…，Xk)=

δi0…im(Xk-m，…，Xk)，注意到

n

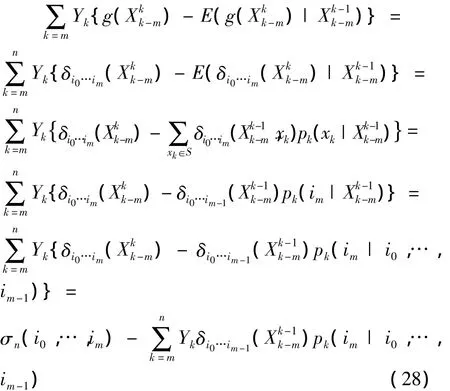
于是由式(28，8)即可得(27)成立.

推论2设{Xn，n≥0}为具有m维初始分布(2)与m阶转移概率(3)的m阶非齐次马氏链.设Sn(i0，…，im)表示(i0，…，im)在 m+1 元序组(X0，…，Xm)，(X1，…，Xm+1)，…，(Xn-m，…，Xn)中出现的次数.即

则有

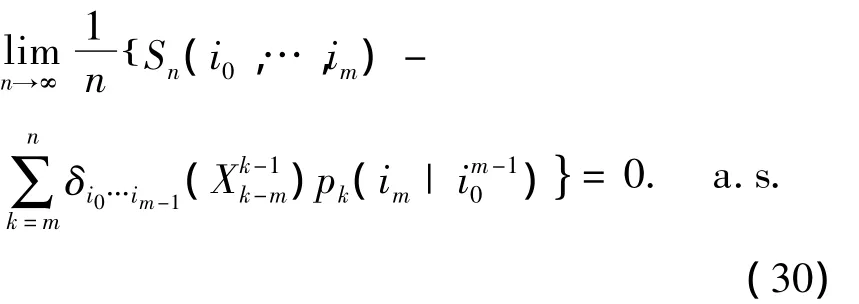
证明:在定理2 中令Yn≡1，即有 σn(i0，…，im)=Sn(i0，…，im)，D=Ω.由式(27)便可得式(30)成立.

定理3 设{Xn，n≥0}为具有m维初始分布(2)与m阶转移概率(3)的m阶非齐次马氏链.{Yn，n≥1}如上定义.记 σn(im)为随机选择系统Yk(0≤k≤n)选出的随机序列(X0，…，Xn)中状态im出现的次数.即).则有

证明:在定理 1 中令 g(Xk-m，…，Xk)=δim(Xk)，注意到

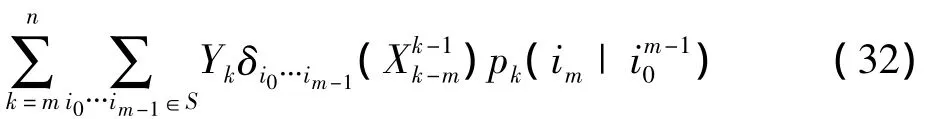
于是由式(8，32)可得式(31)成立.

推论3 设{Xn，n≥0}如定理2所定义.记Sn(im)为状态im在随机序列(X0，…，Xn)中出现的次数.即.则有

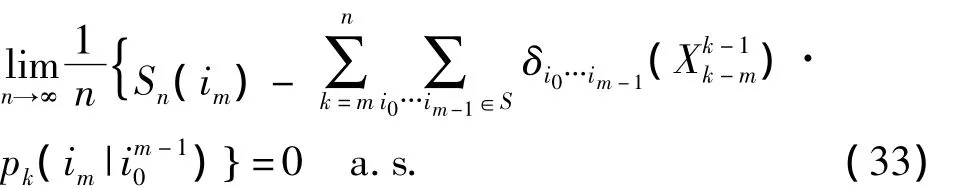
证明:在定理3中令 Yn≡1，n≥0.即有σn(im)=Sn(im)，D=Ω.于是由式(31)即可得式(33)成立.

References)

［1］Liu Wen.A strong limit theorem for arbitrary countable nonhomogeneous Markov chains［J］.Chinese J Math，1996，24(3):211 -232.

［2］Liu Wen，Liu Guoxin.A class of strong laws for for functions of countable nonhomogeneous Markov chains［J］.Stat Probab Letts，1995(22):87 -96.

［3］刘文，杨卫国.关于非齐次马氏信源的渐近均分割性［J］.应用概率统计，1997，13(4):359 -366.Liu Wen，Yang Weiguo.The asymptotic equipartition property for the nonhomogeneous Markov chain［J］.Chinese Journal of Probability and Statistics，1997，13(4):359 -366.(in Chinese)

［4］Liu Wen，Yang Weiguo.An extension of Shannon - Mcmillan theorem and some limit properties for nonhomogeneous Markov chains［J］.Stochastic Process Appl，1996，61:129-145

［5］Liu Wen.A strong limit theorem for the harmonic mean of the random transition probabilities of finite nonhomogeneous Markov chains［J］.Acta Math Sci，2000，20(1):81-84.

［6］Wang Kangkang，Chen Qing.A class of random approximation theorems for random sums of arbitrary stochastic sequence on nonhomogeneous Markov chains［J］.Journal of Mathematical Research and Exposition，2009，29(6):1022-1028.

［7］Wang Zhongzhi，Yang Weiguo.Some strong limit theorems for both nonhomogeneous Markov chains of order two and their random transforms［J］.J Sys Sci ＆ Math Scis，2004，24(4):451 -462.

［8］王康康，李芳.m阶非齐次马氏信源的一类Shannon-Mcmillan定理［J］.江苏科技大学学报:自然科学版，2009，23(2):176-178.Wang Kangkang，Li Fang.A class of Shannon-Mcmillan theormes for mth-order nonhomogeneous Markov information source［J］.Journal of Jiangsu University of Science and Technology:Natural Science Edition，2009，23(2)176 -178.(in Chinese)

［9］ Wang Kangkang.Some research on Shannon-McMillan theorem for mth-order nonhomogeneous Markov information source［J］.Stochastic Analysis and Applications，2009，27(6):1117 -1128.

［10］Chung K L.A course in probability theory［M］.2nd.New York:Academic Press，1974:354.