一种复杂多边形区域上重积分的计算方法

李京梁，施国华

(江苏科技大学张家港校区基础部，江苏张家港215600)

关于重积分的计算方法一直是高等数学和数学分析［1-2］中的重要内容.由于积分区域的复杂性，重积分的计算可能变得十分困难甚至不可能，因此，简化积分区域在重积分运算中十分重要.文中首先给出平面上任意四边形和三角形区域到对称正方形区域R=［-1，1］×［-1，1］的区域变换，由此简化积分区域，然后结合区域分裂的思想，提出一种新的解决复杂多边形区域上二重积分的方法.

1 两个区域变换

1)XOY平面上的任意三角形区域ABC到ROS平面上正方形区域 R=［-1，1］×［-1，1］的映射［5-7］(图 1 左)为

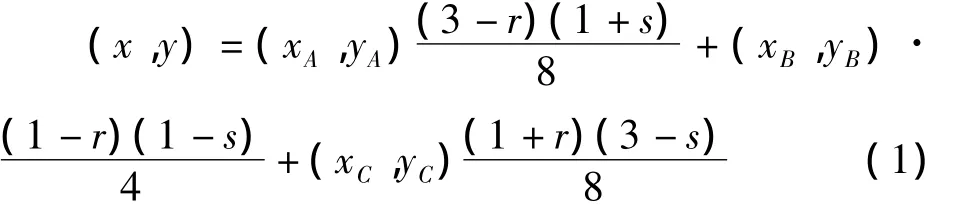
此映射将边AC的中点映射到区域R的顶点d.

2)XOY平面上的任意四边形ABCD到ROS平面上正方形 R=［-1，1］×［-1，1］的映射［3-4］(图1右)为

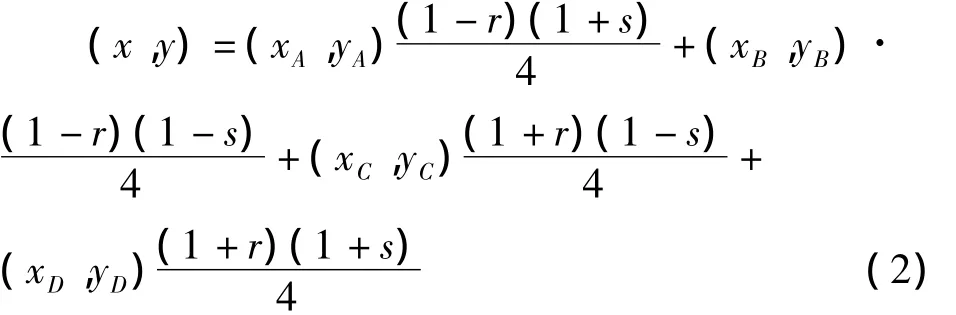
图1 两种区域变换Fig.1 Two transformations of domain

2 区域分裂及化简二重积分

对于XOY平面上的任意一个复杂多边形区域D，可以将其分裂成四边形区域和三角形区域的组合，如下图所示，D=D1+D2+D3+D4.

图2 区域D的分裂Fig.2 Division of domain

利用映射(1，2)，结合重积分关于积分区域的可加性，那么在区域D上的二重积分

式中:R 是正方形区域［-1，1］×［-1，1］;g1(r，s)和 g4(r，s)是将映射(2)代入 f(x，y)后的函数，J1是映射(2)的雅可比行列式;g2(r，s)和g3(r，s)是将映射(1)代入 f(x，y)后的函数，J2是映射(1)的雅可比行列式;这样在区域D上的二重积分∬Df(x，y)dxdy就化成了一个在正方形区域R上的二重积分，对于某些二重积分，结合函数的奇偶性质，可以大大简化积分的计算，下面的例子给出说明.

3 两个例子

例1:设积分区域E如图3所示，各点坐标为:A(0，2)，B(-1，0)，C(1，-1)，D(3，2)，被积函数取为3x-2y，则由映射(2)运算知:

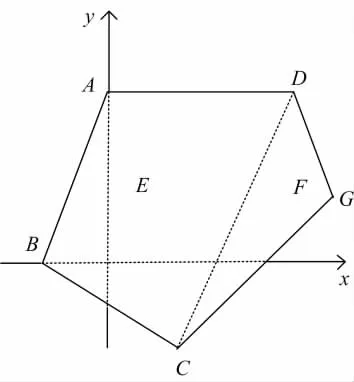
图3 复杂多边形Fig.3 Complex polygon

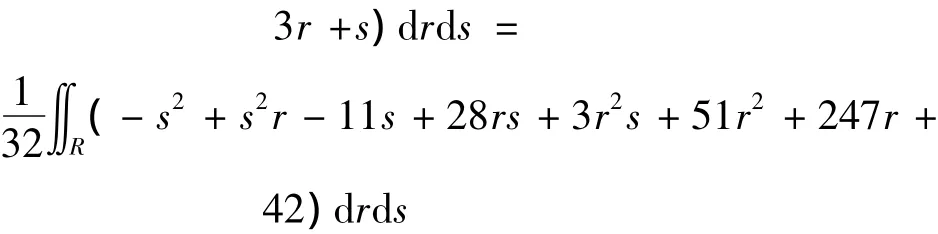
例2:设积分区域E∪F如图3所示，G点坐标为(4，1)，被积函数仍取为 3x-2y，则由映射(1)运算知:

(3x-2y)|=(55-5s+15r-5rs)/8，J1=(10-5r-5s)/16

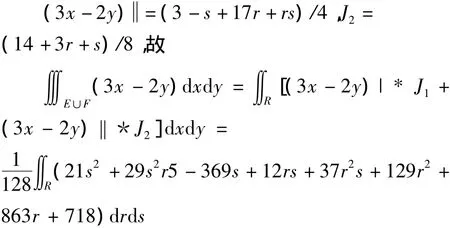
References)

［1］伍胜健.数学分析［M］.北京:北京大学出版社，2010:131-163.

［2］同济大学数学系.高等数学［M］.北京:高等教育出版社，2007:132-153.

［3］胡健伟，汤怀民.微分方程数值方法［M］.北京:科学出版社，2007:324-328.

［4］Canuto C，Hussaini M Y，Quarteroni A，et al.Spectral Methods［M］.Berlin:Springer，2006:98 -115.

［5］张帅胤，马和平，王立联.椭圆型方程的Legendre三角单元谱元法［J］.上海大学学报:自然科学版，2012，18(3)，256 -260.Zhang shuaiyin，Ma Heping，Wang Lilian.Legendre triangle spectral element method for the elliptic equation［J］.Journal of Shanghai University:Natural Science，2012，18(3):256 -260.(in Chinese)

［6］Li Y Y，Wang L L，Li H Y，et al.A new spectral method on triangles［C］∥ ICOSAHOM ′09 Conference.Trondheim，Norway:［s.n.］，2009:237 -246.

［7］Canuto C，Hussaini M Y，Quarteroni A，et al.Spectral methods［M］.Berlin:Springer，2006:98 -115.