基于混合蚁群算法的物流配送路径优化研究

王慕抽 （温州大学，浙江 温州 325035）

中国2001年4月颁布的《物流术语》国家标准定义：物流是“物品从供应地向接收地的实体流动过程。根据实际需要，将运输、存储、搬运、包装、流通加工、配送、信息处理等基本功能实施有机结合”。配送是现代化物流系统的重要环节，配送路径选择是物流配送中最关键的问题，它的合理与否关乎配送速度、服务质量、配送成本等。

美国J.Holland教授及团队在1970年代建立发展了遗传算法，它是通过潜在解种群进行搜索，采用概率转移来选择个体，创造新后代，适合数值求解有些带有多数、多变量的NP难题，但过早收敛和搜索效率低等问题。根据蚁群觅食的群体行为，意大利学者Dorigo M等于1991年在法国巴黎召开的第一届欧洲人工生命会议上最早提出了蚁群算法的基本模型；1992年Dorigo M在其博士学位论文中进一步阐述了蚁群算法的核心思想。由于具有较强的群体搜索能力，蚁群算法被运用于求解各种组合优化问题。但研究结果表明在计算过程中有时会陷入局部最小，使整个系统呈现出早熟现象。于是我们构造了遗传算法和蚁群算法相结合的混合蚁群算法为求解物流配送路径优化问题提供了有效的工具。

1 蚁群算法原理和模型

1.1 蚁群算法原理

蚂蚁寻觅食物的过程中，从蚂蚁巢窝启程寻觅食物源，刚开始的时候其路径选择是随机的，但后来路径选择会随着寻觅食物过程的继续而适应性地搜索新的路径。原因主要是蚂蚁在运动过程中，在途径的路径上释放信息素的物质，路径上的信息量随着时间流逝而逐渐消减，信息素物质与路径长度有关，路径越短分泌的信息素越大；如若某一条路径上经过蚂蚁越多，其留下的信息素浓度越强，信息素浓度越强就会吸引更多的蚂蚁从此路径过，这样形成正反馈效应。如此蚂蚁在寻觅食物的过程中就形成一个较优的寻觅食物路径。受蚂蚁寻觅食物路径发现行为的启发，1992年Marco Dorigo在其博士论文中阐述了蚁群算法，并且对其数学模型做了分析、解释。

1.2 蚁群算法模型

2 物流配送路径优化问题的数学模型

各个顾客点需求量和位置及各车辆的装载量已知，按要求用多个车辆对多个顾客需求进行配给货物，寻求好的配送方案，使得总代价最小即我们说的物流配送路径优化。它需要满足：物流配送中心车型、位置唯一且已经；每辆车出发点和任务终止点都是配送中心；每条配送路径上各需求点的总需求量不得超过该车辆的载重量；每条配送路径的长度不得超过配送车辆一次配送的最大行驶距离；每个需求点需求被满足且只能由一辆车送货。

假设有n个客户需配送中心送货，每个客户需求货物量是gi，每辆车载重量为q，数学模型为：

上述模型，m代表所需车辆数；Cij为从点i到点j的运输成本，它包括距离、时间、费用等，可以根据情况，并同时考虑车辆数及运行费用，式（1）是目标函数；式（2）是汽车容量约束；式（3）确保每客户的运输任务由仅有一辆车完成；式（4）和式（5）为到达和离开某一客户的车仅为一辆。

3 物流配送路径优化问题的混合蚁群算法

混合蚁群算法主要思想是将蚁群算法和遗传算法结合起来。因为蚁群算法和遗传算法具有很多类似的特性，蚁群算法和遗传算法都是模拟生物进化的方法，蚁群算法是利用群体智能来搜寻最优解，而遗传算法是利用种群进化来搜寻最优解。蚁群算法具有正反馈和建设性的“贪婪”启发式特性，而遗传算法具有全局收敛性。

物流配送路径中选择混合蚁群算法，省去了蚁群算法一开始寻找最优解的过程，而且遗传算法寻找较优解的速度快，这两种算法的融合，在时间效率上得到了提高。

（1） 初始化参数t=0、NC=0、WK=0、m、q等

fori=1tocustomsdo//customs为客户数量

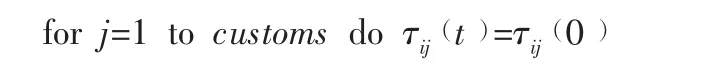
（2） fork=1tomdo//m为蚂蚁的数量

{if满足约束条件

选择下一个客户；更新tabuk表和车辆载重量。

else返回配送中心。}

fork=1tomdo

计算lengthk；

//lengthk为第k只蚂蚁的寻优路径长度

寻找阶段最优解。

（3）对阶段最优解实施变异操作

用线路改进算法优化阶段最优解的子路径；

评价并更新阶段最优解。

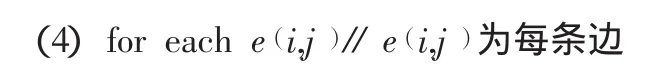
do {更新路径上信息素}；

对τij设置相对应的上界及下界。

（5） NC=NC+1

动态调整信息素的挥发因子ρ；

评价并更新当前最优解。

（6） if NC＞nc

算法结束，输出最优路径及路径长度；

否则转Step2。

4 实例仿真

根据物流配送路径优化问题的混合蚁群算法，本人利用Matlab2012进行编程，计算实例结果进行分析比较。

实例：某配送中心有载容量8t的2辆配送车，各客户的需求量为（单位为t），各客户与配送中心距离如表1所示：

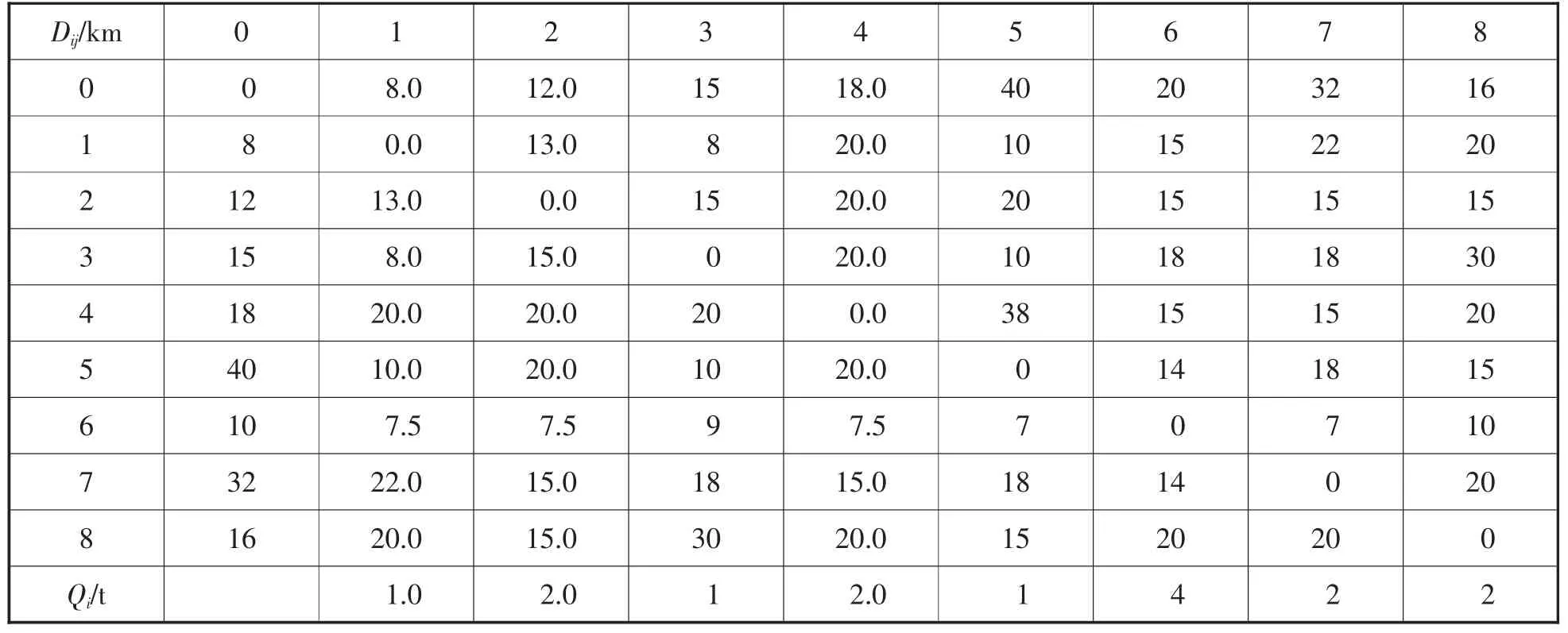
表1 距离与需求量表

运用本文提供的混合蚁群算法对其问题求解，参数设置α＝2，β＝4，ρ＝0.85。利用编程工具Matlab2012获得的物流路径为：0→4→7→6→0,0→1→3→5→8→2→0，随机求解8次，得到结果如表2所示。

表2 混合蚁群算法的计算结果

利用蚁群算法得运输总距离为159km，线路为0→6→5→7→3→0，0→4→8→2→1→0；遗传算法可得总运输距离143km；然而从表2可得其运输总距离为135km，可见利用混合蚁群算法求得的距离较优，此方案满足所规定的约束条件，是所陈述的车辆路径问题的可行解。

5 结束语

本文用混合蚁群算法完成了物流配送车辆路径问题方面的求解。本课题的研究对物流配送路径具有优化作用，节约物流运送成本，提升企业竞争力。从仿真实例来看，该算法的优化质量和效率都优于遗传算法和蚁群算法，增强寻优能力，提高了运算速度，避免算法造成停滞现象，具有较好搜寻全局最优解的能力。

[1] 郎茂祥.用单亲遗传算法求解配送车辆调度问题的研究[J].交通与计算机，2006(1):119-121.

[2] 于文莉.基于混合蚁群算法的物流配送路径优化问题的研究[J].商场现代化，2007(10):137-138.

[3] 陈卫东，王佳.基于混合蚁群算法的物流配送路径优化[J].计算机工程与设计，2009(14):3383-3385.

[4] 李卓君.混合蚁群算法求解物流配送路径问题[J].武汉理工大学学报（交通科学与工程版），2006(2):306-309.

[5] 雷德明，吴智铭.基于粒子群优化的多目标作业车间调度[J].上海交通大学学报，2007,41(11):1796-1800.

[6] 张潇，王江晴.混合蚁群算法在车辆路径问题中的应用[J].计算机工程，2011(12):190-192.

[7] Colorni A.,Dorigo M.,Maniezzo V.,et al.Distributed optimization by ant colonies[C]//Proceedings of the 1st European Conference on Artificial Life,Paris,1991:134-142.

[8] Dorigo M..Optimization learning and natural algorithms[D].Department of Electronics,Politecnico Dimilano,Italy,1992.