养老服务中配送车辆路径问题研究

王鸿雁， 谢 勇 （华中科技大学，湖北 武汉 430074）

现今，中国社会老龄化现象变得日益严重，党中央以及各级政府都越来越重视民生服务中的养老工作，并已将其纳入了政策规划之中。居家养老作为养老服务模式中最符合中国国情的一种模式，正受到社会和群众的大力支持与推广。养老服务中上门服务的配送问题也得到了更广泛的关注。

养老配送服务主要是物资的调度和人员的指派，涉及到顶点、路网对称性、车场点、车型与车程等元素，这构成了车辆路径问题的元素。但是养老服务的主要对象老人的特点是有时候比较多疑挑剔，喜欢讨价还价，所以对蔬菜和牛奶等的新鲜程度以及某些暂时性短缺的药品的即时性比较高，而此类物品自身对时间的要求也比较严格。同时，老人的出行时间、实际的道路交通状况、车辆行驶速度和配送途中各种意外情况等都是不确定因素，因此，配送过程有时间窗约束。另外，车辆本身对载容量和载重量都有一定的限制。可见，养老服务配送问题实际上就是带时间窗的车辆路径问题。

从车辆路径问题提出至今，国内外学者针对车辆路径问题中配载与配送问题已经有过不少研究。杨锦冬[1]基于客户时间窗约束、道路交通条件约束和车辆承载能力约束等限制条件，建立了车辆总行走时间最短和配载货物最多的两目标优化模型组，反映实际的调度问题。王永亮[2]系统分析了面向城镇连锁经营物流配载与配送组合优化问题的构成要素，研究了多配送中心、多车型、无时间窗限制和软时间窗限制混合、车辆闭环运行的VRP问题。李相勇[3]对车辆路径问题的构成要素和扩展标准作了仔细的讨论和分类，并对各类VRP问题进行了建模和求解。王征[4]对多车场问题作了概述，同时对时间窗问题做了分类，给出了数学模型，并用改进的变邻域搜索算法进行了求解。文章[5]根据城市蔬菜配送公司的实际情况，创新性地同时考虑了车辆路径问题中人力参与较多、多车型、不同车型的固定费用和行驶费用不同且带硬时间窗等问题，并同时考虑车型与任务的相容性。SOLOMO等[6]并未对问题模型进行描述，而是在理论上分析了解决时间窗的车辆路径问题的多种启发式算法。文章[7]则研究了带时间窗的同时收发货的实时车辆路径问题。文献[8-10]则采用了PSO或改进的PSO算法求解。

本文假设要配送的货物是生鲜蔬菜、水果和非处方药品等类型的货物，可以混装，且不考虑多周期配送的问题，将送货地点抽象为社区进行研究。由于客户对生鲜蔬菜和水果的配送优先级的要求有其特殊的时间特征，文中考虑客户的时间窗约束条件和车辆的空间利用率，优化整个配送过程。

1 问题描述与模型

本文将问题描述为简化考虑单配送中心和单车型以及单车程配送的软时间窗问题，且各社区距配送中心的距离以及各社区之间的距离已知。各个社区的货物需求容量已知，每辆车的车型相同，其额定载容量已知，同时已知要求将货物送到的时间窗，要求合理安排车辆的配送路线，使总配送距离最短、车辆利用率最大、超出时间窗的时间总量最少。

为考虑问题的一般性，做如下的模型假设：

1）假定每个社区是一个顾客点，且每个社区点所需的货物不可拆分；2）配送路线对称，且两社区之间的距离即为两地实际地理坐标的几何距离；3）每辆车必须从配送中心发出，最后回到配送中心；4）配送中心的货物总量能满足社区的货物需求量，且各社区的需求量不超过配送车辆的容量；5）忽略卸货时间，且行驶速度始终不变。

建立数学模型如下：

m：配送中心拥有的车辆数

n：顶点数目，n=0表示配送中心，n=1,2,…,n表示各个社区点

dij：各个顶点之间的欧式距离

vi：各个社区的货物需求体积

V：每辆配送车辆的最大载容量 （车型相同）

ETi：配送车辆到达第i个社区的最早时间

LTi：配送车辆到达第i个社区的最晚时间

tij：配送车辆从第i个社区到第j个社区的行驶时间，与距离成比例

Si：配送车辆到达第i个社区的实际时间

上述模型中式 （1）表示目标函数，是车辆总行驶路程最短、车辆空间利用率最大、早到或晚到时间总量最小四个优化目标的综合，由于四个目标的重要性和量纲不同，赋予不同的权重将多目标变为单目标，其中λ1、λ2、λ3、λ4表示各项权重，根据实际要求进行设置，以此来保证优化目标的层次优先级别[2]。 （2）表示每个社区点只能被一辆车服务。 （3）表示每个社区点j只能由来之其他点的所有车中的一辆车来服务。 （4）表示车辆k的配送路线上的社区点所需求货物的体积之和不超过车辆的额定载容量Q。 （5）和 （6）分别表示每辆车必须从车场中心发出来服务社区且服务完其路线上最后一个社区后必须回到车场中心。 （7）表示车辆实际到达每个社区点的时刻。 （8）和 （9）分别表示两个决策变量。

实际中老年人更注重时间上的有效性，因而权重系数λ3、λ4应较大，晚到会降低对老人的服务质量，故λ3比λ4要设置的相对小一些。另外，配送中心自身的成本付出中载容利用率和运输距离，更倾向于优化运输距离，故λ1比λ2要设置的大一些，但两者都要小于λ3、λ4。模型中的权重系数可以根据实际问题中对约束条件的要求程度用层次分析法 （AHP法）求出[2]。

2 方法描述

2.1 PSO算法的引入

对于车辆路径问题，很多时候并不能找到最优解，而只是找到较优解，因为问题的解即各车辆的排列组合的搜索范围过大。由于问题中约束条件较多，当问题规模较大时，要事先得到一个可行解也十分不容易。而启发式算法中PSO算法则可以很好的解决了这个问题，因为PSO算法实际上是基于迭代的优化启发式算法，系统将为其初始化一个随机解，再经过迭代搜索找到最优解。

PSO的优势十分明显，能对解进行并行处理且鲁棒性好、实现简单、精度高、收敛快，也没有许多参数需要调整，能以较大的概率找到优化问题的全局最优解。但同时它也有一定的缺陷，如在大规模问题中易陷入局部最优[8-9]。文献[10]提出的随机惯性权重PSO算法，能有效克服种群中所有粒子共享同一惯性权重的问题，使所有粒子都能向优化方向移动，从而提高PSO的搜索性能，使搜索过程有效地跳出局部最优，搜索全局最优。

2.2 算法具体过程

1）编码方法

一般文献中对于算法的编码都会采用实数编码方法，即对n个社区点，K辆车服务的车辆路径问题，解的维度D=n+K-1。即在顾客点序列中插入K-1个0，则由0分开的序列组成一个车辆行驶路线。实数编码中维度同时依赖于车辆数和顾客点数目。

文中采用另一种编码方式，让维度只依赖顾客点数目，且更大。对n个社区点，K辆车服务的车辆路径问题，将适应度函数对应的自变量即每个粒子设计为一个2n维的向量，分成2个n维向量：前n维Xk表示顺次客户点所使用的车辆编号，后n维Xo表示各社区在对应的路线中的优先级次序。

这样编码直观的显示出服务每个社区车辆编号，也能明确得出每条路线上车辆服务的先后顺序。同时保证每个社区点都能得到车辆的服务，并限制每个社区点仅能由一辆车来服务，从而减少解的可行性计算过程。另外，PSO算法在多维寻优问题中有较好的特性，维数的增大也不会增加计算的复杂性。

2）更新粒子状态

事先约定种群大小为N，则粒子i i=1,2,…,（ ），位置则表示为 xi=xi1,xi2,…,xid

（N 在 d d=1,2,…,2）（n 维解空间中的速度可表示为vi=vi1,vi2,…,vid）

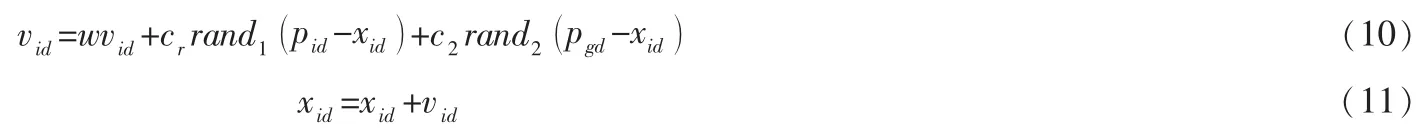
上式中，w表示惯性权重，值越大粒子的全局探索能力越强，值越小粒子的局部挖掘能力越强；c1和c2表示自身和社会的惯性系数，表明粒子自我和群体的学习能力；rand1和rand2是独立的均匀分布于0,［］1 之间的随机数。pid是当前粒子搜索到的历史最佳位置，pgd是整个粒子种群搜索到的历史最佳位置。

文献[10]中提出随机惯性权重粒子群算法，其粒子的状态更新公式为：（ ）。粒子在整个搜索空间内的状态更新将通过下面的两个式子进行更新：

3）适应度计算

文中数学模型，既有载容量的约束，又有时间窗约束，故采用罚函数来处理，将这些约束条件一起写进目标函数中，而粒子的适应度则直接用目标函数表示。利用PSO算法解决VRP问题的具体流程如图1所示。

3 实验结果和分析

本文设计了一个简单的算例，3辆车服务8个社区，并假定每辆车的额定载容量为 V=8。 λ1、 λ2、 λ3、 λ4分别取值为 0.249,0.037,0.32,0.394。 测试如下数据，配送中心和每个社区点的坐标、需求容量数据如表1。

图1 PSO算法流程

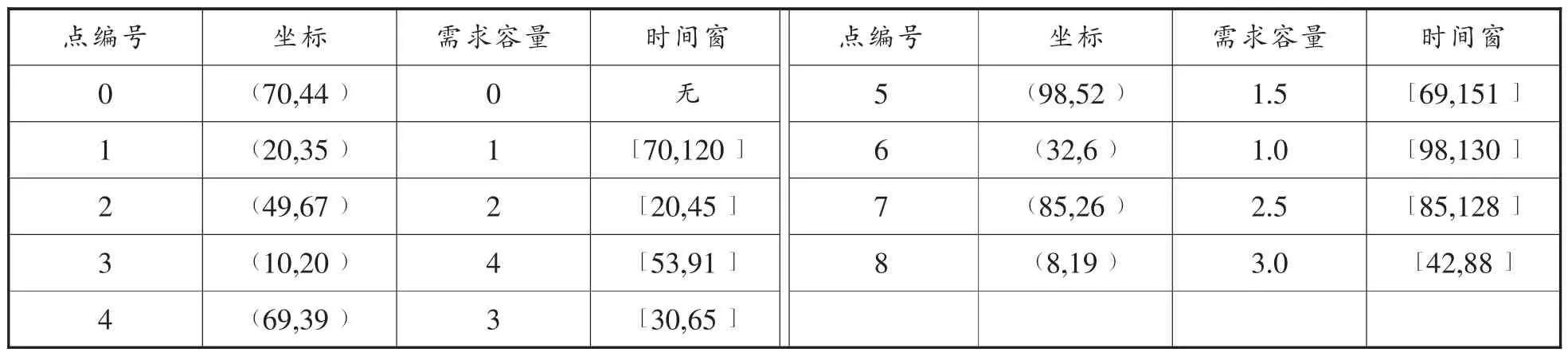
表1 社区的坐标及需求

取粒子数N=50，最大迭代数M=100。w=0.7，c1=1.3和c2=2.8，对随机惯性权重PSO算法取参数k=1，随机进行50次计算。得出的最优结果为：车辆1：0-4-0；车辆2：0-3-8-1-0；车辆3：0-2-6-7-5-0。

将三种方式的计算结果进行比较，如表2所示。

表2 执行50次结果比较表

将三种方式的PSO算法分别执行50次得到的结果分布情况如图2。

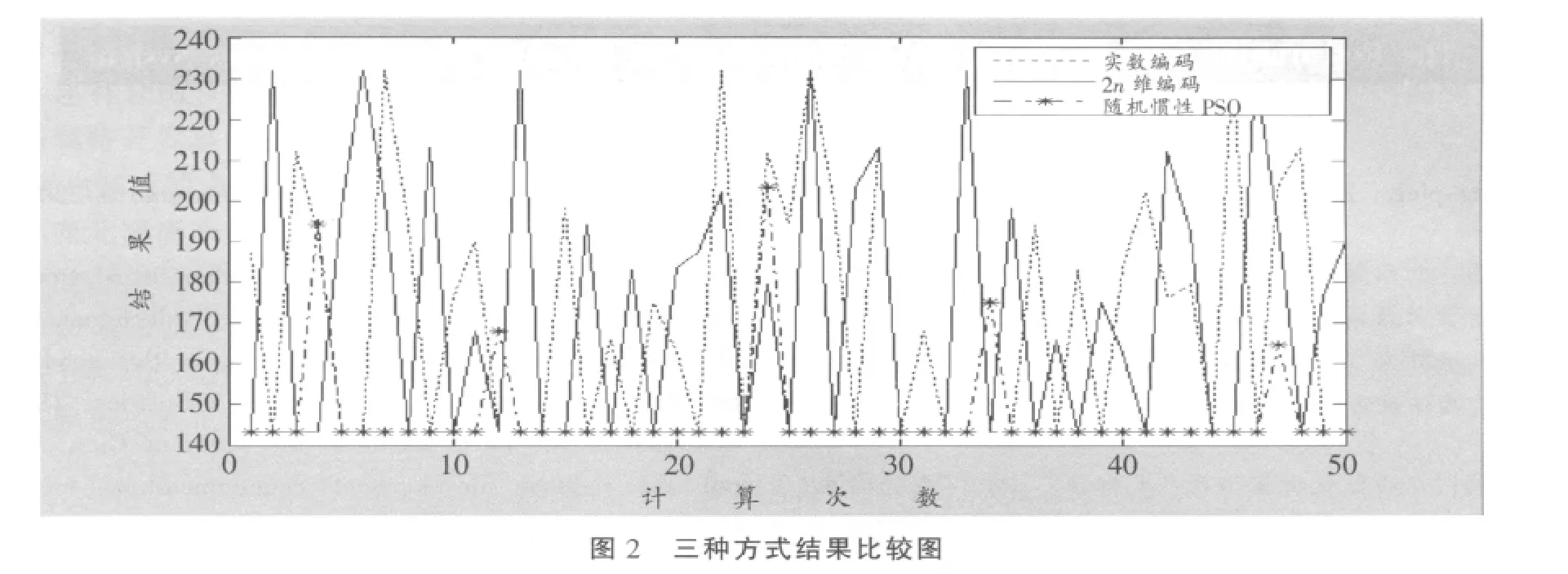
从表2和图2可以得出以下结论：

①两种编码的最优值都是143.2，两种编码并没有太多的优劣性，不管采用何种方式，都可以求出最优值，但搜索成功率都不高。

②标准PSO算法搜索过程达到最优值的次数小于50%，而采用随机惯性权重PSO进行改进后，只有5次没达到最优值，搜索成功率大大提高。

③在相同的执行次数情况下，尽管耗费的时间成本高一些，但随机惯性权重PSO算法达到最优值的次数比标准PSO算法达到的多，所耗费的平均成本也小一些。

综合评估平均搜索时间、平均成本和搜索成功率，随机惯性权重PSO算法对解决VRP问题有较优的效果。

4 结 论

本文针对现今社会呈现的老龄化现象，提出了具有代表性的养老服务中的物流配送问题，并建立了合理的数学模型。同时，对PSO算法的编码方式以及标准PSO和改进PSO进行简单的比较，并求解了一个较为简单的算例。结果表明，随机惯性权重PSO算法对于车辆路径问题的求解有较高的搜索成功率。但本文只对养老配送问题中基本的带时间窗VRP模型进行了研究，未考虑速度对车辆行驶时间的影响，也忽略了混装相容性等约束条件对模型的影响，以后可以对这些方面进行更深入的研究。

[1] 杨锦冬，徐立群.城市物流中心车辆配送配载调度指派模型研究[J].同济大学学报，2004,32(11):1452-1456.

[2] 王永亮.面向连锁经营的物流配载与配送组合优化模型与算法研究[D].北京：北京交通大学 （硕士学位论文），2007.

[3] 李相勇.车辆路径问题模型及算法研究[D].上海：上海交通大学 （博士学位论文），2007.

[4] 王征.多车场带时间窗车辆路径问题的模型和算法[D].大连：大连理工大学 （硕士学位论文），2010.

[5] 肖和山.城市蔬菜配送车辆调度模型与启发式算法研究[J].湘潮，2009(9):56-58.

[6] Marius M.Solomo.Algorithms for the Vehicle Routing and Scheduling Problems with Time Window Constraints[J].Operations Research,1987,35(2):254-266.

[7]Mei-shiang Chang,Shyang-ruey Chen,Che-fu Hsueh.Real-time Vehicle Routing Problem with Time Windows and Simultaneous Delivery/pickup Demands[J].Journal of the Eastern Asia Society for Transportation Studies,2003(5):2273-2286.

[8] 陈严，刘利民.改进型PSO算法在VRP中的应用[J].计算机工程，2011,37(1):170-172.

[9] 黄小燕，文展,等.基于改进PSO的汽车路径优化[J].湘潭大学 （自然科学学报），2009,31(2):166-170.

[10] Zhang Q,Mahfouf M.A New Structure for Particle Swarm Optimization （nPSO） Applicable to Single Objective and Multiobjective Problems[C]∥Proc of the IEEE Int'l IEEE Conf Intelligent Systems,2006.