“人-船”模型的最简初等解法*

邵建新

(石河子大学师范学院 新疆 石河子 832003 )

1 引言

如何掌握和运用“人-船”模型,已有不少文献[1～6]对此进行过讨论.为便于分析讨论,先将问题呈现如下.

【问题】一条质量为M,长为L的小船位于平静的湖面上,一质量为m的人站在船头,最初人和船都静止,如图1．当人从船头走到船尾时,小船相对于湖岸移动了多少距离?(不计水对船的阻力)

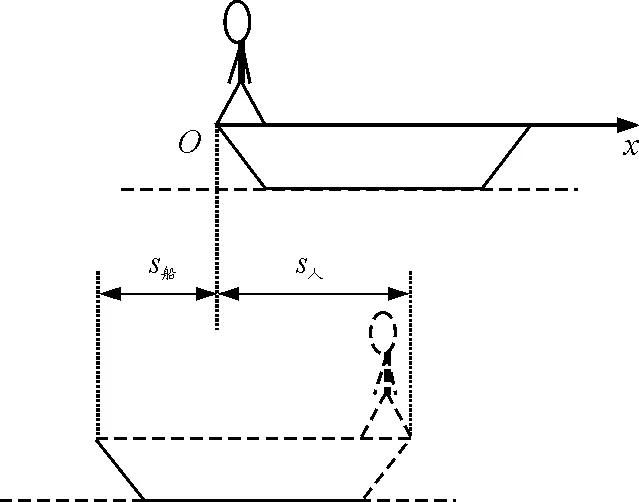
图1

文献[1]在指出文献[2～6]存在模糊与令人费解之处的基础上,对“人-船”问题给出了适合中学物理教学特点的4种解法,并作了详细的、有意义的讨论,使我们受益匪浅.但笔者仍感相关的讨论意犹未尽.

例如,4种解法都存在利用若干假定求解,而且并不是该问题最简的初等解法.笔者认为,利用等效方法求解该问题,物理意义鲜明,而且是最简单的初等解法.

2 文献[1]中四种解法存在的问题

文献[1]结合中学物理教学的特点,探究、概括出4种可行的解法要点归纳如下.

解法1：动量守恒定律+匀变速直线运动速度规律.

将人、船间的摩擦力视作恒力,人、船相对湖岸的运动等效成“匀变速直线运动”,依据匀变速直线运动速度规律,结合人、船位移大小的关系求解.

解法2：动量守恒定律+动能定理+牛顿第三定律.

将人、船间的摩擦力视作恒力,运用动能定理、牛顿第三定律,结合人、船位移大小的关系求解.

解法3：匀变速直线运动位移规律+牛顿第二、三定律.

将人、船间的摩擦力视作恒力．人、船相对湖岸做匀变速直线运动．依据匀变速直线运动位移规律和牛顿第二、三定律,结合人、船位移大小的关系求解.

解法4：动量守恒定律+匀变速直线运动速度-位移规律+牛顿第二、三定律.

将人、船间的摩擦力视作恒力,人、船相对湖岸做匀变速直线运动,依据匀变速直线运动速度-位移规律，牛顿第二、三定律，动量守恒定律,结合人、船位移大小的关系求解.

不难看出,上述4种解法都离不开“人、船间的摩擦力为恒力”和“人、船相对湖岸做匀变速直线运动”这两条假设.实际上,假定“人、船间的摩擦力为恒力”必定导致“人、船相对湖岸做匀变速直线运动”这一结论.而这一假设未必与实际情况相符,学生也会对此提出疑问,为什么要做如此假定？这个假定是否必要？如果这些假定不合理,为什么在这些假定下所得的结果又是正确的呢？

3 大学普通物理的解法

为了弄清“人-船”模型问题的物理实质,我们先用大学普通物理的方法求解该问题.

将人、船选作系统.建立如图1所示的坐标系.设任意时刻t,人和船相对于湖岸的速度大小分别是v1，v2(假定船与人的运动方向相反),因系统水平方向所受合外力为零,故水平方向系统的动量守恒.依据动量守恒定律可得

0=mv1+M(-v2)

(1)

设人从船头走到船尾所用的时间是T,将式(1)两边同时对时间t积分,有

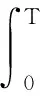
(2)

以s人,s船分别表示人、船相对湖岸的位移大小,则

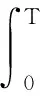
(3)

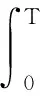
(4)

将式(3)、(4)代入式(2),有

ms人-Ms船=0

(5)

依据位移合成定理,有

s人+s船=L

(6)

联立式(5)、(6)求解可得

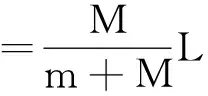
(7)

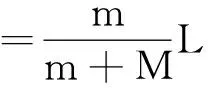
(8)

当然,该问题还可以用质心运动定律求解.因人和船组成的系统在水平方向不受外力,因而，在水平方向质心的速度不变.又因为系统的质心原来静止,所以，在人走动的过程中质心始终静止,所以，质心的坐标值不变,据此可以列一个方程,再结合人、船位移大小的关系联立求解即可.具体解法参看文献[7].

4 分析讨论

4.1 人和船相对湖岸的位移和人的运动方式无关

从上面的求解过程不难看出,如果忽略船在行进过程中所受的阻力,人和船组成的系统总动量在任何时刻均为零，即任何时刻人对水和船对水的运动形式相同而运动方向相反，也即人动船动,人加速船加速,人匀速船匀速,人减速船减速,人停船停.在某段时间内,人和船相对湖岸位移的大小和人的运动方式无关,而只与人和船的质量及船的长度有关.

由此就可以理解文献[1]给出的4种解法中，为什么在不同的假定下会有相同的结果了.

4.2 人-船问题有初等解法吗

正如文献[8]所指出的那样,运用动量守恒定律的目的是，避开所研究问题的系统经历过程的细节和系统内可能复杂的相互作用,直接考虑系统过程始末态的动量,从而使问题解决起来更简捷.因此,“人-船”模型问题的求解首选动量守恒定律.然而,从以上求解可知,由动量守恒,即式(1)求位移,必须用积分.为了避免积分,文献[4～6]引入平均动量的概念求解是不正确的.文献[3]引入平均速度的概念求解

mv1-Mv2=0

(9)

s人=v1t

(10)

s船=v2t

(11)

s人+s船=L

(12)

即式(9)～(11)中的v1,v2分别是人和小船的平均速度,求得的结果是正确的.

显然,式(10)～(12)是正确的.而式(9)则令人费解.因为动量守恒定律中涉及的动量均是指系统某时刻的动量,因而，不能用质量乘以平均速度表示该动量.

在4.1的讨论中，我们已经指出,人和船相对湖岸位移的大小和人的运动方式无关.既然与人的运动方式无关,从求解问题的角度来看，关于人运动方式的各种假定都是可以的.当然，假定人和船的运动是匀速直线运动一定是可以的(尽管这种假定不符合实际情况).问题是式(9)仍然正确吗？如果式(9)错了,那为什么联立式(9)～(12)求得的结果又是正确的呢？如果不错,其物理意义是什么呢？

笔者认为,用等效法处理这类问题是最简单的方法,但用该方法需要对匀速直线运动这个大家都认为很简单的理想模型以及平均速度的物理意义有深刻的理解和认识.

4.3 匀速直线运动及变速直线运动平均速度的物理意义

匀速直线运动的严格定义是,在任何相等的时间内通过的位移都相等.也就是说,在物体运动所经历的时间段内,任取两个时间段t1，t2,若两时间段内发生的位移分别是s1，s2,则一定有

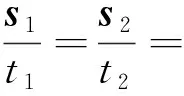
于是，将匀速直线运动的速度定义为

用来描述物体运动的快慢.

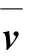
即在变速直线运动中,运动物体的位移和所用时间的比值,叫做这段时间内的平均速度.引入平均速度的概念,尽管是粗略描写,但效果相当,而且定义了平均速度后,对任何变速直线运动，上式都成立.

另外,人们往往会忽略匀速直线运动的一个基本特征,任意时刻的瞬时速度等于其速度v.也许正是这个忽略,导致人们长期没有发现解决此类问题最简单的初等解法.

5 最简单的初等解法

通过4.3的分析不难得到人、船问题的最简单的初等解法.设人从船头走到船尾所用时间是T,人和船做的是变速直线运动,则人和船的平均速度分别是

(13)

(14)

联立式(12)与(14)求解可得

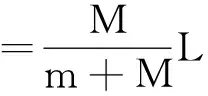
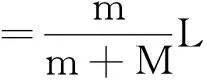
式(14)变形后可得

ms人-Ms船=0

(15)

式(15)就是此类问题中动量守恒定律的等效表达式.

由此可见,式(9)并没有错误,只是以往的文献中要么直接给出不做推导,要么诠释有误.

在物理教学和物理研究活动中,理想模型法和等效方法是常用的分析、解决物理问题非常有效的方法,将两者有机结合并灵活运用,也是学生的物理思想和物理思维能力提升的一个重要途径.

参考文献

1 何述平.“人-船”模型的教学研究.物理教师,2012,33(6):13～15

2 阎金铎,田世昆.中学物理教学概论(第2版).北京：高等教育出版社,2003.151

3 刘炳升.走进高中新课改：物理教师必读.南京：南京师范大学出版社,2005．149～153

4 陈刚,舒信隆.新编物理教学论.上海：华东师范大学出版社,2006.124～128

5 陈刚.物理教学设计.上海：华东师范大学出版社,2009.144～146

6 陈刚,舒信隆．问题图式在物理问题解决教学中的应用．课程·教材·教法,2009,29(7)：57～61

7 张三慧.大学物理学(第一册力学)(第2版).北京：清华大学出版社,1999.152～153

8 漆安慎,杜婵英.力学基础.北京:高等教育出版社,1982.173