“补偿法”在普通物理教学中的应用

赵 强 韩春杰

(石家庄机械化步兵学院 河北 石家庄 050083)

大学物理中所学的定理、定律或公式通常是解决具有对称性分布的物理问题，而在解题过程中，常常遇到某些物理量分布不对称性的问题.如何利用已有的知识解决这些难题，是学生深感困惑的事情.利用补偿法巧妙地将一些不对称分布问题假设在一定条件下变为对称分布，从而，使原问题的求解过程简化或通过补偿消除某些非对称因素，将复杂的物理问题由难变易，由繁变简.在计算挖空物体的转动惯量、带电体的电场强度和载流导体的磁感应强度等问题时常常用到补偿法求解.

1 求刚体的转动惯量

解析：本题如根据转动惯量的定义积分计算比较困难.但用“补偿法”(或称“负质量法”)计算，就简单得多.设想在带孔圆盘的每个小孔处填充质量为正的和负的且相等的小圆盘, 这样，并不改变原来的质量分布[2], 但形成了正质量的大圆盘和两个负质量的小圆盘的组合体, 它们的转动惯量都可按公式计算, 带孔圆盘的转动惯量即可求得.

正质量的大圆盘对盘心O轴的转动惯量为

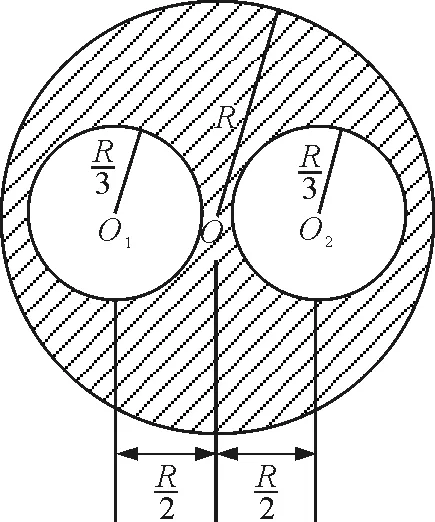
图1

两个负质量的小圆盘对O轴的转动惯量为

所以带孔圆盘对O轴的转动惯量为

2 求解带电体的电场强度

【例2】如图2所示，在电荷体密度为ρ的均匀带电球体中，存在一个球形空腔，若将带电体球心O指向空腔球心O′的矢量用a表示，试求球形空腔中任一点的电场强度[3].

图2

解析：本题所给的带电体的电荷分布不满足球对称，它的电场分布也不是球对称分布，因此,无法用高斯定理求其电场分布，也无法用点电荷场强公式由积分法求得，但可用场强的叠加原理，即补偿法进行求解.具体方法是挖去空腔球体的电场强度加上补有同样电荷体密度的空腔球体的电场强度，就等于整个球体的电场强度.由于整个球体和补有电荷的空腔球体的电场强度很容易求出，所以,挖去空腔球体的电场强度就可以求出.

挖去空腔的带电球体在电学上等效于一个完整的、电荷体密度为ρ的均匀带电球体和一个电荷体密度为-ρ的空腔球体.这样，利用电场强度的叠加原理，挖去空腔的带电球体的电场强度就可以计算.

均匀带电球体内部一点的电场强度，由高斯定理可得

由几何关系可得

r1-r2=a

所以

3 求载流导体的磁场分布

【例3】如图3所示，一根半径为R的无限长载流直导体，在导体上有一半径为R′的圆柱形空腔，该空腔的轴与直导体的轴平行，两轴相距为d(d>R′).导体中有电流I沿轴向流过，并均匀分布在横截面上.试求空心部分轴线上的磁感应强度的大小[4].

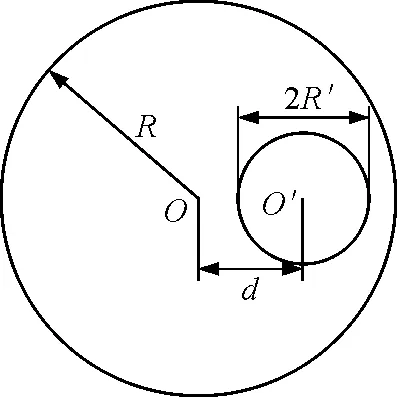
图3

解析：题中给出的电流为非对称分布，产生的磁场分布不具有轴对称性，因而不能用安培环路定理直接求解.但可以利用补偿法求空腔内的磁场分布.将题中的载流导体视作两个半径分别为R和R′的实心圆柱形导体，其电流密度j均为

但两导体上电流的流向相反.这相当于在原导体空腔处补上电流密度相同、电流方向相反的两束电流，此时空腔内任一点的磁感强度为B=B1+B2.

由安培环路定理知，空心圆柱体在其轴心处的磁感应强度

实心圆柱体在O′处的磁感应强度可由安培环路定理求出

所以

参考文献

1 康颖．大学物理(下册)．北京：科学出版社，2006.152

2 程国均．大学物理学教程．北京：科学出版社，2002.156

3 马文蔚．物理学(中册)．北京：高等教育出版社，2002.53

4 张三慧．大学物理学(第三册)．北京：清华大学出版社，2000.180