运用双曲线知识求解物理问题
2013-01-11杨国平
杨国平
(绍兴市第一中学 浙江 绍兴 312000)
1 双曲线的几何特性
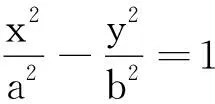
双曲线在物理竞赛中时有涉及,其主要的几何性质有:
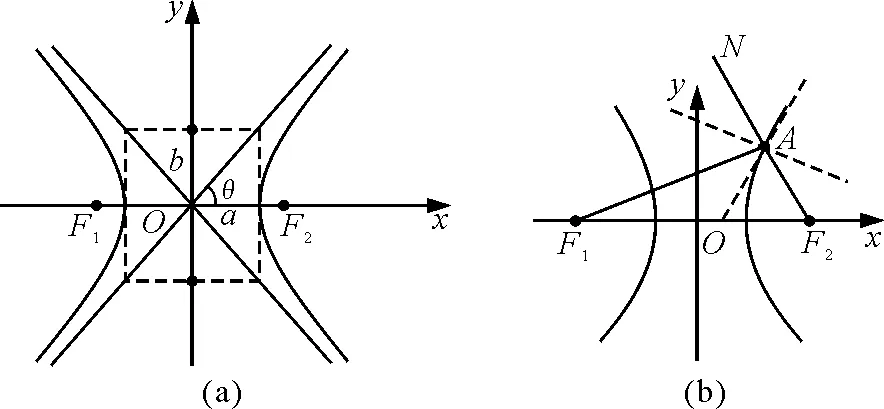
图1
(3)从焦点发出的光经双曲线镜面反射,光线反向延长线会聚于另一焦点,这是双曲线的光学性质.如图1(b)所示,双曲线在A点的法线是∠F1AN的角平分线;过A点的切线AO是∠F1AF2的角平分线.
2 以双曲线为载体的竞赛题
【例1】 图2(a)为某一报告厅主席台的平面图,AB是讲台,S1和S2是与讲台上话筒等高的喇叭,它们之间的相互位置和尺寸如图所示.报告者的声音放大后经喇叭传回话筒再次放大时可能会产生啸叫,为了避免啸叫,话筒最好摆放在讲台上适当的位置.已知空气中声速为340 m/s,若报告人声音的频率为136 Hz,问讲台上这些位置在哪里?
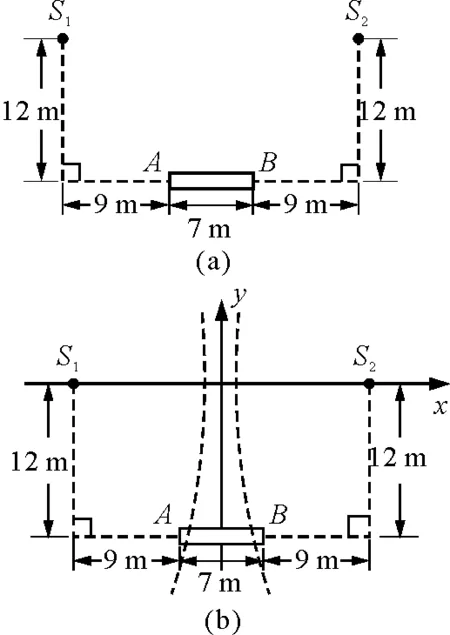
图2
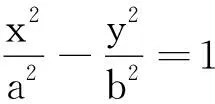
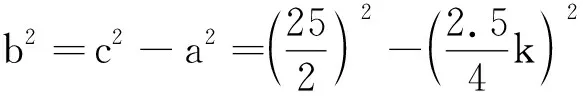
代入得
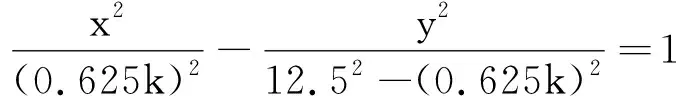
它与直线方程y= -12的交点即为干涉相消点的位置,代入后有
令k=1,解得x≈0.87 m;k=3,x≈2.61 m;k=5,x≈4.40 m(已在B点以外).
由对称性知,与y轴对称的左侧讲台上也有两个位置是干涉相消点.
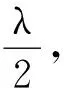
【例2】 两块相同的大玻璃平板夹一个小角度φ,这样就在两板之间形成一个楔形的空气膜.把两块板竖直地插入水面,水会沿着玻璃板面爬升一定的高度,试判断稳定后两板之间的液面边缘(即与玻璃板面的交线)形状.
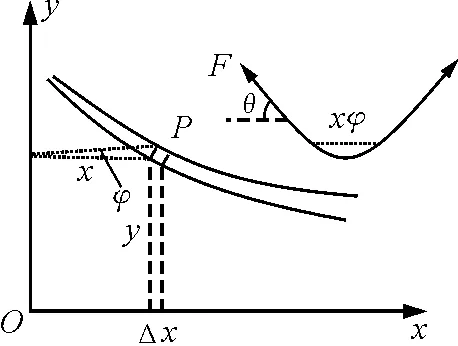
图3
解析:建立图3所示的直角坐标系xOy,其中y轴为两板的公共边,x轴落在水面上.在曲面上任取一点P(x,y),在其周围取一长方体(实为四棱柱)微元,高为y,长为Δx→0,宽为xφ,稳定后该微元的重力Δmg与表面张力F张平衡.
其中F张=2σΔx·cosθ(θ为水与玻璃的接触角),微元质量Δm=ρ·ΔV=ρ·Δx·xφ·y.代入后
2σΔx·cosθ=ρΔx·xφy·g
化简得
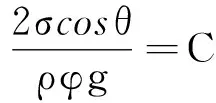
【例3】如图4(a)所示,长为L的细棒AB均匀带电,在xOy平面上的电场线方程为
A.圆 B.椭圆 C.抛物线 D.双曲线
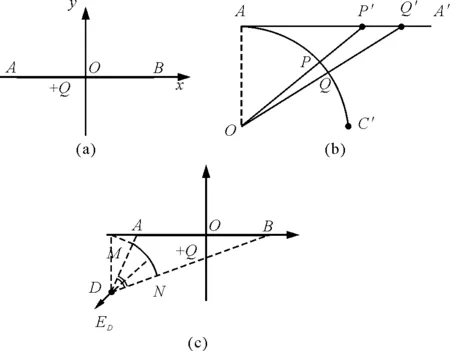
图4
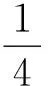
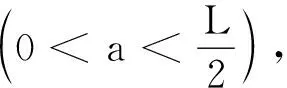
【例4】一人造卫星绕地球做椭圆运动,其半长轴和半短轴分别为a和b.当该人造卫星在轨道的远地点时,突然以很大的能量ΔE沿卫星运行方向从卫星上发射出一个质量为m的太空探测器,该探测器在地球引力作用下做双曲线运动,并以地心为此双曲线的焦点,实半轴的长度正好等于原来椭圆远地点到地心的距离.求ΔE.设地球的质量为M,万有引力常量G已知,不计地球以外星体的影响.
解析:显然ΔE=E′-E,式中E′为探测器在双曲线轨道上的能量,E为在椭圆轨道上的能量.在椭圆轨道上机械能守恒,设远地点(如图5中的A点)和近地点的速度分别为v1和v2,有
(1)
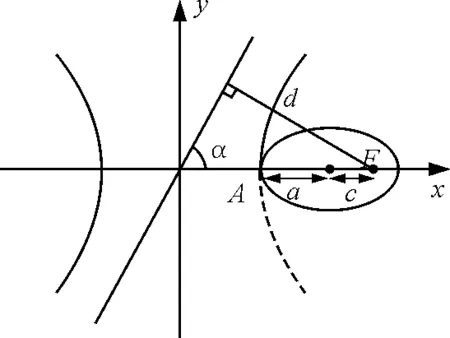
图5
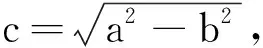
(2)
联立式(1)、(2)解得
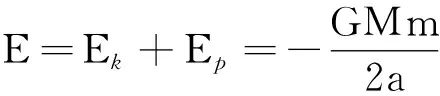
在双曲线轨道上,设探测器在切点处的速度变为v0(未知),在无穷远处的速度为v∞,则由机械能守恒定律可得
(3)
又根据角动量守恒定律,有
mvd=mv0(a+c)
(4)
图中d= 2 (a+c) sinα,α为图中双曲线的一条渐近线的倾角,渐近线方程为
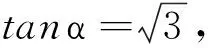
(5)
联立式(3)、(4)、(5)
解得
则
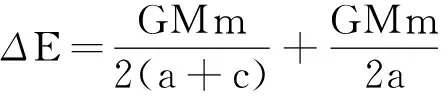
参考文献
1 杨国平.用等效替代法求线电荷分布的场强.物理实验(中学部分),23(1):35~38
