新型钢管混凝土柱方形环梁节点有限元分析
2013-01-11聂肃非单瑶嘉
葛 森, 聂肃非, 单瑶嘉
(华中科技大学 土木工程与力学学院, 湖北 武汉 430074)
关于钢管混凝土柱与RC梁连接节点的做法是设计和施工中较为棘手的问题,文献[1]中提出了环梁节点,其构造是在框架梁截面高度处围绕钢管混凝土柱设置圆环形钢筋混凝土梁,将框架梁纵筋弯折锚固于环梁内,并沿钢管围焊一道或多道钢筋作为抗剪构件。因施工简便和经济效益明显,环梁节点受到很大关注,但至今仍未有一个统一可靠的承载力设计方法[2],其原因可能与环梁节点连接形式存在的某些不足相关,例如,环梁截面上的弯矩、扭矩随着截面角度的不同而持续改变,致使截面受力十分复杂,并且此类截面是否满足平截面假设也无相关理论或试验支持,使用《混凝土结构设计规范》[3]中的方法求解截面承载力未必可靠。另外,圆形环梁纵筋在混凝土约束下局部范围内受到框架梁端荷载作用时,其内部应力的传递受到一定程度的阻碍,使得环梁纵筋应力分布不均匀,某些部位较早出现屈服。
鉴于此,本文在参考RC圆环梁节点以及文献[4]中建议的几类节点形式的基础上,提出方形环梁节点,通过实体有限元建模计算,分析了方形环梁节点的传力机理,并与圆形环梁节点相关结果进行对比,最后根据节点的受力特点对抗弯配筋的设计进行了研究。
1 方形环梁节点构造及有限元模型
1.1 方形环梁节点的构造
方形环梁节点构造如图1所示。方形主要针对环梁纵筋而言,在各支框架梁之间呈直线分布。其中设置抗剪环用于抵抗梁端剪力的方法同圆形环梁节点相同,不同之处在于图1(a)所示虚线部分表示的环梁纵筋的分布形态,其钢筋在各框架梁之间直线相连,与框架梁相交处则垂直于框架梁轴线。在环梁内侧最短纵筋长度范围内可以正常配置箍筋,而距框架梁较近的区域,宜在框架梁纵筋和环梁纵筋的交接点处配置适当箍筋,此类箍筋只能连接该节点与其环外侧的环梁纵筋。

图1 方形环梁节点
1.2 有限元模型的建立及加载

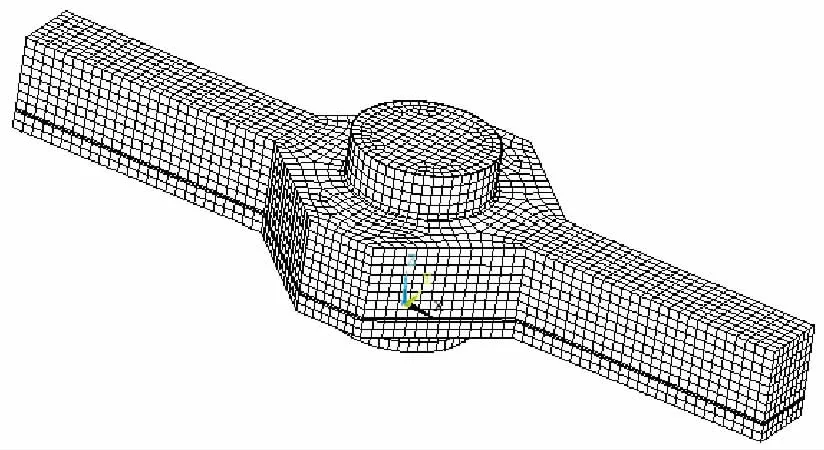
图2 方形环梁节点混凝土有限元模型

图3 方形环梁节点钢筋有限元模型
另外,为了对比圆形环梁和方形环梁的受力特点,同时验证非线性有限元计算的准确性,本文也选取了文献[1]中圆形环梁节点E1试验模型进行建模计算,其环梁截面尺寸为400×550,配置箍筋φ14@250,其他尺寸与配筋量同上述方形节点模型一致。
计算取1/4模型,约束柱底层节点所有自由度并限制顶层节点x、y方向位移,首先在柱顶施加1000 kN的压力维持稳定同时模拟钢管混凝土柱的受力状态,然后分别施加剪力和弯矩进行计算。计算剪力时在与框架梁相交的环梁区域顶部施加500 kN的压力;计算弯矩作用时在梁端施加竖直向下的压力500 kN,在环梁节点处将产生相应的弯矩。计算时采用力收敛准则,将精度调至5%,使用Newton-Raphson迭代并打开线性搜索功能。
2 梁端荷载-位移计算结果对比
对两种节点框架梁梁端施加垂直压力,根据计算结果绘制了梁端荷载-位移曲线,并与文献[1]中E1模型试验得到的圆形环梁节点荷载位移曲线进行比较,如图4所示,可以看到圆形环梁节点计算结果与试验结果吻合较好,有限元计算圆形环梁节点梁端荷载为305 kN后便不再收敛,试验测得极限荷载为310 kN。因此可以用ANSYS对本文提出的方形节点进行仿真分析。另外图中还给出了方形环梁节点的荷载-位移曲线,从图中看出在环梁纵筋量相同的情况下,方形环梁节点具有较高的承载能力,因此,值得对其作进一步的研究。
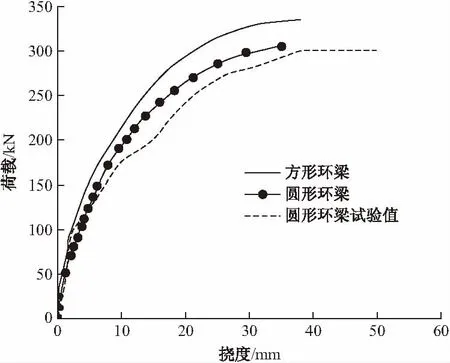
图4 环梁节点试验与计算的梁端荷载-位移曲线
3 方形环梁直剪作用分析
对于圆形环梁节点,剪力将通过抗剪环以及环梁与钢管壁的静摩擦力来承担,为了研究方形节点是否有同样的抗剪机理,取1/4方形环梁节点的抗剪环并查看其应力分布。图5绘制了抗剪环截面上平均剪应力和Mises等效应力沿着抗剪环长度的分布曲线,长度起始于抗剪环对应的框架梁的轴线位置。从图中可以看出,抗剪环竖向剪应力在框架梁宽度对应的范围内较大,然后逐渐减小,等效应力也表现同样的规律,说明抗剪环在框架梁宽度范围内承担较大的作用力。另外抗剪环在整个施加剪力过程中,虽然在与钢管的连接处局部剪应力较大,但其截面平均剪应力相对较小,说明在直剪作用下,环梁与钢管壁之间的摩擦力在承担剪力作用时依然占有较大比例。

图5 方形环梁节点抗剪环剪应力及等效应力分布
4 方形环梁弯矩作用分析
通过有限元计算查看方形环梁节点在弯矩作用下裂缝的扩展、环梁混凝土及钢筋的应力分布等结果,并通过相应对比分析了方形环梁节点的抗弯机理与传力性能。
4.1 裂缝的扩展
计算后发现,首道混凝土裂缝同时在框架梁与环梁的交界处顶层和环梁的最窄截面顶层出现,方向分别垂直框架梁轴线和沿着钢管混凝土径向方向,并且都是由截面弯矩所引起的拉裂缝。随着荷载的增加,裂缝分别向两边均匀扩散,而框架梁两侧的环梁截面较晚出现抗扭裂缝,这与圆形环梁节点较早出现在框架梁两侧的抗扭斜裂缝不同[5],钢筋混凝土结构本身的抗扭性能差,延迟抗扭裂缝的产生对节点是有利的。
4.2 环梁混凝土的应力分布
ANSYS计算不收敛后停止运行,取出最后一个荷载子步所对应的1/2个方形环梁混凝土各个面的应力分布如图6~8所示。从图6(a)中所显示的x方向(x方向为平行于框架梁轴线方向)应力颜色图可以看出环梁底部压应力主要分布在与框架梁相交部分的环梁混凝土上,并且压应力在框架梁宽度范围外迅速减小。图6(b)、(c)显示了环梁下部混凝土其他两个方向应力的分布情况,从图中可以看出其他两个方向应力都很小,说明环梁下部混凝土在荷载作用下基本呈单向受压状态,且压应力主要分布在框架梁宽度范围内。

图6 方形环梁底面x、y、z方向应力分布
图7(a)为方形环梁顶面等效应力分布图,可以看出方形环梁上表面应力较为均匀,整个环面的应力大小没有明显的变化趋势。图7(b)中圆形环梁应力分布呈现一定的规律,其拉应力集中在框架梁两侧扇形区域内,对于混凝土而言便更加容易开裂。图8显示了方形环梁侧面的应力分布,可以看出在与框架梁相交侧面的中间部位以及斜侧面的下角部位,都出现了较大范围的小应力区域,而就整个环梁侧面来讲应力也普遍较小,实际也反映了环梁受到的扭矩较小。
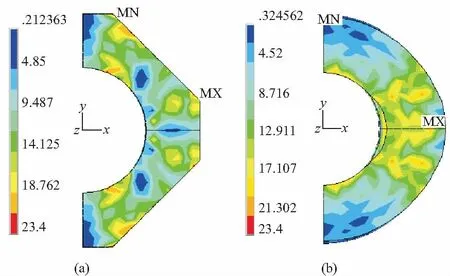
图7 方形与圆形环梁顶面等效应力分布

图8 方形环梁侧面等效应力分布
4.3 环梁钢筋的应力分布
在整个计算过程中,两种环梁上部受拉纵筋应力都较大,但方形环梁应力分布更均匀,如图9所示,方形环梁上层纵筋的应力沿着钢筋长度方向没有一个较为明显的变化趋势,这与圆形环梁节点上部纵筋的应力分布不同,圆形环梁上层纵筋的应力分布在整个加载过程中呈现出较为典型的规律性,从图10中可以看到黑色方框所圈圆形环梁区域应力较大,这也是圆形环梁主裂缝在框架梁两侧呈“八”字形[6]展开的原因。

图9 方形环梁上层纵筋应力分布
由以上分析可知,方形环梁节点的传力机理基本同圆形环梁一致,大部分梁端负弯矩通过环梁上部受拉的纵筋和下部受压混凝土形成抵抗力矩来承担,小部分则转化成环梁自身扭矩,然而对其混凝土和钢筋的应力分布可以看出,方形环梁受力更加均匀,排列方向不变的纵筋更加有利于内部应力的传递。
5 方形环梁节点抗弯承载力设计方法
5.1 方形环梁抗弯承载力计算分析
为了方便分析环梁受力状态,忽略内环纵筋垂直面与钢管柱外壁之间混凝土的几何影响,将环梁分成3个区域,如图11所示,S1为环梁与框架梁相交的区域,S2为紧靠框架梁侧面的三角形区域,S3为环梁最里层纵筋为边所对应的矩形区域。b为环梁宽度,w为框架梁宽度,r为钢管半径。

图11 方形环梁局部构造
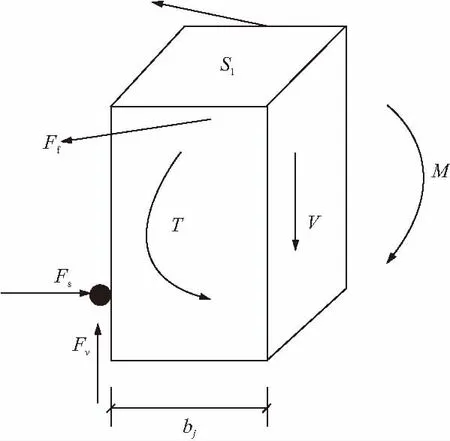
图12 S1受力状态
取出S1如图12所示,其中V、M为梁端剪力和弯矩,Fs为刚管混凝土的水平挤压力,Fv为钢管壁向上的静摩擦力和抗剪环承担的压力之和,Ff为上部环梁纵筋的斜向拉力,T为S1前后截面的扭矩。根据抗弯机理,环梁所受总弯矩V·bj+M分为两个部分:
V·bj+M=2T+Msr
(1)
其中Msr为Fs与Ff在框架梁轴线方向的分力所形成的弯矩,由于Fs是由框架梁下部混凝土受压传递给钢管的压力,假设Fs合力点与框架梁受弯截面下部受压混凝土的合力点等高,则有:
Msr=Fs(h0-x/2)
(2)
(3)
其中h0为框架梁截面有效高度,x为框架梁正截面受弯时混凝土受压高度。若知道Fs大小即可得到Msr部分所需要的上部纵筋配筋量,大小为:
(4)
其中fy为环梁上部纵筋的抗拉设计强度。另一部分梁端弯矩转化成环梁扭矩,有:
T=[(V·bj+M)-Msr]/2
(5)
通过上式结合GB 50010-2010《混凝土结构设计规范》[3]有关规定对S1区域配置箍筋。T通过S2传递到S3后在S3截面形成的扭矩和弯矩,其大小相等:
(6)
通过上式结合《混凝土结构设计规范》[3]关于抗弯抗扭承载力计算公式可对S3区域配置满足要求的纵筋和箍筋,最后结合Az1即可完成环梁所有配筋。
因此关键在于了解Fs大小及其规律。取出Fs所对应的面,通过全截面正应力对截面进行积分记得到:
(7)
在各个荷载子步下计算Fs得到了图13关于Fs与梁端弯矩关系,弯矩0时对应的Fs为一个较小值是由于柱端施加压力环梁受钢管柱径向压力所致,图中可以看出Fs与梁端弯矩基本呈线性关系,将图中曲线线性拟合计算得到:
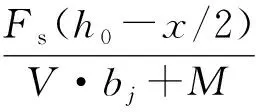
(8)

图13 Fs与框架梁端弯矩关系
此式表明环梁纵筋与钢管壁压力之间形成的抵抗弯矩占梁端总弯矩的62.5%,则框架梁两侧分别抵抗的扭矩为18.75%,相比而言此值较小。综上,在梁端剪力和弯矩给定的情况下即可配置相应的纵筋和箍筋。
5.2 比例系数影响因素的正交试验法分析
上面有限元计算得到的0.625是弯矩分配的比例系数,其大小将受到节点几何尺寸的影响。为了讨论节点主要几何参数对此系数的影响规律,本文选取4个可能影响比例系数大小的独立几何参数,分别为刚管混凝土柱半径、环梁截面高度和宽度以及框架梁宽度,考虑每个参数3个水平变化,选用L9(34)正交试验,具体模型尺寸以及计算结果在下表1所列。
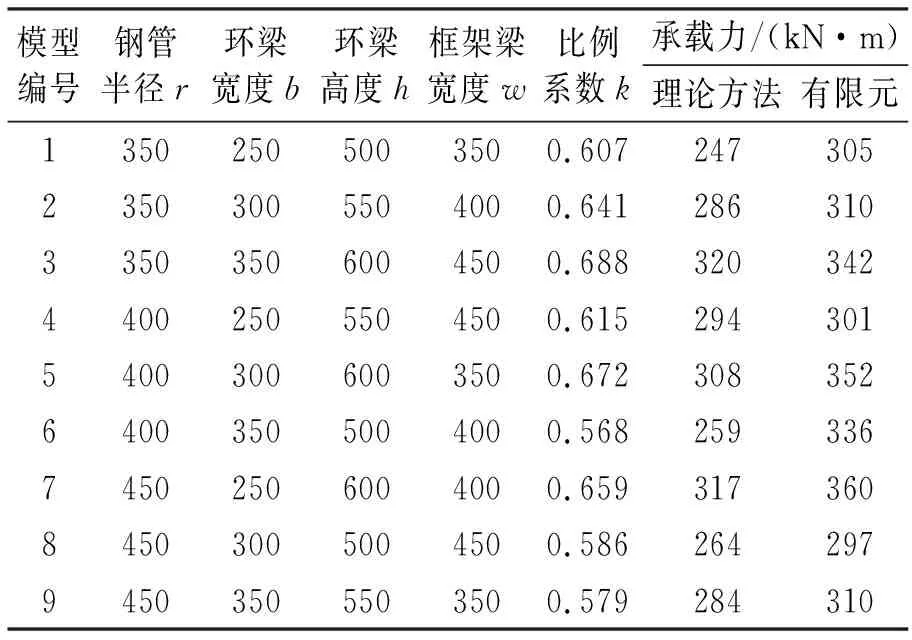
表1 正交设计表
注:理论计算方法通过实配钢筋面积反算极限承载力可先计算出抵抗弯矩和截面抗扭承载力的大小,然后比较它们之间的比值与k(1-k)的大小,取较小者通过比例系数即可求出极限承载力。
图14描述了各个因素对比例系数影响的水平趋势,从图中可以直接看出增加环梁高度、框架梁宽度都一定程度的提高了比例系数,表明对弯矩分配给钢管和环梁纵筋有促进作用;而增大环梁宽度、钢管半径则减小了比例系数,说明对弯矩分配给环梁抗扭有积极作用。因此,在特定的情况下可以通过改变环梁节点中环梁的尺寸来优化节点的设计。另外,通过对各因素极差的计算可得敏感性程度为:
h>r>b>w
(7)
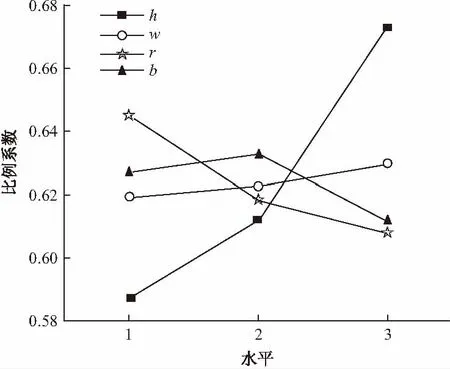
图14 各因素水平影响趋势
对上述计算结果的回归分析,由于难以从数据中直接观察出回归函数的类形,此处使用多项式对数据进行回归,最后得到比例系数为:
k=2.67+0.0031b-0.0072b2-4.8333×10-4h-0.003h2-5.466×10-6w+7.33×10-6w2+7.33×10-7r+3.33×10-6r2
6 结 论
(1)方形环梁节点具有与圆形环梁节点相同的抗剪、抗弯机理:通过抗剪环与钢管壁的静摩擦力来承担剪力;通过环梁纵筋受拉、钢管柱受压形成抵抗力矩和环梁的扭转来承担弯矩,两者分担弯矩的大小受到节点几何尺寸的影响,其中环梁高度影响最为明显,因此,可以通过相关的尺寸优化设计使节点配筋更加合理。
(2)方形环梁节点由于在框架梁之间的环梁纵筋呈直线分布,有利于内部应力的传递,使方形环梁应力分布较圆形而言更加均匀,因此提高了方形环梁的承载能力。
(3)方形环梁节点由于在相应的范围内环梁截面方向不变,容易分析截面受力状态,使得提出更合理、更可靠的承载力设计方法相对简单,从而在工程上应用更有依据。
[1] 方小丹,李少云,陈爱军.新型钢管混凝土柱节点的试验研究[J].建筑结构学报,1999,20(5):1-15.
[2] 谢玉芳.钢管混凝土柱-钢筋混凝土环梁式节点抗弯机理分析[J].安徽建筑工业学院学报(自然科学版),2012,20(2):39-42.
[3] GB 50010-2002,混凝土结构设计规范[S].
[4] 黄汉炎,梁宇行,李曦新,等.钢管混凝土柱、RC梁板节点拟静力三向加载试验研究[J].建筑结构学报,2001,22(6):3-13.
[5] 魏 琏,王志远,王 森,等.钢管混泥土柱-RC环梁节点计算方法的研究[J].建筑结构,2008,38(3):29-33.
[6] 方小丹,黄圣钧,李少云,等.RC梁-圆钢管混凝土柱节点环梁承载力设计方法[J].建筑结构学报,2008,29(5):20-33.
