钢筋混凝土框架结构地震易损性分析
2013-01-11汪立生龙晓鸿
廖 萍, 汪立生, 龙晓鸿
(1. 江苏泛亚联合建筑设计有限公司, 江苏 无锡 214005;2. 机械工业第一设计研究院, 安徽 合肥 230601;3. 华中科技大学 土木工程与力学学院, 湖北 武汉 430074)
随着全概率第二代基于性能的结构抗震设计方法的提出,结构地震易损性分析已经成为地震工程界和结构工程界的研究热点[1]。结构地震易损性曲线可以通过经验方法和分析方法得到[2]。经验方法得到的易损性曲线一般是基于以往地震的破坏报告;而分析方法得到的易损性曲线是通过对结构地震反应的计算获得。
钢筋混凝土框架结构作为城市建筑的主体,估计这些建筑在地震中出现的各种破坏状态的分布概率,对地震防灾规划和地震灾害应急具有重要价值。国内外对于钢筋混凝土建筑的易损性分析进行了大量的研究。吕大刚等[3]以一榀五层三跨钢筋混凝土框架结构为例,分别采用传统云图法和改进云图法对其进行概率地震需求分析,得到了结构的概率地震需求模型、地震需求易损性曲线和地震需求危险性曲线。吴巧云等[4]综合考虑地震动峰值加速度及阻尼比为5%的谱加速度,考虑近场及远场地震的不同性质,对一钢筋混凝土框架房屋进行地震易损性分析。Schotanus等[5]对钢筋混凝土框架结构时变系统可靠度问题的地震易损性进行了分析。Sasani等[6]通过建立结构构件的Bayesian 概率能力模型,分析了桥梁结构和钢筋混凝土墙的地震易损性。
本文以一榀RC框架结构为研究对象,选取8条远场地震动记录,分别以层间位移角和顶点位移角为地震需求目标参数,选择PGA为地震动输入参数,采用SAP2000程序进行非线性有限元分析,从而建立钢筋混凝土框架结构在远震和近震作用下的易损性曲线。
1 地震易损性分析步骤
地震易损性分析是地震风险分析的重要内容之一,地震易损性描述的是结构在确定强度的地震作用下发生各种破坏状态的条件概率。其中以易损性曲线的形式来研究结构地震易损性是一种广泛适用的方法,其基本步骤如下:
(1)建立精细的结构非线性有限元模型;
(2)选择合适的地震动输入参数IM;
(3)确定结构的结构地震需求参数EDP;
(4)通过对每一个地震动-结构样本进行非线性时程计算,获取大量结构地震反应数据;
(5)对计算所得的结构地震反应数据进行分析,建立结构的地震需求模型GEDP(edp|im);
(6)定义结构的破坏状态,并建立相应每一破坏状态的结构承载力的概率密度函数;
(7)计算不同强度地震动作用下结构反应超过某一破坏状态所定义的结构承载能力的条件概率;
(8)绘制以所选地震动参数为自变量的结构地震易损性曲线。
2 结构计算模型
某钢筋混凝土(RC)框架结构为七层,抗震设防烈度为7度,II类场地。一层层高为4.5 m,其他层层高为3.6 m。框架的横向跨度分别为6.9 m、2.1 m、6.9 m。考虑基础的埋深,平面框架结构计算简图如图1所示。框架柱采用C35的混凝土、HRB435的纵筋以及HPB235的箍筋,柱截面尺寸500 mm×500 mm;框架梁采用C30的混凝土、HRB335的纵筋以及HPB235的箍筋。各个节点均按照规范进行了加固,以保证节点的刚度,边梁截面300 mm×600 mm,中间梁截面尺寸300 mm×500 mm。其中一层边柱、中柱底的截面配筋如图1所示。
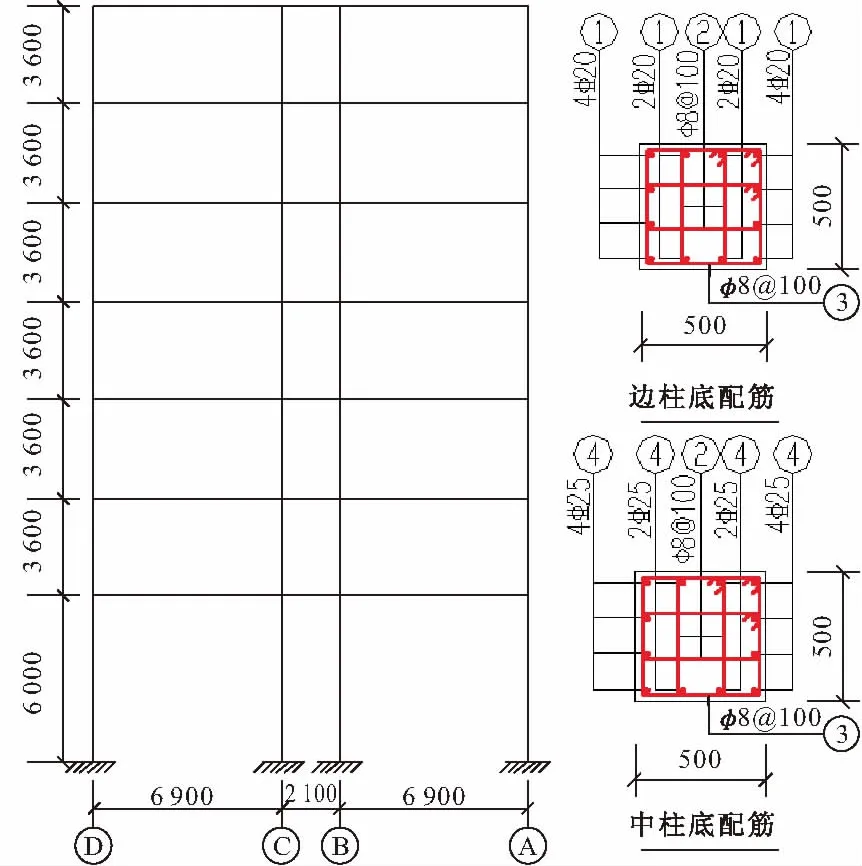
图1 RC框架结构计算简图
混凝土本构模型以美国Hognestad建议的模型为原型,如图2所示。钢筋的本构模型选取有明显流幅钢筋的应力-应变曲线为原型,把曲线分为几个折线段而成(如图3所示)。

图2 混凝土本构模型

图3 钢筋本构模型
采用有限元分析软件SAP2000建模,并对该结构进行非线性动力时程分析,其中梁、柱单元均采用框架单元来模拟,梁和柱两端的塑性角采用非线性Nlink单元来模拟,其中柱铰单元采用纤维PMM铰,梁铰单元设置弯矩铰。采用HHT法进行非线性运动方程求解。
3 RC框架结构地震易损性分析
3.1 破坏状态定义
在基于性能的抗震设计中,为了便于工程设计和评估,性态水准应该表达为各种性能指标。性能指标可用一个或多个性能参数来定义,本文选取位移指标来定义结构的破坏状态。
根据《建筑抗震设计规范》中规定[7]:钢筋混凝土框架结构层间位移角弹性极限为1/550,弹塑性极限为1/50;并参考文献[8]中的相关内容,定义RC框架结构破坏等级与变形的关系如表1所示。
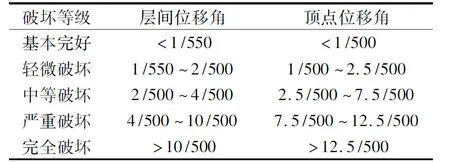
表1 结构破坏等级与位移角的对应关系
3.2 结构地震需求分析
云图法作为概率地震需求分析的一种常用方法,通过对确定性结构进行一系列地震动作用下的非线性动力反应分析,得到呈云状分布的反应结果,在IM和EDP的“云”上,采用统计回归技术,建立结构的概率地震需求模型。
选取地震动峰值加速度PGA(Peak Ground Acceleration, PGA)为地震动输入参数(Intensity Measure, IM),结构需求参数(Engineering Demand Parameter, EDP)选择最大层间位移角、最大顶点位移角。其中,结构的最大层间位移角(Inter-Story Displacement Angle, ISDA)为:
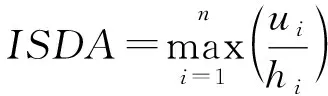
式中:ui为第i层的层间位移,hi为第i层的楼层高度,n为结构的总层数。
结构的顶点位移角定义(Roof Displacement Angle,RDA)为
(2)
式中:u为结构的顶点最大位移,H为结构总高度。
本文选取8条远场地震动记录,分别对地震动加速度峰值按照0.1g、0.2g、0.3g、0.4g、0.5g、0.6g和0.7g进行调整,共49种工况进行地震动输入。采用层间位移角、顶点位移角的自然对数作为结构在不同PGA下的地震需求,如图4和图5所示。在线性回归中,R2越接近1,在一定层度上表示该数据用线性方程表示的准确性越高。
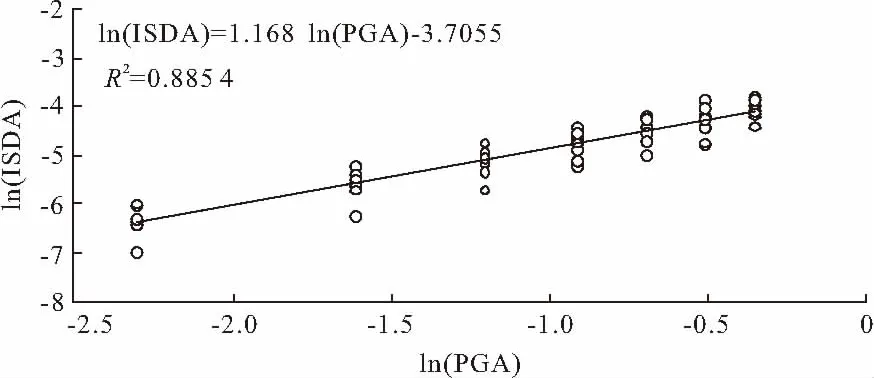
图4 最大层间位移角地震需求模型
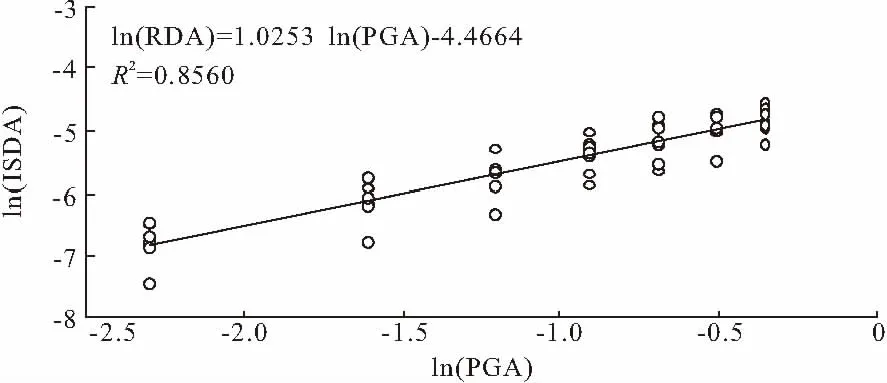
图5 顶点位移角地震需求模型
随着地震动强度的增加,结构一层柱下端塑性铰的变形越来越大。当PGA=0.1g时,塑性铰的塑性变形比较小(如图6);当PGA=0.3g时,塑性发展明显,存在着较大的残余变形,此时的极限弯矩为200 kN·m左右(如图7)。

图6 一层柱底塑性铰的弯矩-转角曲线(PGA=0.1g)
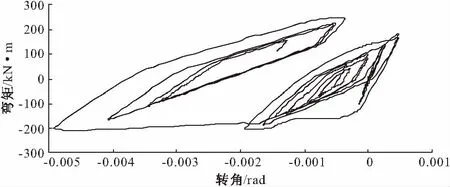
图7 一层柱底塑性铰的弯矩-转角曲线(PGA=0.3g)
3.3 易损性曲线的形成
假定在地震作用下结构最大顶点位移角和最大层间位移角均服从对数正态分布。此函数由结构需求对数均值μlnu和对数标准差σlnu来定义。
u=ln(μlnu,σlnu)
(7)
对计算得到的结果进行统计分析,得到对应不同PGA下的均值和变异系数,如表2所示。
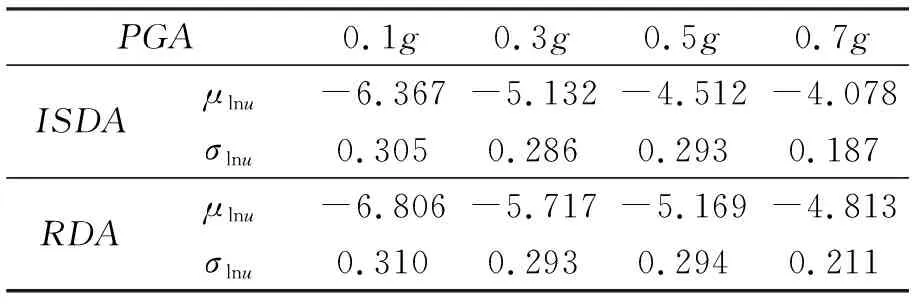
表2 结构需求统计信息
图8和图9给出了PGA=0.1g时,结构地震动需求的对数概率密度函数。由图可知,结构在PGA=0.1g地震动的作用下,保持基本完好的概率较高,在图8中结构保持基本完好的概率在50%左右,而在图9中结构保持基本完好的概率将近100%,这说明以ISDA作为地震动需求的量化指标所得到的结构破坏程度比以RDA作为地震动需求的量化指标的严重。

图8 以ISDA作为地震需求参数的概率密度函数(0.1g)

图9 以RDA作为地震需求参数的概率密度函数(0.1g)
图10和图11给出了PGA=0.3g时,结构地震动需求的对数概率密度函数。
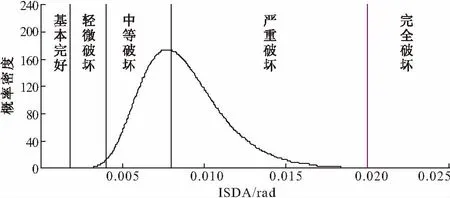
图10 以ISDA作为地震需求参数的概率密度函数(0.3g)
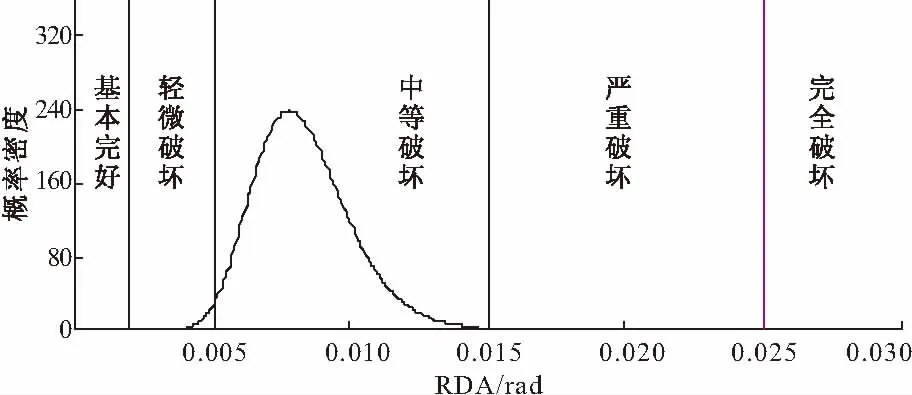
图11 以RDA作为地震需求参数的概率密度函数(0.3g)
结构的易损性曲线表示在不同强度地震作用下结构需求超过特定破坏状态的概率。根据本文对结构破坏等级的定义以及对结构地震动需求的概率分布的求解,可以由式(8)求得在不同ISDA下结构需求超过某一极限状态的概率。
(8)

以PGA=0.4g、ISDA为地震需求参数为例,计算轻微破坏的破坏等级的超越概率:
采用上述方法,可以得到以层间位移角ISDA和顶点位移角RDA为需求参数的结构地震动易损性曲线,如图12和图13。
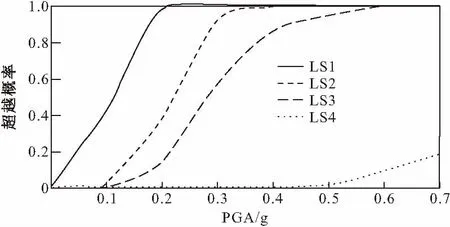
图12 以ISDA为需求参数的结构地震动易损性曲线
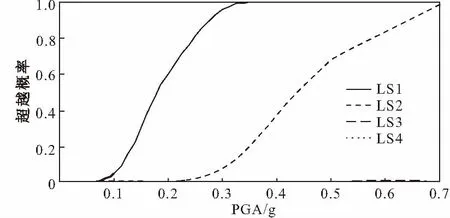
图13 以RDA为需求参数的结构地震动易损性曲线
对比图12和图13可知,采用不同的结构地震动需求参数对结构易损性曲线的影响非常大。在相同的PGA下,以RDA为参数的结构地震动易损性曲线表示结构破坏没以ISDA为参数的严重。考虑到以RDA为参数的结构地震动易损性曲线表示即使在PGA=0.4g地震动下,结构不会出现严重破坏这一明显与实际不相符合的情况,分析认为以RDA为参数的结构地震动易损性曲线是有较大的误差的。
4 结 论
(1) 选取最大层间位移角(ISDA)作为EDP得到的结构破坏程度比以最大顶点位移角(RDA)作为EDP的结果要严重。因此,为了较好地评价结构的抗震性能,寻求更为合理、可靠的需求指标尤为重要;另外,IM参数的选择也对结构的抗震性能影响也较大。
(2) 基于结构的地震易损性曲线,可以给出指定结构在地震作用下破坏概率,为结构地震灾害损失评估提供依据。
[1] 于晓辉, 吕大刚, 王光远. 土木工程结构地震易损性分析的研究进展[C]// 第二届结构工程新进展国际论坛,2008.
[2] H·Hwang,刘晶波.地震作用下钢筋混凝土桥梁结构易损性分析[J]. 土木工程学报,2004,37(6):47-51.
[3] 吕大刚, 于晓辉, 潘 峰. 基于改进云图法的结构概率地震需求分析[J]. 世界地震工程, 2010, 26(1): 7-15.
[4] 吴巧云,朱宏平,樊 剑. 基于性能的钢筋混凝土框架结构地震易损性分析[J]. 工程力学,2012, 29(9): 117-124.
[5] Schotanus M I J, Franchin P, Lupoi A, et al. Seismic fragility analysis of 3D structures[J]. Structural Safety, 2004, 26(4): 421-441.
[6] Sasani M, Kiureghian A D. Seismic fragility of RC structural walls: displacement approach[J]. Journal of Structural Engineering, 2001, 127(2): 219-228.
[7] GB 50011-2010, 建筑抗震设计规范[S].
[8] 刘晶波, 刘阳冰, 闫秋实,等. 基于性能的方钢管混凝土框架结构地震易损性分析[J]. 土木工程学报, 2010,43(2):39-47.
