某平面不规则结构基于两个软件弹塑性时程对比分析

郭昌漙, 吴晓涵, 李学平

(1.同济大学 结构工程与防灾研究所， 上海 200092；2.同济大学建筑设计研究院(集团)有限公司， 上海 200092)

1 工程概况

鸿运·金茂综合体为大型城市综合体项目，位于甘肃省兰州市城关区核心地段，庆阳路与平凉路交汇处。本项目一二期主要由2栋超高层建筑(A、B楼)以及商业裙楼组成，一期总建筑面积为28万m2。其中A塔楼(高塔)位于一期用地东南角，B塔楼(低塔)位于一期用地西北角。A、B塔楼与商业裙楼之间通过地上设抗震缝分开，形成3个独立的结构单体(A塔、B塔、裙楼)。综合体效果图见图1。

图1 综合体效果图

本文选取商业裙楼为研究对象，对其进行抗震性能研究。商业裙楼地下室共4层，B4至B1层层高分别为4.0 m、4.0m、6.2 m、7.0m，其中B2层部分设一夹层(层高3.1 m)，B1层为商业，其下各层为设备用房及汽车库，部分战时用作人防区域；地上共8层，业态以商业、娱乐、餐饮为主，屋顶部分用作设备用房。其中，一层层高6.0 m，上部各层层高5.4 m，结构总高度为43.80 m。

与A、B塔楼结构分开后的裙楼结构平面，南北向总长135.8 m，东西方向总宽134.4 m，呈不对称哑铃形平面。此外，由于南北贯通的通廊区域交通及商业需要，该区域楼板开洞较多，南北块的楼板联系相对被削弱(图2)。墙体位置多在角部，以增加结构抗扭性能。考虑到建筑空间的开敞性，针对主体结构超长，平面及荷载分布不规则等特点，且因防屈曲支撑(BRB)在地震作用下相比于普通斜撑能够提供稳定承载力，将结构部分剪力墙改为消能减震装置BRB构件，满足建筑功能要求，同时增加结构的安全性和可修复性。本工程六层以下竖向规整，但从六层屋面开始，裙楼屋顶逐层退进。结构平面图和裙楼屋顶平面图分别参见图2、3。

图2 裙楼一层平面图

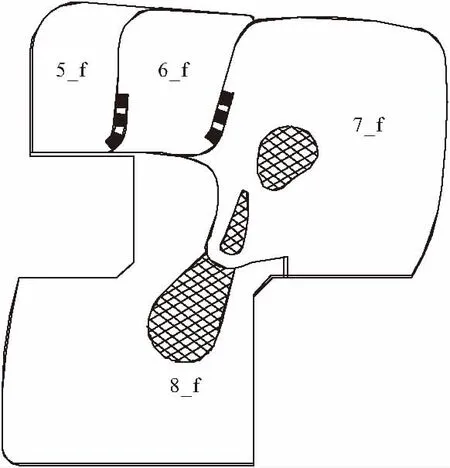
图3 裙楼屋顶平面图

根据GB 50011-2010《建筑抗震设计规范》的相关规定，该高层结构属于平面不规则结构。同时按照建质[2006]220号《超限高层建筑工程抗震设防专项审查技术要点》对该结构进行超限判定，结构属于超限高层建筑结构。结构的超限情况主要体现在扭转不规则，凹凸不规则，楼板不连续，尺寸突变和局部设有穿层柱、斜柱等五个方面。由于结构的不规则性及其建造环境于8度抗震设防区域，需对其进行罕遇地震下的弹塑性时程分析，考察其在八度地震下的损伤及变形情况。商业裙楼设计标准及基本参数见表1。

表1 裙楼设计参数

2 弹塑性分析模型和方法

2.1 NosaCAD构件有限元模型

本文中，框架梁、框架柱、支撑采用三段变刚度杆单元模型，由位于中部的线弹性区段和位于杆两端的弹塑性段组成[1]。梁单元只发生弯曲破坏，其受弯弹塑性变形集中在杆端附近的局部区域，塑性铰只在杆件两端出现，因此梁单元可以简化为由两类区域组成的三段变刚度杆单元模型[2]：位于中部的线弹性区域和位于两端的定长弹塑性区域。混凝土框架梁单元截面的弹塑性段弯矩-曲率骨架曲线采用三折线模型[3，4]，三折线模型滞回曲线如图4所示。由于框架柱承受双向弯矩和轴力共同作用，框架柱单元采用纤维模型，纤维模型中的混凝土本构考虑受拉应力，梁、柱混凝土构件以边缘混凝土达到极限压应变为破坏条件，如图5所示。钢和钢筋纤维采用理想弹塑性的二折线模型，并考虑屈服强化，屈服后的弹性模量取初始值的1%。剪力墙的暗柱在采用NosaCAD建立模型时，已作为柱单元建立在剪力墙边缘，和剪力墙相互作用。

图4 NosaCAD三折线弯矩-曲率滞回模型

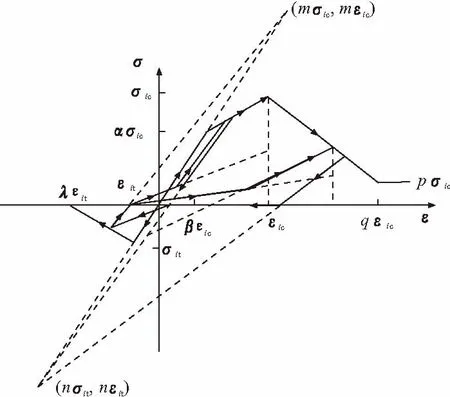
图5 NosaCAD混凝土本构模型-曲率模型

剪力墙体采用平板壳精细有限元模型，平板壳单元由平面应力单元(膜单元)和板单元组合而成。壳单元考虑面内非线性，面外弹性。壳单元中的膜单元带有旋转自由度[5]，可以方便地与梁进行连接。墙体单元中的钢筋分布采用弥散模式，在壳元表面两个受力方向上按配筋率均匀分布。钢筋的本构模型采用理想弹塑性模型。混凝土本构模型采用单轴等效应力-应变关系模型[6，7](Darwin-Pecknold模型)，单轴等效应力-应变关系滞回曲线与纤维模型中的混凝土本构模型相同，但考虑正交方向上应力状态对强度的影响。

结构中的防屈曲支撑(BRB)构件，采用两端铰接的桁架单元进行模拟，桁架单元中的钢材纤维采用理想弹塑性的二折线模型，考虑了对称的单轴拉压本构关系。为充分模拟到其进入塑性状态的变形，假定整根杆件都为弹塑性区域。

因为结构为典型的平面不规则结构，所以在NosaCAD中结构楼板采用弹性板单元进行模拟。

2.2 Perform-3D构件有限元模型

Perform-3D中非线性杆单元模型采用与NosaCAD类似的三段变刚度杆，如图6所示。弹塑性区段受力-变形关系采用弯矩-曲率模型或纤维模型。Perform-3D中未直接建立剪力墙边缘暗柱，采用对剪力墙边缘纤维进行相应放大以模拟暗柱的影响。Perform-3D中采用宏观分层单元来模拟剪力墙构件。本文采用General wall单元模拟剪力墙构件。General wall单元通过宏观分层模型模拟剪力墙的弯曲、剪切、斜向受压等力学特性。剪力墙的剪切特性是通过定义其剪切强度来实现的，本文的剪切特性是通过定义混凝土材料的剪切强度来实现的[8]。由于Perform-3D墙单元的结点不具备旋转自由度，故梁与墙体的连接需采用施加内嵌梁的方式连接(图7)。Perform-3D中采用专门的防屈曲支撑(BRB)单元来模拟防屈曲支撑(BRB)构件。本文结构模型杆件数目较多，当结构模型因为平面不规则采用弹性楼板时，计算速度偏慢，无法收敛，为了提高计算效率，本文结构采用局部刚性楼板假定，在结构的连接削弱处采用弹性楼板，其余部位采用刚性楼板假定进行模拟(图2)。

图7 剪力墙内置内嵌梁

图6 Perform-3D非线性杆件模型

2.3整体结构的计算模型

Perform-3D、NosaCAD分别建立空间分析模型(图8),并采用以下相同的基本假定：(1)模型不包括地下室，地面作为结构嵌固端；(2)按照100%恒载、100%附加恒载和50%活载作为模型计算质量，Perform-3D模型计算质量为146980 t，NosaCAD模型计算质量为147623 t，两者十分接近。

图8 整体模型

3 结构自振特性和地震波的选取

3.1 结构自振特性

在时程分析之前先进行振型分析，从而可以对结构的基本动力特性作初步判断，并能验证模型的正确性。表2列出了NosaCAD和Perform-3D的前三阶振型，并给出相应周期的振型(图9)。

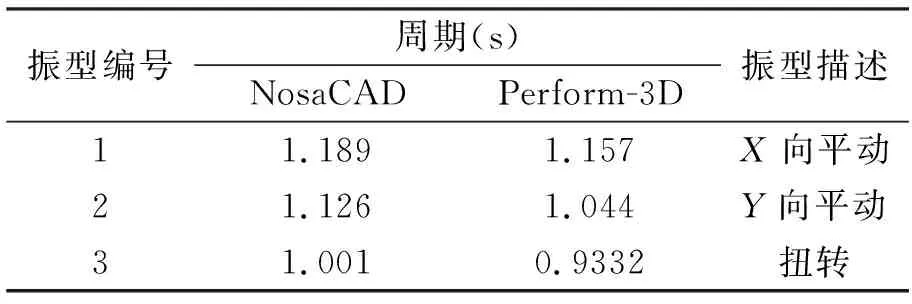
表2 结构自振特性

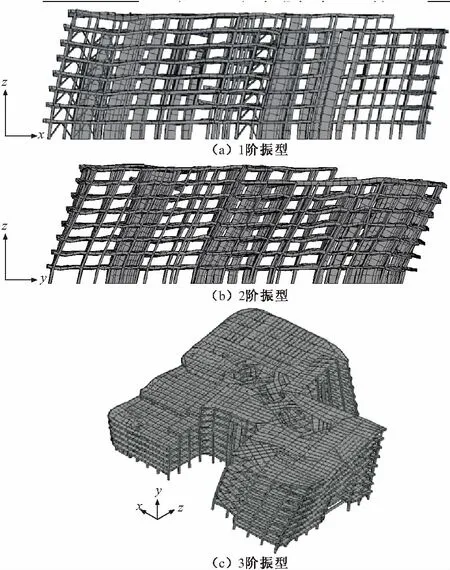
图9 NosaCAD结构前三阶振型

由以上表格数据对比及振型图结果可以看出：前三阶周期NosaCAD与Perform-3D吻合较好，NosaCAD略高；两软件结构模型的振型出现顺序相同，各模型质量相差极小，说明各模型的结构刚度分布和质量大小基本一致。

3.2 地震波选取

本文采用的地震波来自SATWE，根据抗震规范要求，按照结构所处场地的特征周期选取了两条天然波和一条人工波对该结构进行弹塑性时程分析，取其反应的包络值作为结构的抗震性能评价依据，其中两组天然地震波LN1和LN2，一条人工模拟地震波LA。模态计算结果表明，结构的X向整体刚度小于Y向整体刚度。把结构的X方向定为结构的主方向，Y方向定为结构的次方向，三条地震波均采用双向输入，将地震波的主方向时程记录按结构的主方向进行输入。选取的地震波加速度时程记录如图10所示。

图10 输入地震波记录(x、y向)

主次方向地震波的峰值按1∶0.85取值。加速度峰值按《建筑抗震设计规范》规定取值，在8度罕遇地震作用下，取4000 mm/s2。参考结构第一自振周期，确定地震波持续时间为30 s。动力方程的阻尼采用瑞利阻尼，结构考虑为框架剪力墙结构，阻尼比取为5%。采用Newmark-β法进行时程计算，γ值取为0.50，β值取为0.25。

4 时程分析结果

4.1 两个软件位移时程及位移角对比

分析结果显示该结构在各条地震波作用下均存在扭转效应，同时考虑到结构扭转位移比较大，楼板存在大开洞，连接薄弱，具有较大的面内变形，故取图2平面上N1、N2、N3、N4、N5作为层间位移角的考察位置。

由于本结构为不规则结构，并且其建造地区为8度抗震设防区域，所以结构的地震响应较为强烈。结构在相同加速度峰值的不同地震波作用下反应相差较大。

罕遇地震下，对比三条地震波的时程分析结果。可以得到LA波输入的地震响应相比LN1波、LN2波的更为剧烈。最大层间位移角出现在N5结点串顶层，NosaCAD中的值为1/132，Perform-3D中其值为1/141。分析结果表明，结构主要竖向构件的最大层间位移角都满足1/100的规范限值要求。

图11、12为两个软件分别计算所得8度罕遇LN1、LN2波地震作用下N1(5层)结点的位移时程曲线。可以看出，两软件的模型在不同地震波作用下相同结点位移时程数值有所差别，时程曲线走势一致，计算结果吻合较好。

图11 8度罕遇LN1波地震作用N1(5层)结点位移时程对比

图12 8度罕遇LN2波地震作用N1(5层)结点位移时程对比

图13 8度罕遇LA波地震作用下N1的层间位移角包络图

图13、14给出了8度罕遇LA波输入下两软件的模型中个别观察点的层间位移角包络图。在LA波作用下，对比两个软件分别计算得到的结构N1和N5结点串X、Y向层间位移角包络图，可以发现，两个软件下的N1层间位移角包络图走势相同，N5层间位移角包络图变化趋势基本一致。在图13中，远离楼层刚度中心的N1结点串在Perform-3D模型中计算得到的包络值基本大于NosaCAD，说明Perform-3D中N1结点串由于局部弹性楼板，分块刚性楼板的影响，结构中的刚性楼板区域都为强连接，结点串上的5个结点绕着刚性楼板的刚度中心作统一转动，转动幅度大于因设定全弹性楼板而出现较多连接削弱部位的NosaCAD模型中N1层间位移角包络值。对比两软件下靠近楼板削弱位置的N5结点串X、Y向的层间位移角包络图，NosaCAD的值总体上不再小于Perform-3D,说明由于结点串位置的变化，在离楼层刚度中心较近的区域，局部弹性楼板，分块刚性楼板的模型的层间位移角包络值受刚性楼板影响较小，能够较接近于全弹性楼板假定下计算得出的值。

图14 8度罕遇LA波地震作用下N5的层间位移角包络图

4.2 结构损坏情况分析

NosaCAD模型和Perform-3D中，结构破坏的顺序以及程度基本相同。在8度罕遇地震作用下，由LA波引起的结构破坏最为严重，图15、16分别给出了两个软件中结构在LA波沿着结构x方向为主方向输入时结构的破坏情况。

对比以上两软件结构损坏图可以看出：

(1)两软件中结构的梁基本进入到非线性状态，大部分的连梁被压碎，降低了结构的刚度，减小了地震作用。

(2)在NosaCAD中可以观察到多数剪力墙出现开裂。两软件中都有小部分柱子出现塑性铰，其中Perform-3D出现塑性铰的柱子较少，位于首层和第七层边缘的个别柱子出现局部压碎。对比NosaCAD和Perform-3D柱子的损伤情况，NosaCAD出铰的柱子一部分和Perform-3D的相对应，另一部分为剪力墙的边缘暗柱。

图15 8度罕遇LA波地震作用结构损坏(NosaCAD模型)

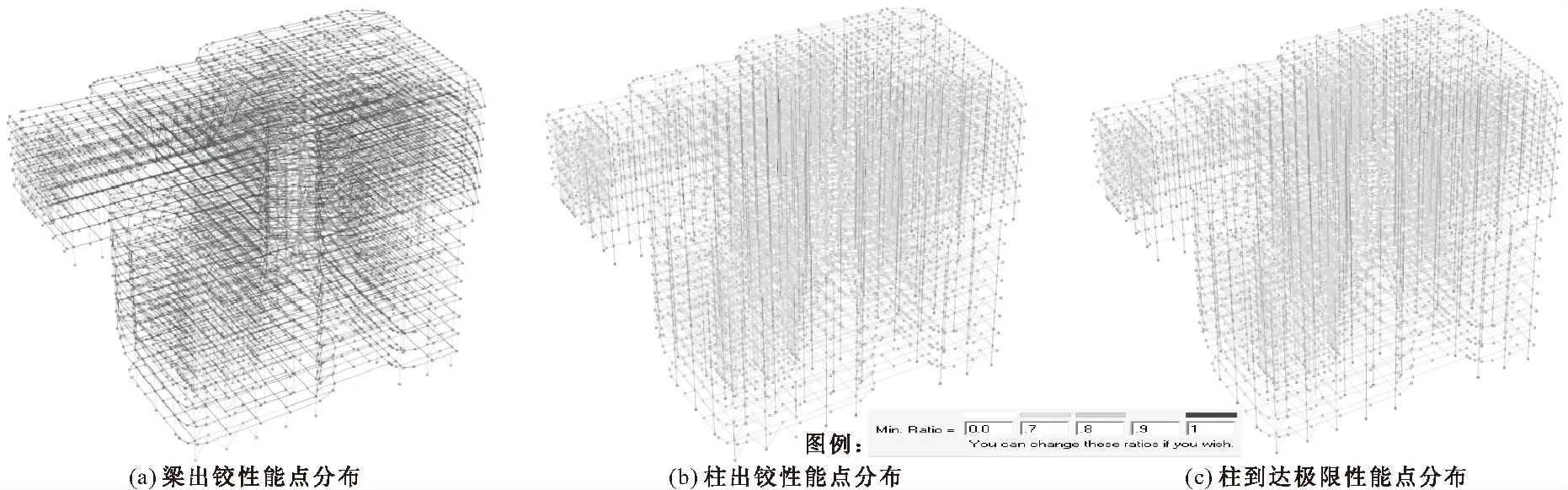
图16 8度罕遇LA波地震作用结构损坏(Perform-3D模型)

(3)在NosaCAD中，防屈曲约束支撑(BRB)都未屈服，保持着弹性阶段的刚度和工作状态。在Perform-3D中，第二层的防屈曲约束支撑部分进入到了屈服状态,说明NosaCAD与Perform-3D中杆件的轴力存在着一定的差异，通过对比防屈曲约束支撑(BRB)耗能在结构总的非线性耗能中所占比例，该比例不到1%，BRB对结构非线性耗能几乎没有影响，在Perform-3D中所起的作用与NosaCAD近似，主要是为了提供稳定的承载力和刚度。

(4)从两个软件的破坏顺序来看，结构的破坏首先都发生在剪力墙连梁上，随后部分主梁出现塑性铰，之后柱子钢筋屈服，最后发生个别柱子底部混凝土的压碎破坏。设计满足了“强墙肢弱连梁”、“强柱弱梁”的原则，在罕遇地震作用下作为抗震第一道防线的连梁首先发生屈服破坏，耗散了一定的能量，避免或减小了剪力墙的破坏，结构整体能满足大震不倒的要求。

5 结 论

(1)Perform-3D、NosaCAD两个程序计算得到的自振周期和振型吻合较好。

(2)对比两个软件的计算结果，NosaCAD和Perform-3D所得结构的动力响应基本相同，结构损伤情况基本一致。

(3)两个软件中结构在8度罕遇地震作用下,结构变形满足层间位移角限值要求，总体上塑性铰首先出现于上部楼层结构的剪力墙连梁位置处，随后框架梁出现损坏，结构构件的损坏顺序说明结构符合“强墙肢弱连梁”、“强柱弱梁”的设计要求，并且有利于结构合理地耗散地震波输入能量，整体结构能满足“大震不倒”的抗震设防要求。

(4)结构在所选3条波的八度罕遇地震作用下，NosaCAD中的防屈曲约束支撑(BRB)都未屈服，保持着弹性阶段的刚度。Perform-3D中的防屈曲约束支撑(BRB)个别进入到了屈服状态，说明两个软件得到的杆件内力存在着一定差异。对比防屈曲约束支撑(BRB)耗能在结构总的非线性耗能所占比例，BRB对结构非线性耗能几乎没有影响，防屈曲约束支撑的主要功能是为了代替剪力墙，提供稳定的承载力和刚度。

[1] 孙方涛，吴晓涵，吕西林．竖向地震作用下某大跨悬挑结构反应分析[J]．结构工程师，2009，25(4)：71-77．

[2] 顾祥林，孙飞飞．混凝土结构的计算机仿真[M]．上海：同济大学出版社，2002．

[3] 吕西林．复杂高层建筑结构抗震理论与应用[M]．北京：北京科学出版社，2007．

[4] 吕西林，金国芳，吴晓涵．钢筋混凝土结构非线性有限元理论与应用[M]．上海：同济大学出版社,2002．

[5] 龙志飞，岑 松．有限元法新论：原理·程序·进展[M]．北京：中国水利水电出版社，2001．

[6] 吴晓涵，吕西林．反复荷载下混凝土剪力墙非线性有限元分析[J]．同济大学学报，1996，24(2)：117-123．

[7] Darwin D, Pecknold D A. Analysis of RC shear panels under cyclic loading[J]. Journal of the Structural Division,1976,102(2):355-369．

[8] 曾 明，刘博文. PERFORM-3D基本操作和原理[M]. 北京：北京工业大学，2012.