铰接点纵向间距对铰接跨破坏状态的影响分析

孙全胜， 吴 桐， Walter Yang， Reginald DesRoches

(1.东北林业大学 土木工程学院， 黑龙江 哈尔滨 150040；2.佐治亚理工学院 土木与环境工程学院， 美国 亚特兰大 30332)

加利福尼亚洲位于美国西南部，属于环太平洋地震带，是地震频发地区。Yuba桥是加利福尼亚洲的一座8跨预应力混凝土连续曲线箱梁桥，该桥梁设计采用墩梁固结形式，并在其中两跨设置铰连接以减少结构的自由度。铰接两侧梁段的纵向间隙采用刚度较小的聚苯乙烯进行填充。当地震发生时，地震力往往会使铰接两侧梁段发生纵向和横向的碰撞，碰撞力会造成铰接位置发生局部破坏；或者增加梁跨支点的弯矩，造成梁跨根部的塑性破坏。不同的纵向间隙对结构碰撞的状态和时刻有较大的影响，同时也影响了铰接构造内的各构件的非线性变化过程及主梁的塑性破坏状态，在地震响应分析过程中不可忽略。本文应用地震工程模拟系统OpenSees[1]对Yuba桥铰接梁跨进行Pushover分析，研究纵向的间距设置对铰接梁跨破坏状态的影响。

Yuba桥为上部结构48.77 m+64.01 m+4×79.25 m + 64.01 m + 48.77 m的预应力混凝土连续曲线梁桥，曲线半径为914.4 m，圆心角为34°，如图1所示(只示出桥梁1～4跨，5～8跨与其对称)，全桥为变截面形式，由支点截面通过抛物线过渡到跨中截面。桥墩直径3.05 m,与主梁固结。为了减少结构自由度，在第3跨和第6跨反弯点处设有铰接构造。铰接构造如图2～4所示，铰连接设为上下及左右咬合形式，纵向通过28根直径为31.75 mm限位钢束限制纵向位移；横向设置4个受压橡胶支撑垫限制横向的相对位移，阻止结构横向碰撞；竖向设有2个橡胶支座，即可以限制竖向相对位移，又可以为横向提供剪切刚度，阻止横向碰撞。铰接点之间的间隙均为76.2 mm，间隙处使用聚苯乙烯填充。

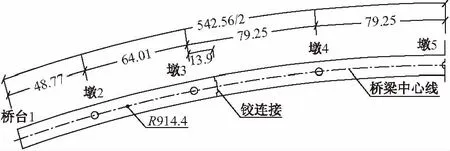
图1 结构平面布置/m

图2 铰接跨平面/m

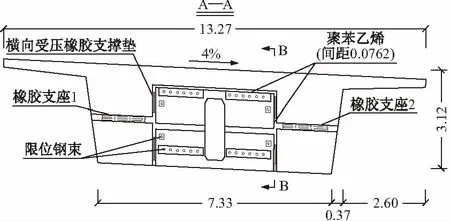
图3 铰接位置横截面/m

图4 铰接位置立面/m

1 结构建模

1.1 纤维单元模型

为了准确的探究铰接位置的破坏状态，本文采用OpenSees中的Displacement-Based Beam- Column Element(纤维梁柱单元)进行建模[2]，如图5所示。纤维单元模型能将结构划分成很多细小的纤维，通过定义材料属性赋予结构纤维的本构关系。在有限元计算过程中，纤维单元模型假定构件的截面在变形过程中始终保持为平面，通过计算构件截面的弯曲应变和轴向应变来计算每一个细小纤维的应变，从而得到截面刚度[3]。

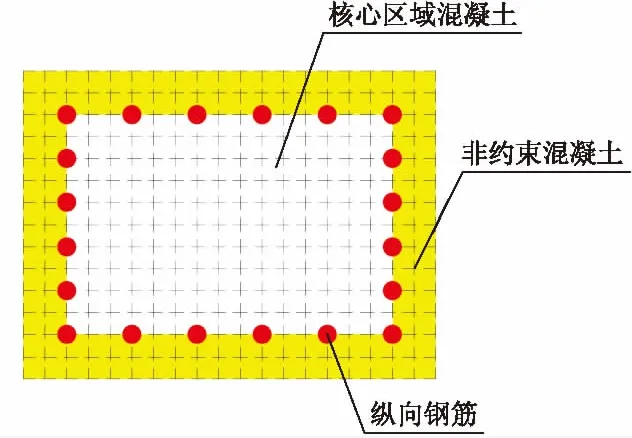
图5 钢筋混凝土纤维单元

1.2 材料本构模型

1.2.1混凝土本构关系

主梁的混凝土材料使用OpenSees中Concrete01材料进行模拟，该混凝土材料使用Kent-Scott-Park模型[4]，如图6所示，忽略混凝土的受拉过程。此模型由上升段的二次抛物线及下降段的折线组成。上升段采用Hognestad建议的二次式y=-x2+2x,下降段的斜线是由σc=0.5fc应力处的应变确定[1,5]：

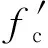
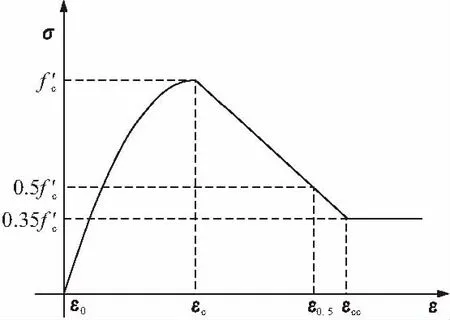
图6 Kent-Park混凝土模型

1.2.2钢筋的本构关系

钢筋的本构关系采用Giuffré-Menegotto-Pinto模型[1]，不考虑钢筋硬化，如图7所示。

图7 Giuffré-Menegotto-Pinto 钢筋模型

1.3 碰撞单元模拟

碰撞单元采用Muthukumar[6]及Nielson[7]提出的双线性曲线模型，使用ElasticPPGap材料进行模拟，如图8所示。其中：Gap为碰撞间距；Kt1=586.3 (kN/mm)/m；Kt2=201.73 (kN/mm)/m；Keff=238.5 (kN/mm)/m,δy=2.54 mm；δm=25.4 mm。

图8 碰撞模型

1.4 橡胶支撑垫、橡胶支座及限位钢束的模拟

横向受压橡胶支撑垫，橡胶支座及限位钢束采用Steel01材料进行模拟[8]，如图9所示。当材料达到屈服极限后，其刚度快速降低。

图9 橡胶支撑垫、橡胶支座及限位钢束模型

1.5 有限元建模

首先进行结构的整体建模，将各跨主梁和桥墩全部建立出来，并在铰接点位置施加径向力，进行Pushover分析。发现整体模型无法将铰接位置的局部破坏状态体现出来，而且铰接构造内也很难发生横纵向的碰撞。这是因为主梁和墩柱均会参与分担Pushover过程中的径向力，故铰接构造的破坏状态无法被放大。

为了探究铰接跨的破坏形式，选取铰接梁跨(第3跨)建立单跨模型。忽略桥墩的影响，考虑结构的墩梁固结形式，选择将单跨模型两侧边界条件设为全部固结。因结构曲线半径较大，单跨跨径较小，故将单跨主梁近似为直线结构。铰接构造的实际纵向间距为76.2 mm，如图2、4所示。为了校验模型准确性，建立细化模型和简化模型，细化模型为将铰接位置的咬合构造全部建立出来，通过Zerolength单元模拟各位置的刚度、碰撞和屈服状态，如图10(a)所示；简化模型为只在铰接点两侧各设置一个节点，在节点间通过多个Zerolength单元模拟铰接点的横向、竖向及纵向的刚度、碰撞和屈服状态，如图10(b)所示。模型建立完成后，对两个模型分别进行Pushover分析，在铰接点右侧施加Pushover横向力，并对铰接点横向位移进行控制，控制间隔为12.7 mm，记录横向力大小和铰接点的横向位移[9,10]。细化模型和简化模型的Pushover对比结果如图11所示。

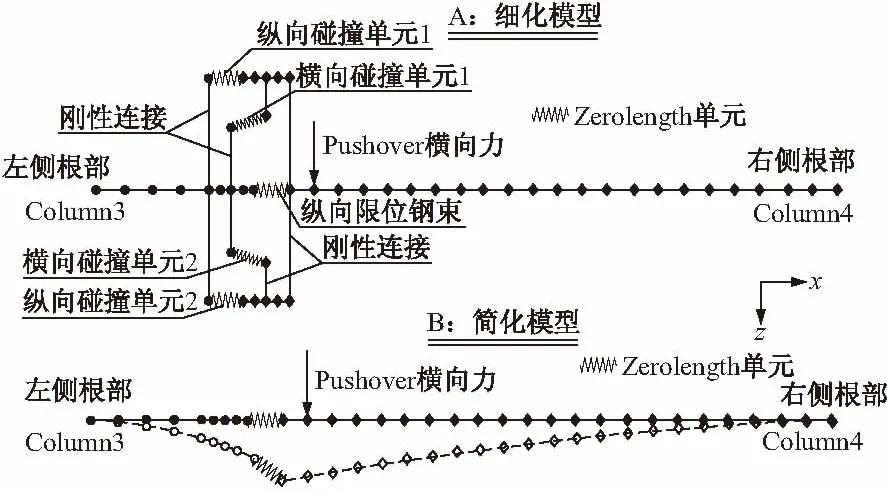
图10 OpenSees有限元模型

如图11所示，两种模拟方法在横向位移达到241.3 mm之前，数值趋势一致，曲线重合，但是当横向位移超过241.3 mm时，两条曲线不再重合。这是由于细化模型对铰接构造的划分更接近实际，当横向位移为241.3 mm时细化模型发生纵向碰撞，而简化模型的纵向碰撞要相对滞后，这就造成后期Pushover曲线的不重合。

图11 细化模型和简化模型对比

为了研究纵向间距对铰接梁跨破坏状态的影响，选用细化模型进行研究。另取纵向间距为63.5 mm、88.9 mm及更小的12.7 mm进行对比分析，Pushover加载位置及控制位移增量同上。

2 Pushover对比分析

2.1 Pushover横向力对比

分别对纵向间距为12.7 mm、63.5 mm、76.2 mm、 88.9 mm 的模型进行Pushover分析，记录铰接位置横向力随横向位移的变化，如图12。如图所示，结构的第一次屈服过程随着碰撞间距的减小而缩短。当纵向间距为12.7 mm时，甚至没有出现第一次屈服过程。

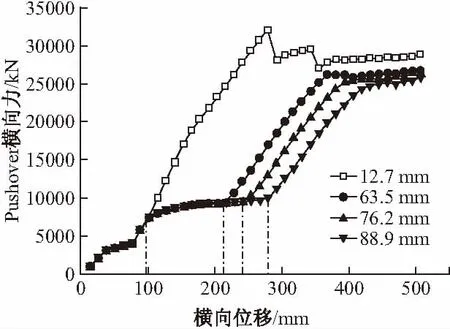
图12 不同纵向间距模型的对比

2.2 横向受压橡胶支撑垫

图13为不同纵向间距的模型横向受压橡胶支撑垫压力随铰接位置横向位移变化图。图中可见，横向受压橡胶支撑垫不受纵向间距的影响，当铰接位置的横向位移达到43.18 mm的时候，受压橡胶支撑垫开始发生屈服。

图13 横向受压橡胶支撑垫压力对比

2.3 受剪切橡胶支座

图14、15为不同纵向间距的模型橡胶支座横向剪力及纵向剪力随铰接位置横向位移变化图。

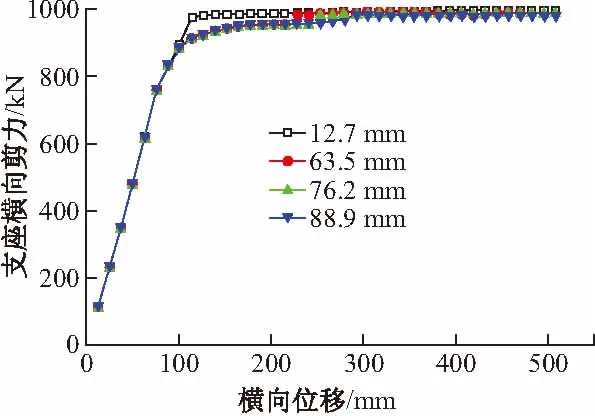
图14 橡胶支座横向剪力对比

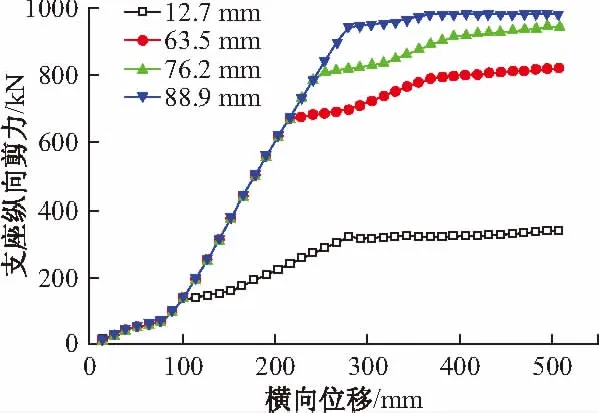
图15 橡胶支座纵向剪力对比

由图可知，纵向间距对支座的横向剪力影响很小，对纵向剪力影响较大。较小纵向间距能降低橡胶支座在纵向的位移，有利于延长橡胶支座的纵向弹性工作阶段。

2.4 纵向限位钢束

图16为不同纵向间距的模型纵向限位钢束内力随铰接位置横向位移变化图，可见，纵向限位钢束的屈服时刻不受纵向间距的影响。

图16 纵向限位钢束内力对比

2.5 纵向碰撞单元

图17为不同纵向间距的模型纵向碰撞单元1的碰撞力随铰接位置横向位移变化图(纵向碰撞单元2未发生碰撞，故未列出)，可知，纵向间距为12.7 mm、63.5 mm 、76.2 mm、88.9 mm的模型的碰撞时刻分别发生在铰接位置横向位移为93.98 mm、228.6 mm 、241.3 mm、271.78 mm。

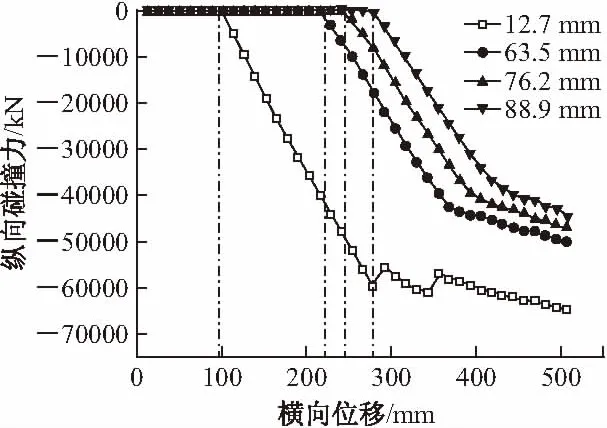
图17 纵向碰撞力对比

2.6 横向碰撞单元

图18为不同纵向间距的模型横向碰撞单元1的碰撞力随铰接位置横向位移变化图(在Pushover过程中，并未发生横向碰撞单元2的碰撞)。

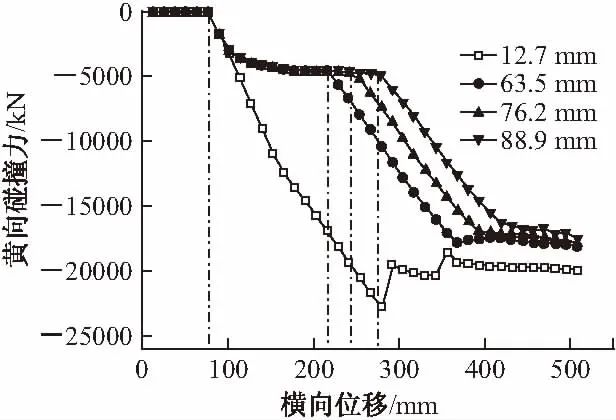
图18 横向碰撞力对比

(1)当横向碰撞力小于0时，结构发生横向碰撞，图18中所有模型的横向的碰撞发生在横向位移81.28 mm处，可见纵向间距的改变并不会影响横向碰撞单元的碰撞时刻。当横向位移达到81.28 mm时，左侧主梁的根部发生塑性破坏(如图19所示)，这使在横向发生碰撞后横向碰撞力与铰接处横向位移的曲线处于屈服状态，即横向位移增大但碰撞力却不增大。

(2)图18中各个曲线的第二个折点分别对应图17中纵向碰撞单元的碰撞时刻(12.7 mm模型横向碰撞和纵向碰撞几乎在同一时刻发生，故图18对其显示不明显)，这说明纵向碰撞力的产生会增加左侧主梁根部的弯曲刚度，会结束这种位移增大、碰撞力不增大的现象，仿佛使主梁结构从塑性状态重新回到了弹性状态，图12的曲线趋势也印证了这一点。

2.7 梁跨根部弯矩与曲率比

采用弯矩与曲率之比代表结构的刚度情况，图19、图20分别为铰接跨左侧、右侧梁段根部弯矩与曲率的比值随铰接位置横向位移变化图。

图19 左侧根部弯矩曲率的比值对比

图20 右侧根部弯矩曲率比值对比

如图19，铰接位置的横向位移为81.28 mm时，左侧梁段根部的弯矩与曲率的比值均发生下降趋势，这是因为左侧梁段的根部已经产生了塑性破坏。可见不同的纵向间距并不能改变左侧梁段屈服时所对应的位移，但是较小的纵向间距能够抑制左侧梁段刚度减小的速率。

由2.5节可知，纵向间距为12.7 mm、63.5 mm、76.2 mm、88.9 mm的模型分别在横向位移93.98 mm，228.6 mm，241.3 mm，271.78 mm时发生纵向碰撞。如图20，在以上位移点，各个模型的右侧梁段根部的弯矩和曲率比值均开始增大，说明当纵向碰撞发生时，结构受到轴向压力作用，这使结构的刚度发生增大现象，即弯矩和曲率的比值相应增大，纵向碰撞发生的越早，结构的刚度增长的越早。最终弯矩与曲率的比值都发生急剧下降，说明主梁的右侧根部发生了塑性破坏，这与图12中的各曲线的第二次屈服相对应。

2.8 不同纵向间距对计算结果的影响分析

横向受压橡胶支撑垫、橡胶支座的横向剪力、纵向限位钢束的破坏结果都是受铰接点横向位移控制的，且Pushover每级的横向位移控制间隔不变，故不同的纵向间距对以上三项的结果影响较小。橡胶支座的纵向剪力、铰接点纵向碰撞过程、铰接点横向碰撞过程、主梁根部的弯矩曲率都是跟纵向碰撞密切相关的，纵向间距决定了纵向碰撞的时刻，故不同的间距对以上几项产生不同的计算结果。

3 结 论

(1)在对桥梁铰连接进行模拟时，如果结构在计算过程中并未发生纵向碰撞，简化模型和细化模型均可被采用。如果结构发生纵向碰撞，细化模型对纵向碰撞的模拟更为准确。

(2)铰接点的纵向间距对结构的纵向碰撞、横向碰撞以及橡胶支撑垫、剪切支座的破坏过程、主梁的屈服破坏过程都有很大的影响。较小的碰撞间距会让结构在横向地震位移很小时就发生纵向的碰撞，这样能延长橡胶支座在纵向的弹性工作阶段。

(3)当纵向碰撞发生时，墩梁固结处主梁的弯矩与曲率的比值增大。弯矩代表结构承担的弯曲内力，而曲率代表了结构的弯曲变形情况。弯矩与曲率的比值增大说明在纵向碰撞发生时，墩梁固结处主梁在弯曲变形相同的情况下可以承担更大的弯曲内力。纵向间距越小，纵向碰撞发生的越早，这就更能延长固结处主梁的线性工作状态。当主梁固结处发生塑性破坏时，较早的纵向碰撞还能抑制主梁刚度下降的速率。

[1] McKenna F, Fenves G L. The OpenSees Command Language Primer [R].Berkeley: PEER,University of California,2000.

[2] Fabio F T, Enrico S, Filip C F. A Fiber Beam-Column Element for Seismic Response Analysis of Reinforced Concrete Structures,EERC Report No.91/17[R]. California: College of Engineering, University of California Berkeley,1991.

[3] 朱雁茹,郭子雄.基于OpenSEES的SRC柱低周往复加载数值模拟[J].广西大学学报,2010,35(4):555-559.

[4] Kent D C, Park R. Flexural members with confined concrete[J]. Journal of the Structural Division, 1971, 97(7): 1969-1990.

[5] 王 瑾,蔡新江,田石柱.基于OpenSees的CFRP加固RC短柱抗震性能数值模拟[J].世界地震工程, 2009, 25(4): 108-111.

[6] Muthukumar S.A Contact Element Approach with Hysteresis Damping for the Analysis and Design of Pounding in Bridges [D].Atlanta: School of Civil and Environmental Engineering, Georgia Institute of Technology,2003.

[7] Nielson B G.Analytical Fragility Curves for Highway Bridges in Moderate Seismic Zones[D]. Atlanta: School of Civil and Environmental Engineering, Georgia Institute of Technology, 2005.

[8] Karthik N R. Next Generation Seismic Fragility Curves for California Bridges Incorporating the Evolution in Seismic Design Philosophy[D].Atlanta: School of Civil and Environmental Engineering, Georgia Institute of Technology, 2012.

[9] 林树枝,袁兴仁,黄建南,等.基于Pushover的中小学框架校舍抗震性能研究[J].土木工程与管理学报, 2011, 28(3):259-263.

[10]韩小雷,陈学伟,戴金华,等.基于OpenSEES的剪力墙低周往复试验的数值分析[J].华南理工大学学报(自然科学版),2008,36(12):7-12.