微细电火花线切割与超精磨削加工表面摩擦性能比较

崔海 ，郭黎滨，张彬，陆喜文

(1. 哈尔滨工程大学 工程训练中心，黑龙江 哈尔滨，150001；2. 哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨，150001)

随着微机电系统的深入发展和广泛应用，微细电火花线切割加工技术(MWEDM)越来越受到人们的重视[1]。MWEDM以其较高的加工精度、加工效率和性价比用来加工微小复杂的三维零件，已经成为微细加工领域重要的加工方法[2]。零件表面的微观形貌在很大程度上影响着零件的摩擦磨损性能。由于MWEDM表面是由电极丝往复运动过程中与工件之间的微能量(小于35 μJ)随机放电形成的，其形成机理与切削加工方法差别较大，所以，其微观形貌特征有其固有的特点。润滑是降低摩擦副的摩擦阻力并减少材料磨损的主要措施[3]。国内外对MWEDM的研究主要集中在加工设备的研制和工艺参数的优化方面，对MWEDM加工表面所特有的微观形貌研究较少，尤其是针对MWEDM 表面质量和摩擦性能的应用基础研究尚未全面开展。因此，掌握 MWEDM 表面的摩擦磨损特性对提高零件的使用寿命和可靠性具有重要的指导意义。本文作者结合 MWEDM 表面的微观形貌特征，对 MWEDM 表面在润滑条件下进行摩擦磨损实验研究，以探索 MWEDM 表面形貌与摩擦磨损行为之间的关系，并与超精磨削加工表面的摩擦磨损性能进行比较，进一步推动MWEDM技术的研究和应用。

1 实验方法

1.1 试样制备

试件材料为 W18Cr4V高速工具钢，材料经热处理后洛氏硬度为 63。选用哈尔滨工业大学研制的HIT100 型微细电火花线切割机床加工，油基工作液，电极丝为直径30 µm的钨丝，走丝系统为往复双向走丝，电源采用 RC脉冲电源。试件的长×宽×厚为1 mm×1 mm×1.5 mm。由于MWEDM表面的微观三维形貌与加工过程中的放电脉冲能量有关。因此，选择6种不同的放电脉冲能量，比较其加工表面的摩擦磨损性能，如表1所示。

表1 微细电火花加工放电脉冲能量方案Table 1 Discharge pulse energy program of MWEDM

1.2 实验设备及检测

采用自行研制的摩擦试验机和配套的测试系统进行实验，上试件为微细1～6号试件和材料及热处理状态相同超精磨削加工试件(表面粗糙度Ra=0.4)，摩擦副下试件为超精磨削加工(Ra=0.2)试件。摩擦试验机利用曲柄连杆机构，带动下试件在精密直线滑轨上与固定在夹紧块上静止的上试件做往复滑动，试件之间为面接触，往复行程为80 mm。试验机具体结构如图1所示。

润滑油选择黏度适中且氧化安定性、化学稳定性和光安定性能出色的缝纫机油，运动黏度(50 ℃时)为6～10 m2/s，密度为 0.85 g/cm3。

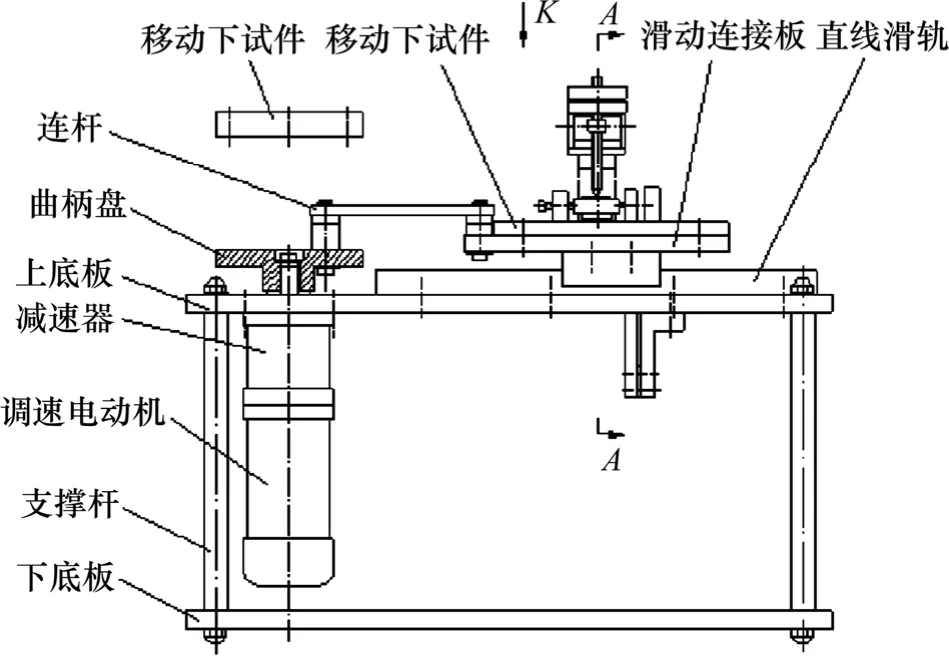
图1 摩擦试验机的总体结构图Fig.1 Structure of friction tester

测试软件系统可以实时智能显示仪表读数、当前摩擦力和摩擦因数等，并动态显示摩擦因数变化曲线。实验可以通过调速电机和加载砝码实现转速 0～200 r/min和微载荷0～1 N的调节。最终检测采用美国ADE公司的 MicroXAM 型非接触式表面形貌分析仪测量其三维表面形貌磨损体积，以磨痕深度来表征其磨损量；用JSM−6480型扫描电镜和Dimension型原子力显微镜观察磨痕的表面形貌。

2 实验结果与分析

2.1 表面形貌特征

MWEDM 的机理就是利用电能转换为热能蚀除金属。在高温熔融和急剧冷却作用下，加工表面的微观形貌特征表现为无数个随机分布的、圆滑的电蚀微凸峰和凹坑(如图2(a)所示)，且大小较为均匀，没有明显的纹理方向，表现为各向同性。而超精磨削加工表面由于存在明显的磨削刀痕(如图 2(b)所示)，表面纹理方向明显并呈周期性变化，波纹度也较大，呈各向异性[4]。二者微观结构存在很大不同。

图2 扫描电镜下加工表面形貌Fig.2 SEM morphologies of surfaces

2.2 表面支撑与液体滞留性能

在表面粗糙度测量中，支承面积率tp是用于表征表面微观形状特性的主要评定参数，可反映被测表面的表面性能。

根据 MWEDM 表面形貌特性，原子力显微镜取样面积为80 μm×80 μm，每个取样面积内至少包含3个峰或坑特征，选择至少5个取样，考虑表面峰的因素同时也为计算方便，把评定面积也确定为80 μm×80 μm，即扫描区域作为评定面积。

式中：tp为表面支撑面积率，SH为某截面高度H处的实体材料面积。计算不同水平截距下所对应的tp，得到不同加工方法表面支撑面积率曲线，如图3所示。

支承面积曲线分为峰顶区、核心区和谷底区3个区域[5−6]。由图3可见：MWEDM表面支承面积曲线两端变化率较小，中间部分(5%～80%)随高度变化很快；超精磨削加工表面的支承面积曲线整体表现为随高度均匀变化的趋势。MWEDM表面支承面积曲线线性区斜率比超精磨削加工表面的支承面积曲线斜率都大，中心区高度越小，说明中心区支承率增长越快，在同一高度水平上支承面积大，相同条件下MWEDM表面支承性越好，在工作寿命期内的磨损越小。

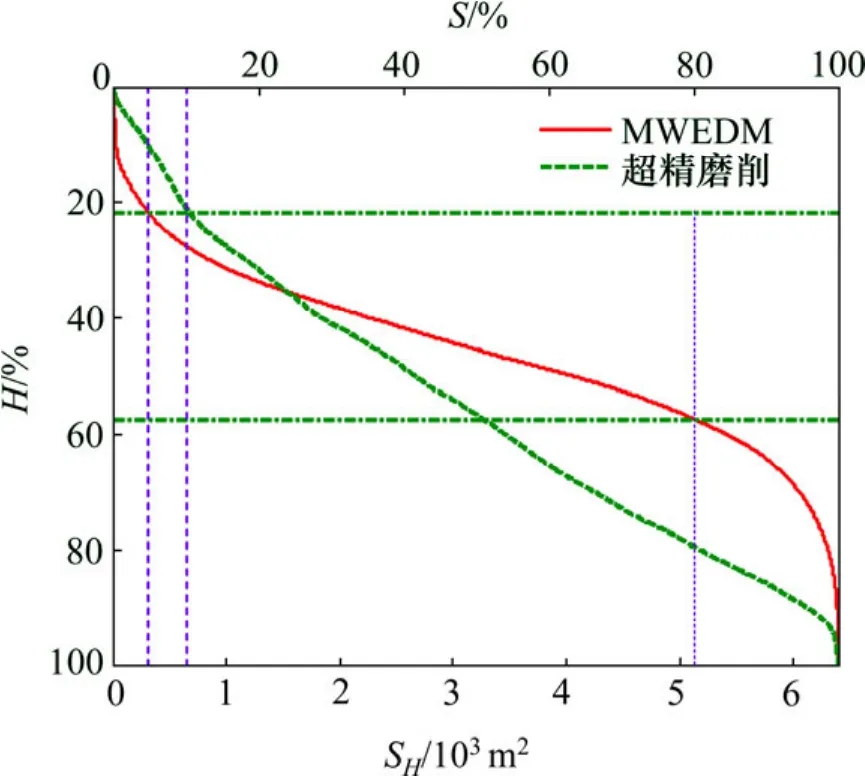
图3 不同加工表面的支承面积率曲线图Fig.3 Bearing area curves of different machined surfaces

在峰顶区，MWEDM表面支承面积随高度变化较慢，这是由于初始阶段只有少数凸峰进入接触状态，当所有凸峰都进入接触状态后，MWEDM表面支承面积随着高度稳定变化；对于超精磨削加工表面，在峰顶线附近的表面支承率比 MWEDM 表面的高，但随着峰顶线下降，支承率增大的速度较慢。而在稳定接触区，与超精磨削加工表面相比，MWEDM表面支承面积对高度变化很敏感，变化同样的高度其支承面积变化最大，且核心区容积和谷底区容积均较大，储油能力强，表明 MWEDM 表面比超精磨削加工表面支承性、液体滞留性和耐磨性均优。

2.3 MWEDM表面在润滑条件下的摩擦磨损性能

2.3.1 不同转速下的摩擦性能

选择微细3号为上试件，与其对比实验的上试件为同种材料、热处理状态与表面粗糙度Ra基本相同的超精磨削试件。2类试件分别与同一种摩擦配副在相同条件下进行往复滑动常温润滑试验，电动机输出轴转速分别为30，60，90，120和150 r/min，法向载荷为0.2 N。

润滑条件下 MWEDM 表面与超精磨削加工表面的摩擦因数与转速之间的变化关系曲线，如图4所示。从图4可见：

(1) 2种表面的摩擦因数都随转速的增加而减小。此时，润滑状态处于边界润滑向流体润滑状态转变，当载荷低于引起粘着磨损的临界值时，随着转速的增大，产生流体润滑膜，导致摩擦因数减小。

(2) MWEDM表面的摩擦因数比超精磨削加工表面的低8%～15%，尤其是在转速较高时降幅较大。按照流体润滑理论，由于高速运动的液体在两表面间的压力随间隙变小而液体压力增高的现象称为泵效应[7]。磨削表面如图 2(b)所示，是条条横向贯通的磨粒划痕，因而高压油容易泄出，使泵效应减弱。而MWEDM表面则不同，润滑油被挤压到凹坑中形成高压，并受到凹坑壁的阻拦不易泄出，因而油压升高快，泵效应显著。MWEDM表面与磨削表面相比，在较低转速下就可以形成油膜，在同样转速下，所形成的油膜压力高、油膜亦较厚， 更有利于保护零件工作表面而避免磨损。

图4 摩擦因数μ随转速n的变化曲线Fig.4 Relationship between friction coefficient and rotational speed

(3) 当转速达到120 r/min后磨削加工表面的摩擦因数随转速的增加反而增大，而 MWEDM 表面的摩擦因数变化不大。这是由于随着超精磨削加工表面与摩擦副表面之间相对滑动速度升高，在摩擦热的影响下，润滑油被稀释，承载能力下降，致使润滑油膜遭到破坏，接触峰点出现边界摩擦，导致摩擦因数突增，而MWEDM表面的摩擦因数受温升影响不显著。

对于不同电参数加工的 MWEDM 试件，摩擦因数之间的比较以及与转速变化的关系如图5所示。

由图5可见：单个脉冲放电能量最小的微细1号试件，虽然其表面最光滑，但摩擦因数却不是最小。由于放电能量的增加，温度梯度增大，热影响层的深度增加，放电点的表面温度升高，即放电通道中有更多的带电粒子以极高的速度轰击工件表面，使放电凹坑变深，因此，放电能量越大则加工表面就越粗糙[8]。随着凹坑深度的增加，凹坑的形状变化较大，合适的放电能量可以得到更规则的凹坑形貌[9]，从而影响动压润滑油膜的形成、厚度以及压力分布。

图5 不同电参数加工的试件摩擦因数μ与转速n的关系Fig.5 Relationship between friction coefficient and rotational speed of specimens under different electric parameters

通过有限元分析，获得一定参数下油膜动压力的的压力场分布状态，如图6所示。

图6 MWEDM表面单个微坑内的油膜压力场Fig.6 Oil film pressure field for single micro-pit on micro-WEDM surface

MWEDM表面形貌固有特征，导致复制形状于油膜压力分布图上的压力上下波动，这种形状复制使得粗糙表面的最大油膜压力比理想光滑表面的最大油膜压力大得多。而且表面粗糙度愈小，实际接触面积也愈大，由于表面分子吸引力有效地发生作用，从而使得摩擦因数增大，因此，粗糙表面与光滑表面之间有1个使摩擦因数为最小的表面粗糙度[10]。MWEDM表面在润滑状态下，根据不同的相对滑动速度，选用适宜的加工电参数，可获得较低的摩擦因数。本实验中微细2号件相对表现为佳，μ最低，下降幅度在0.02之间，变化波动小，稳定性好。

2.3.2 不同载荷下的摩擦性能

选择微细3号试件为上试件，对比实验的上试件与前面所述实验的试件相同。电动机输出轴转速为90 r/min，法向载荷分别为0.1，0.2，0.3，0.4和0.5 N。

摩擦因数同载荷之间的变化关系如图7所示。

图7 摩擦因数μ随载荷P的变化曲线Fig.7 Relationship between friction coefficient and loads

从图7可见：首先2种加工表面的摩擦因数都随载荷的增加而增大。这是因为：随着载荷的增大，油膜承受的压力增大，油膜变薄，促进摩擦方式由液体摩擦向固体摩擦转移，摩擦因数增加。其次，MWEDM表面的摩擦因数比磨削加工表面的摩擦因数小 10%～14%。在润滑情况下，两粗糙表面发生运动时，MWEDM表面上的凹坑就像许多微型水库，不仅可以滞留润滑油，而且可以为工作壁面提供润滑油，为贫油区补充润滑油，富油时就像很多滚珠轴承，起到产生良好流体动压力的效果[11−13]。当法向载荷增大时，MWEDM表面没有明显的纹理方向，以及放电微凹坑具有各向同性的特点，当在挤压的摩擦副间滴入润滑油时, 底部的润滑油得到保持，顶部的润滑油只能沿着凹坑周围的硬凸起流动；且微凹坑的三维形貌易于形成楔形收敛的间隙，从而利于在摩擦副表面之间形成动压油膜，在油膜中建立的与外加载荷相平衡的压力可将对磨表面近乎完全隔开，减少配副表面的直接接触，有效地减小MWEDM表面的摩擦，降低磨损。当载荷较低时 MWEDM 表面的摩擦因数与超精磨削加工表面的摩擦因数差距较小，随着载荷的增大两者的差距也变大，而 MWEDM 表面摩擦因数基本不受影响，变化幅度为0.006，表现出良好的稳定性。这是因为 MWEDM 表面在微载荷加载实验条件下，油膜未遭到破坏，润滑状态稳定，表现出良好的支承特性和储油特性。

对于不同电参数加工的试件，摩擦因数之间的比较以及与载荷变化的关系如图8所示。

图8 不同加工电参数的试件摩擦因数μ与载荷P的关系Fig.8 Relationship between friction coefficient and loads of specimens under different electric parameters

由图8可见：摩擦配副表面之间存在润滑油时，摩擦因数随载荷的增加而增大。虽然脉冲放电能量最小的微细1号试件的表面粗糙度低，摩擦因数却不是最小，而脉冲放电能量最大的微细6号试件的摩擦因数最大。随着载荷的增加，微细4号件摩擦因数变化最小，相对稳定。这说明由于 MWEDM 过程中采用的加工电参数的不同，导致加工表面微观形貌的主要组成部分微凹坑的数量、直径和深度的变化，从而使润滑油膜的承载能力有所不同。因此，在润滑状态下，根据不同的法向载荷，采用适当的加工电参数，可以使 MWEDM 获得具有较低的摩擦因数、摩擦及润滑性能最佳的表面，降低配副的磨损，延长使用寿命。

3 结论

(1) 基于MWEDM表面特性，其表面支承面积率从 0快速增加到5%，核心区容积和谷底区容积都较大，因此相同条件下，MWEDM表面的支承特性和液体滞留性均比超精磨削加工表面为优。

(2) 在不同转速情况下，2种表面的摩擦因数都随转速的增加而减小，MWEDM表面摩擦因数比超精磨削加工表面的低8%～15%，当转速达到一定数值后，超精磨削加工表面的摩擦因数出现上升拐点，而MWEDM表面摩擦因数无明显变化。

(3) 在不同载荷情况下，2种加工表面的摩擦因数都随载荷的增大而增大，MWEDM表面的摩擦因数比超精磨削加工表面的摩擦因数小10%～14%，且随着载荷的增加两者的摩擦因数差逐步加大。但是，MWEDM表面摩擦因数基本保持不变，表现出良好的摩擦磨损性能。

(4) 不同电参数加工的MWEDM表面在不同转速和不同载荷的润滑摩擦下，均处于边界和流体润滑状态，且摩擦因数稳定；合理选择 MWEDM 电参数既能提高加工效率，获得所需的加工表面，又能降低摩擦因数，使其保持良好的摩擦磨损性能。

[1] Pham D T, Dimov S S, Bigot S, et al. Micro-EDM: Recent developments and research issues[J]. Journal of Materials Processing Technology, 2004, 149(1/2/3): 50−57.

[2] DING Haijuan, GUO Libin, CUI Hai. Statistical characteristic and parameter characterization of 3D surface micro-topography on micro-EDM[C]// Proceedings of the IEEE International Conference on Automation and Logistics. Shenyang, China:IEEE Press, 2009: 1094−1098.

[3] 周仲荣. 摩擦学发展前沿[M]. 北京: 科学出版社, 2006:36−48.ZHOU Zhongrong. Tribology development frontier[M]. Beijing:Science Press, 2006: 36−48.

[4] 丁海娟, 崔海, 郭黎滨. 油润滑下微细电火花线切割加工表面的摩擦学特性[J]. 航空精密制造技术, 2011, 2(1): 30−33.DING Haijuan, CUI Hai, GUO Libin. Tribological properties of micro-WEDM surface under oil lubrication[J]. Aviation Precision Manufacturing Technology, 2011, 2(1): 30−33.

[5] Bigerelle M, Iost A. A numerical method to calculate the abbott parameters: A wear application[J]. Tribology International, 2007,40(9): 1319−1334.

[6] Schmahling J, Hamprecht F A. Generalizing the abbott-firestone curve by two new surface descriptors[J]. Wear, 2007, 262(11/12):1360−1371.

[7] 陆纪培, 田红宇. 电火花加工表面形貌对润滑性能的影响[J].电加工, 1985(6): 10−13.LU Jipei, TIAN Hongyu. Effect of electrical discharge machining surface morphology on lubrication performance[J].Electromachining, 1985(6): 10−13.

[8] 邵云鹏, 陆志猛. 放电参数对电火花线切割加工 Nd-Fe-B材料的影响[J]. 机械工程与自动化, 2009, 10(5): 87−89.SHAO Yunpeng, LU Zhimeng. Effect of discharge parameters on electrospark wire-electrode machining Nd-Fe-B[J].Mechanical Engineering & Automation, 2009, 10(5): 87−89.

[9] 程国柱, 刘志东, 田宗军, 等. 基于 ANSYS电火花线切割加工的温度场分析[J]. 电加工与模具, 2008(6): 24−26.CHENG Guozhu, LIU Zhidong, TIAN Zongjun, et al.Temperature field analysis based on ANSYS in WEDM[J].Electromachining & Mould, 2008(6): 24−26.

[10] 刘佐民. 摩擦学理论与设计[M]. 武汉: 武汉理工大学出版社,2009: 67−69.LIU Zuomin. Tribology theory and design[M]. Wuhan: Wuhan University of Science and Technology Press, 2009: 67−69.

[11] 李为松. 缸套微坑加工技术的应用基础研究[D]. 太原: 中北大学机械工程与自动化学院, 2007: 28−35.LI Wei-song. The application of basic research about tiny-pit cyclinder wall of processing technolngy[D]. Taiyuan: North University of China. College of Mechanical Engineering and Automation, 2007: 28−35.

[12] Kraker A D, Ostayen R A J, Rixen D J. Calculation of stribeck curves for (water) lubricated journal bearings[J]. Tribology International, 2007, 40(3): 459−469.

[13] Kumar R, Kumar S, Prakash B, et al. Assessment of engine liner wear from bearing area curves[J]. Wear, 2000, 239(2): 282−286.