填充床固态发酵生物反应器模拟研究进展
2012-12-27董吉林申瑞玲
董吉林 杜 冰 申瑞玲
(1.郑州轻工业学院食品与生物工程学院,河南 郑州 450002;2.华南农业大学食品学院,广东 广州 510642)
填充床固态发酵生物反应器模拟研究进展
董吉林1杜 冰2申瑞玲1
(1.郑州轻工业学院食品与生物工程学院,河南 郑州 450002;2.华南农业大学食品学院,广东 广州 510642)
数学模型是固态发酵生物反应器设计、优化和操作的重要工具,它不仅可以指导SSF过程生物反应器的设计和操作,而且可以深入分析发酵系统内的各种现象从而控制整个发酵过程。文章分析近几年固态发酵填充床生物反应器的拟均相假设模拟模型、非均相假设模拟模型和间歇混合填充床生物反应器模拟模型,对模拟结果进行讨论,深入分析如何用数学方法描述SSF系统的传热传质模型。在分析填充床固态发酵底物床层的系统组成及其性质的基础上,提出利用多孔介质体积平均理论研究SSF系统传热传质过程的可能性。
固态发酵;填充床;生物反应器;模拟;拟均相假设;非均相假设;多孔介质;体积平均理论
近年来,固态发酵(solid-state fermentation,SSF),即微生物在没有或几乎没有游离水的潮湿水不溶性固体底物中的生物反应过程,越来越受到研究者的关注。研究[1,2]表明,固态发酵最大的优点是底物材料成本低、利用率高,在次级代谢产物产生和积累方面有着明显的优势。农产品加工残渣碳水化合物等营养素丰富,非常适合于丝状真菌的生长,所以,SSF是农产品加工残渣的良好利用途径[3],在食品工业、生物工程等领域具有极大应用前景。
但农产品加工残渣在固态发酵时存在底物成分不均、缺乏自由水及固体颗粒传导性较差等缺点,使得对发酵过程的生物量、pH值、温度和湿度等培养参数的控制难度较大,相应的研究也主要集中在底物的优化和菌种的筛选上[4,5],而对发酵床层热/质量传递数学模型研究较少,因此,制约了SSF生物反应器的可控操作,阻碍了SSF过程应用和扩大。
数学模型是SSF生物反应器设计和优化操作的重要工具,它概括了固态发酵系统内复杂的相互作用和如何操作的相关知识,不需要研究大量的试验结果图表,可以在建造大型生物反应器之前预测反应器的生产能力、优化设计参数和操作条件。即使预测不完全准确,这种建模工作也比“最优猜测”或“反复试验”方法获得成功的可能性更大。建成大型生物反应器并经过测试后,则可以用大型生物反应器的新数据来修改模型,并将其作为优化生物反应器操作的工具,它不仅可以指导生物反应器的设计和操作,预测发酵过程中的一些重要变量,而且可以深入分析发酵系统内的各种现象,了解微生物固态发酵过程的机理,减少试验次数及费用。
为此,建立固态发酵生物反应器的数学模型,利用计算机模拟技术模拟其生产性能,确定影响生产性能的关键设计参数和操作参数,对设计和制造固态发酵生物反应器具有直接指导作用,可以为固态发酵的工业化及工业化过程中实现发酵全过程的监控和优化控制奠定基础,提高农产品的综合利用水平,使其变废为宝,产生良好的生态效益、经济效益和社会效益。
1 填充床生物反应器的模拟现状
大部分SSF过程的微生物都是真菌,这些真菌生长越快,释放的代谢热也越多,但由于缺乏自由水且固体颗粒的传热性又较差,导致底物床层出现温度梯度。尽管混合可以极大地改善反应器器壁的热移出,但连续或频繁混合时产生的剪切力和碰撞力会伤害真菌菌丝或底物,因此,发酵过程(至少大部分时间)中底物床层必须采用静态操作[6]。目前,只有浅盘式生物反应器和填充床生物反应器采用这种操作模式,浅盘式生物反应器中,空气不通过床层,只有浅盘表面移出热量,如果空气沿浅盘循环或在浅盘上安装冷却板,则可以促进热移出,但床层仍出现较大的温度梯度和湿度梯度,所以浅盘式生物反应器的床层高度只有几厘米,限制了发酵底物的数量[7]。填充床生物反应器利用强力通风移出大量热量,使其床层高度较高,但空气流经固体床层时,固体床层仍出现轴向温度梯度,加快水的蒸发,使床层变干,影响微生物的生长及代谢物质的产生,限制了填充床生物反应器的性能[8]。
填充床SSF是一个四相系统[9],流经固体床层的通风空气或混合气体是连续相,含营养素的水不溶性固体物质是固相,水不溶性固体所吸附的液体是液相,固体表面、内部及其间隙生长的微生物是第4相(如图1所示)。其中水不溶性固体颗粒主要是农产品或农产品加工副产品等天然物质。
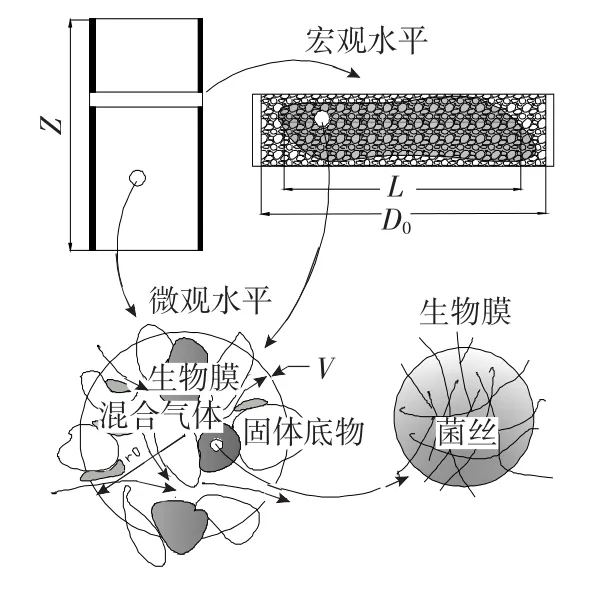
图1 填充床固态发酵生物反应器床层示意图Figure 1 The schematic of packed-ded solid state fermentation bioreactor
目前,主要采用两种方法模拟填充床反应器,即将床层看作拟均相和非均相。如果假设填充床为拟均相,则空气和固体床层不是相互独立的两相,而是处于热平衡和水平衡,床层是具有空气和底物质量权重平均特性的单一“拟均相”,这种简化假设只适合通风空气是饱和的情况,空气从床层一侧流向到另一侧,使得底物床层出现温度梯度和浓度梯度[7],而研究[10]表明温度梯度是限制生物反应器的性能的主要因素,所以,温度控制和热传递成为大部分填充床生物反应器,特别是大型生物反应器的主要研究对象,完全忽略了其它重要的质量传递。
1.1 拟均相假设的模拟进展
拟均相单相系统数学模型主要求解能量平衡方程,Saucedo-Castaneda等[11]开发了第一个填充床生物反应器模型,试验采用直径6cm、高35cm带水夹套冷却的圆柱形生物反应器,并用表面速度较低的空气促进径向传热,由于底物床层直径只有6cm,生物反应器可以通过器壁传导移出大部分代谢废热,模型只考虑了径向传导传热,忽略了轴向传热,但模型无法预测圆柱底部5cm的轴向温度梯度,也无法合理描述径向温度曲线。Hasan等[12]在此基础上开发了一个两维热传递数学模型,描述了填充床固态发酵生物反应器发酵米糠时的热传递,模型预测与试验的径向温度梯度和轴向温度梯度一致,模拟结果表明床层宽度增加到一定程度后,通过器壁移出的热量逐渐减少,而床层轴向温度梯度较大,空气表面流速是影响温度梯度的最大因素,床层传热主要是对流传热。某些数学模型考虑了蒸发对传热的影响,模拟结果证实蒸发是系统热移出的主要原因,即使空气是饱和空气,蒸发也可移出2/3的热量[8,13]。拟均相假设数学模型还用于扩大研究[14]、生物反应器预防过热机理的确定[8]和发酵型填充床生物反应器的分析[15]。这些模型假设底物中的所有水分都可蒸发,没有考虑水活度对生长的影响,其能量平衡只描述了蒸发传热,没有考虑水平衡,所以这种模型只适合发酵过程中水的蒸发不会严重影响底物水活度的情况,即选择湿度变化较大但水活度变化较小的底物。
1.2 非均相假设的研究进展
在选择固态发酵的底物时需要考虑多种因素,有时必须利用某种特定农产品加工废料,且多数底物含水量减少时,水活度都会显著下降,蒸发移出热量的同时也使床层湿度下降,床层变干,为此,模型必须将固体颗粒和颗粒间气相看作两个独立相,并描述二者间能量平衡和水质量平衡。Weber等[16]用拟稳态假设建立了能量平衡和水平衡,完全忽略了温度瞬时变化和热焓蓄积,模拟结果表明床层进风口的轴向温度梯度最高,且轴向温度梯度随轴向距离的增加而逐渐下降,水蒸气浓度与轴向距离呈线性关系。填充床生物反应器是单向空气对流冷却,所以一定会出现轴向温度梯度,随发酵的进行底物床层的水活度也会变化。为控制轴向温度梯度,Sahir等[17]将底物床层分成高度相同的N个多层填充床生物反应器,建立数学模型后预测了蛋白酶的生产。Mitchell等[18]利用该数学模型研究了多层填充床生物反应器使用3种操作方案时的性能,即空气流经N个床层而床层不移动、N个床层每隔1h循环移动的分批操作和N个床层连续活塞式移动且在空气入口加入新床层而在空气出口移出发酵完成床层。在模拟条件下,连续活塞式移动稳态中所产生的代谢热是常规操作时产热的60%,其最高床层温度比常规操作低4.5℃。结果表明,连续活塞流操作模式可以极大地提高多层填充床的生产性能。
2 间歇混合填充床生物反应器的模拟现状
研究[19,20]表明,多数真菌在生长动力学影响不大的情况下可以忍受相对较少的混合,搅拌期间既可以补充床层因蒸发而丧失的水分,又可以恢复静态期真菌菌丝生长而下降的床层孔隙度。所以,间歇混合生物反应器的应用前景较大。
已经建造了大量与填充床相类似间歇混合填充床SSF生物反应器,底物床层大部分时间都是静态模式,区别是生物反应器包括一个搅拌器,可以进行间歇搅拌。这种生物反应器的静态操作期与填充床生物反应器类似。模拟[21]表明,混合后很短时间就重新建立了填充床操作的拟稳态温度曲线,由于通风冷却主要集中在生物反应器较低区域,所以,床层顶部温度超过填充床的操作温度,如果要想使顶部温度低于拟稳态温度,则必须每隔一定时间就混合一次。Von Meimen等[22,23]以微生物对剪切力敏感的SSF过程为研究对象,采用静态操作最佳,但可以忍受间歇混合的操作模式,研究开发了一个描述强制通风间歇混合生物反应器热传递和水传递的两相模型,模型表明如果微生物可以忍受较少的混合,则用相对较少的混合和补充水程序可以最小化水活度对生长的限制,但在这种静态操作期较长的大型生物反应器中不可能完全消除水的限制。
从填充床固态发酵生物反应器的系统组成及底物性质来看,填充床固态发酵床层是一个多孔介质系统(如图1所示)[24]。多孔介质的多相体系非常复杂且具有随机性,即使简化了介质的周期性和规则性,也很难确定多孔介质中流体的变量和传递,很难对多孔介质结构进行完整的宏观描述和微观描述,必须用动态系数模型才能克服线性或非线性传递模型的缺点,而多相系统使传递机制的研究和传递现象的模拟更加复杂[25,26]。
目前,主要采用Whitaker体积平均理论研究多孔介质传热传质过程[27,28]。Whitaker体积平均理论用真实物性的体积平均值描述多孔介质内部的传热传质过程,可以清晰容易地理解传热传质过程,也较容易确定所用参数,Whitaker在多孔介质中选取一个表征体元(representative elementary volume,REV),当表征体元大到足以满足反映宏观效应时,则可以认为该体积单元上的某些属性平均值和现象具有一定的连续性和代表性,从多孔介质局部结构,即固、液、气相在多孔介质中的微观结构和微观现象出发来研究和分析多孔介质的属性和内部传递规律,并将其扩大成为多孔介质的宏观属性和现象[29,30]。因此,可以利用多孔介质体积平均理论经严格数学推导建立填充床固态发酵的宏观传热传质数学模型,清晰容易地理解固态发酵过程中的传热传质过程,确定所用参数。
3 展望
填充床固态发酵床层是一个多孔介质系统。因此,未来可以利用Whitaker多孔介质体积平均理论,从多孔介质局部结构,即固、液、气相在多孔介质中的微观结构和微观现象出发来研究和分析多孔介质的属性和内部传递规律,并将其扩大成为多孔介质的宏观属性和现象,可以建立填充床固态发酵的宏观传热传质数学模型,清晰容易地理解传热传质过程,确定所用参数,对设计和制造固态发酵生物反应器具有直接指导作用,可以为固态发酵的工业化及工业化过程中实现发酵全过程的监控和优化控制奠定基础,提高农产品的综合利用水平。
1 Robinson T,Singh D,Nigam P.Solid-state fermentation:a promising microbial technology for secondary metabolite production[J].Apply of Microbiology Biotechnology,2001,55(3):284~289.
2 廖春燕,郑裕国.固态发酵生物反应器[J].微生物学通报,2005,32(1):99~103.
3 姚跃飞,曾柏全.现代固态发酵技术在食品加工业中的应用[J].食品与机械,2005,21(6):89~92.
4 倪林,李春葆,李世艳,等.一株分解纤维素放线菌的诱变选育及其固态发酵条件[J].合肥工业大学学报:自然科学版,2011,34(12):1 873~1 876.
5 顾斌,马海乐,刘斌.菜籽粕混菌固态发酵制备多肽饲料的研究[J].中国粮油学报,2011,26(1):83~87.
6 Hamidi-esfahani Z,Shojaosadati S A,Rinzema A.Modelling of simultaneous effect of moisture and temperature onA.nigergrowth in solid-state fermentation[J].Biochem.Eng.J.,2004,21(3):265~272.
7 Khanahmadia M,Roostaazadb R,Mitchellc D A,et al.Bed moisture estimation by monitoring of air stream temperature rise in packed-bed solid-state fermentation[J].Chemical Engineering Science,2006,61(17):5 654~5 663.
8 Fanaei M A,Vaziri B M.Modeling of temperature gradients in packed-bed solid-state bioreactors[J].Chem.Eng.Process,2009,48(1):446~451.
9 Rahardjo Y S P,Tramper J,Rinzema A.Modeling conversion and transport phenomena in solid-state fermentation:A review and perspectives[J].Biotechnology Advances,2006,24(2):161~179.
10 Pandey A.Solid-state fermentation[J].Biochem.Eng.J.,2003,13(2-3):81~84.
11 Saucedo-Casteneda G,Gutierrez-Rojas M,Bacquet G,et al.Heat transfer simulation in solid substrate fermentation[J].Biotechnol Bioeng,1990,35(8):802~808.
12 Hasan S D M,Costa J A V,Sanzo A V L.Heat transfer simulation of solid-state fermentation in a packed bed bioreactor[J].Biotechnol Tech.,1998,12(10):787~791.
13 Mitchell D A,von Meien O F,Krieger N.Recent developments in modeling of solid-state fermentation:heat and mass transfer in biore-actors[J].Biochem.Eng.J.,2003,13(2-3):137~147.
14 Mitchell D A,Pandey A,Sangsurasak P,et al.Scale-up strategies for packed-bed bioreactors for solid-state fermentation[J],Process Biochem.,1999,35(1-2):167~178.
15 Mitchell D A,von Meien O F.Mathematical modelling as a tool to investigate the design and operation of the Zymotis packedbed bioreactor for solid-state fermentation[J].Biotechnol Bioeng,2000,68(2):127~135.
16 Weber F J,Oostra J,Tramper J,et al.Validation of a model for process development and scale-up of packed-bed solid-state bioreactors[J].Biotechnol Bioeng,2002,77(4):381~393.
17 Sahir A H,Kumar S.Modelling of a packed bed solid-state fermentation bioreactor using the N-tanks in series approach[J].Biochem.Eng.J.,2007,35(1):20~28.
18 Mitchell D A,Cunhaa L E N,Machadoa A V L,et al.A model-based investigation of the potential advantages of multi-layer packed beds in solid-state fermentation[J].Biochemical Engineering Journal,2010,48(2):195~203.
19 Fernández M,Pérez-Correa J R,Solar I,et al.Automation of a solid substrate cultivation pilot reactor[J].Bioprocess Engineering,1996,16(1):1~4.
20 Bandelier S,Renaud R,Durand A.Production of gibberellic acid by fed-batch solid state fermentation in an aseptic pilotscale reactor[J].Process Biochemistry,1997,32(2):141~145.
21 Durand A.Bioreactor designs for solid state fermentation[J].Biochemical Engineering Journal,2003,13(2-3):113~125.
22 Von Meimen O F,Mitchell D A.A two-phase model for water and heat transfer within an intermittently-mixed solid-state fermentation bioreactor with forced aeration[J].Biotechnology and Bioengineering,2002,79(4):416~428.
23 Von Meiena O F,Jra L F L,Mitchell D A,et al.Control strategies for intermittently mixed,forcefully aerated solid-state fermentation bioreactors based on the analysis of a distributed parameter model[J].Chemical Engineering Science,2004,59(21):4 493~4 504.
24 董吉林.填充床固态发酵生物反应器生产性能的模拟研究[D].广州:华南农业大学,2010.
25 Golfier F,Wood B D,Orgogozo L,et al.Biofilms in porous media:Development of macroscopic transport equations via volume averaging with closure for local mass equilibrium conditions[J].Advances in Water Resources,2009,32(3):463~485.
26 李栋,涂郑禹,李贤宇,等.具有非均匀内热源的多孔介质中自然对流传热传质的数值研究[J].四川化工,2010,13(1):35~38.
27 宫克勤,孙苗苗.多孔介质中传热传质机理研究[J].油气田地面工程,2009,28(4):15~16.
28 王璐瑶,潘艳秋,王维,等.吸湿多孔介质冷冻干燥传质传热模型[J].干燥技术与设备,2011,9(2):82~93.
29 谢英柏,苏杭,刘春涛,等.含湿多孔介质对流干燥的不可逆热力学模型[J].华北电力大学学报,2009,36(2):48~53.
30 Rashad A M,EL-Hakiem M A,Abdou M M M.Natural convection boundary layer of a non-Newtonian fluid about a permeable vertical cone embedded in a porous medium saturated with a nanofluid[J].Computers and Mathematics with Applications,2011,62(8):3 140~3 151.
Review of recent developments in modeling of packed-bed solid-state fermentation bioreactors
DONGJi-Lin1DU Bing2SHEN Rui-Ling1
(1.School of Food and Biological Engineering,Zhengzhou University of Light Industry,Zhengzhou,Henan450002,China;2.College of Food Science,South China Agricultural University,Guangzhou,Guangdong510642,China)
Mathematical models are important tools for optimizing the design and operation of solid-state fermentation(SSF)bioreactors.Not only can models guide the design and operation of bioreactors but they can also provide insights into how the various phenomena within the fermentation system combine to control overall process performance.The current article evaluates the proposed models of Packed-Bed Solid-State Fermentation Bioreactors that hypothesis the substrate bed to be treated as a single pseudohomogeneous phase or nonpseudohomogeneous phase,and intermittently-mixed packed-bed bioreactors.The insights that have been achieved through the modeling work and the advances that have been made in heat and mass transportation models are discussed.In addition,the improvements of porous media volume averaging theory to heat and mass transportation models that will be necessary in the future are discussed.
solid-state fermentation;packed-bed;bioreactor;modeling;pseudohomogeneous phase hypothesis;nonpseudohomogeneous phase hypothesis;porous media;volume averaging theory
10.3969/j.issn.1003-5788.2012.03.070
郑州轻工业学院博士科研基金资助项目(编号:2010BSJJ017)
董吉林(1968-),男,郑州轻工业学院副教授。E-mail:djl1968@163.com
2012-02-15
