车辆振动对机枪射击密集度的影响分析

李洪强，廖振强，王 涛，咸东鹏

（南京理工大学 机械工程学院，南京210094）

武器的动态特性对射击密集度的影响最终体现在枪口的动态响应上，射弹散布与弹丸出枪口瞬间的枪口位置参数有一定的对应关系.因此，研究持续射击过程中机枪枪口的位置参数是研究机枪射击密集度的重要依据.影响弹丸出枪口时刻枪口位置参数的因素很多，除去装药误差等不可控因素外，发射平台的动态响应，即发射平台在射击过程中的振动及变形是影响枪口参数的主要因素.

而对于大口径车载机枪，由于其发射威力大，后坐体作用在发射平台上的后坐力大，过大的后坐力一方面引起托架及摇架发生较大的变形，另一方面改变了车辆的平衡稳定性，导致车辆轮胎与地面接触力的变化，引起车辆的整体振动，从而降低机枪的射击密集度.在通常的机枪设计中，为了提高机枪的射击密集度，往往是从对机枪架座（主要为托架、摇架等）的设计改进着手，一般忽视了车辆振动对机枪射击精度的影响.而实验表明，车辆的振动是影响车载机枪射击密集度的重要因素，对于大口径车载武器而言，必须考虑车辆结构参数对机枪射击密集度的影响.因此，本文从车辆振动的角度出发，分析车辆的状态对机枪射击密集度的影响规律.

1 基本理论

1.1 车辆与地面接触理论

轮胎是车辆中重要的组成部分，其基本功能包括支撑车辆及其负载；与悬挂系统共同作用，抑制车辆的振动；传递纵向力实现车辆的加速、驱动及制动等.在研究车辆振动对机枪射击精度的影响时，轮胎与悬挂系统的振动是研究车辆振动的核心，研究轮胎与地面的接触是研究车载武器发射动力学的重要环节.图1为按照轮胎数据交换国际标准的轮胎与地面接触的作用力及约定符号，图中x′、y′、z′分别为车轮中心平面方向、侧向力方向及垂直路面方向，Ω、T分别为车轮绕轴心方向的回转角速度及扭矩，Mx、My、Mz分别为轮胎的翻转力矩、轮胎与地面之间的滚动阻力矩及回正力矩，Fx、Fy、Fz分别为轮胎的纵向力、侧向力及垂直力，α、γ分别为轮胎的侧偏角与外倾角[1].

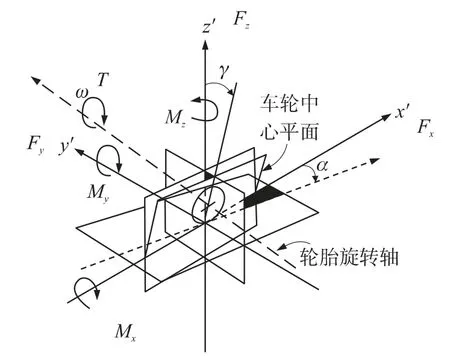
图1 轮胎与地面作用力及符号表示

轮胎的垂直力为

式中，Kz为轮胎的径向刚度，Cz为轮胎的径向阻尼系数，δ为轮胎径向压缩高度.

纵向力与侧向力的计算由轮胎运动状态决定，取轮胎运动时轮胎中心的切向速度为vx，轮胎的切向滑移速度为vsx，轮胎转动的角速度为ω，轮胎的有效滚动半径为Re，轮胎法向的速度为vsy，轮胎运动时的滑移率为Ss＝－vsx/vx，侧偏角为tanα＝vsy/

认为轮胎与地面的摩擦系数是与轮胎滑移系数线性关系的函数，取f＝fmax－（fmax－fmin）Ssα.式中，fmax、fmin分别为静摩擦系数与动摩擦系数.

定义轮胎纵向临界滑移系数Sc及临界侧偏角αc为

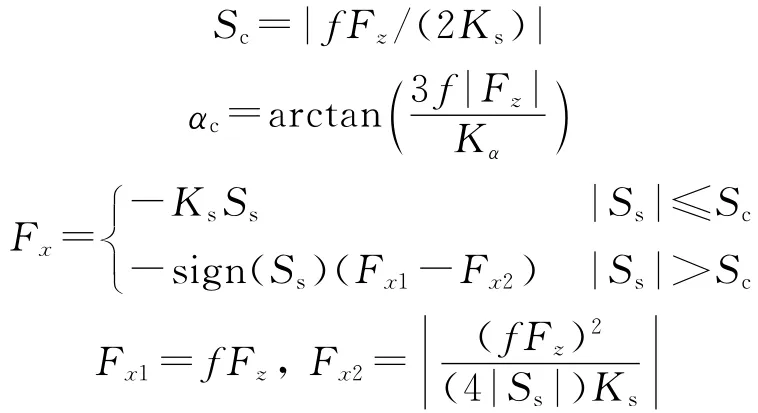
当｜α｜≤αc时，

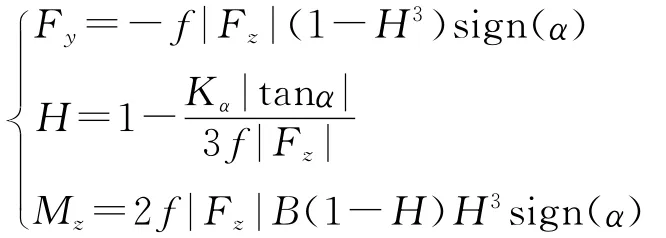
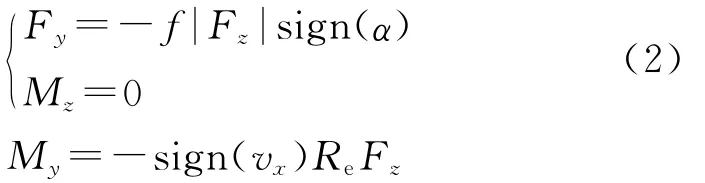
式中，Ks为纵向滑移刚度，Kα为侧偏刚度，B为轮胎的侧向宽度[2].

1.2 随机路面谱理论

车辆在路面行驶时，路面环境对车体的运动影响较大，为了便于分析，将车辆行驶的路面高度认为沿水平路面的随机函数，取路面相对基准平面的高度h沿路程l的变化h（l）为路面不平度，路面波的波长为λ时，其空间频率为σ＝1/λ，路面不平度h（l）截断函数hl（l）[3]为

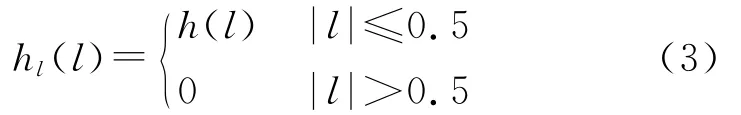
阶段函数hl（l）在空间频率σ的傅里叶变换为

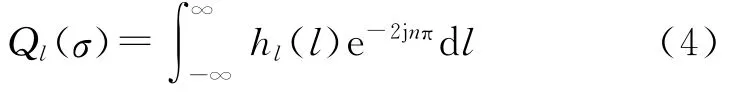
取路面谱Gq（σ）为

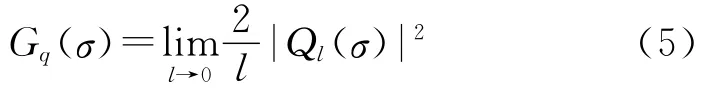
按照国际标准建议，上式拟合的路面功率谱密度函数为

当｜α｜＞αc时，

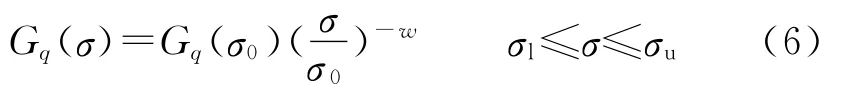
式中，σ为空间频率，代表每米长度上包含σ个波长；σu，σl分别为路面谱的上、下空间频率；参考空间频率σ0＝0.1m－1；Gq（σ0）为参考空间频率σ0下的路面谱值，称为路面不平度系数；w为频率指数[4].

2 发射动力学模型

计算模型采用某3管14.5 mm口径内能源转管机枪，车载机枪由机枪、摇架、托架、座圈及其支撑件和车辆组成.机枪射击过程中后坐体后坐能量通过缓冲装置作用在摇架上，通过托架及座圈等零件的传递作用在车辆上.由于射击过程中作用在发射平台上的后坐能量大，发射平台产生局部变形，因此基于多体动力学理论，本文建立了刚柔耦合的车载转管机枪动力学模型，模型中将枪管托架、摇架、座圈及其支撑架等零部件通过有限元软件柔性化处理，这些零部件在射击过程中可能产生较大变形，对射击精度具有较大影响，而将车辆本体视为刚性体进行分析.各柔性体之间通过柔性体上关联的刚性点传递力及力矩，车辆悬架减震系统采用弹簧阻尼系统描述[5].系统模型及其坐标见图2.

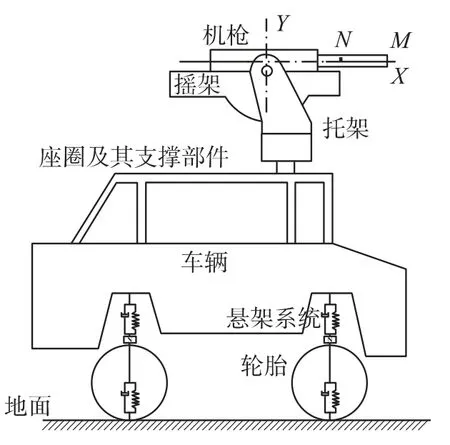
图2 车载机枪结构模型

2.1 机枪动力学设置

转管机枪自动循环工作的能量来自于机枪射击时膛内火药气体压力的作用，通过引出部分膛内火药气体，驱动活塞往复运动，从而在空间曲线槽的作用下实现枪管组及机心体的转动，达到转管机枪自动循环工作的目的.因此，膛内火药气体压力的计算及导气室内气体压力的计算是机枪动力学分析的关键.内弹道时期膛内火药气体压力由经典内弹道方程得到，根据气体动力学的理论得到后效期阶段膛内气体压力，导气室气体压力采用气体动力学的计算方法，通过建立导气室内气体动力学方程组，计算导气式气体压力参数的变化规律[6].

2.2 轮胎刚度的计算

轮胎的径向弹性除了受到轮胎外形尺寸的影响，轮胎的内压也是影响轮胎径向弹性的主要因素，匈牙利柯曼太以各种轮胎尺寸与胎压在混凝土路面上进行了大量实验，提出了轮胎压缩量δ的经验公式：

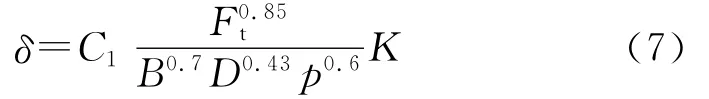
式中，C1为与轮胎结构有关的参数，斜交轮胎为1.15，子午轮胎为1.5；p为轮胎内压（100kPa）；Ft为轮胎载荷 （9.8N）；D、B分别为轮胎的直径与宽度，cm；K为与轮胎截面宽度B相关的常数.

轮胎的径向刚度为

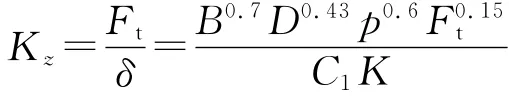
在轮胎胎压保持不变的情况下，轮胎的径向刚度随轮胎载荷的大小一起变化，当汽车载荷在一定范围内变化时，轮胎径向刚度变化量小，Ft以轮胎负载的平均值替代.

轮胎与地面的纵向滑移物理模型为轮胎橡胶块在地面切向力的作用下产生剪切变形和弯曲变形.根据材料力学的理论，长、宽、厚分别为a、b、d的矩形橡胶块在切向力F的作用下变形量为

式中，E、G、I分别为橡胶的弹性模量、抗剪弹性模量及截面惯性矩，A为橡胶块截面积（A＝ab）.

取橡胶在单位作用力下产生的变形为橡胶的侧向弹性常数C，其表达式为

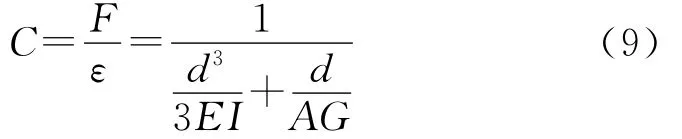
根据轮胎学的相关理论，轮胎的纵向滑移刚度为

式中，B为轮胎的宽度，L为轮胎接地长度[7].

3 模型计算

计算模型中路面选择平坦刚性水泥路面，忽略地面的变形.依据Iso8608标准，路面等级选择B级随机路面，轮胎左右两侧路面相同，机枪的稳定射频为3 000min－1，模型分别计算了车辆在自由状态下、前轮制动、后轮制动以及在增大车辆前胎的刚度时机枪的射击精度.初始状态下车辆在后坐能量的作用下可自由运动，车辆前胎的刚度为140N/mm，后胎的刚度为145N/mm.计算模型初始时将车辆水平放置在刚性水泥路面，分析模型初始时车辆处于静止状态，机枪处于水平状态朝车辆前方射击，车辆侧偏角α与外倾角γ为0，在机枪后坐力的作用下，一方面车辆沿枪管轴线方向向后运动，另一方面在后坐力及偏心力矩的作用下，车辆的稳定性条件发生变化，任意轮胎与地面之间的径向力发生变化，引起车辆的振动.分析模型采用Adams软件计算，采用fiala轮胎模型.

计算模型中，为了描述方便，取沿枪管轴线向枪口方向为X轴正方向，垂直路面向上方向为Y轴正方向，其坐标系见图2.沿X轴在枪管上分别取M、N两标志点，M点位于枪口位置，N点在M点左侧距枪口位置933 mm.分析时通过计算弹丸出枪口时刻M、N两点在Y坐标上的位移差ΔY，研究车辆状态对机枪射击密集度的影响.

3.1 车辆制动状态对射击密集度的影响

为研究车辆的制动状态对射击精度的影响，分析了3种状态下的机枪射击时在高低方向上托架的最大振动角度β1与车辆的最大振动角度β2，以及在弹丸出枪口时刻M、N两点在Y方向的位移差ΔY.车辆分别处于前轮制动状态、后轮制动状态以及车辆自由状态.其计算结果见表1及图3～图5.表1中R70为计算70%的有效射弹量在100m靶距位置上其最小散布圆半径.

表1 车辆制动状态对射击密集度的影响分析结果

图3～图5的计算结果表明：①在车辆振动达到最大角度后，制动状态下车辆的振动趋于稳定，车辆保持在相对于初始状态的高振动角度，自由状态下，车辆的振动具有一定程度的起伏，车辆保持稳定状态的能力较差，自车辆振动达到最大振动角度后，在后续的射击过程中，自由状态、前轮制动及后轮制动状态下车辆的振动角度与最大振动角度的差值分别为0.62°、0.14°与0.05°；②每一次击发过程中托架部件的振动变形相近，射击初始阶段托架的变形较大，射击稳定后其相对变形趋于稳定逐渐减小；③在射击初始阶段ΔY变化明显，其原因归结为射击初始阶段托架的振动剧烈，初始射击阶段弹丸离群是影响射击密集度的重要因素，射击稳定后ΔY的变化趋于稳定；④车辆制动状态下，ΔY值相对自由状态偏大，射弹的高低分布中心相对于自由状态偏高；⑤制动状态下尤其是后轮制动状态下射击密集度比自由状态好，射击精度高，根据计算，自由状态、前轮制动及后轮制动状态下其射击精度分别为9.4mil，6.8mil，5.3mil，试验测得自由状态下机枪的射击精度为9.2mil，这反映了所建立的模型是准确、合理的；⑥车辆振动很大程度上影响了机枪射击密集度，射击过程中通过制动车辆的方法能较好地抑制车辆对机枪射击密集度的不利影响，并且射击过程中制动后轮对提高射击密集度具有明显效果.

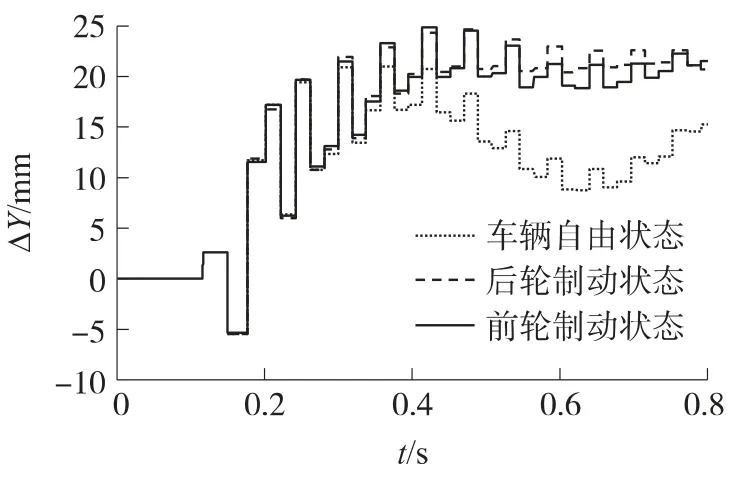
图3 不同车辆制动状态下ΔY值变化曲线

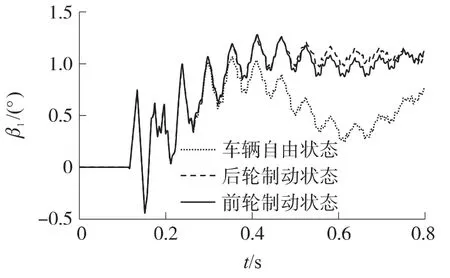
图4 不同车辆制动状态下托架振动曲线

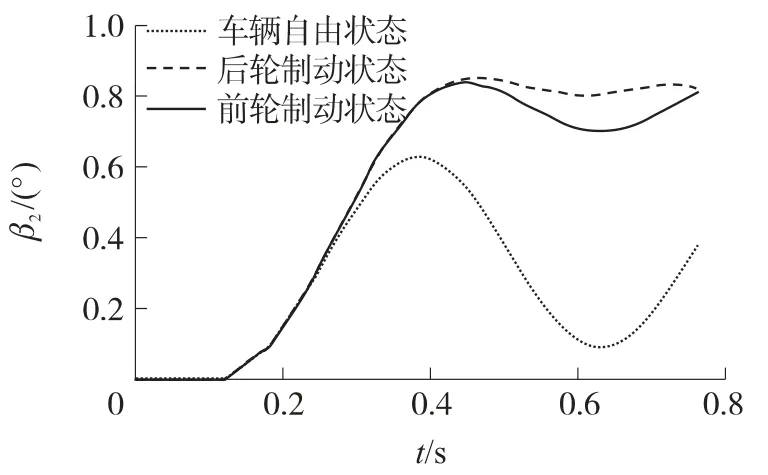
图5 不同车辆制动状态下车辆振动曲线

3.2 轮胎刚度对射击密集度的影响

为了研究轮胎的刚度对射击密集度的影响，模型分析了车辆处于自由状态时，3种轮胎刚度状态下的机枪射击时动力学响应，前轮刚度K分别为140N/mm，200N/mm及250N/mm.通过分析，得出了表2及图6～图8所示的计算结果.

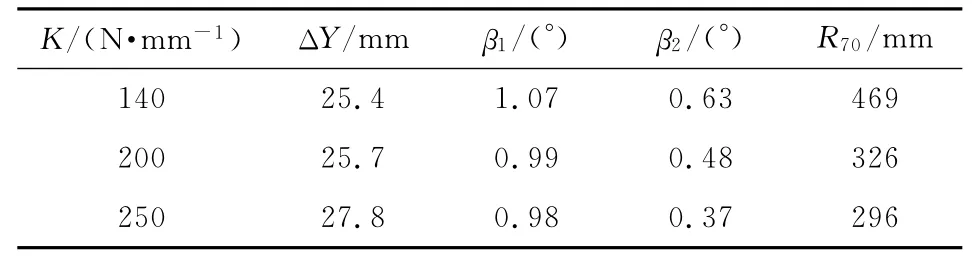
表2 前胎刚度对射击密集度的影响分析结果

图6 不同轮胎刚度下ΔY值变化曲线

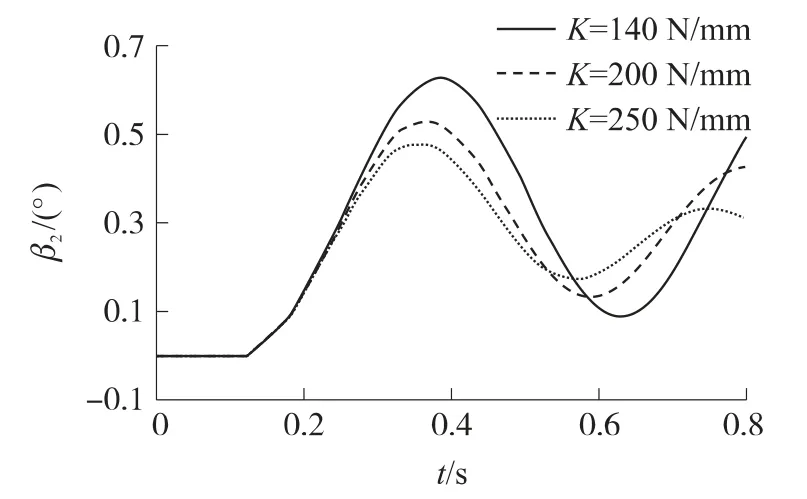
图7 不同轮胎刚度下车辆振动曲线

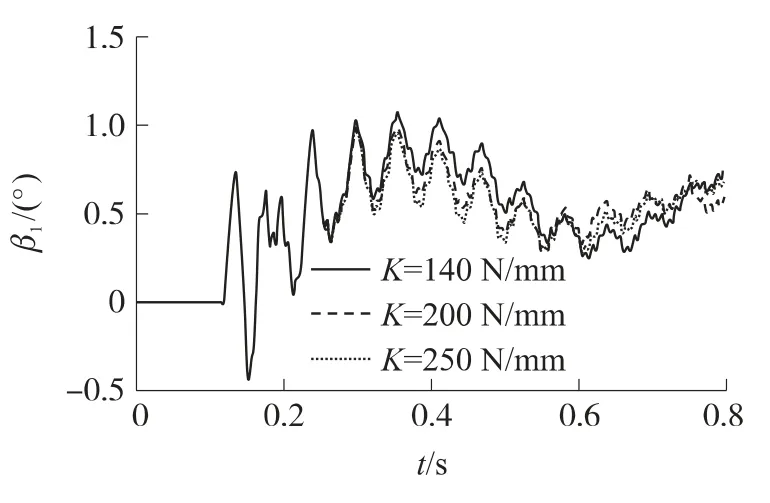
图8 不同轮胎刚度下托架振动曲线

图6～图8的计算结果表明：①轮胎的刚度越大，车辆保持稳定状态的能力越好，自车辆振动达到最大振动角度后，在后续的射击过程中，前胎刚度为140N/mm，200N/mm及250N/mm的状态下车辆的振动角度与最大振动角度的差值分别为0.62°，0.4°与0.3°；②轮胎刚度越大，车辆的最大振动角度越小；③轮胎刚度越大，ΔY值越大，射弹的高低分布中心越高；④轮胎刚度越大，由于车辆振动引起的负面影响越小，射击密集度越高，根据计算，前胎刚度为140N/mm，200N/mm及250N/mm的状态下其射击精度分别为9.4mil，6.5mil，6mil；⑤通过增大轮胎刚度，车辆振动与托架振动比例减小，说明了车辆振动对射击密集度的不利影响程度得到抑制.

4 结论

通过上述分析可以得出：①车辆振动对车载机枪的射击密集度具有重要影响，控制车辆振动是发展车载机枪的重要研究方向；②车辆制动状态下车辆保持稳定的性能明显比车辆自由状态下好，射击密集度高，是提高车载机枪射击密集度的有效途径，并且制动后轮的效果更显著；③车轮刚度增大对于提高车辆的稳定性有利，车辆的最大振动角度减小，车辆振动的不利因素得到抑制，能有效地提高机枪的射击密集度；④车辆制动与提高车辆前胎的刚度都会引起在高低方向上射弹中心的偏高，对于瞄准射击低矮目标不利.并且，车辆制动状态下车辆的最大振动角度偏大，这些会给车载机枪的射击和操作带来一定程度的负面影响.

[1]陈军.Msc.ADAMS技术与工程分析实例[M].北京：中国水利水电出版社，2008.CHEN Jun.Analysis example of Msc.ADAMS technology and engineering[M].Beijing：China WaterPower Press，2008.（in Chinese）

[2]任卫群.车路系统动力学中的虚拟样机[M].北京：电子工业出版社，2005.REN Wei－qun.Virtual prototype of the car road system dynamics[M].Beijing：Publishing House of Electronics Industry，2005.（in Chinese）

[3]毛保全，张金忠，杨志良，等.车载武器发射动力学[M].北京：国防工业出版社，2010.MAO Bao－quan，ZHANG Jin－zhong，YANG Zhi－liang，et al.Launch dynamics of vehicle weapon[M].Beijing：National Defense Industry Press，2010.（in Chinese）

[4]程刚，张相炎，董志强，等.轮式自行高炮行进间射击稳定性仿真研究[J].兵工学报，2010，31（2）：149－153.CHENG Gang，ZHANG Xiang－yan，DONG Zhi－qiang，et al.Simulation research on stability of firing on－the－move for wheeled self－propelled anti－aircraft gun[J].Acta Armamentarii，2010，31（2）：149－153.（in Chinese）

[5]毛保全，王国辉，杨志良，等.车载武器建模与仿真[M].北京：国防工业出版社，2012.MAO Bao－quan，WANG Guo－hui，YANG Zhi－liang，et al.Modeling and simulation of vehicle weapon[M].Beijing：National Defense Industry Press，2012.（in Chinese）

[6]陆家鹏，谭兴良，雷志义，等.自动武器气体动力学[M].南京：南京理工大学，1989.LU Jia－peng，TAN Xing－liang，LEI Zhi－yi，et al.Gas dynamics of automatic weapons[M].Nanjing：Nanjing University of Science and Technology，1989.（in Chinese）

[7]庄继德.汽车轮胎学[M].北京：北京理工大学出版社，1996.ZHUANG Ji－de.Theory of car tire[M].Beijing：Beijing Institute of Technology Press，1996.（in Chinese）