导弹协同制导中末交接班目标截获概率研究

付昭旺，于 雷，寇英信，徐 安

（空军工程大学 工程学院，西安710038）

多机协同空战已成为现代空战的主要作战模式，导弹协同攻击是协同作战的核心，而协同制导是导弹协同攻击的关键环节，直接影响协同作战效果.近年来，国内对导弹协同制导问题展开了研究，内容涉及协同制导的原理和关键技术[1，2]、协同制导决策方法[3，4]、导弹协同制导的导引律[5]等.协同制导条件下，发射载机和制导载机相分离，制导交接误差、目标参数测量误差、载机定位误差和导弹传递对准误差等误差源会降低修正指令的精度，直接影响导弹中制导的效果.目前对于导弹协同制导的制导能力和制导效果缺乏研究.文献[6]对协同制导条件下的中、末交接班能力进行了一些研究，但是考虑的误差因素简单，未建立误差传递模型，无法对误差影响下的制导精度进行定量评估.基于此，本文通过对协同制导的信息流和误差源传递进行分析，并建立误差源与目标截获概率的定量模型，为导弹协同制导效果评估提供理论依据.

1 导弹协同制导数学建模

以典型的双机协同制导为例进行建模研究，将发射导弹的载机称为交班载机（Quit Fighter，QF），将参与接替制导的载机称为接班载机（Succeeded Fighter，SF）.制导交接后，QF退出，由SF接替制导，以周期T向导弹发送指令，修正其飞行方向和姿态，在满足中末制导交接条件时，导引头开机搜索，截获目标后转入末制导.

1.1 制导惯性坐标系的建立

为实现协同制导，必须建立一个统一的制导惯性坐标系，制导惯性坐标系由QF建立并完成与导弹的传递对准，并通过制导交接传递给SF.本文建立如下制导惯性坐标系：导弹发射前与QF传递对准完成时刻，以QF所在位置的“北、天、东”地理坐标系作为制导惯性坐标系.

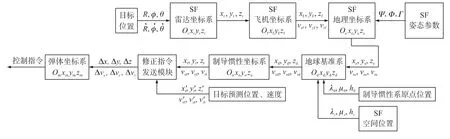
图1 协同制导修正指令计算流程

1.2 协同制导修正指令的计算流程

协同制导修正指令的计算需要经过多次坐标转换.本文建立如图1所示的修正指令计算流程.文中相关坐标系的定义及转换关系见文献[7].QF和SF的地理位置均采用WGS－84地球模型定义的经度、纬度和海拔高度来表示.图1中，R，φ，θ为SF雷达测得的目标参数，分别为目标距离、方位角及俯仰角；xr，yr，zr为Orxryrzr下的目标位置；xf，yf，zf和vxf，vyf，vzf分别为SF在Ofxfyfzf下的目标位置和速度；Ψ，Φ和Γ分别为SF的机体航向角、俯仰角和滚转角，xe，ye，ze为Oexeyeze下的目标位置；λ0，μ0，h0（经度、纬度和高度）为Odxdydzd下Ooxoyozo的原点所在的位置；λz，μz，hz为Odxdydzd下SF所在的空间位置；xd，yd，zd为Odxdydzd下的目标位置；xt，yt，zt和vxt，vyt，vzt分别为Ooxoyozo下的目标实际位置和速度；x′t，y′t，z′t和v′xt，v′yt，v′zt分别为目标预测的位置和速度；Δx，Δy，Δz和 Δvx，Δvy，Δvz分别为目标的位置偏差和速度偏差.

1.3 修正指令计算模型

根据修正指令计算流程，以位置修正指令计算为例，给出其矢量法计算方法，速度修正指令的计算与位置修正指令计算类似.

Orxryrzr系下的目标位置为

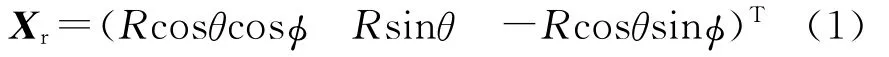
Ofxfyfzf下的目标位置为

式中，Tf，r为Orxryrzr到Ofxfyfzf的转换矩阵.

Oexeyeze下的目标位置为

式中，Te，f为Ofxfyfzf到Oexeyeze的转换矩阵.

Odxdydzd下的目标位置为

式中，Xde为Odxdydzd下Oexeyeze原点的位置，Td，e为Oexeyeze到Odxdydzd的转换矩阵.

Ooxoyozo下目标的位置为

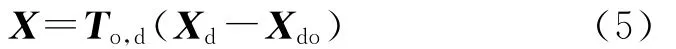
式中，Xdo为Odxdydzd下Ooxoyozo原点的位置，To，d为Odxdydzd到Ooxoyozo的转换矩阵.

设计算得到t时刻Ooxoyozo下的目标位置X和目标速度vt，设t时刻导弹预测的目标位置为X′、预测速度为v′t，则对目标的位置修正和速度修正指令分别为ΔX＝X－X′和Δv＝vt－v′t.

2 导弹协同制导误差模型

导弹协同制导包括目标参数测量、指令计算、指令传输和弹体运动等过程.指令计算需要引入SF的空间位置和姿态参数，并经过多次坐标转换，与单机自主制导相比，协同制导误差源增多，对制导精度产生影响.为研究协同制导的效果，必须对协同制导误差进行建模分析.

2.1 影响协同制导的主要误差源

协同制导引入的误差源主要有以下6项：①SF雷达的测量误差；②SF的空间定位误差；③SF姿态测量误差；④QF与导弹的传递对准误差；⑤修正指令延时误差；⑥导弹的状态估计误差.这6种误差源相互独立，作用于导弹中制导的不同环节，其中，①、②、③和④产生和影响修正指令的计算误差，⑤和⑥影响指令的执行误差，它们都直接影响导弹中末交接班的交接效果.

2.2 误差特性分析

雷达测量误差可以认为是一种服从零均值正态分布的随机误差，可采用测距精度δR和测角精度δφ、δθ来描述；载机姿态测量误差与姿态传感器的测量精度有关，可采用姿态角误差δΨ、δΦ和δΓ来描述；载机的空间定位误差由飞机导航系统产生，由于载机的地理位置采用经度、纬度和高度来表示，SF的空间定位误差可采用经度误差δλz、纬度误差δμz和高度误差δhz来度量；传递对准误差由导弹惯性坐标系O′ox′oy′oz′o与制导惯性系Ooxoyozo之间存在失准角δω而引入，δω的大小可由载机火控系统和武器系统的性能参数得到；指令延时误差是由于SF修正指令延时而影响导弹对目标机动的准确估计，可以等同于目标机动估计误差，指令延时误差主要由制导交接延时、SF与QF的系统时钟偏差、指令接收延时和指令处理延时引起；导弹状态估计误差由弹载惯导引起，与导弹的工作时间和飞行轨迹有关，具有累积效应，可采用惯导精度δm来描述.

2.3 误差计算模型

设SF雷达测距误差为δR，方位测角误差为δφ，俯仰测角误差为δθ，则由机载雷达测量引起的目标位置估计误差为

考虑雷达测量误差，式（1）中的Xr变为

Ofxfyfzf下的目标估计位置为

考虑 QF的姿态误差，式（3）中的Te，f变为

则Oexeyeze下的目标估计位置为

同理，考虑到SF的空间定位误差，有：

则Odxdydzd下的目标估计位置为

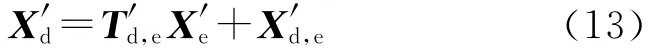
Ooxoyozo下的目标位置为

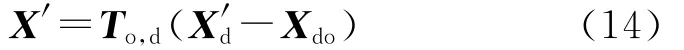
考虑导弹发射的传递对准误差，导弹惯性系O′ox′oy′oz′o下目标的估计位置为

式中，反对称矩阵Tω＝f（δωx，δωy，δωz）.

在修正指令延时Δt内，导弹以目标作匀速直线运动进行位置估计，但是，导弹发射后，目标必然进行逃逸机动，则指令延时引入误差为对目标的机动估计误差，可采用下式进行计算[2]：

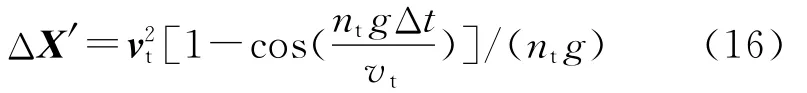
式中，nt为目标过载，vt为目标速度.

在上述误差源叠加作用下，O′ox′oy′oz′o下的目标位置估计误差为

所有误差源相互独立，于是O′ox′oy′oz′o下目标位置估计误差的方差可表示为

导弹惯性导航系统的定位误差可表示为

式中，δm为惯导的定位精度，t为导弹飞行时间.

则O′ox′oy′oz′o下导弹位置估计误差的方差为

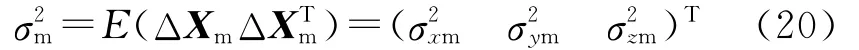
由于 ΔXe和 ΔXm相互独立，于是O′ox′oy′oz′o下导弹和目标相对位置估计误差的方差为

Omxmymzm下目标位置估计误差的方差为

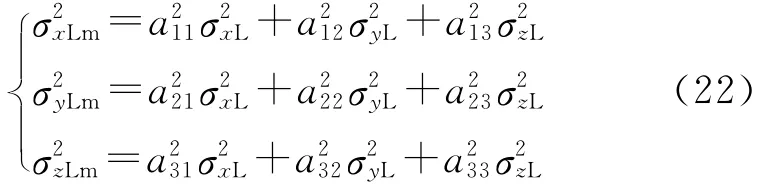
式中，aij（i，j＝1，2，3）为导弹惯性坐标系到弹体坐标系的转换矩阵中的系数.

3 目标截获概率计算模型

中末制导交接班的目标截获包括角度截获、距离截获和速度截获，分别设三者的截获概率为Pa、Pr和Pv，则目标截获概率可以表示为

本文主要研究导引头的角度截获问题，令Pr＝Pv＝1.角度截获概率是指目标实际视线落入雷达导引头视场的概率，取决于导弹的导引头指向误差和导引头视场的宽度.导引头指向角误差φa只需考虑垂直于导引头视线平面的y轴和z轴方向的分量φya和φza.φa的概率分布应取决于二维随机变量（φya，φza）的概率密度函数[8]：

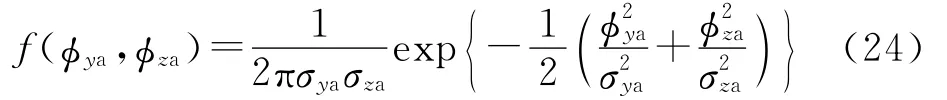
式中，σka＝arctan（σkLm/Ds）（k＝y，z），Ds为导引头的预定交班距离[2].

由于角度截获需要方位和俯仰同时满足截获条件，令σa＝max（σya，σza），则有：

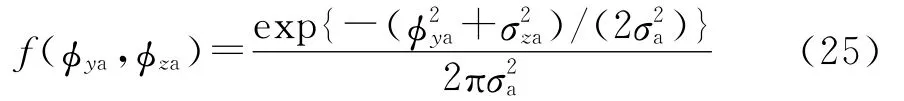
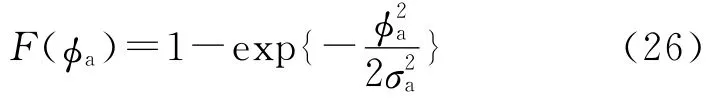
设导引头半视场的宽度为α，则有：

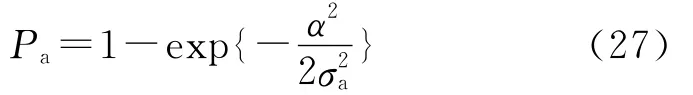
4 协同制导截获概率仿真研究

根据所建立的模型对协同制导目标截获概率进行仿真.针对每种误差源条件仿真N次，对误差进行统计，再根据统计量计算截获概率.仿真条件设置如下：λ0＝110.105°，μ0＝60.051°，h0＝6km；导弹初速vm＝450 m/s，α＝2.5°，导引头的预订交班距离Ds＝15km.目标初始位置为：xt＝30km，yt＝8km，zt＝0，vt＝1 080km/h，ψt＝－40°.导弹发射后目标以6g的过载作水平蛇形机动.SF的初始位置：λz＝110.366°，μz＝59.722°，hz＝10km，Ψz＝30°，vz＝900km/h.SF 与 目 标 的 初 始 距 离 为68.3km，指令周期为0.5s，取N＝50，P0＝1，仿真误差条件如表1所示.

表1 仿真误差条件

仿真得到中末交班平均时间为31.65s，一次典型的弹道轨迹如图2所示.目标估计位置与实际位置相比存在动态估计误差，该误差将直接影响中末交接班的目标截获概率.

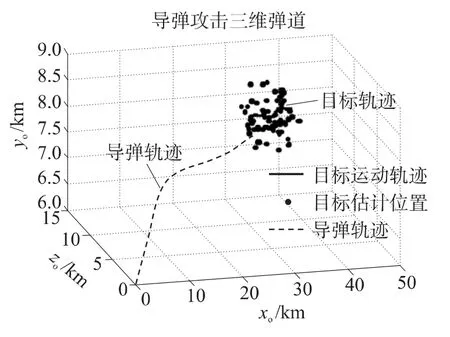
图2 协同制导仿真弹道轨迹曲线

为定量分析各误差对Pa的影响，保留初始条件不变，依次逐项改变误差项进行仿真.仿真结果如图3～图7所示.

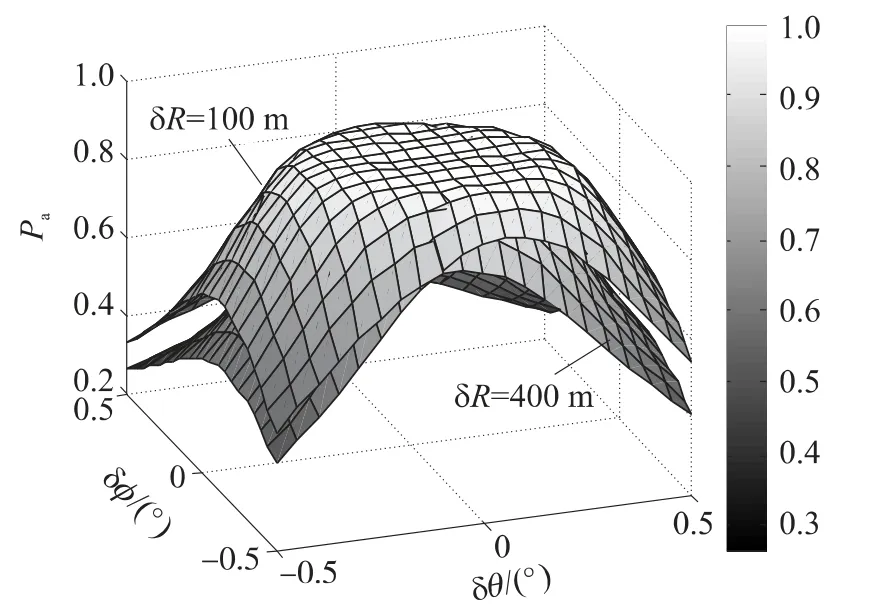
图3 δR，δφ和δθ与Pa的关系

图4 δΨ和δΦ与Pa的关系

图5 δλz和δμz与Pa关系

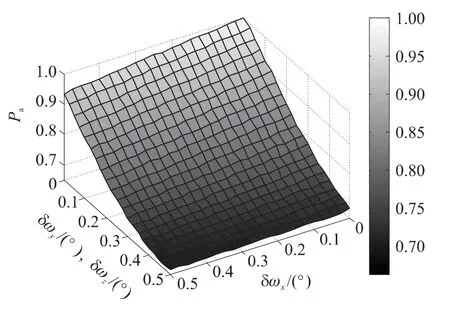
图6 δω与Pa的关系

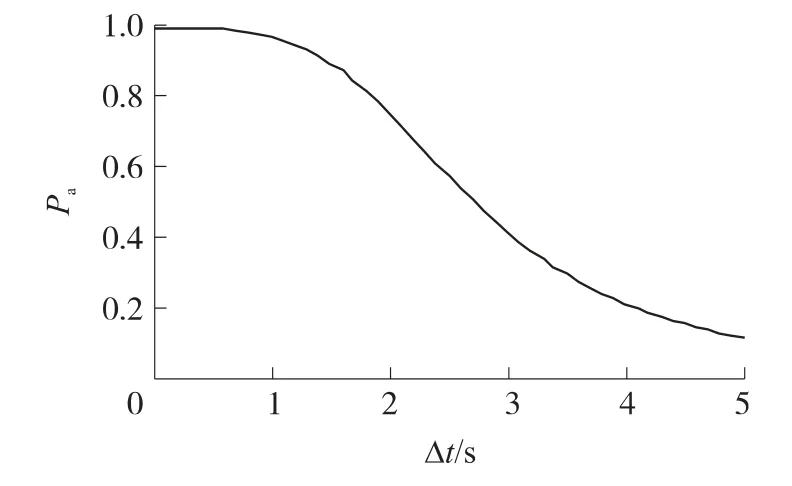
图7 Δt与Pa的关系曲线

由图3可以看出，SF雷达测角精度较高时，对Pa影响很小，δφ＜0.2°且δθ＜0.2°时，Pa≥0.98，测角误差增大时，对Pa影响增大，在δφ＞0.2°且δθ＞0.2°时，Pa随δφ和δθ的增大而迅速下降，当δφ＞0.5°且δθ＞0.5°时，Pa＜0.5.

由图4可以看出，SF姿态测量精度较高时，对Pa影响很小，δΨ＜0.15°且δΦ＜0.15°时，Pa＞0.98，测量误差增大时，对Pa影响较大.

由图5可以看出，SF空间定位误差对Pa影响较小，在δλz＝δμz＜0.000 5°时，Pa＞0.96，在δλz＝δμz＜0.001 5°时，Pa＞0.8.

由图6可以看出，Pa对小幅度的传递对准误差较为敏感，而随着误差的增大，敏感度降低，总体来看，影响不明显.

由图7可以看出，Δt较小时，对Pa影响很小，Δt＜0.8s时，Pa＞0.98，Δt增大时，Pa随 Δt增大而迅速下降，Δt＞2.7s时，Pa＜0.5.

显然，各误差源对截获概率的影响程度不同，但是影响趋势大致类似.为了对比各误差源对Pa的影响，对Pa进行灵敏度分析，以E表示灵敏度，以ΔSX表示参数X的相对误差，得到如图8所示的灵敏度曲线.由图8可以看出，Pa对Δt的敏感性最高，其次是机载雷达测量误差，而对空间定位误差敏感性最低.在相对误差较小时（小于0.6），Pa对传递对准误差的敏感性较高，反之，对姿态测量误差敏感性更高.

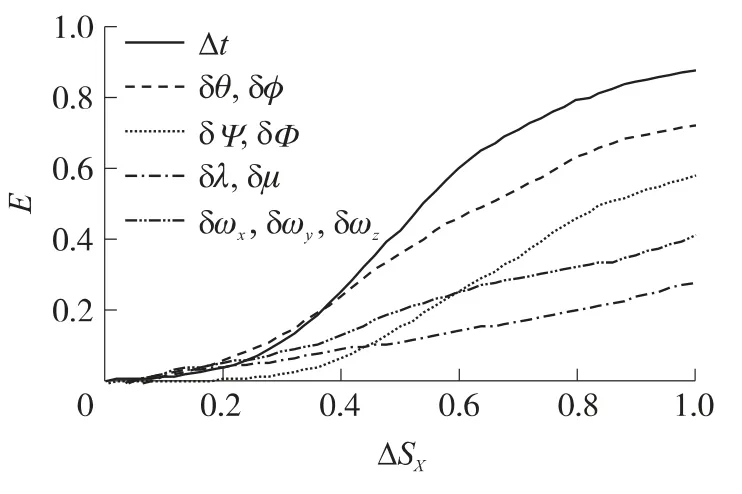
图8 误差源的灵敏度曲线

综上所述，为提高协同制导的目标截获概率，可采取如下措施：①协同编队应建立精确的统一时钟来保证协同制导精确的时间同步；②对协同制导的SF进行决策，尽可能选择雷达测量精度高或距目标较近的SF进行制导；③为SF装备高精度惯导系统或采用组合导航技术，提高其姿态测量精度和定位精度；④提升QF与导弹的传递对准精度，在导弹完成精对准后再发射.

5 结束语

本文基于协同制导的信息流和误差传递关系对协同制导精度进行建模研究，得到了误差源与目标截获概率之间的定量分析模型，并对误差灵敏度进行了仿真分析.结果表明：修正指令的延时误差、制导载机的雷达测量精度和姿态精度对目标截获概率影响较大，建立高精度的协同数据链，并选择雷达性能优良的载机进行协同制导是非常必要的.本文的研究为导弹协同制导作战效果评估奠定了基础，并对导弹协同制导的作战应用具有一定的参考价值.需要指出的是，本文仅考虑了制导交接后的制导误差，没有对制导交接引入的误差进行分析，下一步需要对不同制导交接条件下的制导精度进行建模研究.

[1]高坚，佟明安.双机编队协同制导的火控机理[J].火力与指挥控制，2009，34（12）：38－40.GAO Jian，TONG Ming－an.Fire control principle on cooperative guidance with two－fighters team[J].Fire Control ＆ Command Control，2009，34（12）：38－40.（in Chinese）

[2]肖冰松，方洋旺，许蕴山.双机协作发射与制导中程空空导弹技术研究[J].电光与控制，2009，18（2）：13－16.XIAO Bing－song，FANG Yang－wang，XU Yun－shan.Technologies for dual－fighter’s cooperative launching and guiding of medium range air－to－air missiles[J].Electronics Optics ＆ Control，2009，18（2）：13－16.（in Chinese）

[3]肖冰松，方洋旺，胡诗国.多机空战协同制导决策方法[J].系统工程与电子技术，2009，31（3）：56－60.XIAO Bing－song，FANG Yang－wang，HU shi－guo.Decision methods for cooperative guidance in multi－aircraft air warfare[J].Systems Engineering and Electronic，2009，31（3）：56－60.（in Chinese）

[4]刁兴华，方洋旺，王鹏.对地攻击协同制导决策方法[J].电光与控制，2011，18（3）：52－55.DIAO Xing－hua，FANG Yang－wang，WANG Peng.Cooperative guidance decision－making in air－to－ground attacking[J].Electronics Optics ＆ Control，2011，18（3）：52－55.（in Chinese）

[5]ZHAO Shi－yu，ZHOU Rui.Cooperative guidance for multi－missile salvo attack[J].Chinese Journal of Aeronautics，2008，21：533－539.

[6]牛晓川，陈少华，吴宗一，等.协同制导条件下空空导弹中末制导交接班能力[J].弹箭与制导学报，2011，31（4）：41－45.NIU Xiao－chuan，CHEN Shao－hua，WU Zong－yi，et al.Investigation of air－to－air missile’s midcourse and terminal guidance handing－off based on cooperative guidance[J].Journal of Projectiles，Rockets，Missiles and Guidance，2011，31（4）：41－45.（in Chinese）

[7]周志刚.航空综合火力控制原理[M].北京：国防工业出版社，2008.ZHOU Zhi－gang.Synthesis fire control principle for aviation[M].Beijing：National Defense Industry Press，2008.（in Chinese）

[8]付海峰，刘华伟，张宗麟.中距主动制导空空导弹目标截获概率仿真计算[J].电光与控制，2007，14（3）：55－58.FU Hai－feng，LIU Hua－wei，ZHANG Zong－lin.Simulated computation of target－acquisition probability of medium－range active－guided AAM[J].Electronics Optics ＆ Control，2007，14（3）：55－58.（in Chinese）