基于复合执行机构的再入弹头动力学建模与控制
2012-12-25蒋方超
王 振,吴 忠,蒋方超
(北京航空航天大学 仪器科学与光电工程学院,北京100191)
作为一种强有力的威慑和打击手段,弹道导弹在现代战争中起着举足轻重的作用.为提高弹道导弹的命中精度,增强机动突防能力,必须对弹道导弹的再入弹头进行末制导.再入弹头的姿态控制是末制导所要解决的核心关键技术之一.
为实现再入弹头的姿态控制,目前主要采用气动舵面控制、推力矢量控制、变质心控制等方案.气动舵面控制和推力矢量控制方案在工程上已有多年的实践历史,技术相对较为成熟.然而,实践表明气动舵面存在高温烧蚀、控制效率不高等问题[1].推力矢量控制虽不存在上述问题,但会引起弹体质心漂移,侧向喷流与来流的相互影响也会产生一定的干扰,影响弹体的控制性能[2].
变质心控制方案则将质量滑块安装在弹头内部,不存在烧蚀问题,结构简单[3~5],已成功应用于“白杨”M等导弹中[6].国内对变质心控制方案的研究起步较晚,但已取得一些有价值的研究成果[7,8].然而,仅依靠质量滑块不能产生滚转控制力矩,在大气稀薄时,无法实现较大幅度的姿态机动[3].
为避免以上方案存在的问题,文献[9]将航天器控制领域中常用的姿态控制执行机构——动量轮引入再入弹头的控制.与变质心控制类似,动量轮同样不存在烧蚀问题.然而,动量轮所能提供的力矩有限,不足以实现弹头较大的机动控制[6,9].
同样,单框架控制力矩陀螺(SGCMG)也是一种航天器姿态控制执行机构[10],利用较小的框架运动即可输出较大的力矩,不依赖外部环境,动态特性好,适于高机动再入弹头的姿态稳定与控制[6].然而,当SGCMG产生常值力矩时,可能会发生角动量饱和问题,需要借助卸载执行机构进行卸载.
考虑到质量滑块和SGCMG特点的互补性,可采用SGCMG辅助质量滑块工作,而通过质量滑块调节气动力矩为SGCMG卸载,取长补短.当弹头位于大气层外或大气较为稀薄时,以SGCMG为主,以质量滑块为辅;当弹头位于大气层内或大气较为稠密时,以质量滑块为主,以SGCMG为辅.然而,如何将质量滑块和SGCMG复合使用以实现弹头再入控制,目前尚未见系统的研究工作.
因此,本文针对采用质量滑块和SGCMG 2类执行机构的再入弹头,采用New-Euler法,详细建立基于复合执行机构的再入动力学模型,利用Lyapunov稳定性理论,设计弹头非线性姿态控制器,以实现对期望姿态的良好跟踪,并通过仿真手段,分析复合执行机构在再入弹头控制中应用的可行性.
1 坐标系及符号定义
设再入弹头采用2个质量滑块(p、q)和n个SGCMG作为姿态控制执行机构,整个系统的质心为S,弹头本体的质心为O,压心为P,如图1所示.所用坐标系定义如下.
①惯性坐标系OExiyizi(i系).选为地心赤道惯性坐标系.
②再入坐标系exeyeze(e系).e为再入时刻地心OE与再入弹头质心O的连线与地球表面的交点,eye沿e点与质心O的连线方向,指向质心O为正,exe在再入时刻再入弹头运行的轨道平面内,且垂直于eye轴.
③再入弹头体坐标系Oxbybzb(b系).O为再入弹头质心,Oxb沿纵轴指向头部,Oyb在纵向对称平面内,向上为正,Ozb由右手定则确定.
④平台坐标系Opxpypzp(p系).用于安装SGCMG,Op与O重合,Opxp、Opyp、Opzp分别与弹体坐标系的Oyb、Ozb、Oxb轴重合.
⑤框架坐标系Gisigiti(Gi系).框架坐标系随框架一起转动,Gi为第i个SGCMG的质心,Gisi沿转子转动轴方向,Gigi沿框架转动轴方向,如图2所示.

图1 再入系统结构示意图及坐标系定义

图2 SGCMG结构示意图及坐标系定义
为方便推导,定义变量及符号如下:
m为弹头和SGCMG的总质量;mp,mq分别为质量滑块p和q的质量;再入系统总质量mt=m+mp+mq;质量比μp=mp/mt,μq=mq/mt.
rs为质心S的绝对矢量,ro为质心O的绝对矢量,ros为质心S相对质心O的矢量;rsp为质量滑块质心p相对质心S的矢量;rsq为质量滑块质心q相对质心S的矢量;p,q分别为质量滑块p和q相对质心O的位置矢量;vp,vq分别为质量滑块p和q的绝对速度矢量.
Ag= (g1g2…gn),As= (s1s2…sn),At=(t1t2…tn),其中,gj,sj,tj分别表示SGCMG的框架角速度方向单位矢量、转子转速方向单位矢量和输出力矩反方向单位矢量在b系中的分量列阵,j=1,2,…,n;Icg,Ics,Ict分别为SGCMG(包括框架和转子)对g,s,t轴的转动惯量对角矩阵;Iws为SGCMG转子轴向转动惯量对角矩阵;Ω=(Ω1Ω2…Ωn)T为SGCMG的转子角速度;(Ω)d=diag(Ω1,Ω2,…,Ωn),上标“d”表示对角变换;γ=(γ1γ2…γn)T为SGCMG的框架角=(12…n)T为框架角速度.
G为再入系统重力;Fa为空气动力;Mo为空气动力对质心O的力矩;Ms为空气动力对质心S的力矩;Md为空气阻尼力矩.
Jo为再入弹头对质心O的转动惯量;J为再入系统总的转动惯量.
(·)w表示矢量(·)在w系中的投影表示从u系到w系的坐标变换矩阵表示w系相对u系的角速度在 w 系中的投影分别表示矢量r相对u系的一阶、二阶导数在w系的投影;如果x=(x1x2x3)T,则
2 再入弹头动力学建模
设再入系统各部分为刚体,视质量滑块均为质点,考虑地球自转角速度、非球形等因素的影响.同时,设质量滑块的布局是任意的,p和q的移动路径均用矢量表示,n个SGCMG的安装也是任意的.
2.1 平动动力学
再入系统质心S在惯性系中可表示为
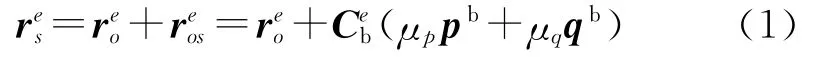
则再入系统质心S的绝对加速度为
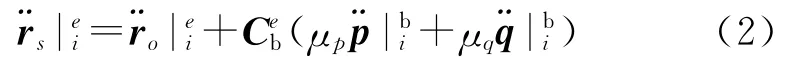
根据牛顿第二定律,可得:

又由于:

根据式(2)~式(4),可得平动动力学方程:

2.2 转动动力学
考虑质量滑块及SGCMG的影响,可写出再入系统相对质心S的总动量矩:


由动量矩定理,可得:

将式(7)代入式(8),可得转动动力学方程为

式中,

如定义SGCMG产生的力矩为
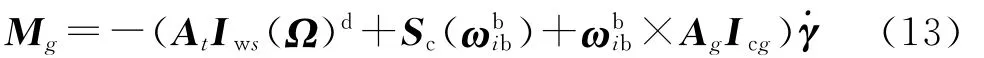
定义质量滑块产生的惯性力矩为
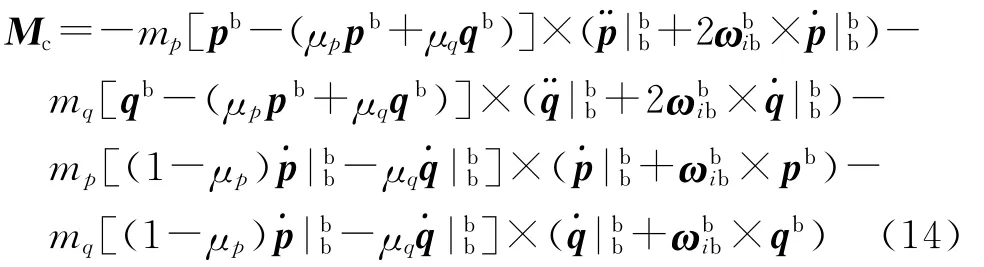
定义质量滑块运动引起的附加转动惯量为

则J=Jo+Jcmg+ΔJ,式(9)可简化为
式中,控制力矩为Ms+Mg,由质量滑块和SGCMG共同产生.
2.3 姿态运动学
在此采用四元数λ=(λ0λ1λ2λ3)T描述弹头相对e系的姿态,记=(λ1λ2λ3)T,则姿态运动学可表示为
如用Euler角表示姿态,滚转角φ、俯仰角θ、偏航角ψ与四元数λ之间可以相互转换,具体转换关系略.
3 非线性姿态控制器设计
为实现弹体对期望姿态的稳定跟踪,必须设计弹头姿态控制器.设弹头目标姿态四元数为λz,当前姿态相对于期望姿态的误差四元数为=(λer0)T,则可写出误差姿态运动学方程为
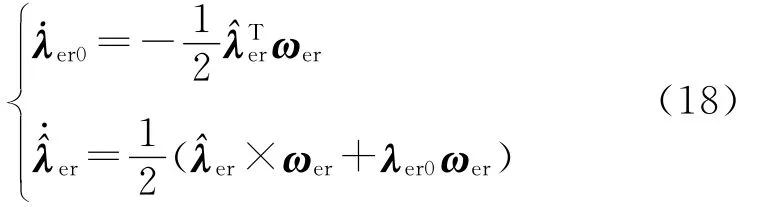
如定义误差角速度为

则可取Lyapunov候选函数为
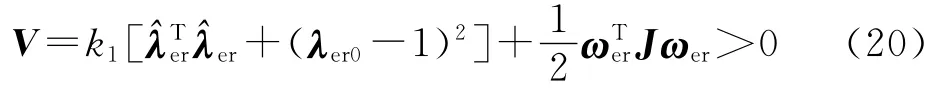
式中,常数k1>0.对上式两端求导,并将式(19)、式(20)、式(16)依次代入,整理可得:
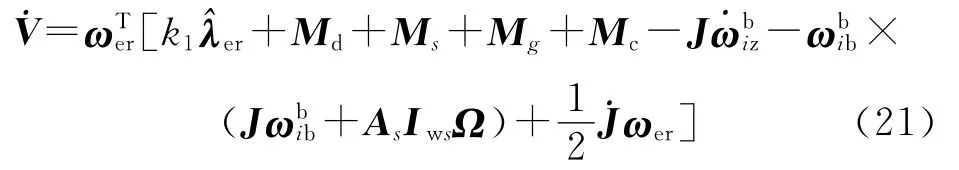
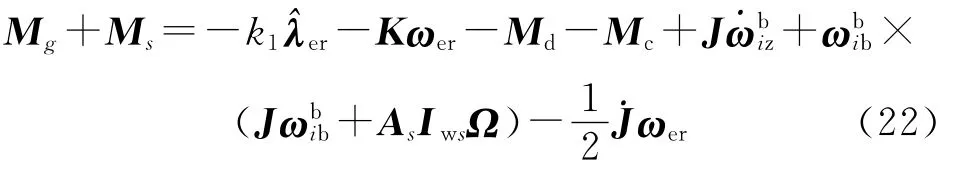
式中,常数矩阵K>0.则式(21)可变为
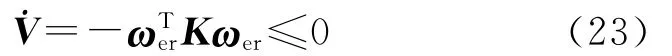
根据Lyapunov稳定性定理和LaSalle不变集定理,可以证明,当t→∞时,ωer→0,er→0,λer0→1,可以实现对期望姿态的稳定跟踪.
如取质量滑块/SGCMG产生的控制力矩为
4 仿真结果与分析
为验证复合执行机构在再入弹头中应用的可行性,在此针对某型弹道导弹的再入弹头进行仿真研究.在仿真中,暂不考虑制导环节的影响,弹头在从一定高度自由下落的过程中,给定指令姿态角,考察弹头姿态控制系统对期望姿态的跟踪能力及复合执行机构的力矩产生能力.
仿真中所用的弹头参数为[8]:弹头质量m=600kg,Jo=diag(55.1,100,100)(kg·m2),初始速度为2km/s,截面积为0.5m2;质量滑块采用导轨平行于弹体坐标系坐标轴的布局,pb=(0py0),qb=(00qz),mp=mq=60kg;考虑到质量和体积限制,采用4个SGCMG,以双平行构型安装,初始框架角为(45 -45 45 -45)T(°),Iws=diag(0.5,0.5,0.5,0.5)(kg·m2),Ict=Icg=diag(0.03,0.03,0.03,0.03)(kg·m2),Ics=diag(0.05,0.05,0.05,0.05)(kg·m2),框架轴安装角为90°,转子角速度Ω=(10 000,10 000,10 000,10 000)T(r/min).假设质量滑块的最大移动距离为0.2m,初始高度为32km.
采用式(22)对再入弹头姿态进行控制,并取k1=3.8,K=diag(8.9,7.9,8.1).由于式(22)给出的期望控制力矩是由质量滑块和SGCMG共同产生的,因此还必须采用一定的控制分配策略,将期望控制力矩分配给质量滑块和SGCMG.在此,采用质量滑块最大使能的控制分配方案,即在控制分配中,优先考虑质量滑块,在质量滑块产生的力矩不能满足需求时,再由SGCMG弥补其不足.对于复合执行机构控制分配方案,将另文详述.在力矩分配的基础上,采用带零运动的伪逆操纵律,将SGCMG的力矩指令分解为框架角速度指令;对式(12)求解,将质量滑块的力矩指令分解为滑块的位置指令.
用φd、θd、ψd表示期望姿态角,Mer表示输出力矩误差,D和hg分别表示SGCMG的奇异测度、总角动量,仿照文献[9]:

可得仿真结果,如图3~图11所示,其中三轴分量均是在体坐标系中.由图3、图4可以看出,在采用SGCMG和质量滑块复合执行机构的情况下,再入弹头姿态控制系统可以实现三轴姿态的良好跟踪,姿态角跟踪误差小于0.5°,姿态角速度误差小于0.01rad/s.由图5则可以看出,复合执行机构能够产生所需的控制力矩,偏航和俯仰力矩误差小于0.000 3N·m,滚转力矩误差小于0.001 5N·m.
图6~图8反映了弹头再入过程中质量滑块的工作情况.可以看出,在弹头再入初始段,由于大气密度较低,滑块不足以产生所需的控制力矩,经常位于最大位置0.2m处,即滑块处于最大使能状态.随着弹头高度不断降低,大气密度不断增加,气动力也随之增大,滑块产生的偏航及俯仰力矩逐步可以满足控制需求.因此,在30s之后,滑块的运动幅值开始不断减小.
图9~图11则反映了弹头再入过程中SGCMG的工作情况.可以看出,在弹头再入的全过程中,滚转力矩主要依赖SGCMG产生,而SGCMG产生的俯仰和偏航力矩则随着弹头高度的降低逐渐减小.同时,SGCMG奇异测度较大,没有出现奇异现象.SGCMG的总角动量小于100N·m·s,远没有达到SGCMG所能提供的最大角动量,不需要卸载操作,工程上是可以实现的.
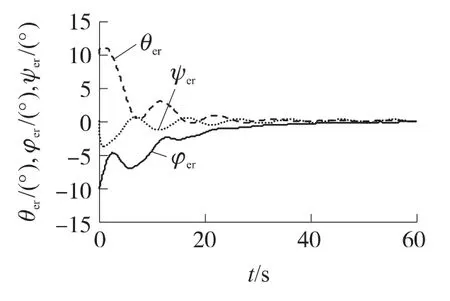
图3 姿态角跟踪误差曲线

图4姿态角速度跟踪误差曲线
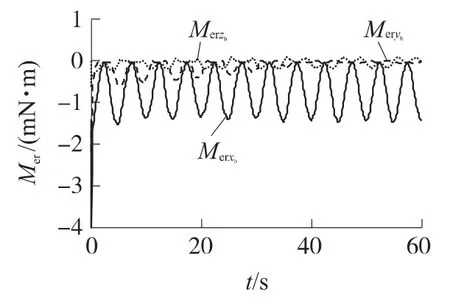
图5控制力矩输出误差曲线

图6 高度变化曲线

图7 质量滑块力矩输出曲线
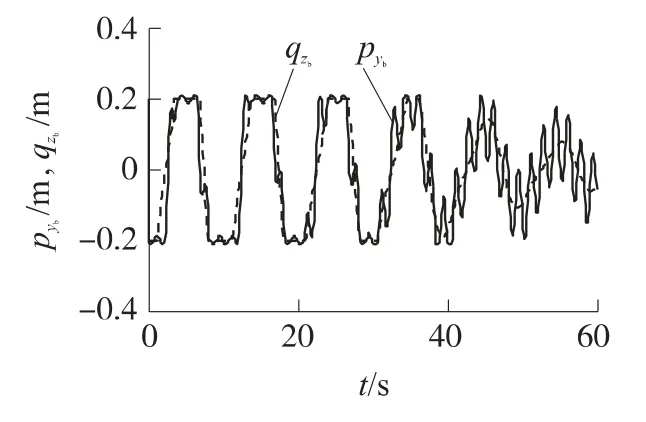
图8 质量滑块位置曲线
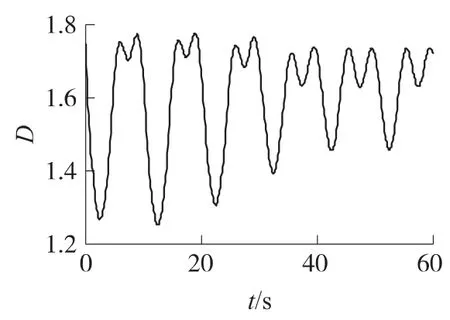
图9 SGCMG奇异测度曲线
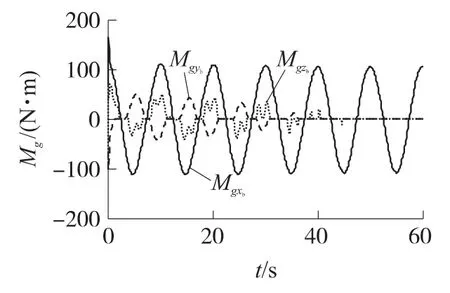
图10 SGCMG力矩输出曲线
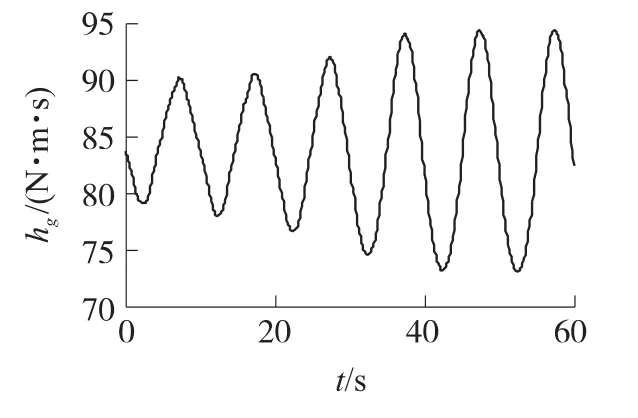
图11 SGCMG总角动量曲线
综合以上分析可知,在弹头再入全过程中,质量滑块和SGCMG组成的复合执行机构可以满足再入过程的控制力矩需求,实现弹头姿态的良好跟踪.当大气比较稀薄时,质量滑块产生的力矩较小,不能满足控制需求,需要SGCMG配合以弥补质量滑块力矩产生能力的不足;当大气比较稠密时,质量滑块可以产生足够大的俯仰及偏航力矩,但在滚转通道仍需SGCMG辅助.
5 结论
本文针对采用质量滑块和SGCMG作为姿态控制执行机构的再入弹头,建立了再入动力学模型,利用Lyapunov稳定性理论,设计了基于复合执行机构的再入弹头非线性姿态控制系统.仿真结果表明:质量滑块/SGCMG复合执行机构能够满足再入弹头姿态控制的力矩需求,实现弹头姿态的良好跟踪,复合执行机构方案是可行的.
[1]MENON P K,SWERIDUK G D,OHLMEYER E J,et al.Integrated guidance and control of moving mass actuated kinetic warheads[J].Journal of Guidance,Control,and Dynamics,2004,27(1):118-126.
[2]高长生,李君龙,荆武兴,等.导弹质量矩控制技术发展综述[J].宇航学报,2010,31(2):307-314.GAO Chang-sheng,LI Jun-long,JING Wu-xing,et al.Key technique and development for moving mass actuated kinetic missile[J].Journal of Astronautics,2010,31(2):307-314.(in Chinese)
[3]MENON P K,VADDI S S,OHLMEYER E J.Finite-horizon robust integrated guidance-control of a moving-mass actuated kinetic warhead[C].Proceedings of 2006 AIAA Guidance,Navigation,and Control Conference.New York:AIAA,2006:6 787-6 799.
[4]VADDI S S,MENON P K,SWERIDUK G D.Multistepping approach to finite-interval missile integrated control[J].Journal of Guidance,Control and Dynamics,2006,29(4):1 015-1 019.
[5]ROGERS J,COSTELLO M.Control authority of a projectile equipped with a controllable internal translating mass[J].Journal of Guidance,Control,and Dynamics,2008,31(5):1 323-1 333.
[6]吴忠,朱挺,魏孔明.基于控制力矩陀螺的再入弹头姿态控制技术研究[C].第29届中国控制会议论文集.北京:北京航空航天大学出版社,2010:6 139-6 142.WU Zhong,ZHU Ting,WEI Kong-ming.On attitude control technology of reentry warhead using control moment gyroscopes[C].Proceedings of the 29th Chinese Control Conference.Beijing:Beijing University of Aeronautics and Astronautics Press,2010:6 139-6 142.(in Chinese)
[7]CUI Nai-gang,FU Yu,GUO Ji-feng,et al.Research on arrival time internal control of multiple independent reentry vehicle[C].Proceedings of the 2009IEEE International Conference on Mechatronics and Automation.New York:IEEE,2009:1 385-1 389.
[8]高长生,荆武兴,于本水,等.质量矩导弹构型及自适应控制律设计[J].航空学报,2010,31(8):1 593-1 599.GAO Chang-sheng,JING Wu-xing,YU Ben-shui,et al.Configuration and adaptive control law design for a mass moment missile[J].Acta Aeronautica et Astronautica Sinica,2010,31(8):1 593-1 599.(in Chinese)
[9]雍恩米,唐金国.一种利用动量轮的弹头姿态控制系统概念研究[J].宇航学报,2006,27(3):396-401.YONG En-mi,TANG Jin-guo.The conceptional study of using moment wheels for the attitude control of a warhead[J].Journal of Astronautics,2006,27(3):396-401.(in Chinese)
[10]TAKEHIRO H,SEIYA U,TAKUYA O.Singularity aviodance steering logic for SGCMG systems using state feedback[C].Proceedings of 2010AIAA/AAS Astrodynamics Specialist Conference.New York:AIAA,2010:8 379-8 391.
