临近空间飞行器滑模控制中的指令参数化方法
2012-12-25刘鲁华
王 鹏,刘鲁华,吴 杰
(国防科学技术大学 航天与材料工程学院,长沙410073)
临近空间飞行器飞行空域、速度的跨度和变化都非常大,体现出快时变、强耦合、强非线性和强不确定的特点,因此对这类对象的控制,传统增益预置的线性控制方法难以达到满意的控制效果,且还会带来分段过多、控制器频繁切换的问题,而非线性控制方法则提供了更好的解决方案[1~7].
非线性动态逆控制又称为反馈线性化方法,是上世纪90年代,SNELL、ENNS和GARRARD等人针对飞机在做大迎角超机动飞行时的本体非线性、强耦合特征而提出来的非线性控制策略[1],其基本思想是:对于具体的研究对象,用系统模型生成一种可用反馈方法实现的原系统的“α阶积分逆系统”,将对象补偿为具有线性传递关系的伪线性系统.滑模变结构控制的结构在动态过程中根据系统当前的状态(如偏差及其各阶导数等)有目的地不断变化,迫使系统按照预定“滑动模态”的状态轨迹运动[8],因此滑模变结构控制对参数偏差和外界干扰具有较强的鲁棒性.
本文将动态逆方法的线性化能力与滑模控制的强鲁棒性有机结合,设计了临近空间飞行器纵向滑模控制系统,并从提高信息利用率和增加控制系统设计自由度的角度出发,提出俯仰角变化率指令参数化计算方法,通过仿真计算分析了指令参数对控制效果的影响.
1 临近空间飞行器纵向模型
临近空间飞行器无动力平稳滑翔阶段的侧向运动参数变化较小,本文主要针对其纵向运动开展姿态控制问题研究.为了推导面向控制的纵向运动模型,提出如下假设:①视地球为均质圆球,并忽略地球旋转;②飞行器为面对称体,惯量积Jxz=Jyz=0,惯量积Jxy为小量,忽略不计;③侧向运动参数z,β,σ,γV,ψ,γ,ωx,ωy均为小量.
基于上述假设,得到飞行器面向控制的标量形式纵向运动模型为

式中,v为飞行器速度;θ为速度倾角;ωz为俯仰角速度;x,y为飞行器在地面坐标系中的位置坐标;φ为俯仰角;地球引力常数μ=3.986×1014m3/s2;地心距,Re为球形引力场时的地球平均半径;FD,FL分别为阻力和升力;Mz为俯仰力矩;m为飞行器质量;Jz为飞行器z轴转动惯量.
攻角α与俯仰角、速度倾角之间满足如下关系:

阻力、升力和俯仰力矩的表达式分别为

式中,动压q=ρv2/2,ρ为空气密度;Se为飞行器参考面积;l为飞行器参考长度;CD、CL为阻力系数和升力系数;mz为俯仰力矩系数.
气动力系数和力矩系数是飞行马赫数Ma、高度H、攻角α及俯仰舵偏角δφ的非线性函数,可表示为

2 模型的可逆性分析
状态变量取为

输入量取为俯仰舵偏角,即u=δφ,输出量取为飞行器俯仰角,即Y=φ,则飞行器纵向运动模型可表述为

式中,

纵向动力学模型是一个SISO(单输入单输出)系统.为了分析飞行器运动模型的可逆性,给出MIMO(多输入多输出)非线性系统的可逆性定理——函数可控性定理.
定理1[9]一般 MIMO 非线性系统在(X0,u0)的邻域内可逆的充分必要条件是在此邻域内存在相对向量阶,即(X0,u0)为Interactor算法的正则点.
SISO系统是MIMO系统的特殊情况,故式(6)所示的SISO系统在(X0,u0)的某个邻域内可逆的充分必要条件是在此邻域内存在相对阶k.求解系统相对阶的基本方法是Interactor算法[9].该算法的基本思想是:输出的每个分量分别对时间求导数,直到导数中显含输入量为止,所求导数的次数即为该分量的相对阶.
经过推导可得:

俯仰角二阶导数对控制量u的偏导数为

对于临近空间滑翔飞行器而言,ρ、v、Se、l均不为0,而mz为俯仰舵偏角δφ的函数,因此不始终为0,故不恒等于0,即俯仰角二阶导数中已显含控制量.
Interactor算法正常结束,相对阶k=2,小于系统阶数n=6,故飞行器纵向运动模型是可逆的.而推导中仅用到了绕质心的运动方程,相对阶等于绕质心运动模型的系统阶数,因此动态逆方法可实现绕质心运动模型的线性化.
3 基于指令参数化的纵向滑模控制器设计
飞行器纵向运动模型逆系统的输入为俯仰角的二阶导数,为了将滑模变结构控制与逆系统结合起来,在控制系统设计时滑模面应包含姿态角的一阶导数,这样,滑动函数仅需计算一次导数即可含有输入量.为此可取滑动函数为[10]

式中,λ为正常数,跟踪误差e=φ-φc,φc为俯仰角指令.
为了能够使S达到0,即能够使系统轨迹在有限时间内到达滑动面,需为非线性系统选择适当的控制律,满足如下的滑动条件:

取Lyapunov函数为

则其对时间的微分为=,滑动条件已保证<0,故<0,即系统是稳定的.可见滑动条件与系统稳定性是等价的.
为了使式(10)成立,根据趋近律设计思想,可以选取如下的等速趋近律:

式中,ε为可选的严格正常数,sign(·)表示符号函数.
对式(9)微分得:

将式(12)代入上式得:

为了抑制抖振,将上式中的符号函数sign(S)用饱和函数sat(S,d)代替,饱和函数的定义为[10]

式中,d为可选的正常数.
于是控制律变为
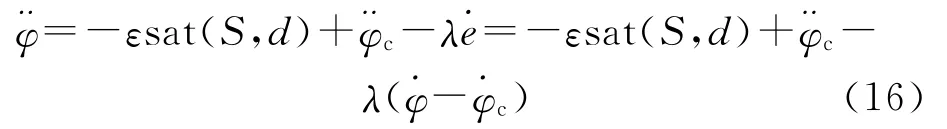
纵向滑模控制系统结构如图1所示.

图1 纵向滑模控制系统结构图
纵向控制系统的输出为俯仰角,故最直接的控制方式是跟踪俯仰角指令,而实际中控制指令一般以攻角形式给出.俯仰角和攻角可由欧拉角关系式(2)相互转化,只需将攻角指令与当前时刻速度倾角相加即可得到俯仰角指令φc=αc+θ,故2种控制指令本质上是一致的.
式(16)所示的滑模控制律中用到俯仰角一阶导数指令c和二阶导数指令,其中一阶导数指令对控制系统的指令跟踪性能影响较大.按照常规控制系统设计方法,俯仰角一阶导数指令由俯仰角指令对时间求导数直接得到,即

这种方法直观、易理解,被广泛采用.但若将c理解为俯仰角一阶导数期望值,则最理想的状况为

式中,φ为俯仰角实际值,Δt为仿真时间步长,经过一个控制步长,俯仰角就可以达到期望值φc.按照这样的思路,式(17)所示常规计算方法的隐含前提是控制系统已将跟踪误差控制在较小范围内,此时俯仰角指令与实际值相差不大,俯仰角一阶导数期望值与俯仰角指令一阶导数基本相同,因此常规方法比较适用于跟踪误差较小的情况.当跟踪误差较大时,常规方法的控制性能会明显变差.另外从形式上看,常规计算方法只用到了俯仰角指令值,而未考虑俯仰角实际值,对信息的利用率不高.
本文从充分利用已有信息和增加控制系统设计自由度的角度出发,同时考虑到控制系统的延迟、超调等实际动态特性,对式(18)进行适当改造,提出参数化的俯仰角变化率(一阶导数)指令计算方法,即

式中,Kω为俯仰角变化率指令参数.上式中所用数据包括φc、φ、Δt和Kω,其中前3个量是已知的或可测量的,在控制律式(16)中已用到了俯仰角及其指令值,在此又用其构造俯仰角一阶导数指令,提高了已有信息的利用率;而俯仰角变化率指令参数Kω是引入的一个全新控制参数,增加了控制系统设计的自由度.该方法不仅适用于俯仰角实际值与指令值偏差不大的情况,对于偏差较大的情况也有较好的适应能力,通过调节指令参数,可有效提高控制系统的动态响应能力和稳态控制精度.
4 控制系统仿真分析
仿真初始条件如表1所示.

表1 仿真初始条件
俯仰角变化率指令参数Kω对控制系统动态响应影响较大,特别是在控制指令出现较大变化时影响尤为突出.由于初始误差和指令突变的影响,在初始时刻和900s附近存在较大的跟踪误差,故这两个时刻是特征控制点.Kω取不同值时,攻角跟踪误差如表2所示.表中,emax、ξ分别为特征控制点附近的攻角最大跟踪误差和超调量;eme1、eme2分别为控制全过程的攻角平均跟踪误差和平均绝对跟踪误差.

表2 不同指令参数条件下的跟踪误差
取λ=2,ε=0.2,d=0.05,仿真步长100ms,攻角指令及部分仿真结果如图2~图4所示.由表2和图2可知:基于指令参数化的纵向滑模控制系统可以准确跟踪攻角指令,在不同指令参数条件下,攻角最大跟踪误差为3°左右,平均跟踪误差eme1和平均绝对跟踪误差eme2均小于0.03°.

图2 攻角指令及其跟踪误差

图3 攻角跟踪误差局部放大图
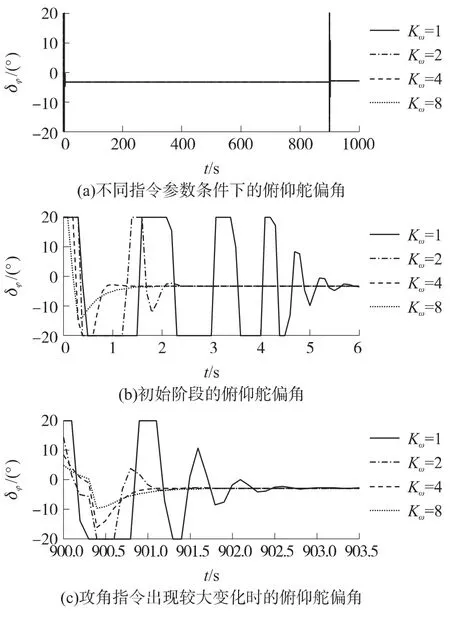
图4 俯仰舵转角及其局部放大图
由表2、图3、图4可知,指令参数Kω对控制精度影响较大.当Kω较小时,特征控制点处的emax和ξ均较大,而eme1和eme2较小.由式(18)可知,俯仰角变化率指令与Kω值成反比,Kω较小时,俯仰角变化率指令较大,即控制系统动态响应能力强,相同跟踪误差条件下,控制输入较大,故存在较大超调量.Kω值越小,图3中所示超调量越大,图4中俯仰舵偏角维持在最大值的时间越长,都说明了这一点.随着Kω值的增大,emax先减小再增大;ξ不断减小,即控制系统的动态响应能力不断下降;eme1、eme2不断增大,且二者相对差越来越小,即控制系统的稳态精度不断变差.为了保证控制系统同时具有良好的动态响应能力和稳态精度,Kω值不应过大或过小,应根据实际需要进行折中处理.
5 结束语
临近空间飞行器纵向运动模型是可逆的,且相对阶数等于绕质心运动模型的系统阶数,故动态逆方法可实现绕质心运动模型的线性化.
由内环动态逆控制器和外环滑模控制器所组成的飞行器纵向控制系统可以准确跟踪攻角指令.指令参数Kω越小,控制系统动态响应能力越强,但会带来超调量过大的问题;该参数值越大,控制系统稳态精度越差.因此,为了保证控制系统同时具有良好的动态响应能力和稳态精度,Kω值应进行折中处理.
[1]SNELL S A,ENNS D F,GARRARD L.Nonlinear inversion flight control for a super maneuverable aircraft[J].Journal of Guidance,Control,and Dynamics,1992,15(4):976-984.
[2]WANG Q,STENGEL R F.Robust nonlinear control of a hypersonic aircraft[J].Journal of Guidance,Control,and Dynamics,2000,23(4):577-585.
[3]刘燕斌,陆宇平.非线性动态逆控制在高超飞控系统中的应用[J].应用科学学报,2006,24(6):613-617.LIU Yan-bin,LU Yu-ping.Application of nonlinear dynamic inversion control in flight control of hypersonic vehicle[J].Journal of Application Sciences,2006,24(6):613-617.(in Chinese)
[4]LEE H P,REIMAN S E,DILLON C H.Robust nonlinear dynamic inversion control for a hypersonic cruise vehicle,AIAA 2007-6685[R].2007.
[5]KEUM W L,SUBRAMANIAN R,SAHJENDRA N S.Adaptive sliding mode 3-D trajectory control of F/A-18 model via SDU decomposition,AIAA 2008-6460[R].2008.
[6]LI H F,SUN W C,LI Z Y,et al.Index approach law based sliding control for a hypersonic aircraft,AIAA 2009-1734[R].2009.
[7]XU H J,MIRMIRANI M D,IOANNOU P A.Adaptive sliding mode control design for a hypersonic flight vehicle[J].Journal of Guidance,Control and Dynamics,2004,27(5):829-838.
[8]刘金琨,孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用,2007,24(3):407-418.LIU Jin-kun,SUN Fu-chun.Research and development on theory and algorithms of sliding mode control[J].Control Theory& Applications,2007,24(3):407-418.(in Chinese)
[9]戴先中.多变量非线性系统的神经网络逆控制方法[M].北京:科学出版社,2005.DAI Xian-zhong.Neural network inverse control method for multivariable nonlinear system[M].Beijing:Science Press,2005.(in Chinese)
[10]刘燕斌,陆宇平.基于变结构理论的高超音速飞机纵向逆飞行控制[J].信息与控制,2006,35(3):388-392.LIU Yan-bin,LU Yu-ping.Longitudinal inversion flight control based on variable structure theory for hypersonic vehicle[J].Information and Control,2006,35(3):388-392.(in Chinese)
