铝合金－聚合物复合层板弯曲回弹理论分析

刘建光，刘 伟，薛 卫

(1.哈尔滨工业大学金属精密热加工国家级重点实验室，哈尔滨150001，E-mail:liujg@hit.edu.cn;

2.哈尔滨工业大学材料科学与工程学院，哈尔滨150001;3.四川成发航空科技股份有限公司技术中心，成都610503)

铝合金－聚合物复合层板弯曲回弹理论分析

刘建光1，2，刘 伟1，2，薛 卫2，3

(1.哈尔滨工业大学金属精密热加工国家级重点实验室，哈尔滨150001，E-mail:liujg@hit.edu.cn;

2.哈尔滨工业大学材料科学与工程学院，哈尔滨150001;3.四川成发航空科技股份有限公司技术中心，成都610503)

针对铝合金-聚合物复合层板弯曲回弹问题，分析了复合层板弯曲过程表面层铝板及中心层聚合物的变形特征，建立了复合层板平面应变纯弯曲回弹理论分析模型.采用建立的模型预测了复合层板纯弯曲过程回弹角变化，并与实验结果进行了对比，分析了聚合物层厚度及铝合金板材力学性能对回弹的影响规律.结果表明:随着中心聚合物层厚度的增加，复合层板回弹角降低;随着表面层铝板强度的降低，复合层板回弹角减小.理论预测结果与实验结果一致，说明了本文推导的理论模型的可靠性.

复合层板;纯弯曲;回弹;理论分析;铝合金

近年来，在汽车、航空、航天等领域，为了实现结构减重，开始大量采用轻质材料和轻质结构.其中，采用两层金属板材夹一层聚合物结构的金属-聚合物复合层板作为一种新型的轻质结构材料逐渐得到应用［1-2］.与单一层金属板材相比，金属-聚合物复合层板具有较低的密度、较高的比弯曲刚度、良好的减震和降低噪音的作用、较高的静态抗凹性及良好的疲劳性能［3］.钢-聚合物复合层板作为第一代复合层板，已经得到了广泛的关注和应用.尤其在汽车领域，钢-聚合物复合层板已成功用于制造汽车发动机油箱底壳、摇臂罩、发动机隔板、发动机罩、齿轮罩等部件［4］.铝合金-聚合物复合层板作为第二代复合层板，较钢-聚合物复合层板具有更加显著的减重、降噪等特性，近年来受到了越来越多的关注，已成功用于汽车发动机罩盖等零件的成形［5］.

金属-聚合物复合层板具有多层非均质结构的特点，因此，弯曲成形过程要比单一层金属板材复杂.近年来，国内外学者针对复合层板弯曲回弹问题开展了部分研究工作.Huang等［6］采用有限元分析方法预测了钢-聚合物复合层板弯曲过程产生的“反弯曲”现象，并通过分析层间剪切力变形进行了解释.Corona等［7］对钢-聚合物复合层板窄条折弯过程进行了实验和数值模拟，研究了钢板屈服应力、厚度及中心层聚合物剪切模量等因素对复合层板弯曲回弹的影响规律.Ito等［8］采用Von Mises屈服准则线性强化材料模型描述复合层板面板，建立了复合层板弯曲回弹理论模型.实际上，面板通常具有较强的各向异性，其屈服条件采用各向异性屈服准则更为合适［9］.

本文针对铝合金-聚合物复合层板纯弯曲回弹问题，分析了不同结构复合层板弯曲过程面板及中心层聚合物的变形特征，采用Hill屈服准则和指数强化模型描述各向异性铝合金面板，建立了复合层板平面应变纯弯曲回弹的理论分析模型.采用建立的模型预测了铝合金-聚乙烯复合层板纯弯曲回弹角，并与实验结果进行了对比，分析了聚合物层厚度及铝合金板材力学性能对回弹的影响规律.

1 复合层板纯弯曲回弹分析模型

图1为复合层板结构示意图，由两层金属板材夹一层聚合物粘接而成.复合层板的弹性模量和泊松比可以通过表面层金属板材和中心聚合物材料的弹性模量和泊松比“复合”而成［5］，

式中:Es、μs和ts分别为复合层板的弹性模量、泊松比及厚度，Ef、μf和tf分别为表面层金属板材的弹性模量、泊松比及厚度，Ec、μc和tc分别为中心聚合物的弹性模量、泊松比及厚度.

图1 复合层板结构示意图

复合层板弯曲示意图如图2所示，图中Ri、Ro分别为复合层板弯曲内径和外径，Rn为中性层曲率半径，Rc为中面层半径，θ为弯曲角.为了便于理论分析复合层板的弯曲过程，本文做如下假设［10］.

1)复合层板弯曲时变形处于平面应变状态，即板料在宽度方向上应变εz为零;

2)复合层板弯曲变形服从Kirchhoff假设;

3)复合层板弯曲过程中，圆角处各层板料之间无挤压，即认为复合层板厚向应力σr为零，且忽略板厚的变化.

4)忽略表层铝合金板材变形的“包申格”效应.

下面分别详细推导复合层板弯曲横截面应力及弯矩.

图2 复合层板弯曲示意图

1.1 复合层板横截面应力计算

图3为复合层板弯曲横截面应力及应变分布图.图中，h为中性层距中心层与外层铝板界面的距离;h1为外层铝板弹性变形区宽度，h2为内层铝板弹性变形区宽度.

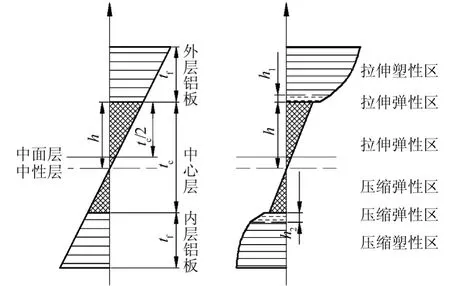
图3 复合层板弯曲应力－应变分布图

根据Kirchhoff假设，对于复合层板弯曲截面任意曲率半径为R的一点，其长度方向的线应变为

由于复合层板弯曲过程中心层聚合物的变形通常比较小，且由于聚合物的弹性变形能力相对于表层铝板大的多，因此，在推导复合层板弯曲回弹模型时，只考虑中心层聚合物的弹性变形，且符合胡克定律.因此，对于处于平面应变状态弹性变形的铝合金板材及聚合物，横向应力可表示为

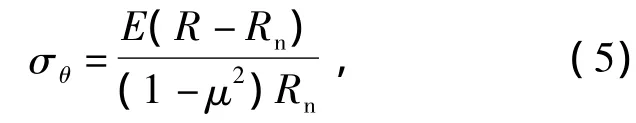
式中:σθ为切向应力(MPa).

弯曲过程中，内、外层铝板可能发生弹性变形、弹塑性变形或塑性变形3种情况.这主要取决于中心层聚合物的厚度及表层铝板的屈服强度.当复合层板厚度较薄且弯曲半径较大，内外表层铝板均仅发生弹性变形时，卸载后弯曲角将得到完全恢复，这种情况不需计算回弹角.当复合层板厚度较厚，且弯曲半径较小时，表层铝板将部分或完全发生塑性变形，卸载后弯曲角发生部分回弹.此种情况下，若中心层聚合物较厚，表层铝板将完全发生塑性变形;若中心层聚合物较薄(例如减震板)，表层铝板可能存在部分发生塑性变形的情况.

当表层铝板进入塑性变形区后，横向应力服从Hill厚向异性屈服准则，屈服方程为

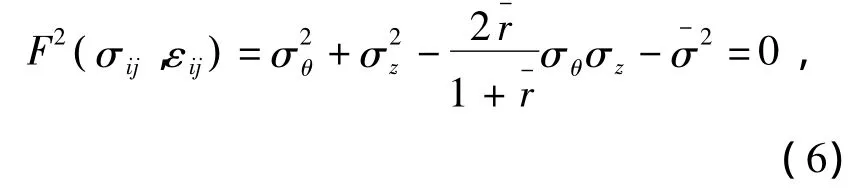
式中:σ-为流动应力(MPa);σz为宽度方向上的应力(MPa);r-为板料厚向异性参数.

在塑性变形区内，由于宽度方向应变为零，则

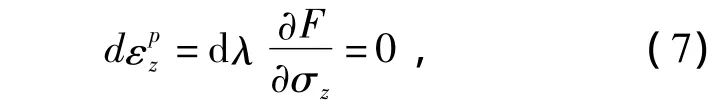
式中:dλ为正的待定有限量，它的数值和材料硬化指数法则有关.

与式(6)相关联得到

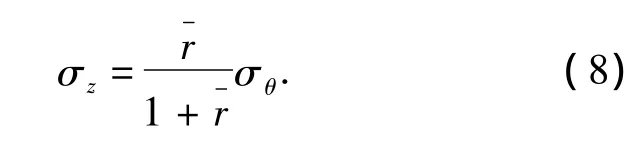
将式(8)带入到式(6)，可得

设表层铝板在塑性区内服从指数应力应变硬化关系，

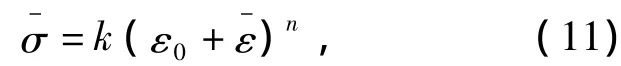
式中:ε-为等效塑性应变;K为强度系数;n为硬化指数;ε0为板料的初始应变.

将式(9)、(10)代入式(11)，得到进入塑性区表层铝合金板材的横向应力表达式

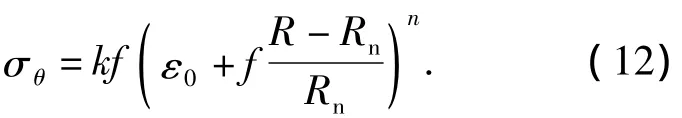
1.2 弯曲过程横截面弯矩推导

复合层板弯曲过程，横截面弯矩包括内层铝板弯矩、中心层聚合物弯矩及外层铝板弯矩3部分，

式中:Ms为复合层板弯曲总弯矩;Mif为内层铝板弯矩;Mc为中心层聚合物弯矩;Mof为外层铝板弯矩.

由于复合层板弯曲过程中，中性层的位置靠近内表面，内外面板的弯曲变形并不对称.各部分弯矩推导过程中，以中性层距外层铝板界面的距离h代替中性层的位置.下面将分别推导各部分的弯矩.

1)中心层聚合物弯矩

中心层聚合物弯矩可根据横截面弹性应力计算而得

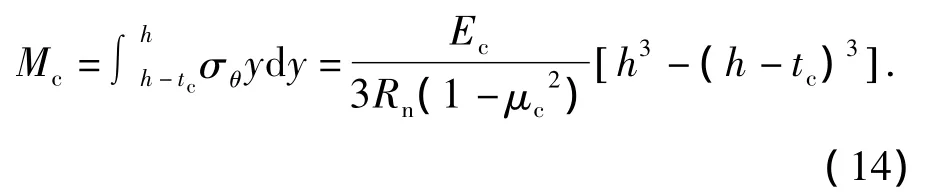
2)表层铝板弯矩

表面层铝板均按发生弹塑性变形方式进行推导.

外层铝板弯矩表示为

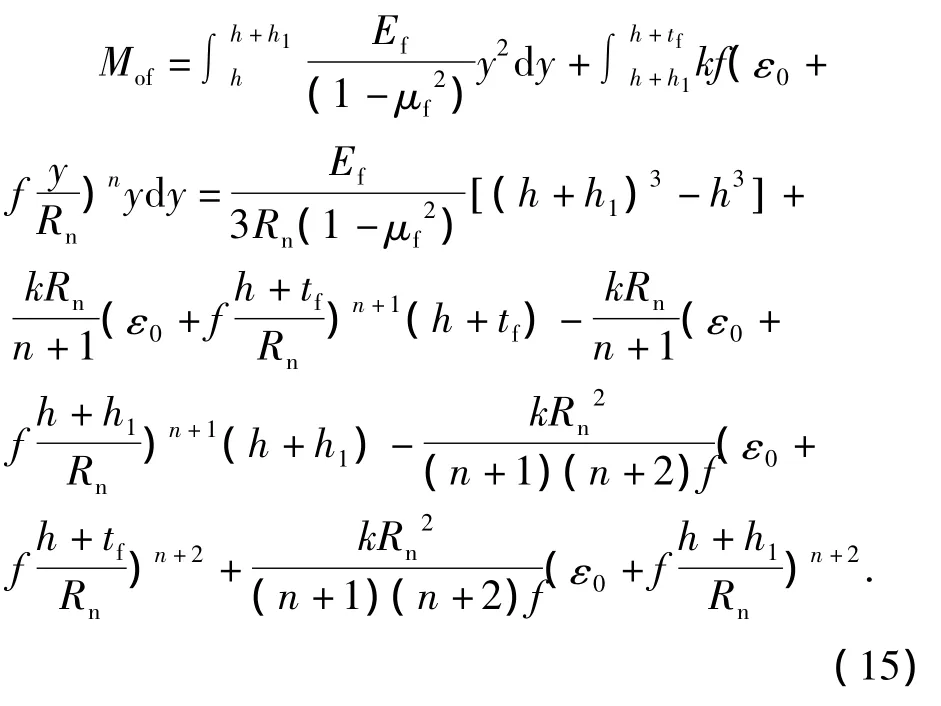
内层铝板弯矩表示为

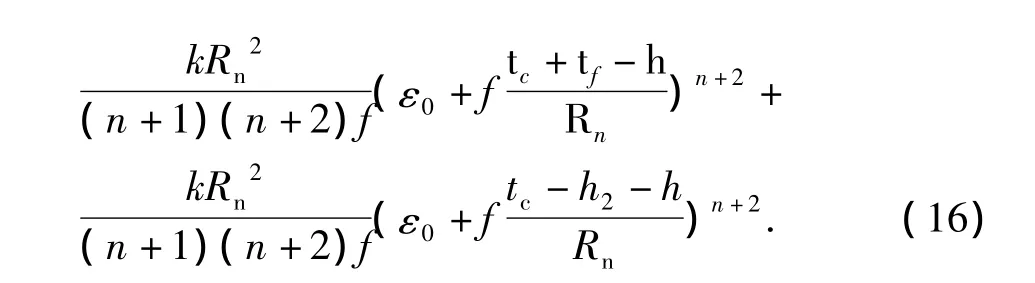
下面分别对内外层铝板变形弯矩进行讨论.

1)当h1=0时，外层铝板弯矩公式中的第1项积分后为零，即外层铝板完全发生塑性变形，此时的外层铝板弯矩为塑性弯矩;当h1=tf时，外层铝板弯矩公式中的除第1项外的其他项可抵消为零，即外层铝板完全发生弹性变形，此时的外层铝板弯矩为弹性弯矩.

2)同样，对于内层铝板，当h2=0时，外层铝板完全发生塑性变形，内层铝板弯矩为塑性弯矩;当h2=tf时，内层铝板完全发生弹性变形，内层铝板弯矩为弹性弯矩.

经推导得h1和h2可表示为

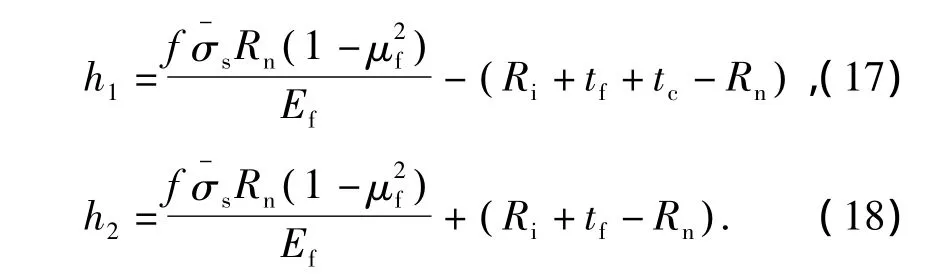
本文建立的模型采用Hill提出的方程计算复合层板弯曲中性层曲率半径［10］

1.3 回弹角计算

在卸载过程中，复合层板内部切向应力的变化势必引起复合层板的形状和尺寸的变化.其主要表现在中性层曲率半径Rn卸载后变为Rn'，角度α卸载后变为α'.由于卸载过程是弹性变形过程，因此，可以利用弹性弯曲时弯矩与曲率变化量之间的公式进行计算，

式中:Is为复合层板单位宽度方向上横截面惯性矩，表示为

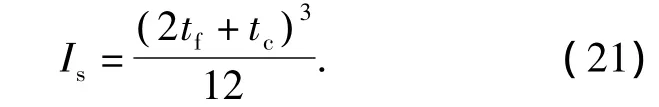
Es'为复合层板在平面应变下的弹性模量，表示为

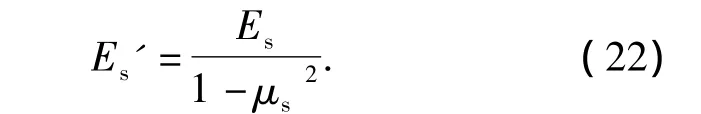
卸载后的复合层板中性层曲率半径为

复合层板卸载前后的两个端面仍保持平面，则可测得复合层板卸载前的弯曲角α与卸载过后的弯曲角α'.复合层板发生的弹性恢复现象时，复合层板的中性层的长度不发生变化，则

根据式(23)、式(24)可求得卸载后的回弹角.

2 铝合金-聚乙烯复合层板回弹分析

为了验证推导的复合层板弯曲回弹理论分析模型，进行了铝合金-聚乙烯复合层板纯弯曲实验.分别选用3种厚度(0.5，1.0和2.0 mm)的聚乙烯作为中心层材料及3种牌号的铝合金(AA2024-T3，AA5052-O和AA1060-O)作为面板制备复合层板，其中，3种铝合金面板壁厚均为0.5 mm.表1为3种铝合金板材力学性能参数，其中，AA2024-T3强度最高，AA1060-O强度最低.采用的中心层材料为高密度聚乙烯，该材料具有宽泛的弹性变形区间，良好的塑性.通过拉伸实验可得其屈服强度为15 MPa，泊松比为0.33，弹性模量为0.5 GPa.制备的复合层板弯曲试样长度为100 mm，宽度为25 mm.复合层板制备过程中，在热压作用下中心层聚乙烯厚度有一定的减小，本文计算过程中，以实测厚度为准.纯弯曲实验在CSS-88050电子拉伸试验机上进行，图4为铝合金-聚乙烯复合层板纯弯曲实验装置，其中冲头圆角半径为17 mm，弯曲速度为3 mm/min，冲头行程25 mm.为了尽量避免实验误差，每组实验进行3次.

表1 3种铝合金板材力学性能参数

图5为弯曲实验得到的试件.从弯曲试件对比可以看出，对于AA2024-聚乙烯复合层板，当中心聚合物层厚度为1.9 mm时，弯曲试件的直壁部分发生了明显的“反弯曲”现象，这是由于聚合物与铝合金界面剪应力作用造成的.随着聚合物层厚度的减小，“反弯曲”角逐渐减小.中心层聚合物厚度为1.5 mm的AA5052-聚乙烯复合层板弯曲过程中也发生了“反弯曲”现象，但与AA2024-聚乙烯复合层板相比，“反弯曲”角较小，且随着聚合物层厚度的降低，“反弯曲”逐渐消失.而3种厚度的AA1060-聚乙烯复合层板弯曲后无明显的“反弯曲”现象发生.本文在建立弯曲回弹理论分析模型过程现中，忽略了“反弯曲”现象对回弹的影响.

图4 复合层板纯弯曲实验装置

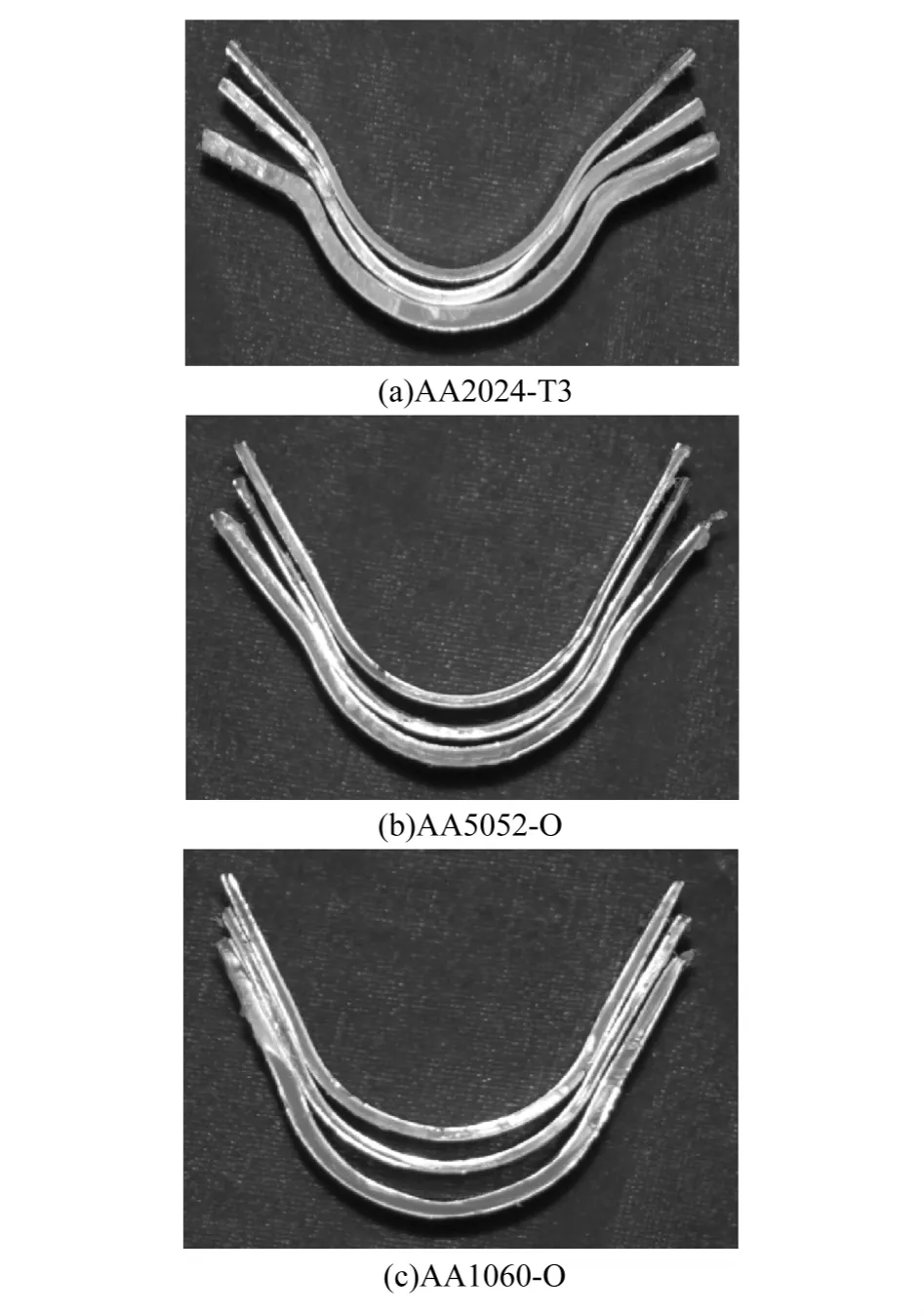
图5 弯曲实验件

采用图6所示的方法测量复合层板弯曲卸载前后的弯曲角度，可得到回弹角.表2对比了理论预测的回弹角与实验测量结果，可以看出，随着复合层板中心聚合物的厚度增加，回弹角降低;随着表面层铝板强度的降低，回弹角减小.从表2还可以看出，理论计算的复合层板弯曲回弹角与实验测量值基本一致，尤其对于厚度为2.5 mm的AA1060-聚乙烯复合层板，理论计算值与实验测量值高度吻合，说明了本文建立的理论分析模型可以较好地预测铝合金-聚合物复合层板弯曲回弹角.

图6 回弹角测量示意图

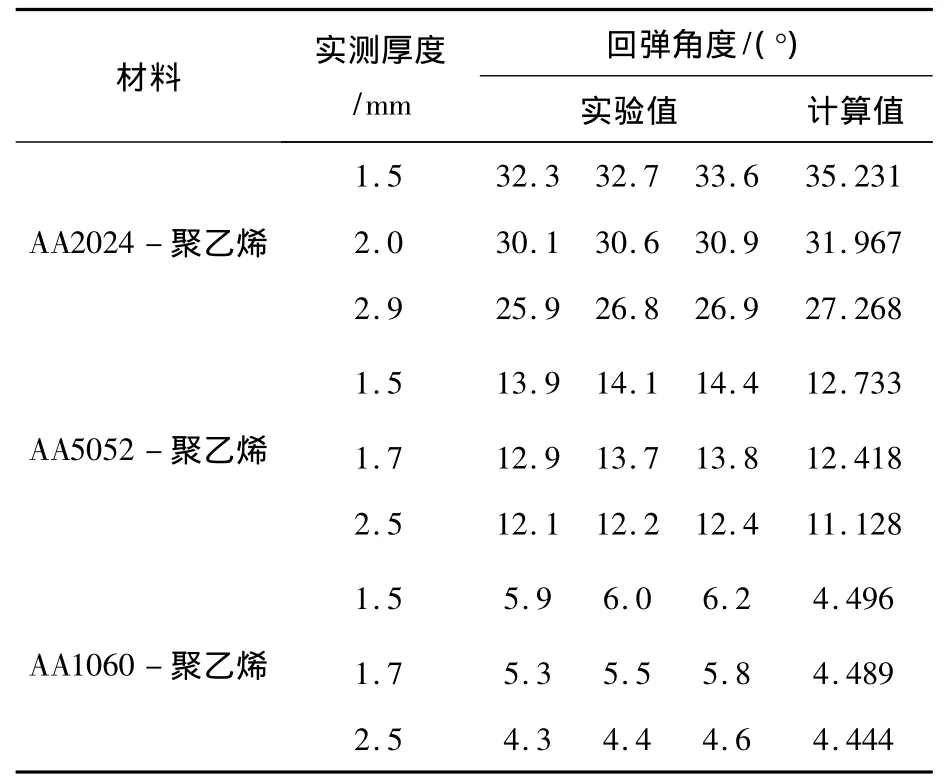
表2 回弹角理论预测与实验结果对比

3 结论

1)分析复合层板弯曲过程面板及中心层聚合物的变形特征，采用Hill屈服准则和指数强化模型描述各向异性铝合金面板，建立了复合层板平面应变纯弯曲回弹的理论分析模型.

2)随着复合层板中心聚合物层厚度的增加，回弹角降低;随着表面层铝板强度的降低，回弹角减小.

3)理论预测结果与实验结果一致，说明本文建立的模型可以较好地预测铝合金-聚合物复合层板弯曲后的回弹角.

［1］ DICELLO，J A.Steel-polypropylene-steel laminate-A new weight reduction material［J］.SAE Paper 800078，19801-15.

［2］ VEENSTRA E W.Aluminum-Plastic-Aluminum sandwich sheet for maximum weight reduction in body panels［J］.SAE paper 930706，19931-10.

［3］ LINK T D.Formability and performance of steel-plastic steel laminated sheet Materials［J］.SAE paper，2001 -01-0079，2001.

［4］ YAO H，CHEN C C，LIU S D，et al.Laminated steel forming modelling techniques and experimental verifications［J］.SAE-2003-01-0689，2003.

［5］ KEE J K，RHEE H M，CHOI B I，et al.Development of application technique of aluminum sandwich sheets for automotive hood［J］.International Journal of Precision Engineering and Manufacturing，2009，10(4):71-75.

［6］ HUANG Y M，LEU D K.Finite-element simulation of the bending process of steel/polymer/steel laminate sheets［J］.Journal of Materials Processing Technology，1995，52(2-4):319-337.

［7］ CORONA E，EISENHOUR T.Wiping die bending of laminated steel［J］.International Journal of Mechanical Sciences，2007，49(3):392-403.

［8］ ITO K，KASAJIMA M，FURUYA S.Bending and springback theory of metal-polymer sandwich laminates［J］.Journal of Macromolecular Science-Physics，1980，B19(4):773-791.

［9］ ZHANG D J，CUI Z S，CHEN Z Y，et al.An analytical model for predicting sheet springback after V-bending［J］.Journal of Zhejiang University-Science A，2007，8 (2):237-244.

［10］ 余同希，章亮炽.塑性弯曲理论及其应用［M］.北京:科学出版社，1992.

Theoretical analysis on springback of aluminum alloy-polymer sandwich sheets in bending process

LIU Jian-guang1，2，LIU Wei1，2，XUE Wei2，3
(1.National Key Laboratory for Precision Hot Processing of Metals，Harbin Institute of Technology，Harbin 150001，China，E-mail:liujg@hit.edu.cn;2.School of Materials Science and Engineering，Harbin Institute of Technology，Harbin 150001，China; 3.Sichuan ChengFa Aero Science＆Technology Co.Ltd Tech-R＆D Center，Chengdu 610503，China)

This paper focus on studying the springback of aluminum alloy-polymer sandwich sheets in bending process.An analytical model for predicting the springback of sandwich sheets was proposed on the basis of analyzing the deformation behavior of skin sheet and core materials in bending process.Then the proposed model was used to predict the springback angle of aluminum alloy-polyethylene sandwich sheets after pure bending process.The predicted results were compared with experimental ones and the influences of the thickness of polymer and mechanical properties of aluminum alloy sheet on the springback angle were investigated.The springback angle of aluminum alloy-polymer sandwich sheet decreases with the increasing of polymer thickness and decreasing of the strength of the aluminum alloy sheet.Good agreements between predicted results and experimental ones prove the validity of the proposed model.

sandwich sheets;bending;springback;theoretical analysis;aluminum alloy

TG386 文献标志码:A 文章编号:1005-0299(2012)01-0114-05

2011-09-05.

哈尔滨工业大学科研创新基金资助项目(HIT.NSRIF.2009033).

刘建光(1979-)，男，博士，讲师.

(编辑 吕雪梅)