三维有限元刚度矩阵的压缩存储算法

王忠雷，赵国群，马新武

(1.山东大学材料液固结构演变与加工教育部重点实验室，济南250061;2.山东建筑大学机电工程学院，济南250101)

三维有限元刚度矩阵的压缩存储算法

王忠雷1，2，赵国群1，马新武1

(1.山东大学材料液固结构演变与加工教育部重点实验室，济南250061;2.山东建筑大学机电工程学院，济南250101)

为提高有限元分析效率、减少存储空间消耗，对刚度矩阵的压缩存储算法进行了研究.研究了“广义相邻节点对”与刚度矩阵中非零子矩阵的关系，确定了刚度矩阵中非零子矩阵的分布规律;提出了一种新的刚度矩阵压缩存储方法—“改进的CSR存储方法”，给出了基于压缩存储的刚度矩阵的生成过程以及线性方程组迭代解法方法，并将提出的算法应用于三维体积成形有限元分析软件.有限元分析实例表明，该算法可以有效地减少存储空间，提高计算效率.

三维有限元方法;刚度矩阵;压缩存储;六面体网格

随着计算机技术和有限元技术的发展，有限元模拟在金属塑性加工中获得了广泛应用，并发挥了不可替代的作用［1-3］.近年来，所要分析的工程问题日益复杂、数据量大，尤其是在大型三维体积成形过程数值分析中，工件形状的复杂性导致单元模型节点数量的激增，从而使得有限元软件在分析该类问题时计算效率低下，甚至在分析大型、超大型问题时出现存储空间不足的情况，这大大限制了有限元软件在大型体积成形分析中的应用.

工程问题的有限元分析最终都归结为求解大型线性方程组，有限元的求解效率在很大程度上取决于线性方程组的解法及刚度矩阵的存储结构.有限元刚度矩阵一般为大型、带状稀疏矩阵，矩阵的非零元素一般集中在对角线区域，为此出现了很多节约存储空间的存储方法，如半带存储、变带宽存储等.这些方法可以减少刚度矩阵的存储空间，但都不可避免地存储了部分非零元素，浪费了储存空间，而且受到节点编号的影响，需要对节点编号进行优化，浪费大量的计算时间.为了进一步节约存储空间，鲍益东等［4］针对板料成形问题提出了一种适合迭代算法的改进一维变带宽压缩存储方法，该方法采用一维数组按行的顺序保存刚度矩阵的非零元素，同时采用2个辅助数组记录列号和每列起始元素在刚度矩阵数组的位置.该方法节约了大量存储空间，也避免了节点编号的优化难题，但该方法采用的辅助数组与刚度矩阵存储数组具有同样长度，仍存在消耗部分存储空间的问题.

本文根据刚度矩阵的组成特点，提出了一种新的刚度矩阵压缩存储方法，该方法在辅助数组中只记录非零子矩阵的位置，间接记录刚度矩阵非零元素的位置，进一步节约了刚度矩阵的存储空间，尤其适合于求解大型、复杂的三维工程问题.

1 刚度矩阵非零元素确定

在有限元网格模型中，同一单元内的任意2个节点构成的节点对(包括节点自身与自身构成的节点对)称为“广义相邻节点对”.根据刚度矩阵的生成原理，有限元刚度矩阵中的非零元素与“广义相邻节点对”有着密切的关系，每组“广义相邻节点对”对应一个与所分析问题维数相同的非零子矩阵，非零子矩阵的位置由广义节点对的全局节点序号决定.例如同一个单元中的2个节点的全局节点编号为(I，J)，构成一个“广义相邻节点对”Bij，该“广义相邻节点对”产生的非零子矩阵在广义矩阵中的位置为I行J列.

如果考虑“广义相邻节点对”的顺序，即Bij和Bji作为2个不同的节点对，它们分别对应第I行、第J列和第J行、第I列的非零子矩阵，有序“广义相邻节点对”与整个刚度矩阵的非零子矩阵数量相同，且一一对应.由于刚度矩阵为对称矩阵，为节约存储空间，可只存储上三角矩阵，因此只需考虑Bij(I≤J)的节点对对应的非零子矩阵，不需考虑节点对的顺序问题.Bij和Bji作为同一个节点对，无序广义节点对与上三角矩阵存储的刚度矩阵的非零子矩阵数量相同，一一对应，因此，完全可以通过无序广义节点对及其数量来确定刚度矩阵中非零子矩阵的数量和位置.

对于如图1所示的八节点六面体单元，其“广义相邻节点对”分为3个类型:一是边相邻节点对，例如节点对12、14、15;二是面相邻节点对，例如节点对16、18、13;三是体相邻节点对，例如节点对17.从整个单元模型来看，边相邻节点对由单元内相邻节点连线的数量决定，每条连线对应1个无序节点对;面相邻节点对的数量由单元面的数量决定，每个面有2条对角线，每条面对角线对应1个无序节点对;体相邻节点对的数量由单元的数量决定，每个单元有4条体对角线，每条体对角线对应1个无序节点对.

图1所示单元模型的无序广义节点对的数量即非零子矩阵的数量，可由式(1)确定:

式中:NS为网格模型无序节点对数量;N1为节点数量，表示节点与自身生成的节点对;N2为同一单元内相邻节点连线的数量，表示边相邻节点对的数量;N3为单元的面数，2N3表示面相邻节点对的数量;N4为单元数量，4N4表示体相邻节点对的数量.

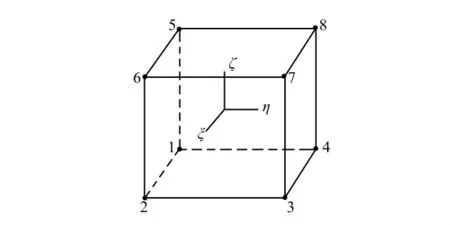
图1 八节点六面体单元模型

对角线非零子矩阵的数量也为N1，每个对角线非零子矩阵只需存储上三角子矩阵和对角线元素，若设N为所求解问题的维数，则所需存储的非零元素为(N2+N)/2.对于三维问题N=3，则每个对角线非零子矩阵只需存储6个数据，其他非零子矩阵需要存储N2=9个数据，因此，总共需要保存的非零刚度矩阵元素数量为

式中，NZ为网格模型非零刚度矩阵元素数量，N1、N2、N3、N4与式(1)中的意义相同.

同理，对于如图2所示的由2个单元构成的简单六面体网格，N1=12、N2=20、N3=11、N4= 2.采用上三角矩阵存储时，其非零子矩阵数量为

总共需要保存的刚度矩阵非零元素数量为

一旦确定了非零子矩阵和非零元素的数量，即可准确地分配刚度矩阵的存储空间，这对于刚度矩阵存储算法的实现具有重要意义.

图2 八节点六面体单元网格模型

2 刚度矩阵的存储方案

稀疏矩阵有多种存储方式，在此采用了比较常用的 CSR格式(Compressed Sparse Row format).该方法采用3个一维数组保存稀疏矩阵，浮点型数组A按行顺序存储矩阵中的各非零元素;整形数组J中记录对应元素所在的列号;整形数组K中记录每行第1个元素在A中的位置.其中A和J的长度相同，即为稀疏矩阵中非零元素的数量，而整形数组K的长度则为稀疏矩阵的维数.例如，对于图3所示的稀疏矩阵，采用CSR格式的存储格式如下所示:

由于刚度矩阵为对称矩阵，可以只存储其上三角矩阵，因此K数组应保存对角线元素在数组A中的位置.CSR方法可以很大程度上减少刚度矩阵的存储空间，而且按行引用，其效率较高，比较适合存储有限元的刚度方程.但是整型数组J与浮点数组A长度一致，占用了大约1/3的存储空间，造成了存储效率的降低.由前面的分析可以看出，有限元刚度矩阵中非零元素的分布是有规律的，只分布于与“广义相邻节点对”对应的非零子矩阵中，因此，只要记录了非零子矩阵的位置，即可间接地确定非零元素的位置，该方法称为改进的CSR方法.对于三维问题，非零子矩阵有9个元素，只记录非零子矩阵的位置，就可以减少数组J的存储空间约90%，进而使整个刚度矩阵的存储空间减少约30%.在此方法中，整形数组J中记录对应非零子矩阵所在的列号;整形数组K中记录广义矩阵中每行第一个非零子矩阵在J中的位置.

下面以如图2所示的单元模型的刚度矩阵为例进行分析，采用CSR方法的J数组数据长度为所有非零元素的数量，即NZ=522，K数组数据长度为刚度方程的维数，即为12×3=36，因此，总数据量为558;而采用改进的CSR方法后，J数组数据长度则为刚度矩阵非零子矩阵数量，即NS= 62，K数组数据长度为单元数量12，则总数据量减少为74.如果只比较2个辅助数组，则改进的CSR方法所节约存储空间为如果浮点型数组A采用单精度浮点数保存，则改进的CSR方法后，整个刚度矩阵所节约的存储空间为

显而易见，改进的CSR方法进一步明显地节约了刚度矩阵的存储空间，但该方法间接表示非零元素的位置，增加了访问刚度矩阵的计算时间消耗，对计算效率有一定的影响，属于以时间换空间的方法.因此建议在单元数量较多时采用改进的CSR方法，以减少内存消耗;而单元数量较少时，则采用前一种方法，提高对刚度矩阵的访问效率，达到最好的综合效益.对于三维体积成形问题，内存不足是分析的主要问题，因此，宜采用能够节约内存的改进的CSR方法.

3 刚度矩阵的生成

在生成刚度矩阵时，首先根据单元模型的拓扑结构来确定非零子矩阵的数量和位置，生成索引数组J、K;然后根据刚度矩阵的生成规则和2个索引数组的数据，将单元刚度矩阵的数据对号入座地进行组合.对于改进的CSR存储方法，还需要对索引数据进行转换.下面通过一个实例说明刚度矩阵的生成过程.

假设一个三维八节点六面体单元，其单元节点的整体编号为I［8］，单元刚度矩阵为U［8× 3］［8×3］，单元刚度矩阵的任意元素可描述为

式中:i、j=1、2、Λ、8为节点局部编号;k、l为物理量维数编号，k、l=1、2、3.其在整体刚度矩阵数组中的序号按如下步骤确定:

1)确定Uijkl的整体节点编号为

式中，I、J为Uijkl所在的非零子矩阵AIJ中的广义行号和列号，非零子矩阵的位置如图3所示.

图3 非零子矩阵分布示意图

2)确定非零子矩阵AII之前非零子矩阵的数量NI:

3)确定非零子矩阵AII之前非零元素的数量NNI:式中，(I-1)×3是由于对角非零子矩阵引起的非零元素的减少项.如图4显示的AII子矩阵只存储了6个非零元素，与其他子矩阵相比少存了3个.

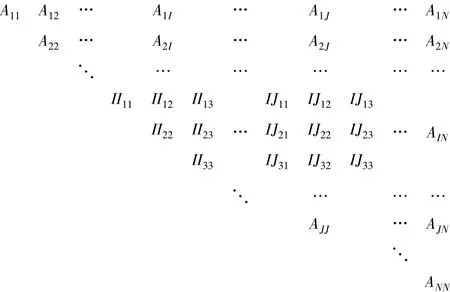
图4 非零元素位置示意图

4)确定第I行非零子矩阵中第k行之前非零元素的数量NNIK(未考虑对角非零矩阵引起的非零元素的减少项):

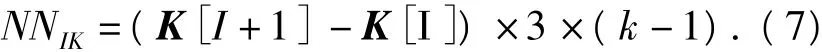
5)搜索数组J从标号K［I］到K［I+1］中J［II］=J的数组标号II，则第I行中，第J列之前的非零子矩阵数量NJ为

确定NJ的列查询是整个刚度矩阵生成过程中消耗时间最多的步骤，而在此步骤当中，普通的CSR方法按元素搜索 ，而改进CSR方法按照子矩阵进行搜索.在三维问题中，普通CSR方法的搜索时间为该进CSR方法搜索时间的3倍，因此，改进的CSR方法在此步骤中较常规CSR方法更节约时间.

6)确定 Uijkl在刚度矩阵中所在行中的编号NNJl:

式中M为由于对角非零子矩阵引起的非零元素的减少项，k=1、2、3时M=0、1、3.

7)确定 Uijkl在刚度矩阵数组 A中的编号NNIJkl:

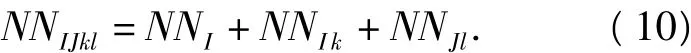
一旦确定了Uijkl在刚度矩阵数组A中的位置后，即可根据刚度矩阵的生成规则进行累加，从而获得总体刚度矩阵.

4 线性方程组的求解

大型有限元方程组的求解方法一般分为直接法和迭代法2种.所谓直接法是指在不考虑舍入误差存在的情况下，经过有限步运算就可以求得方程组的精确解的方法，此方法也称为精确法.而迭代法是一种逐次逼近的方法，它从一个初始向量出发，通过一个给定的计算格式，构造出一个无穷向量列，此向量列即是方程组的近似解，其极限为方程组的精确解.直接法求解精度高、稳定性好，但是在方程数量较多时，求解效率低，因此，在求解大型线性方程组时，往往采用迭代法［5-8］.

线性方程组的迭代方法有很多，其中松弛预处理共额梯度法(SSOR-PCG)是求解对称正定系数矩阵最受欢迎的方法之一.SSOR-PCG方法的基本原理如下［9］.

设线性方程组(11)的系数矩阵A为n阶对称正定矩阵，

设M=(STS)-1为对称正定矩阵，则上式等价于

式中A'=SA ST，b'=Sb，u'=S-Tu.

M通常取为对称逐步超松弛迭代法(SSOR法)的分裂矩阵，即

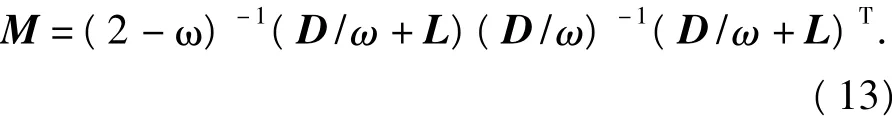
式中:0＜ω＜2，为松弛因子;D为A的对角阵;L为A的严格下三角阵，即

在改进的SSOR-PCG方法中，不必对M求逆，也不必另开辟数组存放M矩阵，计算中仅对A的非零元素进行运算，所以仅需存储A的下三角阵(或上三角阵)中的非零元素，因此，该方法特别适合于本文中只存储非零子矩阵的刚度方程.

5 算例分析与讨论

为了验证本文所提出的算法在节约内存、提高计算效率方面的效果，将刚度矩阵压缩存储方法应用于自行开发的三维体积成形有限元分析程序CasForm中［10］.以如图5所示的道钉成形为例，从内存占用和计算效率两个方面，将本文提出的压缩存储、迭代求解的算法与半带存储、直接求解的算法进行了比较.

图5 道钉成形模拟结果示意图

在内存占用方面，以八节点六面体单元模型为例，按照刚度方程采用单精度浮点数保存，即每个数据占用4个字节;辅助数组采用整形数据保存，即每个数据占用2个字节.在不同的节点和单元数量下，对采用不同方式存储的刚度矩阵所占存储空间进行比较，结果见表1.

表1 不同存储方法存储空间的比较

从表1可以看出，压缩存储方法所占的存储空间远远小于半带存储方法的存储空间，存储空间节约超过90%，而且随着节点数量的增加，空间节约的比例逐渐增大.这主要是因为压缩存储方法只保存了刚度矩阵的非零元素，刚度矩阵中每一行非零元素的数量仅与该行对应节点的广义相邻节点的数量有关，而与整体模型节点的数量无关.换言之，对于压缩存储方法，存储空间与节点数量的正比关系仅与刚度矩阵的行数增加有关，呈线性变化趋势.而对于半带存储方法，每一行的存储空间由刚度矩阵的半带宽决定，随节点数量增加，半带宽一般也随之增加，因此，随节点数量增加，不仅刚度矩阵的行数增加，而且每行需要存储的数据也有所增加，因而呈现抛物线变化趋势.由此可知，随着节点数量的增加，半带存储方法所需的存储空间呈二次幂指数函数增加，而采用压缩存储方法，其节约空间的比例更加显著.

在计算效率方面，以求解单个方程的计算效率为例，对半带存储直接求解和压缩存储迭代求解两种方法的进行了比较，结果见表2.从表2可以看出，压缩存储迭代求解的效率远远高于半带存储直接求解的效率，而且节点数量越多，效率提高越明显.

表2 不同单元模型不同存储方法求解效率的比较

6 结论

1)依据由网格拓扑结构决定的“广义相邻节点对”，可以确定有限元刚度矩阵中非零子矩阵的分布和数量.

2)采用改进的CSR存储方法保存有限元刚度矩阵，可显著减少刚度矩阵的存储空间，而且节点数量越多，空间节约的比例越大.

3)采用基于压缩矩阵的SSOR-PCG迭代方法求解有限元线性方程组，可显著提高方程组的求解效率，而且节点数量越多，求解效率提高的幅度越大.

［1］ GHAEI A，MOVAHHEDY R M.Die design for the radial forging process using 3D FEM［J］.Journal of Materials Processing Technology，2007，182:534-539.

［2］ BEHRENS B A.Finite element analysis of die wear in hot forging processes［J］.CIRP Annals-Manufacturing Technology，2008，57:305-308.

［3］ LU C，ZHANG L W，MU Z J，et al.3D FEM simulation of the multi-stage forging process of a gas turbine compressor blade［J］.Journal of Materials Processing Technology，2008，198:463-470.

［4］ 鲍益东，杜国康，陈文亮，等.冲压成形模拟中有限元方程组求解算法［J］.南京航空航天大学学报，2009，41(5):606-610. BAO Yi-dong，DU Guo-kang，CHEN Wen-liang，et al. Solving algorithm for finite element equations in sheet metal forming simulation［J］.Journal of Nanjing University of Aero nautics＆Astronautics，2009，41(5): 606-610.

［5］ 张永杰.大型稀疏方程组预处理迭代快速求解技术研究［D］.西安:西北工业大学，2006.

［6］ 刘艳芳，施法中，徐向阳.板料冲压成形数值模拟中有限元方程求解算法的研究［J］.塑性工程学报，2006，13(4):15-19. LIU Yan-fang，SHI Fa-zhong，XU Xiang-yang.Study on algorithms of solving FE equations in the numerical simulation of sheet metal stamping［J］.Journalof Plasticity Engineering，2006，13(4):15-19.

［7］ 李静，陈健，云周晶.改进的SSOR-PCG迭代法在接触问题研究中应用［J］.大连理工大学学报，2006，46(4):533-537. LI Jing，CHEN Jian，YUN Zhou-jing.Application of an improved SSOR-PCG iteration method to contact problems［J］.Journal of Dalian University of Technology， 2006，46(4):533-537.

［8］ 包劲青，杨强，陈英儒，等.对称超松弛预处理共轭梯度法在高拱坝整体大规模弹塑性有限元分析中的应用［J］.水利学报，2009，40(5):589-594. BAO Jin-qing，YANG Qiang，CHEN Ying-ru，et al.Application of symmetric successive over relaxation precondition conjugate method to large-scale elasto-plastic FEM analysis for high arch dams［J］.Journal of Hydraulic Engineering，2009，40(5):589-594.

［9］ 林绍忠.对称逐步超松弛预处理共轭梯度法的改进迭代格式［J］.数值计算与计算机应用，1997(4): 266-270. LIN Shao-zhong.Improved iterative format of symmetric successive over relaxation-preconditioned conjugated gradient method［J］.Numerical Methods and Computer Applications，1997(4):266-270.

［10］ 王忠雷，赵国群，黄丽丽，等.六面体网格体积成形有限元分析关键技术［J］.材料科学与工艺，2010，18(4):509-513. WANG Zhong-lei，ZHAO Guo-qun，HUANG Li-li，et al.Key technologies of 3D FEM analysis system for bulk forming with hexahedral mesh［J］.Materials Science＆Technology，2010，18(4):509-513.

Compressed storage algorithm of 3D-FEM stiffness matrix

WANG Zhong-lei1，2，ZHAO Guo-qun1，MA Xin-wu1
(1.Key Laboratory for Liquid-Solid Structural Evolution and Processing of Materials(Ministry of Education)，Shandong University，Jinan 250061，China;2.Institute of Electrical and Mechanical，Shandong Architectural University，Jinan 250101，China)

To improve the efficiency and reduce the storage space of finite element analysis，compression and storage algorithm of 3D-FEM stiffness matrix is studied.The relationship between“generalized adjacent double nodes"and the non-zero sub-matrix in stiffness matrix is researched for getting distribution of non-zero sub-matrix in stiffness matrix.A new algorithm of stiffness matrix of compressed storage-”improved CSR storage method"is proposed.Based on the algorithm，the generation process of stiffness matrix is given and iterative solution of linear equations method is proposed to improve the efficiency of solving linear equations.The algorithm is applied to the three-dimensional bulk forming finite element analysis software and the numerical results show that the algorithm can effectively decrease the storage space and improve the computation efficiency.

3D-FEM;stiffness matrix;compressed storage;hexahedral mesh

TG316.8 文献标志码：A 文章编号：1005-0299(2012)02-0096-05

2011-02-21.

国家自然科学基金资助课题(50875155);教育部“长江学者和创新团队发展计划”创新团队资助项目(IRT0931).

王忠雷(1977-)，男，博士研究生;

赵国群(1962-)，男，教授，博士生导师.

赵国群，E-mail:zhaogq@sdu.edu.cn.

(编辑 程利冬)