纤锌矿GaN/AlxGa1－xN量子阱材料中极化子效应

乌仁图雅，段旭来，赵凤岐，苏日古嘎

(内蒙古师范大学物理与电子信息学院，内蒙古功能材料物理与化学重点实验室，呼和浩特010022)

纤锌矿GaN/AlxGa1－xN量子阱材料中极化子效应

乌仁图雅，段旭来，赵凤岐，苏日古嘎

(内蒙古师范大学物理与电子信息学院，内蒙古功能材料物理与化学重点实验室，呼和浩特010022)

采用Lee-Low-Pines(LLP)变分法研究纤锌矿量子阱材料中电子-声子相互作用有关问题，给出纤锌矿GaN/AlxGa1-xN和InxGa1-xN/GaN量子阱材料中极化子基态能量和第一激发态到基态的跃迁能量随量子阱宽度和材料组分的变化关系.研究中考虑了纤锌矿量子阱材料中光学声子模各向异性以及声子频率随波矢的变化关系.同时还对运用LLP变分方法计算极化子能量时所采用的几种不同处理方法进行了分析和讨论，并给出相应的数值计算结果.

纤锌矿;量子阱;极化子

GaN基半导体是一类重要的宽禁带半导体，它具有高击穿电场、高电子饱和漂移速度和强的抗辐射能力等优点.用它非常适合研制高温、高功率微波器件和在恶劣环境下工作的各类电子器件.纤锌矿氮化物量子阱材料已应用到蓝光发射二极管［1-2］、激光二极管［3-4］，紫外线光电探测器［5］等器件中.由于GaN基半导体材料具有与以往的第一、二代半导体所没有的特殊物理现象，因而近年来，GaN基半导体材料中电子态问题不断引起许多科研工作的关注［6-12］.

B.C.Lee［6］等采用介电连续和伦敦单晶模型，研究了纤锌矿单、双异质结材料中的电子-光学声子相互作用，导出该结构中电子与各支光学声子相互作用哈密顿量.他们指出纤锌矿量子阱材料中除了具有闪锌矿中所具有的定域模，半空间模和界面模外，还存在传播模.史俊杰［7-9］等人通过转移矩阵法研究纤锌矿异质结材料中的光学声子色散关系，导出电子与各支光学声子相互作用哈密顿量.纤锌矿量子阱材料中纵光学声子和横光学声子是分不开，以混合模的形式存在［10，11］.

史俊杰等［13-15］用他们导出的电子-声子相互作用哈密顿量出发研究纤锌矿GaN/AlxGa1-xN量子阱材料中电子-声子相互作用有关的问题，并给出了相应的数值计算结果.赵凤岐［16-18］等利用B.C.Lee［6］导出的电子-声子相互作用哈密顿量，对纤锌矿GaN/AlxGa1-xN抛物量子阱材料中电子-声子相互作用进行了研究，给出了极化子基态能量、第一激发态能量和跃迁能量随阱宽及外场的变化关系.屈媛等［19］结合介电连续和单轴晶体模型导出含纤锌矿三元混晶InxGa1-xN和AlxGa1-xN单量子阱材料中各类光学声子模的色散关系，进一步分析了声子模随组分X的变化关系.最近，文献［20］中利用B.C.Lee［6］导出的电子-声子相互作用哈密顿量讨论了纤锌矿GaN/ AlxGa1-xN量子阱材料中束缚极化子结合能等问题.但是，对纤锌矿量子阱材料中电子与声子相互作用对电子行为影响的认识仍比较粗浅，有待于进一步深入研究.

本文在考虑晶格振动频率单轴异性情况，利用LLP变分法，研究了纤锌矿GaN/AlxGa1-xN和InxGa1-xN/GaN量子阱材料中电子-定域声子作用，给出极化子能量和跃迁能量随量子阱宽度L及组分X的变化关系.同时介绍了LLP变分法中采用的三种处理方法，并对三种处理方法进行了分析和讨论.

1 理论计算

考虑纤锌矿 GaN/AlxGa1-xN(InxGa1-xN/ GaN)材料构成的量子阱结构，阱宽为2d，且沿z轴方向生长，即z轴垂直于界面，x-y平面平行于界面.阱内材料位于区间|z|＜d，(λ=1)，垒材料位于区间|z|≥d，(λ=2).采用有效质量近似，该系统(极化子)的哈密顿可写为

式中:p⇀=(p⇀xy，p⇀z)是电子的动量，mλ是电子的有效带质量，a+wj(awj)是波矢为w⇀=(q⇀，kz)、频率为ω的对称(j=S)和反对称(j=A)声子产生算符(湮灭算符).方程(1)中第二项是势能，可表示为

在GaN/AlxGa1-xN量子阱中

对纤锌矿结构，Qi=0.7，b=1.0eV［21］，对闪锌矿结构，Qi=0.6，b=0.53 eV［21］.

在纤锌矿(闪锌矿)InxGa1-xN/GaN量子阱中

其中，Qi=0.7，b=1.4eV［22］.EgGaN和EgAlN和EgInN分别表示相应材料的带隙.

其中方程(1)中最后一项是电子—声子相互作用哈密顿量［6］

对于纤锌矿量子阱中的对称定域模

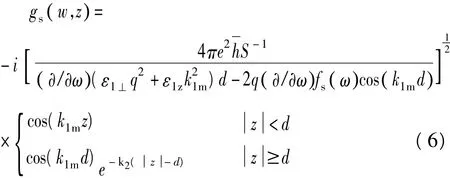
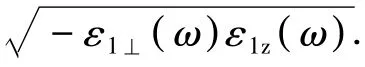
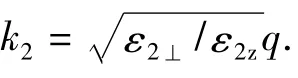
从纤锌量子阱矿材料中电子—声子相互作用哈密顿量看，它比闪锌矿中的电子—声子相互作用哈密顿量复杂的多.因此在纤锌矿量子阱材料中处理电子—声子相互作用问题比闪锌矿量子阱材料中相应问题难.

为了简化系统的哈密顿量，需要进行两次幺正变换，以消去哈密顿量中的电子坐标和将晶格振动从原点移到平衡点上.两次幺正变换的形式为

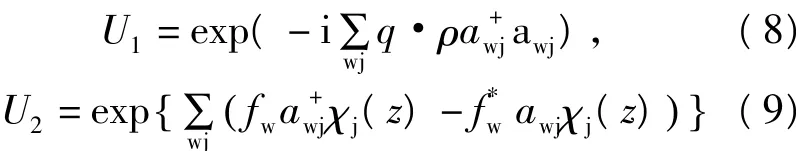
上式中，fw(f*w)是变分参数.对于对称模，χj(z)为

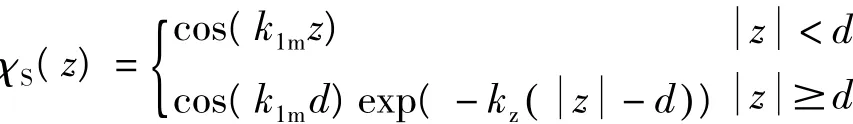
(10)

对于反对称模，χj(z)为

幺正变换后得到系统的哈密顿量为

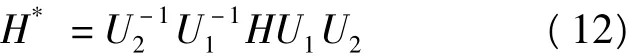
选取系统的波函数

则极化子能量为

由能量对fw(f*w)求极值条件

可以确定fw(f*2)

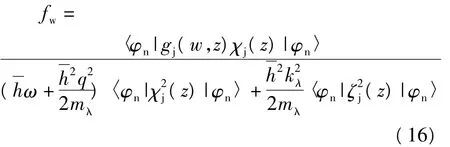
将上述变分参数带入能量的表达式，得到

其中，E0n是电子在量子阱中的子带能量，ζj(z)是χj(z)的导数.

对基态，波函数φ1(z)选为

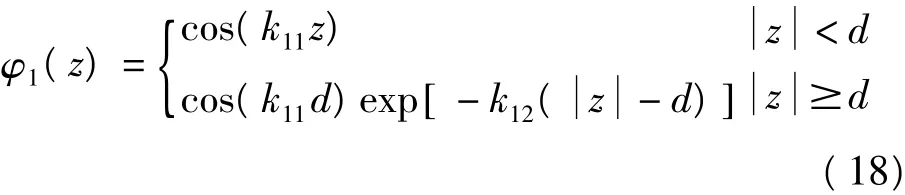
对激发态，波函数φ2(z)选为

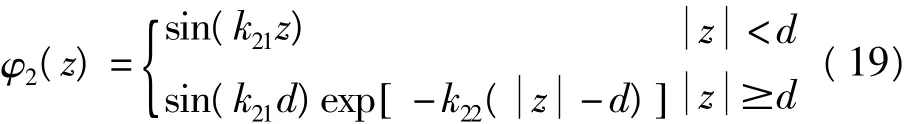
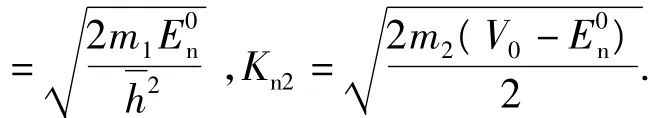
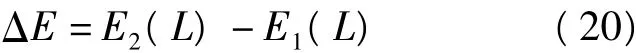
在运用LLP变分法处理极化子能量时，主要有三种方法.这三种方法的差别是在幺正变换U2中变分参数fw的选择不同.

方法一是在文献［23］和本文中所使用的方法.该方法中变分参数的选择和能量表达式为方程(16)和(17)中给出.

方法二是在文献［17-18，24-25］中采用的方法.该方法中

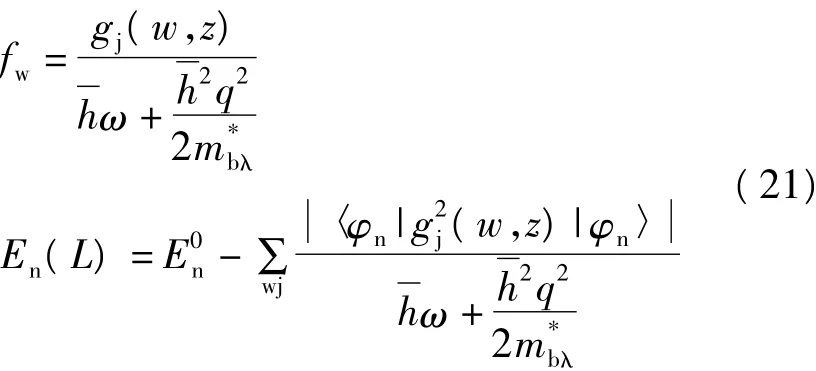
方法三是在文献［26-27］中采用的方法，该方法中

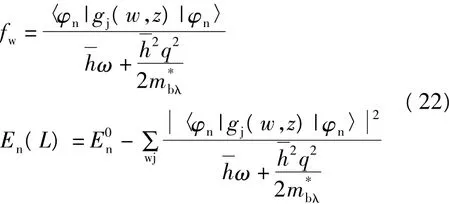
以上三种方法中fw的取值不同，因此得出的结果有所不同.

2 结果与讨论

利用方程(16)～(22)，对纤锌矿(闪锌矿) GaN/AlN、GaN/AlxGa1-xN、纤锌矿 InxGa1-xN/ GaN量子阱材料中的极化子能量进行了数值计算.数值计算中用到的相关参数在表1和表2中给出，数值计算的结果在图1-4中给出［28-35］.

三元混晶AlxGa1-xN和InxGa1-xN)材料的参数根据线性内插法求得［36］，即QAlxGa1-xN=(1-x) QGaN+xQAlN和QInxGa1-xN=(1-x)QGaN+xQInN.

表1 纤锌矿结构中GaN、AlN的相应参数

表2 闪锌矿结构中GaN和AlN的相应参数

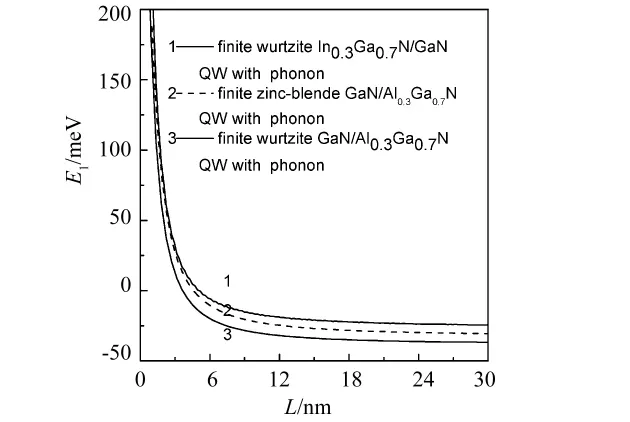
图1 量子阱中极化子基态能量E1随阱宽L的变化关系

图1中给出了纤锌矿 GaN/Al0.3Ga0.7N和In0.3Ga0.7N/GaN量子阱材料中极化子基态能量随阱宽L的变化关系.从图看出，极化子基态能量随阱宽的增大而减小，窄阱时，能量下降的速度快，阱宽增大时，下降的速度较慢，最后趋近于体材料GaN和In0.3Ga0.7N的三维值.这一变化规律与电子在量子阱中受到的量子限制有关.因为在窄阱时，电子受到的量子局域效应较强，使极化子基态能量较大;随着阱宽增加，电子所受的量子局域效应减弱，这就导致极化子基态能量降低.为了进行对比分析，图中还给出了闪锌矿GaN/Al0.3Ga0.7N量子阱材料材料中极化子基态能量随阱宽的变化关系.纤锌矿结构中极化子基态能量大于闪锌矿结构中的相应值，这些差别主要是由于纤锌矿结构材料的单轴异性，即电子有效带质量、介电常数、声子频率、能带宽度等参数不同于闪锌矿结构材料中的相应参数导致的.

图2给出了给定阱宽条件下极化子基态能量随着组分X变化的函数关系.从图2看出，基态能量随着量子阱材料组分x的增加而增大，并且在阱宽较窄时(4nm)这种增加较为明显，而当阱宽较宽时(15nm)，变化逐渐趋于平缓.这是因为阱宽相同时，随着组分X的增加，量子阱深度变大，这就增强了量子限制效应，从而导致基态能量随着量子阱材料组分x的增加而增加.从图2中还看出，电子-声子相互作用对极化子能量的贡献比较大，使基态能量明显降低.比如阱宽为15nm时，纤锌矿GaN/Al0.3Ga0.7N量子阱中的值约为35meV，闪锌矿GaN/Al0.3Ga0.7N量子阱中的值约为31meV，纤锌矿In0.3Ga0.7N/GaN量子阱中的值约为26meV.这些值的不同是由于结构材料的单轴异性以及相关参数不同有关.从上述分析看，GaN/Al0.3Ga0.7N和In0.3Ga0.7N/GaN量子阱材料中电子-声子相互作用对极化子能量的贡献远大于GaAs/Al0.3Ga0.7As量子阱结构中的相应值(2.4meV).因此，在研究氮化物量子阱材料中极化子问题时，应该考虑电子-声子相互作用的影响.

图2 给定阱宽条件下，GaN/AlxGa1－xN量子阱和

图3 GaN/Al0.3Ga0.7N量子阱中极化子跃迁能量随阱宽L(a)和组分X(b)的变化关系

图3(a)和(b)分别给出了纤锌矿(闪锌矿) GaN/Al0.3Ga0.7N量子阱材料中极化子第一激发态到基态跃迁能量随阱宽和组分的变化关系.从图3(a)中可知，跃迁能量随阱宽的增大而减小，阱宽较小时减小的速度快，随着阱宽的增大，减小的速度变慢，最后缓慢趋近于体材料的三维值.从图3(a)中还可以发现，纤锌矿结构中的跃迁能量小于闪锌矿结构中的相应值.这是由于纤锌矿结构中介电常数、有效质量和声子频率等参数不同于闪锌矿结构中的相应参数导致的.从图3(b)看出，当量子阱宽度较窄时(4nm)，跃迁能量随Al组分X的增加而显著增加，而当量子阱宽度较宽时(15nm)，跃迁能量随组分X的增加而变化非常小.这规律与电子在量子阱结构中受量子限制有关.

半导体量子阱材料中处理电子-声子相互作用问题时，经常采用LLP变分方法.由于在变换过程中第二次幺正变换的变分参数采取了不同的形式，得到的结果就有所差别.这里我们对常用的三种方法进行对比分析.图4中给出了不同方法得出的闪锌矿量子阱中电子-定域声子相互作用对极化子基态能量的贡献随量子阱宽度的变化关系.从图4中可以看出，方法二(曲线1)得到的电子-定域声子相互作用对极化子基态能量的贡献比较大，除了窄阱情况外均大于体材料中的相应值.方法三(曲线4)得到结果比较小，并且从某一阱宽开始随着阱宽的增大而减小.方法一(曲线3)得到的结果随着阱宽的增大而增大，在阱宽较大时，接近体材料中的相应值.在理论上说电子与定域声子相互作用由于阱宽的增大，电子穿过量子阱势垒的几率变小，电子被局域在阱内，使得电子与定域声子相互作用增强，在量子阱比较宽时，电子与定域声子相互作用能量应该接近电子-体声子相互作用能量.因此用方法一得到的结果最符合于实际情况，而方法二和方法三得到的结果与实际情况有明显的差距.在过去，讨论GaAs/ AlxGa1-xAs量子阱中极化子问题时，由于电子-声子相互作用对能量的贡献比较小(约2.4 meV)，三种方法得出结果的差异没那么被重视.目前，讨论GaN/AlxGa1-xN量子阱中极化子问题时由于电子-声子相互作用对能量的贡献较大(约38 meV)，因此，应该考虑三种方法的合理性.

图4 闪锌矿量子阱中电子－定域声子相互作用对极化子基态能量的贡献随量子阱宽度的变化关系

3 结论

本文考虑了纤锌矿GaN、AlN、InN材料的单轴异性及声子频率随波矢的变化关系，采用LLP变分法研究了纤锌矿(闪锌矿)GaN/AlxGa1-xN和InxGa1-xN/GaN量子阱材料中极化子基态能量和第一激发态到基态的跃迁能量随量子阱宽度及组份的变化关系.数值计算结果得出，纤锌矿(闪锌矿)GaN/Al0.3Ga0.7N和 In0.3Ga0.7N/GaN材料中极化子基态能量，第一激发态到基态的跃迁能量随量子阱宽度增大而减小，最后趋近于相应体材料的值.而基态能量和跃迁能量随量子阱材料组分的变化而缓慢变化.纤锌矿GaN/Al0.3Ga0.7N量子阱材料中电子-定域声子相互作用对极化子能量的贡献(约35meV)大于闪锌矿 GaN/Al0.3Ga0.7N量子阱材料中的相应值(约31meV)和纤锌矿 In0.3Ga0.7N/GaN量子阱中的相应值(约26meV).GaN/Al0.3Ga0.7N和 In0.3Ga0.7N/GaN量子阱中电子-定域声子相互作用对能量的贡献比GaAs/Al0.3Ga0.7As量子阱中的相应值(2.4meV)大得多.因此，在讨论GaN/Al0.3Ga0.7N和InxGa1 -xN/GaN量子阱材料中电子态问题时应该考虑电子-声子相互作用.研究还发现，用LLP变分方法处理半导体量子阱中电子-声子相互作用问题时所采用的三种方法中，方法一得到的结果较好，它符合于实际情况，而方法二和方法三得到的结果与实际情况有明显的差距.因此，讨论量子阱中电子-声子相互作用时采用第一种方法比较合理.

［1］ MALYUTENKO V K，BOLGOV S S，PODOLTSRV A D.Current crowding effect on the ideality factor and efficiency droop in blue lateral InGaN/GaN light emitting diodes［J］.Appl.Phys.Lett.，2010，97(25): 251110-251112.

［2］ LEE W，KIM M H，ZHU D，et al.Growth and characteristics of GaInN/GaInN multiple quantum well lightemitting diodes［J］.J.Appl.Phys.2010，107(6) 063102-063107.

［3］ ZHAO H，TANSU N.Optical gain characteristics of staggered InGaN quantum wells lasers［J］.J.Appl. Phys.2010，107(11):113110-113121.

［4］ YOSHIDA H，KUWABARA M，YAMASHITA Y，et al. Radiative and nonradiative recombination in an ultraviolet GaN/AlGaN multiple-quantum-well laser diode［J］.Appl.Phys.Lett.，2010，96(21):211122-211124.

［5］ RAZEGHI M，ROGALSKI A.Semiconductor ultraviolet detectors.J.Appl.Phys.，1997，79(10):7433-7473.

［6］ LEE B C，KIM K W，STROSCIO M A，et al.Opticalphonon confinement and scattering in wurtzite heterostructures［J］.Phys.Rev.B，1998，58(8):4860-4865.

［7］ SHI J J.Interface optical-phonon modes and electroninterface-phonon Interactions in wurtzite GaN/AlN quantum wells［J］.Phys.Rev.B，2003，68(16): 165335-1-165335-11.

［8］ LI L，LIU D，SHI J J.Electron quasi-confined-opticalphonon interaction in wurtzite GaN/AlN quantum well［J］.Eur.Phys.J.B，2005，44(4):401-413.

［9］ ZHU Y H，SHI J J.Effects of built-in-electric field on polarons in wurtzite GaN/AlN quantum well［J］. Physica E，2009，41 746-752.

［10］ KOMIRENKO S M，KIM K W，STROSCIO M A.，et al.Dispersion of polar optical phonons in wurtzite quantum wells［J］.Phys.Rev.B，1999，59(7): 5013.-5020.

［11］ GLEIZE J，RENUCCI M A，FRANDON J，et al.Anisotropy effects on polar optical phonons in wurtzite GaN/AlN superlattices［J］.Phys.Rev.B，1999，60 (23):15985-15992.

［12］ 赵凤岐，萨初荣贵，乌仁图雅.纤锌矿 GaN/Al0.3Ga0.7N量子阱中磁极化子能量［J］.光学学报，2011，31(4):0416003-1-0416003-7.

［13］ LIU D，SHI J J，BUTCHER K S A.Impurity bound polaron in wurtzite GaN/AlN quantum wells:The interface optical-phonon and the built-in electric field effects［J］.Superlattices and Microstructures，2006，40(3):180-190.

［14］ ZHANG L，SHI J J.Vibration spectra of quasi-confined optical phonon modes in an asymmetric wurtzite AlxGa1-xGaN/GaN/AlyGa1-yN quantum well［J］. Commun.Theor.Phys.，2007，47(2):349-354.

［15］ CUI J，SHI J J.Exciton state in wurtzite InGaN/AlN quantum wells:strong built-in-electric field and interface-optical-phonon effects［J］.Solid State Commun，2008，145(5):235-240.

［16］ 赵凤岐，周炳卿.外电场作用下纤锌矿氮化物抛物量子阱中极化子能级［J］.物理学报，2007，56(8): 4856-4862.

［17］ ZHAO F Q，GOGN J.Energy of a Polaron in a wurtzite nitride finite parabolic quantum well［J］.Chin. Phys.Lett.，2007，24(5):1327-1330.

［18］ 赵凤岐，色林花，萨茹拉，乌仁图雅.氮化物抛物量子阱中电子-声子互作用对极化子能量的影响［J］.内蒙古师范大学学报，2006，35(4):419-423.

［19］ 屈媛，班士良.纤锌矿AlN/GaN/InN/GaN/AlN量子阱的界面和局域光学声子［J］.内蒙古大学学报，2010，41(1):57-65.

［20］ ZHAO F Q，ZHANG M.Bound polarons in wurtzite GaN/AlxGa1-xN quantum-well［J］.Phys.Stat.Sol. C，2011，8:62-65.

［21］ WANG H，FARIAS G A，FREIRE V N，Interface-related exciton energy blueshift in GaN/AlxGa1-xN zinc-blende and wurtzite single quantum well［J］. Phys.Rev B，1999，60(8):5705-5713.

［22］ VURGAFTMAN I，MELYER J R.Band parameters for nitrogen-containing semiconductors.J.Appl.Phys.，2003，94(6)3675-3696.

［23］ ZHENG R S，BAN S L，LIANG X X.Effects of interface and bulk optical phonons on polarons in a quantum well［J］.Phys.Rev.B，1994，49(3):1796-1801.

［24］ 赵国军，梁希侠，班士良.极性半导体窄量子阱中的激子结合能［J］.内蒙古大学学报，1999，30(4): 486-493.

［25］ 赵国忠，梁希侠，王 旭.对称量子阱中电子-界面声子相互作用对极化子性质的影响［J］.内蒙古大学学报，1995，26(3):270-279.

［26］ 元丽华，王 旭，姜金龙.抛物阱中束缚极化子的结合能［J］.兰州理工大学学报，2006，32(4):162 -164.

［27］ 梁希侠，王 旭，GaAs-GaAlAs量子阱中定域光学极化子［J］.内蒙古大学学报，1992，23(1):81-87.

［28］ VURGAFTMAN I，MEYER J R，RAM-MOHAN L R. Band parameters for III-V compound semiconductors and their alloys［J］.J.Appl.Phys.，2001，89(11): 5815-5875.

［29］ AZUHATA T，SOTA T，SUZUKI K，et al.Polarized raman spectra in GaN［J］.J.Phys.Condens.Matter，1995，7(10):L129-L133.

［30］ PERLIN P，POLIAN A，SUSKI T.Raman-scattering studied of aluminum nitride at high pressure［J］. Phys.Rev.B，1993，47(5):2874-2877.

［31］ BEMARDMI F，FIORENTINI V.Electronic dielectric constants of insulators calculated by the polarization method［J］.Phys.Rev.B，1998，58(23):15292-15295.

［32］ HARIMA H.Roperties of GaN and related compounds studied by means of Raman scattering［J］.J.Phys.: Condens.Matter，2002，14(38):R967-R973.

［33］ KARCH K，BECHSTEDT F，PLETL T.Lattice dynamiics of GaN:effect of 3d electron［J］.Phys.Rev. B，1997，56(7):3560-3563.

［34］ KIM K，LAMBRECHT W R，SEGALL B.Elastic constants and related properties of tetrahedrally bonded BN，AlN，GaN，and InN［J］.Phys.Rev.B，1996，53 (24):16310-16326.

［35］ KARCH K，BECHSTEDT F.Ab initio lattice dynamiics of BN and AlN a Acovolent versus ionic forces［J］.Phys.Rev.B，1997，56(12):7404-7415.

［36］ LIANG X X，YANG J S.Effective-phonon approximation of polarons in ternary mixed crystals［J］.Solid State Commun.，1996，100(9):629-634.

The effect of polaron in wurtzite GaN/AlxGa1-xN quantum well

Wurentuya，DUAN Xu-lai，ZHAO Feng-qi，Suriguga
(College of Physics and Electronic Information，Inner Mongolia Normal University，Inner Mongolia Key Laboratory for Physics and Chemistry of Functional Materials，Huhhot 010022，China)

The problem related to the interaction between the electron and phonons in wurtzite quantum well structures are studied by using modified Lee-Low-Pines(LLP)variational method.The ground state energy and the first excited state to ground state transition energy of polaron in wurtzite(zinc-blende)GaN/AlxGa1-xN and InxGa1-xN/GaN wurtzite quantum well as functions of the well width and composition are given.The anisotropy of optical phonon modes and the relation of the phonon frequency changing with vector are considered in the investigation.Meanwhile，The several different methods of culcalating the polaron energy problems by using LLP methods in transformation process are analyzed and discussed，and the corresponding nummerical results are given.

wurtzite;quantum well;polaron

O471.3，O471.1 文献标志码：A 文章编号：1005-0299(2012)02-0133-07

2011-04-05.

国家自然基金(10964007)资助项目;内蒙古自然基金资助项目(2009MS0110);内蒙古自治区高等学校科学研究项目(NJ09026).

乌仁图雅(1977-)，女，讲师.

(编辑 张积宾)