(2+1)维Burgers系统的周期孤立波解

傅海明 ,戴正德

(1.广州华夏职业学院基础部,广东广州510935;2.云南大学数学与统计学院,云南昆明650091)

非线性波方程被广泛地应用于物理、工程技术和数学等众多学科分支中,如非线性光学、量子论、流体力学、弹性理论和凝聚态物理等。随着非线性科学的蓬勃发展,传统的求解非线性波方程的方法主要有逆散射法[1]、Backlund法[2]、Darboux变换法[3]、Hirota双线性法[4]、Painlevé展开法[5]等。近年来,结合计算机代数和符号计算,人们发展了许多求解非线性波方程的新方法,如双曲函数法[6]、齐次平衡法[7]、Jacobi椭圆函数展开法[8]、包络变换法[9]、ADM方法[10]和利用分支理论直接积分的方法[11]等。最近,范恩贵[12]提出了一种基于符号计算的代数方法,与绝大多数方法相比,该方法可用于构造各种行波解,包括孤波解、双曲函数解、三角函数周期解、有理函数解、Jacobi和Weierstrass椭圆函数周期解。

本文利用扩展了的Hirota法得到Burgers方程

的新的周期孤波解和一个新形式的解。

1 Burgers方程的精确解

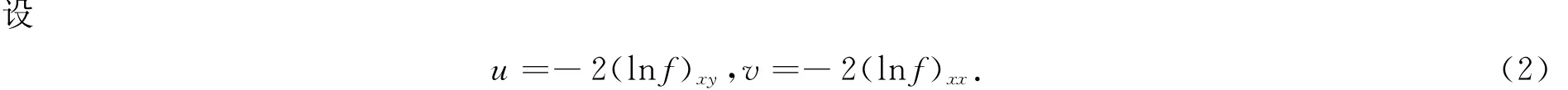
引进双线性算子

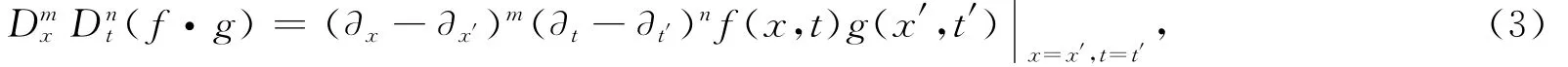
方程(1)通过式(2)和式(3)可以写成双线性型形式

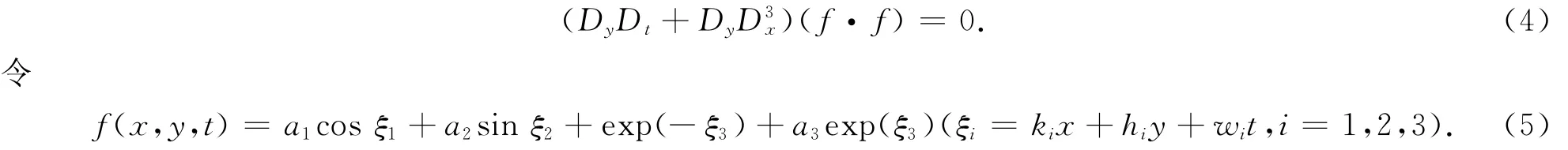
把式(5)代入式(4),得到如下代数方程组

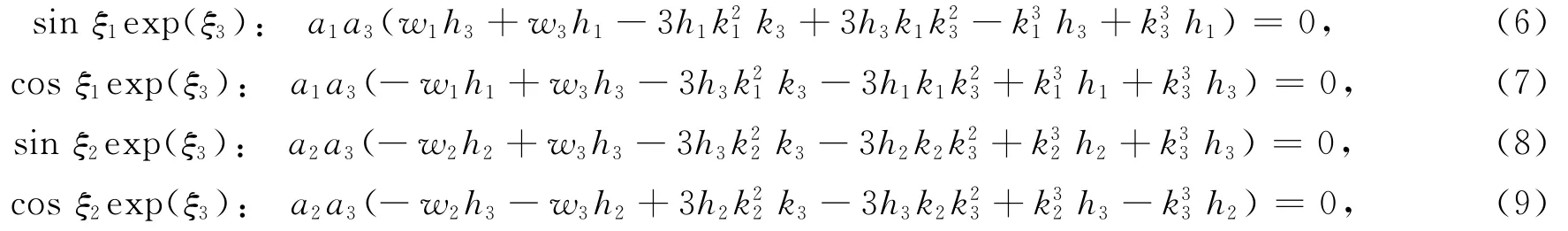
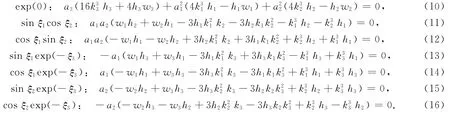
解以上方程组,得:

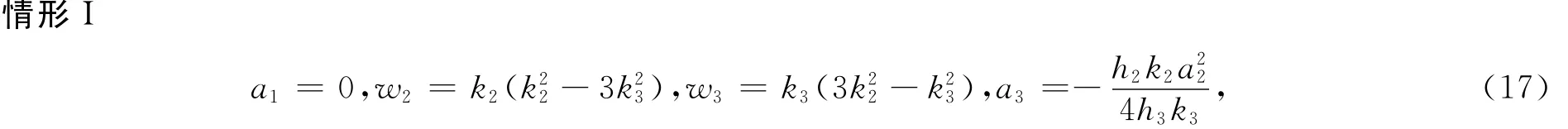
其中h2,h3,k2,k3,a2为任意常数。把式(1 7)代入式(5)得

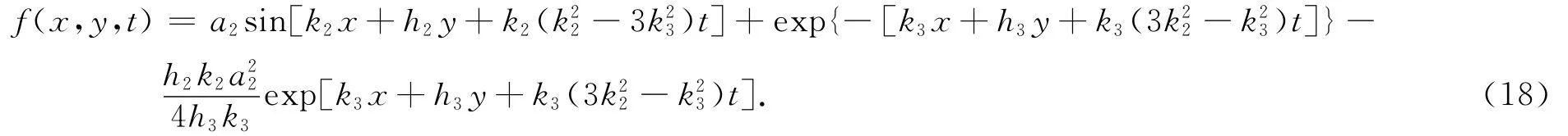
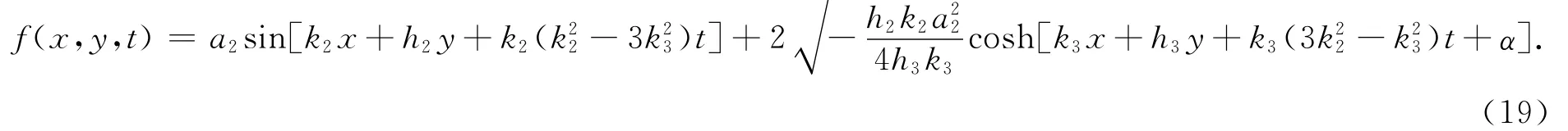
把式(1 9)代入式(2)得方程(1)的解为

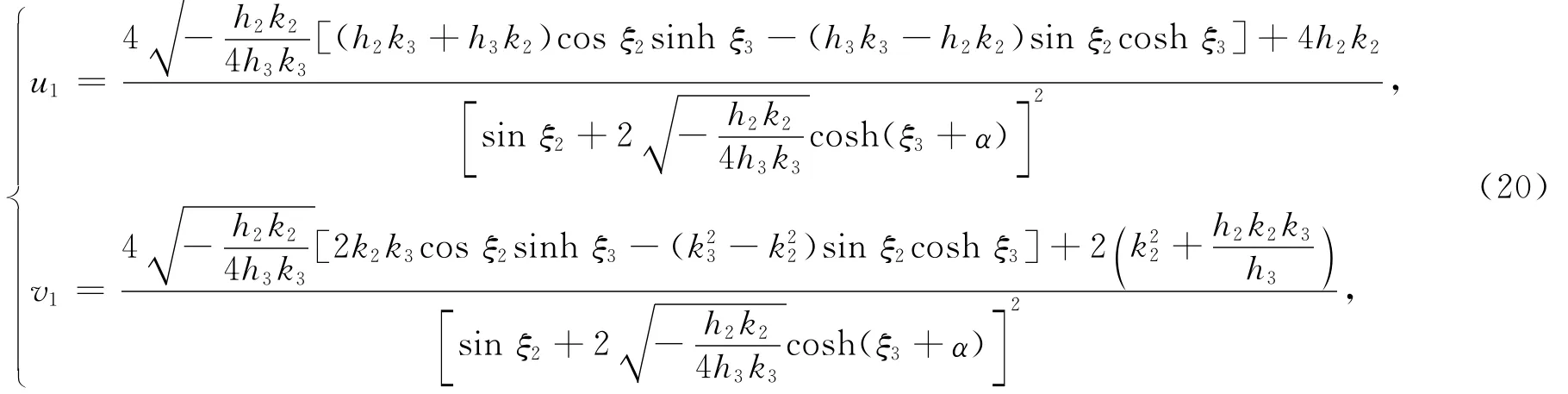
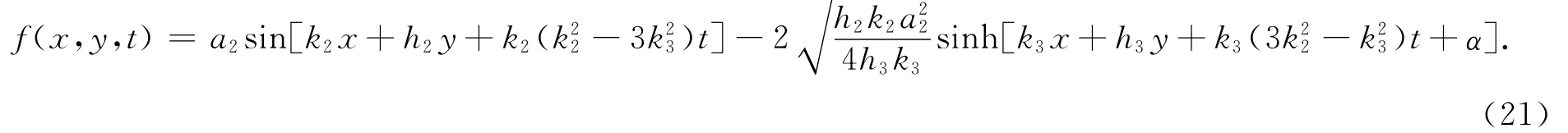
把式(2 1)代入式(2)得方程(1)的解为

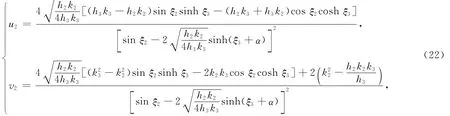
其中ξ2=k2x+h2y+k2(k-3k)t,ξ3=k3x+h3y+k3(3k-k)t。

情形I I

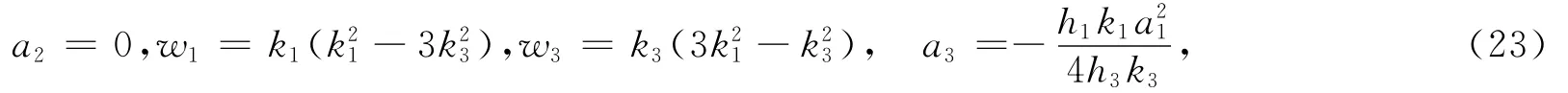
其中h1,h3,k1,k3,a1为任意常数。把式(2 3)代入式(5)得

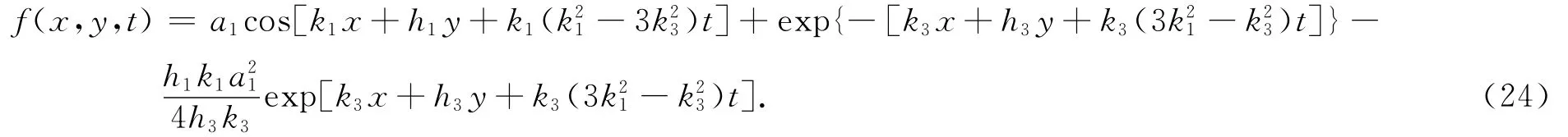
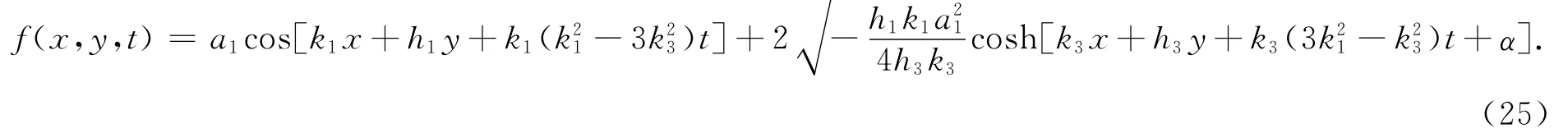
把式(2 5)代入式(2)得方程(1)的解为

其中ξ1=k1x+h1y+k1(k-3k)t,ξ3=k3x+h3y+k3(3k-k)t。

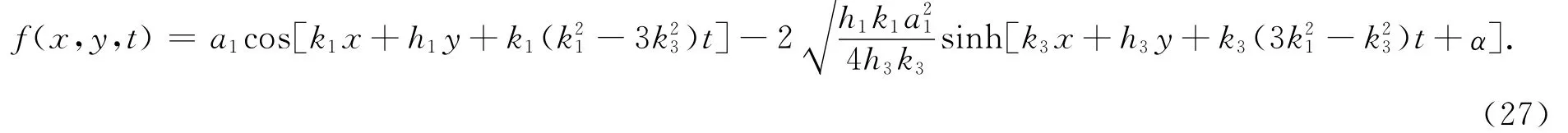
把式(2 7)代入式(2)得方程(1)的解为

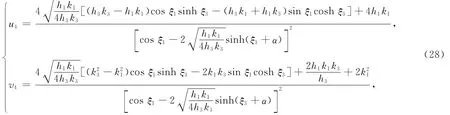
其中ξ1=k1x+h1y+k1(k-3k)t,ξ3=k3x+h3y+k3(3k-k)t。

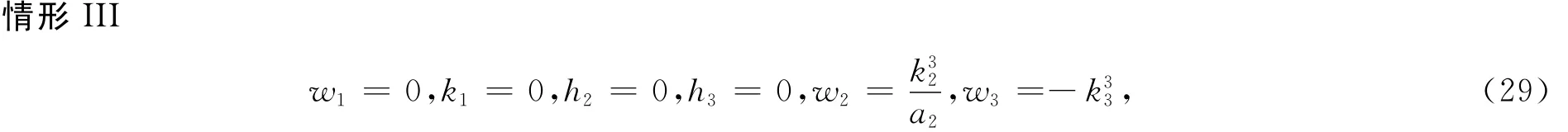
其中h1,k2,k3,a1,a2,a3为任意常数。把式(2 9)代入式(5)得

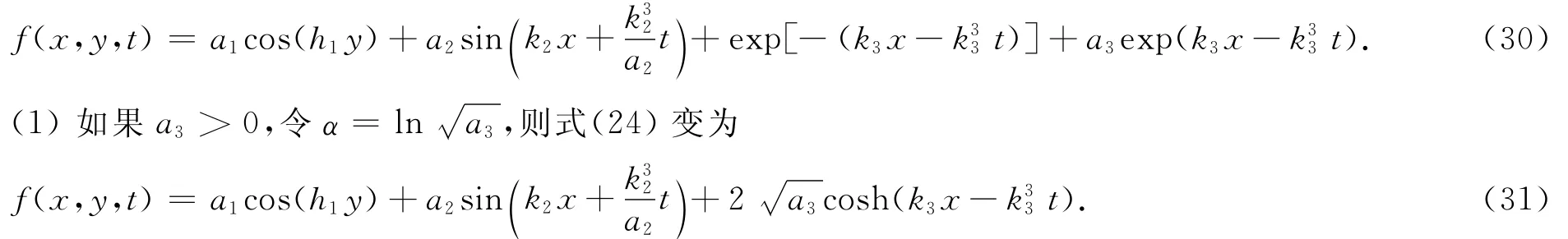
把式(3 1)代入式(2)得方程(1)的解为

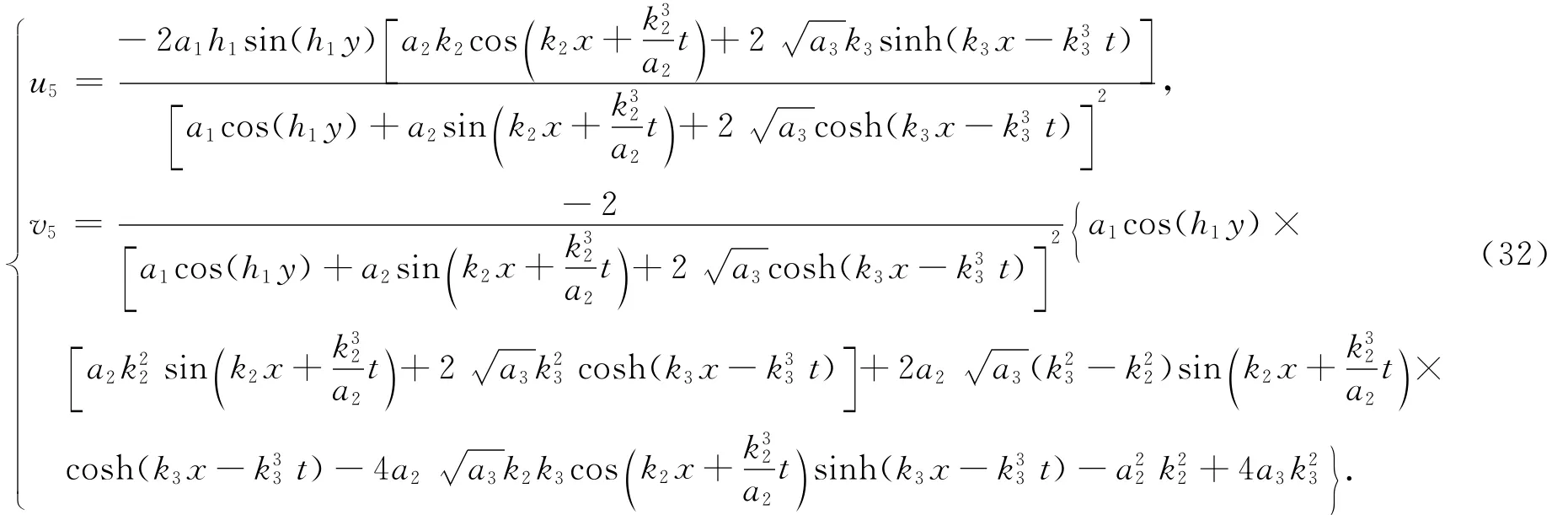
(2)如果a3<0,令α=ln,则式(24)变为

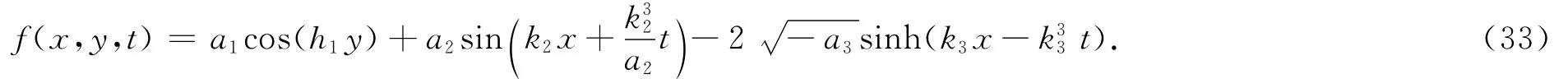
把式(33)代入式(2)得方程(1)的解为

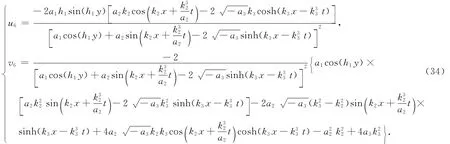
2 结论

本文扩展了Hirota法,即将Hirota法中的测试函数用新的测试函数来替代。以Burgers方程为例,给出用这个扩展后的方法求周期孤波解的具体过程,这些周期孤波解是新的。

[1]ABLOW ITZ M J,CLARKS ON P A.Soliton,nonlinear evolution equations and inverse scattering[M].Cambridge Univ.Press,1991:123-136.

[2]谷超豪.孤立子理论及其应用[M].杭州:浙江科技出版社,1990:86-98.

[3]MAT VEEV V B,S ALLEM A.Daroux transformations and solitons[M].Berlin:Sp ringer,1991:326-387.

[4]H I ROT A R.Exact s oluti on of the Korteweg-de Vries equation for multiple collisions of solitons[J].Phys Rev lett, 1971,27:1192-1194.

[5]楼森岳.推广的Painlevé展开及KdV方程的非标准截断解[J].物理学报,1998,47:1739-1745.

[6]傅海明.一类五阶KDV方程的行波解[J].鸡西大学学报,2008,8(6):143-144.

[7]WANGM L,ZHOU YB,LI ZB.Application of homogeneous balance method to exact solutions of nonlinear equations in mathematical physics[J].Phys LettA,1996,213:67-75.

[8]刘式适,傅遵涛,刘式达,等.Jacobi椭圆函数展开法及其在求解非线性波动方程中的应用[J].物理学报,2001,50 (11):2068-2073.

[9]傅海明,戴正德.一个(2+1)-维激光方程的孤波解[J].西北师范大学学报:自然科学版,2009,45(1):44-47.

[10]SALAN M,KAYA D.An application of the ADM t o seven-order Sawada-Kotara equations[J].App liedMathematics and Computati on,2004,157:93-101.

[11]LI JI BIN,ZHANG LI JUN.Bifurcations of traveling wave s oluti on in generalized Pochhammer-Chree equation[J]. Chaos,Soitons and Fractals,2002,14:581-593.

[12]HON Y C,FAN E G.Solitarywave and doubly periodic wave solutions for the Kersten-Krasil'shchik coupled KdV-mKdV system[J].Chaos,Solitons &Fractals,2004,19:1141-1146.