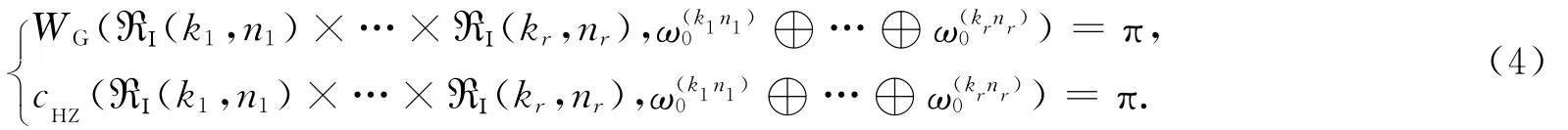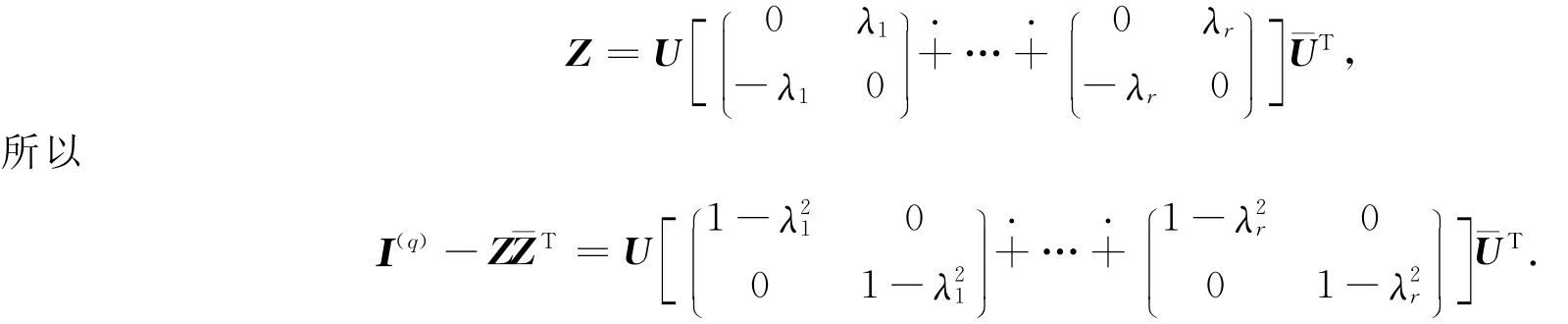四类典型域的Gromov辛宽度和Hofer-Zehnder辛容量
2012-12-13张巧,杨永
张 巧,杨 永
(郑州航空工业管理学院数理系,河南郑州450015)
一个2n维辛流形指的是一个2n维的流形M与其上一个非退化的闭2-形式ω组成的对(M,ω)。在一篇值得庆贺的文献[1]中,著名数学家Gromov引入了第一个非平凡的辛不变量——Gromov辛宽度WG。一个2n维辛流形(M,ω)的Gromov辛宽度定义为

这里B2n(r)={(x,y)∈R2n|x|2+|y|2 (单调性)若有辛嵌入φ:(M1,ω1)→(M2,ω2),则有WG(M1,ω1)≤WG(M2,ω2); (共形性)WG(M,cω)=|c|WG(M,ω)(这里c≠0)。 Gromov辛宽度WG是第一个非平凡的不变量。记Z2n(r)={(x1,y1)∈R2n 并由此得出了辛拓扑中著名的Gromov非挤压性定理。 Ekeland与Hofer受Gromov辛宽度WG性质的推动,文献[2]引入了辛容量的概念。一个辛容量是一个函子(funtor)c,它给每个辛流形(M,ω)指定了一个非负(可能无限)的数c(M,ω),并满足下面条件: (单调性)若有余维数为零的辛嵌入φ:(M1,ω1)→(M2,ω2),则c(M1,ω1)≤c(M2,ω2); (共形性)c(M,λω)=|λ|c(M,ω)(∀λ∈R{0}); (非平凡性)c(B2n(1),ω0)=π=c(Z2n(1),ω0)。 显然c的单调性意味着c是一个辛不变量。容易验证WG是第一个辛容量。 Hofer与Zehnder[3]引入了另一个重要的辛容量cHZ即Hofer-Zehnder辛容量。辛流形(M,ω)上一个光滑函数H被称为容许的(admissible),如果存在一个非空开子集U和一个紧致子集K⊂M∂M,使得: (b)0≤H≤max H; (c)M上哈密尔顿系统˙x=XH(x)没有非常值的周期小于1的周期解。这里XH定义为ω(XH,v)=d H(v)(v∈TM)。记Had(M,ω)为(M,ω)上的容许函数集。定义(M,ω)上的Hofer-Zehnder辛容量为cHZ(M,ω)≜sup {maxHH∈Had(M,ω)}。它与WG满足如下关系: 另外还有许多辛容量,它们是研究辛拓扑和哈密尔顿动力系统的重要的不变量,然而对辛容量进行计算和估计通常是很困难的。在文献[4]中,第一作者定义了拟辛容量的概念。特别的,他构造了Hofer-Zehnder型的典型的拟辛容量,并用这种拟辛容量计算出了许多辛流形的Gromov辛宽度和Hofer-Zehnder辛容量,详见文献[4]与[5]。对辛容量理论的历史与概况参见文献[4,6,7]及它们的参考文献。 典型域是多复变函数论和复几何中的一类重要的研究对象。四类典型域的矩阵表示[7]为 这里Z∈CmXn表示Z是m X n阶的复矩阵,¯ZT表示矩阵Z的共轭转置,以及H>0意味着H是一个正定的埃尔米特矩阵。 更一般地,由文献[4]中的引理4.1、引理4.2和式(22),立即可以得到 在主要定理的证明中将给出式(3)中“cHZ(ℜΙ(m,n),ω)≤π”的一个简单的证明。本文的主要结果是对另外三类典型域获得如下估计: 定理 注 (i)式(5)和(7)中的上界估计是最优的。事实上,当p=n=1时,ℜⅡ(1)=ℜⅣ(1)=B2(1),因为WG和cHZ都是辛容量,有 (ii)式(7)中的下界估计是最优的。由文献[7]中的引理2.1.3,线性映射 给出了ℜⅣ(4)与ℜⅠ(2,2)的一个线性同构。这里w1=z1+i z2,w2=z1-i z2,w3=i z3-z4,w4=i z3+z4。直接计算可得 式(6)的证明 设Z∈ℜⅢ(q),由引理3,若q=2r,则存在酉方阵U∈U(q)使得 类似的,若q=2r+1,则存在酉方阵U∈U(q)使得 若Z∈Bq(q-1)(1),则有 所以λi<1(i=1,…,r),从而可得Z∈ℜⅢ(q),因此有 同样,由式(8)知 类似上面式(5)的证明,式(6)可以从式(11)与(12)如下推得 式(7)的证明 设Z∈ℜⅣ(n),则 所以|Z|2-1<0,即Z∈B2n(1)。因此 注意到 从式(14)和(15)可以得出Z∈ℜⅣ(n),故 由Gromov辛宽度的共形性及式(1)有 类似上面式(5)和(6)的证明,理想的式(7)可以立即从式(13)、(16)和(17)推出。 [1]Gromov M.Pseudoholomorphic curves in symplectic manifolds[J].Invent.Math.,1985,82:307-347. [2]Ekeland I,Hofer H.Symplectic topology and Hamiltonian dynamics[J].Mathematische Zeitschrift,1989,200:355-378. [3]Hofer H,Zehnder E.A new capacity for symplectic manifolds[M].New York:Academic Press,1990:405-429. [4]Lu G C.Gromov-Witten invariants and pseudo symplectic capacities[J].Israel Journal of Mathematics,2006,156:1-63. [5]Lu G C.Symplectic capacities of toric manifolds and related results[J].Nagoya mathematical Journal,2006,181:149-184. [6]Gin Zburg V L.The Weinstein conjecture and the theorems of nearby and almost existence[J].Progr.Math.,2005, 232:139-172. [7]陆启铿.典型流形与典型域[M].上海:上海科学技术出版社,1963.

1 主要结果及主要定理的证明