氮化硼纳米管热输运性能的分子动力学模拟

高宇飞 孟庆元 张 璐 刘甲秋 荆宇航,*

(1哈尔滨工业大学航天学院,哈尔滨150001;2中国医科大学,沈阳110001;3哈尔滨玻璃钢研究院,哈尔滨150001)

氮化硼纳米管热输运性能的分子动力学模拟

高宇飞1孟庆元1张 璐2刘甲秋3荆宇航1,*

(1哈尔滨工业大学航天学院,哈尔滨150001;2中国医科大学,沈阳110001;3哈尔滨玻璃钢研究院,哈尔滨150001)

采用基于声子散射理论的Boltzmann-Peierls声子传输方程(BTE)和非平衡态分子动力学模拟(NEMD)方法研究了氮化硼纳米管(BNNT)的热输运性能.分析了BNNT的热力耦合效应,通过BTE与NEMD两种方法相结合,分析了温度和长度对BNNT热输运性能的影响,并应用量子修正扩大了NEMD的研究范围.结果表明:随着拉伸或压缩应变的增加,BNNT热输运性能均呈降低的趋势.通过计算声子态密度(PDOS)在理论上分析了以上结果,发现在拉伸状态下,声子模式的变化是决定BNNT热输运性能变化的主要因素;在压缩状态下,热导率变化是由于模型发生明显的屈曲变形引起的.在低温段,BNNT的热输运性能受量子效应影响最初有一个线性增加的过程,当温度超过一定值时,其开始显著地降低;当BNNT长度小于120 nm时,随着长度的增加,其弹道性能逐渐减弱,但仍主要体现为弹道特征,其热导率(κ)与长度(L)基本满足κ∝Lα这一关系.

氮化硼纳米管;热输运性能;Boltzmann-Peierls声子传输方程;非平衡态分子动力学模拟;声子态密度;量子修正

1 引言

纳米材料因其独特的结构和优良的力学、电学、热学、光学等性能,表现出广阔的应用前景.至1991年发现碳纳米管(CNT)以来,1各种不同种类的纳米管相继被发现,对它们的研究也随之展开.

1994年Rubio等2预测到一定存在氮化硼纳米管(BNNT).之后人们在实验中得到了多壁BNNT. 1996年Loiseau等3采用电弧放电法得到了单壁BNNT.有关BNNT及氮硼化合物的研究,如电子结构和力学性能的研究已经展开,4但有关其热学性能的研究却较少,在力学和热学交叉领域,如热力耦合效应方面还未见报道.BNNT作为一种典型的纳米材料,它的很多结构参数都对其热导率,尤其是轴向热导率有着显著的影响,5因此,可以利用BNNT的这种优良特性制成可控制的导热设备,这与传统的通过选择不同的材料来实现对器件导热性能控制的方法相比有了革命性的突破.因此有必要对BNNT的热传导机理和导热性能进行系统的研究.

目前针对BNNT导热性能的研究成果指出:对BNNT的热输运起主要贡献的是声子,这与CNT的热输运机理不同(对CNT热导率起主要作用的是声子和电子).BNNT的热导率低于CNT,但BNNT比CNT有着更强的热稳定性和化学稳定性;Liew和Yuan6通过分析CNT和BNNT混合物发现,BNNT具有更好的稳定性,较之CNT更适宜做管状结构的外壁;然而也有部分研究7指出,在低温段,BNNT的热导率要高于CNT.此外,同位素对BNNT热导率有着显著的影响,Zettl等8,9的研究指出,当BNNT中含有高浓度的B同位素时,其热导率可与CNT相比;纯的11B同位素可将BNNT热导率提升50%;10而Barman11的研究表明,同位素10B会削弱氮化硼晶体的热导率.BNNT具有较好的导热性能,在室温下,外直径为30-40 nm的BNNT的热导率可达到350 W·m-1·K-1;Stewart等12通过计算表明(8,0) BNNT的热导率为200 W·m-1·K-1.Nakayama等13发现氮化硼纳米带可以增强部分金属氧化物的导热性能.Mingo和Broido14通过研究输运方程和弹道函数发现纳米管的热传导性能表现出弹道特征.以上结果表明:BNNT在扫描探针显微镜、原子力显微镜的针尖,高温陶瓷以及纳米尺度热量计和微电子处理器等方面有着很大的潜在应用.但由于实验测量中的实际困难和材料在纳米尺度下的误差,目前理论和实验针对纳米管导热性能的定量研究结果具有较大的差别,如有部分研究结果15,16表明BNNT具有极低的热导率(热导率约1.5-14 W·m-1·K-1).总体来说,目前对于BNNT热输运机理和性能的定量研究成果仍很缺乏,而且随着声子散射理论的逐步完善,一些对BNNT导热性质产生重要影响的较复杂的因素,如纳米管的弹道传输与扩散传输的分界性能、应变作用下动态纳米管结构的热输运性能等逐渐被提出,并逐渐成为研究的热点.

本文首先采用非平衡态分子动力学模拟(NEMD)方法研究了BNNT在轴向应变作用下的热输运性能,并通过计算声子态密度(PDOS)的方法对模拟结果进行了理论上的补充和验证.进一步通过求解Boltzmann-Peierls声子传输方程(BTE)和NEMD相结合的方法分析了温度和长度对BNNT热输运性能的影响,通过量子修正扩大了NEMD的研究范围.为研究BNNT弹道传输与扩散传输的分界以及动态纳米管结构的热输运性能提供了一些理论与计算模拟的参考数据.

2 计算模型与方法

2.1 非平衡态分子动力学模拟方法

本文在模拟过程中应用Tersoff多体势17来描述BNNT中原子间的相互作用.求解原子的运动方程时采用预测—校正算法,积分步长为0.5 fs.边界条件选择为自由边界条件.构建BNNT模型时,首先根据BNNT的空间结构特点得到其初始构型的空间排列,然后将BNNT的初始构型在0 K下弛豫50000步,随后逐渐升温,每次升温100 K,并弛豫相同的步数,直到温度升到1600 K,最后进行退火处理来得到其稳定结构.

计算模型的热导率采用NEMD,18其基本思想为:将BNNT沿轴向等分为N层,设0层和N/2层为“冷区”和“热区”(见图1).每隔一定步数提取0层中动能最大的原子和N/2层中动能最小的原子,并交换两者速度.一般情况下冷区中动能最大的原子的动能大于热区中动能最小的原子的动能,这样便产生了一个从0层到N/2层的热流.又因为热区的温度高于冷区的温度,因此便存在一个与热流方向相反的温差.基于上述模型,经过统计可获得轴向各层的温度,进一步计算可得温度梯度(▽T),再结合能量交换过程中统计得到的热流密度(J),由Fourier导热定律J=-κ∇T,可计算得到BNNT的热导率(κ).整个非平衡态分子动力学模拟过程是通过Lammps开源软件包19实现的.

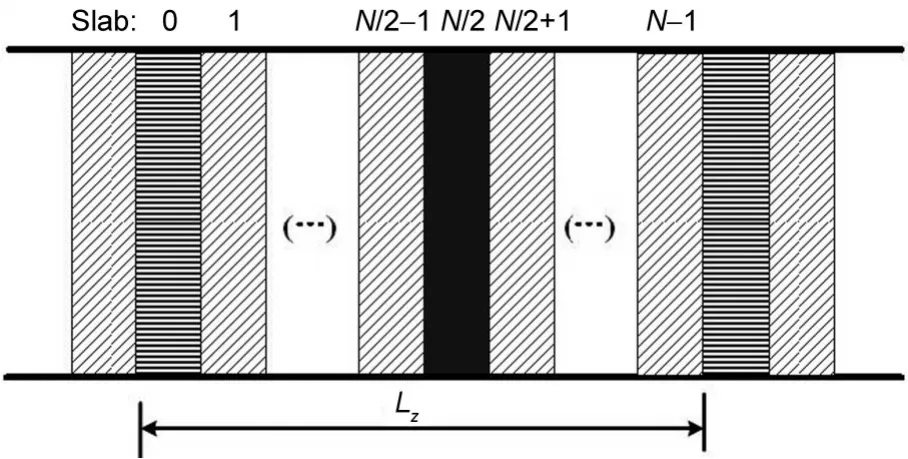
图1 非平衡态分子动力学模拟过程示意图Fig.1 Schematic diagram of NEMD process

图2为BNNT在300 K温度下轴向方向的温度分布图,其中各层温度是通过统计各层中所有原子的动能,通过公式(1)获得

其中N为层中的原子数,T代表温度,kB为Boltzmann常量,mi和vi分别为模型中i原子的质量和速度.从图中可发现中间各层的温度呈线性分布,而在冷层和热层附近区域,则有明显的非线性温度响应,这是由于热源和热槽的强相互作用产生的.20因此在计算BNNT热导率过程中,需要统计中间各层的温度,进而获得BNNT轴向方向的温度梯度以及热导率.

图2 BNNT轴向(L)的温度分布Fig.2 Temperature distribution of BNNT along axial direction(L)

模拟的整个过程分为五步:首先用Conjugate Gradient(CG)方法弛豫整个构型,以获得BNNT的稳定结构;然后将纳米管两端固定,在NPT系综下运行10000步(5 ps)标定压力使其处于最小状态;再在最小压力状态下运行100000步(50 ps),使系统达到稳定状态;然后在NVT系综下运行200000步(100 ps)来弛豫整个系统;最后在NVT系综下运行1000000步(500 ps)统计热流密度和温度梯度,计算得出BNNT的热导率(在最后一步过程中每100000步统计一次热导率,通过计算10个热导率数值的偏差分布可获得模型热导率的不确定度).

2.2 Boltzmann-Peierls声子传输方程方法

微观固体中的热量主要是靠晶格振动产生的声子传输的,声子是一些被抽象出的离散粒子,单一声子的能量为ℏω,ℏ=h/2π,h为普朗克常量,ω为频率.Boltzmann-Peierls声子传输方程14,21(BTE)可以完整地描述固体中声子间的相互作用.但获得BTE的精确解是困难的,目前可以通过一些近似的方法来获得不同模型对应的BTE的近似解.求解BTE的基本思想是通过不同声子的散射时间和处于非平衡态声子的分布,并结合模型的边界条件来获得模型热流与温度梯度,最后求得模型的热导率.

2.3 低温段量子修正

一般情况下,经典分子动力学模拟(MD)方法在温度接近和高于德拜温度时被认为是有效的,因为在此温度区域内所有的声子模式都被完全激发出来.与此相对的,当温度显著地低于德拜温度时,大量的声子没有被激发,模型的量子效应不能被忽略,此时经典的MD方法无效.为突破这一限制,量子修正方法(QCs)22-25被提出,目前它被广泛应用于热力学和力学的研究中.

QCs的基本思想是由经典力学系统中的模拟温度来计算量子系统中对应的修正温度,根据经典力学系统与量子系统能量相等,具体为系统的动能等于声子能量的一半这一原则.模拟温度(TMD)与修正温度的关系可表示为

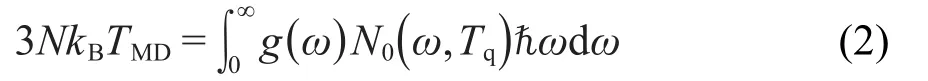
其中,N0为平衡态声子分布函数,Tq为量子修正温度,g(ω)为声子态密度.结合模拟中获得的TMD可计算Tq.通过统计不同时间的轴向热流密度和温度梯度,可获得修正后的热导率.

除了基于MD的QCs修正外,还存在两种基于势函数的量子修正方法,Feynman-Hibbs势函数(FH势)和Wigner-Kirkwood势函数(WK势)方法.FH势是由量子均分方程的Feynman-Hibbs估算变量获得的,是一种依赖于温度的二体势,可以方便地植入分子动力学或蒙特卡罗算法的计算程序中.应用这种方法,Sese26计算了Lennard-Jones系统的热力学和结构特性,Tchouar等27应用由FH方法演化的Lennard-Jones势研究了氖的热力学、结构和传输特性,Goharshadi等28应用Hartree-Fock dispersion近似势函数和FH势研究了氦的热力学性质.WK势是由对均分方程中德布罗意波长的扩展获得的,可以被用来研究不同物理特性系统的量子效应.

3 计算结果与讨论

3.1 热力耦合效应

本文选取20 nm的20_20扶手椅型BNNT(原子数为6320个)为研究对象,分别对模型施加在0-0.1范围的轴向拉伸和压缩应变.施加位移载荷过程中,应变是通过重新标定模型轴向原子坐标实现的,具体为首先选择BNNT轴向方向最外部两层原子,分别对其施加反方向的轴向位移载荷,每施加完一次位移载荷让系统弛豫一定步数,使系统达到平衡状态.加载速率为每5000个步长施加0.0025 nm的位移.在此期间统计不同时间BNNT轴向方向的热流密度和温度梯度,最终计算得到热导率随应变变化趋势如图3所示.由图3可发现,在拉伸和压缩应变作用下,BNNT的轴向热导率随着应变的增加而逐渐减小.

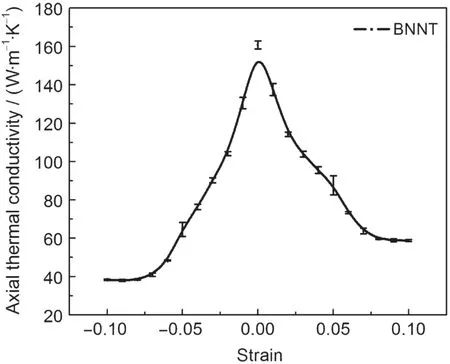
图3 BNNT轴向热输运性能随轴向应变的变化曲线Fig.3 Variation curve of axial thermal conductivity of BNNT under axial strain

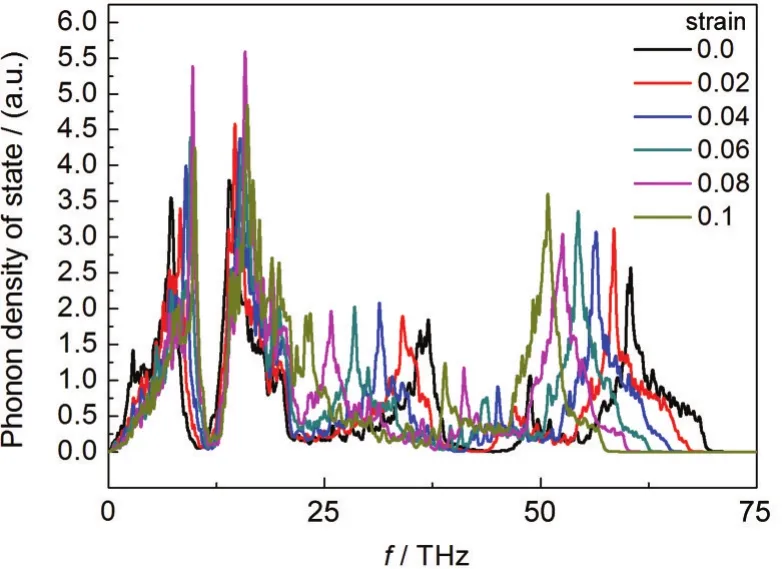
图4 BNNT在轴向拉伸应变作用下的声子态密度图Fig.4 PDOS of BNNT under axial tensile strain

声子态密度(PDOS)可以完整地描述各种模式声子的分布,可用于研究动态结构材料的热输运性能.PDOS是通过对速度自相关函数进行傅里叶变换得到的.29-32速度自相关函数可以表示为

其中

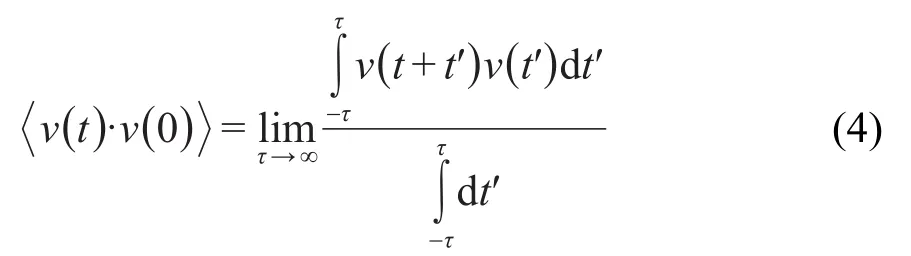
对(4)式进行傅里叶变换可得到PDOS的表达形式为

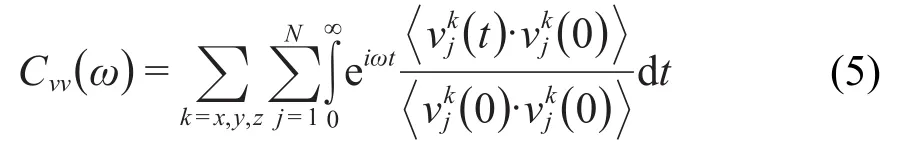
其中t代表时间,k=x,y,z代表模型的三个方向.通过上式,结合MD中统计的原子速度,可以获得不同应变作用下BNNT的声子态密度分布图.BNNT在拉伸和压缩应变作用下的声子态密度分布如图4、 5所示.

图5 BNNT在轴向压缩应变作用下的声子态密度高频波峰图Fig.5 High frequency peak in PDOS of BNNT under axial compressive strain

由图4可见,PDOS中有三个较高的波峰,其中前两个位于低频段,可被视为代表低频声子模式的波峰,后一个位于高频段,被认为是代表高频声子模式的波峰.随着应变的变化,相比于高频波峰,两个低频波峰的变化较小.这意味着高频声子对应变更加敏感.由于波峰的变化直接反映了声子数量的增加或减少,以及振动模式的增强或减弱,对比图4和图3我们可以发现,高频波峰的左移趋势伴随着模型热导率的下降,因此可以认为高频声子对模型热输运性能有着主要影响.

在0-0.1的拉伸应变作用下,随着拉伸应变的增加,从图4可以看出高频声子波峰逐渐左移.这意味着高频声子数量逐渐减少,部分高频声子逐渐转化为低频声子,它将导致声子的平均频率降低,因此此过程可以视为一个红移过程.Xu和Buehler33研究CNT在轴向应变作用下的热输运性能,发现红移过程将会减小声子的速度.在声子的弹道输运过程中,模型的热导率(κ)与声子速度有以下关系

其中c为比热,l为平均自由程,v为声子速度.因此图4中高频声子的变化趋势将导致BNNT的热导率随着拉伸应变的增加而逐渐减小.观察图5可以发现,在压缩应变作用下,不同应变的PDOS变化较小,几乎没有明显的变化.结合图6中0.1的拉伸和压缩应变作用下BNNT的构型图可以发现,在0.1的拉伸应变作用下BNNT被逐渐拉长,但其没有显著的塑性变形,而在0.1的压缩应变作用下,BNNT发生了严重的塑性变形.随着明显的塑性变形的产生,系统的能量将显著降低,进而导致模型中声子平均速度的降低,根据公式(6),在压缩应变下, BNNT的热导率随着应变的增加而逐渐减小.这也说明了在压缩应变下BNNT的热导率发生变化的机理不同于拉伸应变下的情况:在拉伸应变下,是声子模式的变化导致了BNNT热导率的变化;在压缩应变下,是BNNT结构的显著变化导致了其热导率的变化.

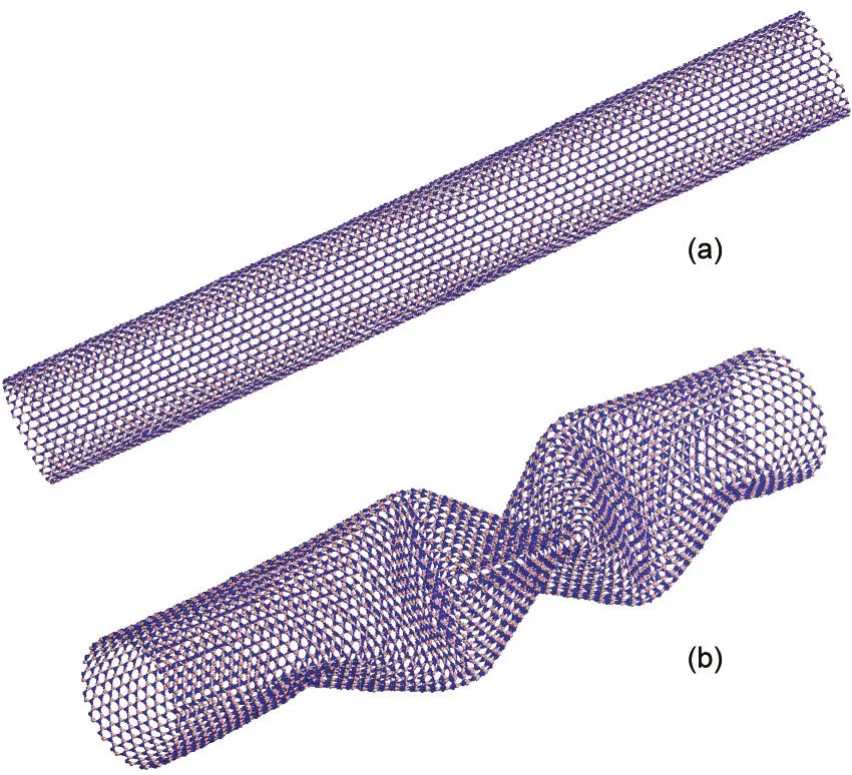
图6 BNNT在(a)0.1的拉伸应变作用和(b)0.1的压缩应变下的构型图Fig.6 Structures of BNNT under(a)0.1 tensile strain and (b)0.1 compressive strain

Buehler33和Zhang32等分别研究了CNT在应变作用下导热性能,本文在拉伸应变作用下得到的PDOS与Buehler和Zhang的结果有着相同的变化趋势,高频声子波峰均随着拉伸应变的增加而逐渐左移.在压缩应变的作用下,Zhang计算了-0.02-0压缩应变下CNT的PDOS,发现其高频声子波峰有部分右移的趋势.本文认为此处的不同是由于CNT的抗压缩性能强于BNNT导致的.在-0.02的小压缩应变作用下CNT较之BNNT更不容易产生较大的塑性变形,因此CNT的能量减少将体现在声子模式的变化上,而BNNT的能量减少体现在结构的变化上.

3.2 温度影响

本文应用NEMD,结合低温段温度量子修正方法研究了10-1600 K温度范围内长度为20 nm的10_10扶手椅型BNNT(原子数为3160个)的导热性能.首先统计模拟过程中BNNT的温度TMD,结合公式(2),可获得量子修正温度Tq.量子修正温度Tq与模拟温度TMD的关系见图7.其中实线为Tq随TMD的变化曲线,虚线用来对比Tq随TMD的变化率,斜率为1.从图中可见在低温段,∇Tq/∇TMD远大于1,随着温度的升高,其值逐渐减小,当温度达到1000 K时,∇Tq/∇TMD≈1,这说明此时Tq与TMD的变化率一致.结合Tq,可获得BNNT的热导率随温度的变化趋势如图8所示.

从图8可以看出,BNNT的轴向热导率在低温段(10-70 K)随着温度的升高近似呈线性增长趋势;当温度超过一定值(近似为100 K)时,其热导率随着温度的升高逐渐降低.

在低温段,当系统温度远小于德拜温度时,由于温度较低,晶格振动较弱,被激发出的声子较少.因此在低温段,材料的边界对长波声子的散射(也即边界散射)是影响材料热导率的主要因素.随着系统温度的降低,具有低频率、长波长的声子在声子中的比重增加.根据声子理论,长波声子较易与边界发生散射,这就导致了声子平均自由程减小,由(6)式可知,热导率也随之减小,因此在低温段,BNNT的热导率随着温度的增加而增加.在高温段,晶格振动剧烈,散发出大量的声子,因此声子与声子间的相互碰撞即声子间的散射取代边界对长波声子的散射成为影响材料热导率的主要因素.随着温度的增高,声子数增多,声子间的碰撞概率增大,声子平均自由程减小,因此在高温段,BNNT的热导率随着温度的增加而逐渐减小.

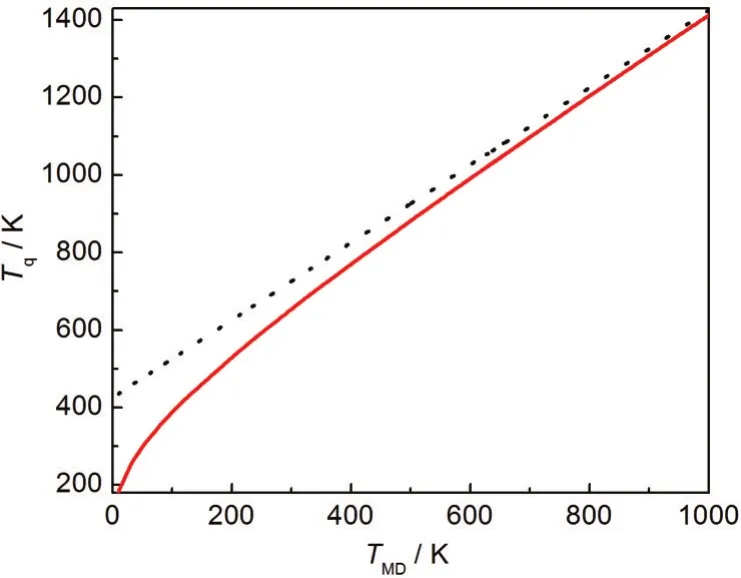
图7 模拟温度(TMD)与量子修正温度(Tq)的关系Fig.7 Relationship between simulated temperature(TMD) and quantum corrected temperature(Tq)The slope of dotted line is 1 and can be used to contrast the change rate of corrected temperature with simulated temperature.

图8 BNNT轴向热输运性能随温度的变化曲线Fig.8 Variation of axial thermal conductivity of BNNT under different temperatures

由图8还可观察到,在低温段,修正后的热导率与分子模拟直接获得的热导率有较大差别,随着温度的增加,这种差距逐渐减小.文献23对比了量子修正前后硅晶体的热导率变化曲线,当温度在800 K左右时,两者误差约为10%.本文用两种方法获得的数据误差为8%.文献34用MD计算了1200-2000 K下(10,10)BNNT的热导率,其热导率随着温度升高逐渐降低,且1200 K时BNNT热导率近似为48 W·m-1·K-1,1400 K时近似为43 W·m-1·K-1,1600 K时近似为38 W·m-1·K-1.计算得到上述三个温度的热导率分别为46、40、37 W·m-1·K-1,与文献34结果较为接近.文献35中通过理论分析BNNT的热导率随温度变化规律,发现几种直径(3,3)(5,0)和几种轴向长度(1,5,10 μm)的BNNT的热导率发生转折时系统的温度均在70-100 K范围内,而本文热导率发生转折的温度在70-90 K之间,这可从一个角度印证本文结果,可证明本文方法的正确性.

本文通过理论求解Boltzmann-Peierls声子传输方程得出了在低温段BNNT的导热性能与外界温度的关系.

BTE声子传输方程14可以表示为

左项描述声子漂移部分,右项描述声子散射部分,两项可分别表示为36,37

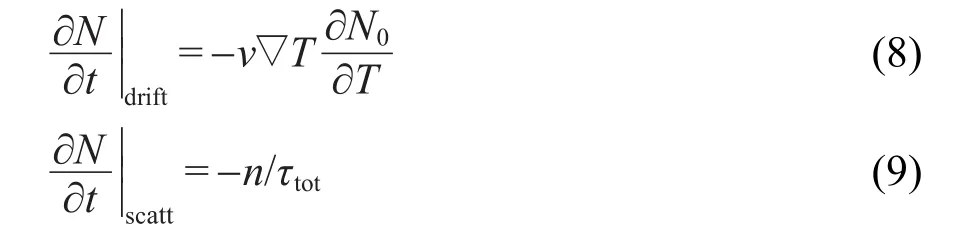
其中N为声子分布函数,N0为平衡态声子分布函数, n可表示为n=N-N0,它用来描述实际声子分布偏离平衡态的部分,τtot为总体弛豫时间,所以(7)式可以转化为

结合公式(10),热流可表示为

其中s为声子模式,q为波数,ω为频率.考虑热流和温度梯度的关系38

热导率可表示为

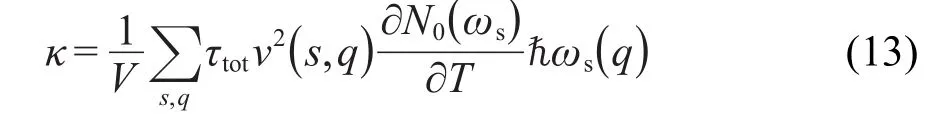
其中V为体积.在低温段,影响热导率的主要因素是声子与边界的散射,近似认为声子与边界的散射时间是散射时间τtot的主要部分.边界散射时间可表示为

其中p为描述边界粗糙程度的参数,Λ为描述材料横截面积的参数.

本文主要考虑边界散射对热导率的影响,可近似认为在低温状态下,τtot≈τb.并将公式(13)转化为相对于波数q的积分形式

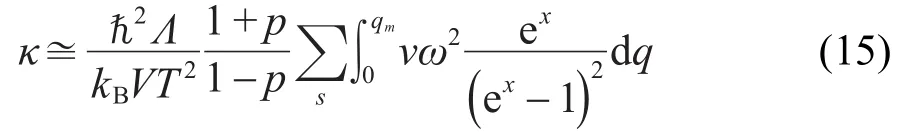
所以在低温段纳米管的热导率与温度符合κ∝T关系.

3.3 尺寸效应

根据声子散射理论,模型轴向长度的变化将因为其逐渐接近或者远离声子平均自由程而对声子在热输运过程中的散射产生影响,进而影响模型的热输运性能.本文建立了长度为10-120 nm的10_ 10扶手椅型BNNT,模拟温度选择为300 K,获得结果如图9所示.

如图9可知,BNNT的轴向热导率随着轴向长度的增加而增加,且增加的速率逐渐减小.

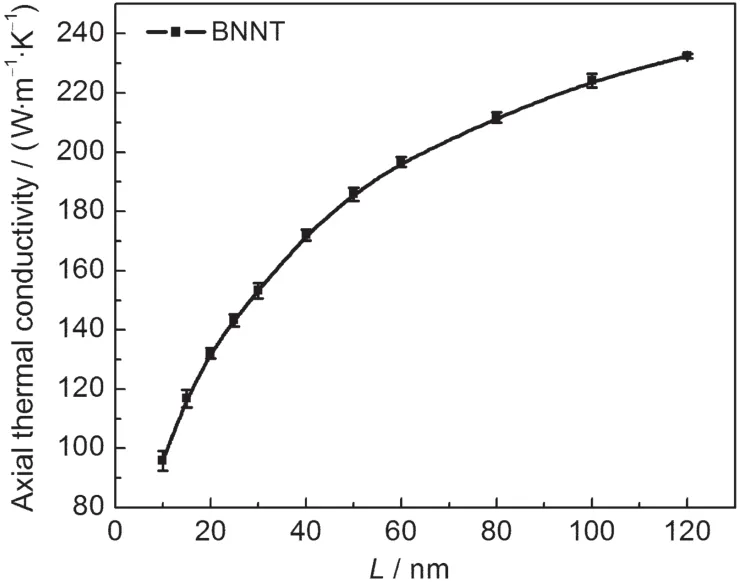
图9 BNNT轴向热输运性能与长度的关系Fig.9 Relationship between axial thermal conductivity and length

根据声子散射理论,随着BNNT轴向长度的增加,声子在传输过程中与边界的碰撞概率逐渐减小,这将增加声子平均自由程,根据公式(6),BNNT的热输运性能逐渐增加;随着BNNT轴向长度逐渐接近声子平均自由程,声子间相互碰撞概率逐渐增大,这对随着长度增加而逐渐减小的声子与边界的碰撞概率起到一个抵消作用,根据上文分析,BNNT的热输运性能增加趋势逐渐减缓.Mingo和Broido14通过计算CNT的BTE得到热导率与长度呈κ∝Lα这一关系,且随着L的增加,α值(描述模型弹道特性的参数)逐渐减小.本文通过MD获得的结果如拟合为κ∝Lα形式,其α值大致介于0.1989-0.4899之间,且随着长度的增加,α值逐渐减小,这与Mingo的理论结果相吻合.同时这也意味着随着BNNT长度的增加,模型的弹道性能逐渐减弱,但其仍主要体现弹道特征.

4 结论

运用NEMD研究了BNNT的热输运性能,分别研究了长度、温度和应变对BNNT的热输运性能的影响,并得到了以下结论:在拉伸应变作用下,随着应变的增加,受声子模式变化的影响,BNNT的热导率呈逐渐降低的趋势;在压缩应变作用下,随着应变的增加,受BNNT发生显著塑性变形的影响,其热导率逐渐减小.当外界温度低于70 K时,受量子效应的影响,BNNT的热导率随着温度的增加呈线性增加趋势;当温度高于100 K时,其热导率随着温度的增加而逐渐减小.当BNNT轴向长度小于120 nm时,随着长度的增加,其弹道性能逐渐减弱,但仍主要体现为弹道特征,其热导率与长度基本满足κ∝Lα这一关系.

(1) Iijima,S.Nature 1991,354,56.

(2) Rubio,A.;Corkill,J.L.;Cohen,M.L.Phys.Rev.B 1994,49 (7),5081.

(3) Loiseau,A.;Willaime,F.;Demoncy,N.;Hug,G.;Pascard,H. Phys.Rev.Lett.1996,76(25),4737.

(4) Wirtz,L.;Rubio,A.Phys.Rev.B 2003,68(4),045425.

(5) Zhang,G.;Li,B.W.The Journal of Physical Chemistry B 2005, 109(50),23823.

(6) Liew,K.M.;Yuan,J.H.Nanotechnology 2011,22,085701.

(7) Xiao,Y.;Yan,H.;Cao,J.X.;Ding,J.W.;Mao,Y.L.;Xiang,J. Phys.Rev.B 2004,69(20),205415.

(8) Chang,C.W.;Fennimore,A.M.;Afanasiev,A.;Okawa,D.; Ikuno,T.;Garcia,H.;Li,D.Y.;Majumdar,A.;Zettl,A.Phys. Rev.Lett.2006,97,085901.

(9) Chang,C.W.;Okawa,D.;Majumdar,A.;Zettl,A.Science 2006,314,1112.

(10) Zhi,C.Y.;Bando,Y.;Tang,C.C.;Golberg,D.Materials Science and Engineering R 2010,70,92.

(11) Barman,S.Europhysics Letters 2011,96,16004.

(12) Stewart,D.A.;Savic,N.;Mingo,N.Nano Lett.2009,9,81.

(13) Cho,H.B.;Tokoi,Y.;Tanaka,S.;Suematsu,H.;Suzuki,T.; Jiang,W.H.;Niihara,K.;Nakayama,T.Composites Science and Technology 2011,71,1046.

(14) Mingo,N.;Broido,D.A.Nano Lett.2005,5(7),1221.

(15) Chang,C.W.;Han,W.Q.;Zettl,A.Journal of Vacuum Science &Technology B 2005,23,1883.

(16) Tang,C.C.;Bando,Y.;Liu,C.H.;Fan,S.S.;Zhang,J.;Ding, X.X.;Golberg,D.The Journal of Physical Chemistry B 2006, 110(21),10354.

(17) Tersoff,J.Phys.Rev.B 1988,37(12),6991.

(18)Wang,X.W.;Huang,Z.;Wang,T.;Tang,Y.W.;Zeng,X.C. Physica B 2008,403,2021.

(19) Sandia National Laboratories.LAMMPS,Lammps-12Oct10; GNU:USA,2010.

(20) Schelling,P.K.;Phillpot,S.R.;Keblinski,P.Phys.Rev.B 2002, 65(14),144306.

(21) Lindsay,L.;Broido,D.A.;Mingo,N.Phys.Rev.B 2009,80, 125407.

(22) Wang,S.C.;Liang,X.G.;Xu,X.H.;Ohara,T.J.Appl.Phys. 2009,105,014316.

(23)Turney,J.E.;McGaughey,A.J.H.;Amon,C.H.Phys.Rev.B 2009,79(22),224305.

(24) Munoz,E.;Lu,J.X.;Yakobson,B.I.Nano Lett.2010,10(5), 1652.

(25) Hu,J.N.;Ruan,X.L.;Chen,Y.P.Nano Lett.2009,9(7),2730.

(26) Sese L.M.Mol.Phys.1993,78,1167.

(27) Tchouar,N.;Ould,K.F.;Levesque,D.J.Chem.Phys.2004, 121,7326.

(28) Goharshadi,E.K.;Abbaspour,M.;Kashani,H.;Baherololoom, M.Theor.Chem.Acc.2008,119,355.

(29) Yang,N.;Zhang,G.;Li,B.W.Nano Lett.2008,8(1),276.

(30) Kang,D.D.;Hou,Y.;Dai,J.Y.;Yuan,J.M.Phys.Rev.A 2009, 79,063202.

(31) Huang,M.J.;Weng,C.C.;Chang,T.M.International Journal of Thermal Sciences 2009,49,1095.

(32) Ren,C.L.;Zhang,W.;Xu,Z.J.;Zhu,Z.Y.;Huai,P. The Journal of Physical Chemistry C 2009,114(13),5786.

(33) Xu,Z.P.;Buehler,M.J.Nanotechnology 2009,20,185701.

(34) Shen,H.J.Computational Materials Science 2009,47,220.

(35) Jiang,J.W.;Wang,J.S.Phys.Rev.B 2011,84(8),085439.

(36) Goicochea,J.V.;Madrid,M.;Amon,C.ASME J.Heat Transfer 2010,132,012401.

(37)Chen,Y.F.;Li,D.Y.;Lukes,J.R.;Majumdar,A.ASME J.Heat Transfer 2005,127,1129.

(38) Nika,D.L.;Pokatilov,E.P.;Askerov,A.S.;Balandin,A.A. Phys.Rev.B 2009,79(15),155413.

November 30,2011;Revised:January 28,2012;Published on Web:February 27,2012.

Molecular Dynamics Simulation of Thermal Transport Properties for Boron Nitride Nanotubes

GAO Yu-Fei1MENG Qing-Yuan1ZHANG Lu2LIU Jia-Qiu3JING Yu-Hang1,*
(1School of Astronautics,Harbin Institute of Technology,Harbin 150001,P.R.China;2China Medical University, Shenyang 110001,Liaoning Province,P.R.China;3Harbin FRP Research Institute,Harbin 150001,P.R.China)

The Boltzmann-Peierls phonon transport equation(BTE)and non-equilibrium molecular dynamics simulation(NEMD)are used to investigate the thermal transport properties of boron nitride nanotubes(BNNTs).First,the thermal-mechanical coupling is explored using NEMD.Then,by combining BTE and NEMD,the influence of temperature and length is investigated.Quantum correction is used to extend the range over which NEMD can be used.The results demonstrate that under low-strain conditions,the thermal conductivity decreases with increasing tensile or compressive strain.Then the phonon density of state(PDOS)is used to analyze the trends in thermal transport properties theoretically; it is found that the variations in thermal transport properties under tension are caused by changes in the phonon modes,and that under compression changes are induced by the flection of the BNNT structure. The BNNT thermal conductivity increases linearly with increasing temperature because of the quantum effect at low temperatures,and it decreases significantly as the temperature reaches a certain value. When the BNNT length is less than 120 nm,the BNNTʹs ballistic characteristics weaken with increasing length,but it also performs ballistic characteristic mainly,and thermal conductivity(κ)and length(L)obey the relationshipκ∝Lα.

Boron nitride nanotubes;Thermal transport property;Phonon Boltzmann-Peierls transport equation;Non-equilibrium molecular dynamics simulation;Phonon density of state;Quantum correction

10.3866/PKU.WHXB201202273

∗Corresponding author.Email:jingyuhang@gmail.com;Tel:+86-451-86414143.

The project was supported by the National Natural Science Foundation of China(10772062).

国家自然科学基金(10772062)资助项目

O641;O642