用Excel进行威布尔型产品可靠性数值仿真评估
2012-12-10张仕念张国彬易当祥颜诗源杨艳妮
张仕念,张国彬,易当祥,颜诗源,杨艳妮
(北京市清河大楼子八,北京 100085)
0 引言
可靠性仿真是将仿真技术应用于可靠性分析的一种方法,利用计算机技术对己经建好的系统可靠性模型进行仿真,得到一系列的仿真结果,能够解决常规的解析法很难奏效的部分可靠性问题。可靠性仿真具有经济性好、应用范围广、通用性好、难度小、直观和保密等优点[1]。Microsoft Excel是微软公司开发的电子表格软件,易学易用,使用范围广;Excel 2003就提供了财务、日期与时间、数学与三角函数、统计等九大类约300个函数,具有强大的计算、统计功能。本文以服从威布尔分布的数据为例,利用Excel的、已有函数和单元格的引用,进行复杂的数值计算,利用RAND()函数产生的随机数而引入随机因素,实现可靠性评估的数值仿真。实例表明,用Excel进行可靠性评估的数字仿真,可以避免繁杂的编程工作,省时省力,方便实用,且仿真结果与计算结果十分接近。
1 威布尔型数据的可靠性评估模型
设n台产品进行无替换截尾试验,失效时间为t1≤t2≤…≤tr(r≤n), 定数截尾时 tr为第 r个产品的失效时间,定时截尾时tr为截尾时间,失效数据服从两参数威布尔分布。其密度函数为:
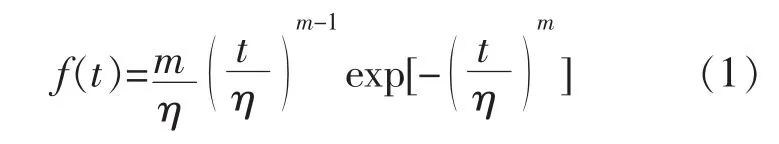
分布函数为:
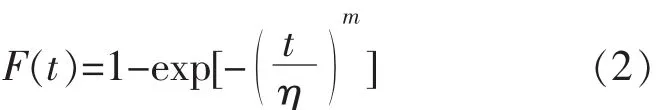
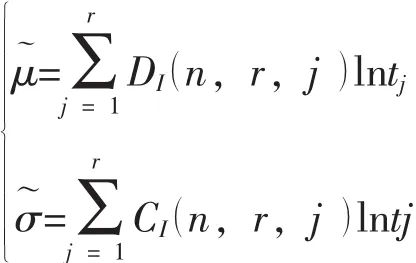
式中, DI(n, r, j ), CI(n, r, j)可查 《可靠性试验用表》[3]获得。
对给定的n,r,γ,R,Mann等给出了枢轴量:
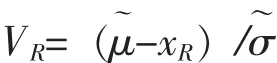
的γ分位数VR,γ数表,式中xR是极值分布的 (1-R)分位数,即

2 威布尔型数据的可靠性数字仿真
则tR的置信下限:
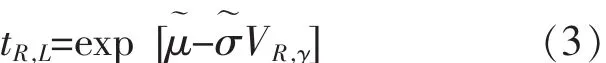
根据对称原理, 在式 (3) 中将tR,L→t0,R→RL(t0), 得可靠性下限 RL(t0) 的表达式为:
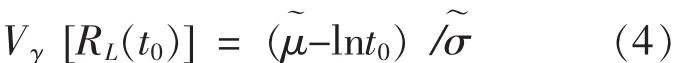
故可反查Vγ(R)-R表,用中转查值法可求出 RL(t)。
2.1 随机数的产生及随机变量抽样
目前,广泛应用的、在 [0,1]上产生均匀分布的伪随机数的方法是同余法[3],包括混合同余发生器、乘法同余发生器等。Excel提供的RAND()函数也能够产生 [0,1]的随机数,在其帮助中,说明该函数用于 “返回大于等于0及小于1的均匀分布随机数,每次计算工作表时都将返回一个新的数值”。用RAND()函数产生5次,每次5组, 每组 5000个随机数,用 Co(i,j) (i≠j)表示第i组和j组随机数的相关系数,随机数之间的相关系数见表1。由表1可见,其相关系数很小,表明各组随机数之间的独立性很好。本文用RAND()函数产生随机数。
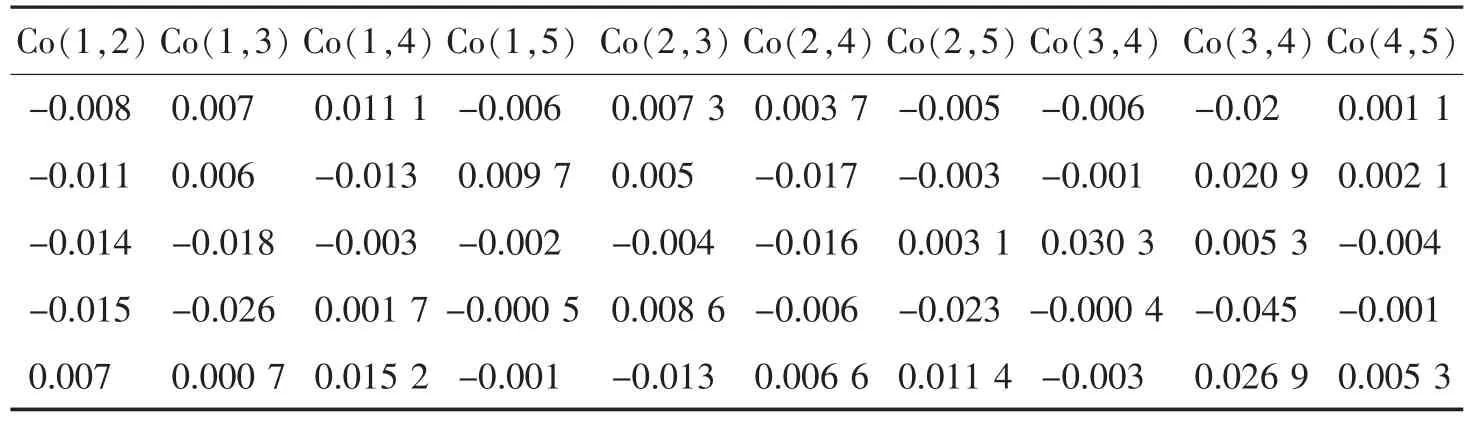
表1 5组随机数的相关系数
可采用逆变法[4]产生服从威布尔分布的随机数,具体的步骤如下:
a)在 (0,1)区间上产生服从均匀分布的随机数 r。
b)做变换。
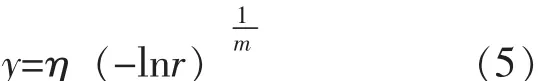
式 (5)中:y——服从参数为m,η的威布尔分布的随机数。
c)重复步骤a)、b),直到取到要求数量的随机数为止。
2.2 分布参数的最小二乘估计
由式(2) 得:
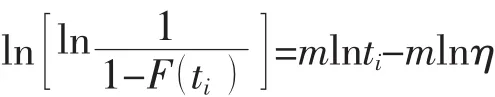
令
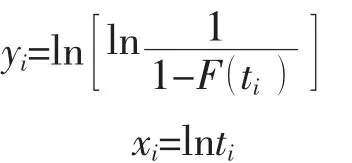
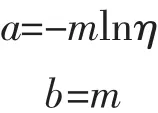
则
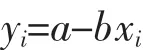
如果ti服从威布尔分布, {xi,yi}成线性关系,通过最小二乘法线性回归,解得系数a、b。
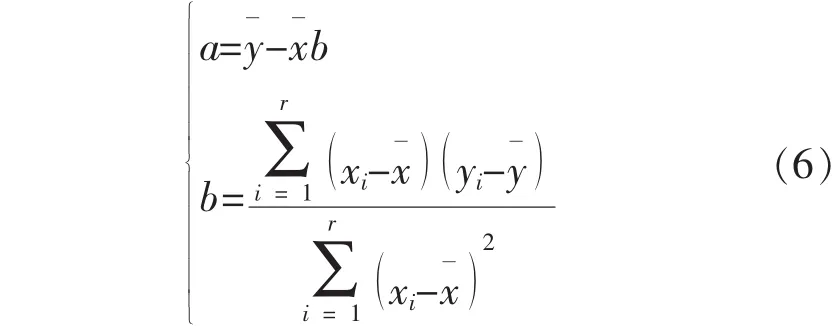
则
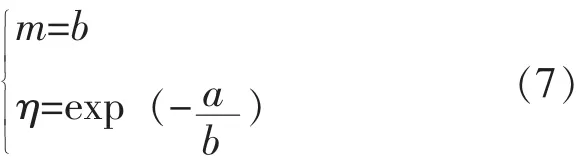
两个变量的相关系数表示为:
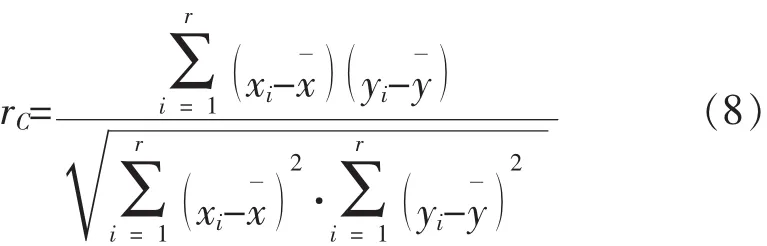
可根据|rC|→1的程度,判断是否服从威布尔分布。
在计算过程中,无替换定数截尾时,分布函数为:
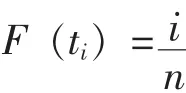
小样本 (n≤20)时,为了减少计算误差,用下式计算:
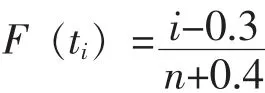
2.3 仿真步骤
数字仿真的基本思路是:用最小二乘法根据原始数据估计分布参数和,利用随机数发生器和逆变法抽取服从分布参数为和的威布尔分布的抽样样本,根据抽样样本计算出可靠度的一个抽样值,反复抽样,得到可靠度的分布密度函数,从而获得可靠度的置信下限。具体的步骤如下:
a)根据最小二乘法,利用Excel软件的单元格 引 用 和 LN (number)、 AVERAGE (number1,number2, ...)、 EXP (number) 等函数, 由式 (6)和 (7) 计算威布尔分布的分布参数m^和η^。
b)从仿真循环次数i=1开始,由式 (5),在Excel软件电子表格的某一列用 “=*POWER ((-LN (RAND ())),” 产生 r个服从威布尔分布的随机数;在另一列用 “=SMALL(array1,k)”(array1为r个随机数组成的数列,k=1,2,…,r)函数对其由小到大排序,得故障产品的抽样观察值为ti1,ti2,…,tir(无替换定时截尾时,产生n个服从威布尔分布的随机数,取定时截尾时间T0以前的样本排序)。
c)由故障产品寿命的抽样观察值ti1,ti2,…,tir,同a),采用最小二乘法估计抽样样本的分布参数为和。
d)对于给定任务时间t0,对应的可靠度抽样值为:
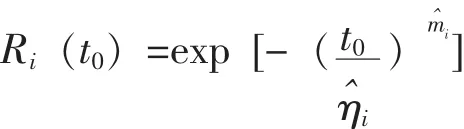
e)i=i+1重复上述过程,1≤i≤N,N为仿真次数。单元格引用和公式在Excel电子表格中建立后,只需做简单的拷贝即可完成。
f)给定置信度γ,在可靠度的分布密度函数中, (1-γ)N的整数部分对应的Ri(t0), 就是给定置信度为γ的可靠度下限值,即在某一单元格用 “=SMALL (array2,(1-γ)*N)” 的返回值即为仿真结果,此处的array2为仿真结果组成的数列。
给定可靠度R的可靠寿命tR的抽样公式为:
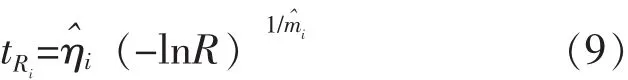
对tRi反复抽样,进行排序得tR1≤tR2≤…≤tRN,对于给定的置信度γ的寿命下限tR为 (1-γ)N的整数部分对应的tRi。
4 仿真算例
取某产品15台进行无替换定数截尾自然贮存试验,10台产品出现失效,失效时间分别为 (单位 : 年 ) :14.71、 15.09、 18.29、 19.91、 20.67、21.87、 22.32、 22.87、 24.91、 25.06。 给定置信度为0.75,求:a)给定可靠度R=0.95时产品的可靠寿命下限;b)任务时间t0=14年时的产品贮存可靠度下限。
采用最小二乘法估计以上数据的参数时,用式 (8)计算相关系数rC=0.977638,可以认为该产品的贮存寿命服从威布尔分布。查 《可靠性试验用表》获得n=15、 r=10 时的 DI(n, r, j)、 CI(n, r,j)。
现用Excel对其进行仿真,每次抽取4000个样本,仿真5次所得的结果见表2。由表2可见,5次仿真的可靠寿命的平均值为12.053,计算值为12.43,5次仿真的贮存可靠度的平均值为0.920,计算值为0.919,二者很接近。
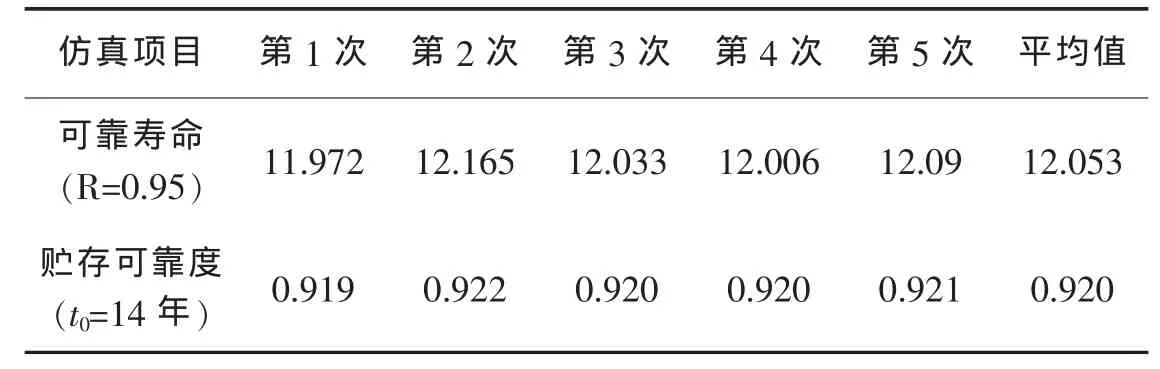
表2 某产品的可靠寿命、可靠度仿真结果
4 结束语
通过以上分析和实例可以看到,采用Excel进行可靠性数值仿真,只需利用Excel提供的函数和单元格的引用就可实现复杂的数值计算,简单直观,方便实用,仿真结果准确可信,对可靠性评估研究和可靠性分析计算具有重要的参考价值,有助于可靠性仿真技术的推广应用。
[1]陆胜勇.可靠性仿真技术 [J].电子产品可靠性与环境试验, 1999, (1): 19-22.
[2]周源泉.质量可靠性增长与评定方法 [M].北京:北京航空航天大学出版社,1997.
[3]中国电子技术标准化研究所.可靠性试验用表[M].增订本.北京:国防工业出版社,1987.
[4]宋笔锋.飞行器可靠性工程[M].西安:西北工业大学出版社,2006.
