一种基于马尔可夫模型的软件可靠性评估方法

刘志祥，刘杰，李丹，云雷

（工业和信息化部电子第五研究所，广东 广州 510610）

0 引言

软件可靠性的研究起源于Hudson等人的工作，早期的研究主要针对软件测试和现场运行阶段收集的软件失效数据，建立可靠性增长模型。对于软件可靠性模型 （SRM：Software Reliability Model）发展首次起到较重要作用的两个模型，发表于1971年。Shooman模型由M.L.Shooman发表，J-M模型由Z.Jelinski和P.B.Moranda发表。到80年代末，可靠性增长模型的研究达到高潮[1-7]。

SRM的研究在20世纪70年代获得较大的发展后，很多可靠性模型已经投入使用。可以说，软件可靠性建模己经从研究阶段发展到了工程阶段。国内外已提出100多种软件可靠性评价模型，其中以J-M模型、G-O模型、Musa执行时间模型、LV模型和Seeding模型等为典型代表[8-10]。David、Howden、Parnas等人提出了基于经典统计假设理论的测试方法，为安全关键软件的可靠性测评奠定了取样理论基础；而Little wood、Miller等人提出了基于Bayesian统计理论的测试方法。为了改善测试用例开销，Bojan Cukie提出了结合形式化证明和程序动态测试的转换方法。自1972年第一个软件可靠性分析模型发表后的20多年以来，见之于文献的SRM有近百种，与每个模型相应的假设又有几条甚至几十条。这些可靠性模型大致可分为种子法、失效率类、曲线拟合类、可靠性增长模型、程序结构分析模型、输入域分类模型、执行路径分析方法模型、非齐次Poisson过程模型、马尔可夫过程模型和贝叶斯模型等10类[11-14]。

SRM所要解决的问题有两个：改进软件开发过程和软件可靠性的度量。相应地，针对可靠性模型及其应用展开的研究主要集中在两个方面：1）关于软件可靠性早期预测模型的研究；2）关于软件可靠性预测模型的研究。其中，早期预测模型是指在不知失效数据的情况下，根据软件产品及其开发过程来度量、预测软件可靠性；这种模型对于改进软件开发过程、指导软件测试、提高软件可靠性具有重要意义。可靠性预测模型则着眼于未来，对软件的可靠性进行预计，预计软件当前失效强度、下次失效时间等。文献 [15]在基于模糊神经网络的基础上，提出了一种新的软件可靠性早期预计方法。通过分析软件缺陷产生的原因，给出了导致软件缺陷产生的因素。同时，深入讨论了软件可靠性早期预计的建模方法。文献 [16]依据软件可靠性特征，提出以解决软件开发逻辑思维正确性为建模基本问题的可靠性建模思想。为了在不降低安全关键软件可靠性验证测试结果可信性的前提下减少测试用例量，文献 [17]在分析经典统计假设测试和无先验贝叶斯统计方法的基础上，提出了一种先验知识动态整合的贝叶斯推断统计测试方法。文献[18-19]基于马尔可夫链描述软件系统控制转移的动态特性，研究了基于马尔可夫链 （MC：Markov Chain） 分 析方法 ， 以 及 随 机 Petri网 （SPN：Stochastic Petri Nets）、 失效相关性 （Failure Correlation)的可信软件的可靠性建模问题。系统在长期运行一段时间后会出现系统性能下降或停机的现象，这种情况被称为软件老化 （SA：Software Aging）。为了抵消软件老化造成的影响，Yennun Huang等提出了软件再生 （SR：Software Rejuvenation）技术。这是一种预防性的软件容错策略，能有效地提高软件系统的可靠性和可用性。目前看来，要建立比较适用的SRM，必须改变传统的可靠性建模思路，采用新的观点、方法和新的数学工具来研究软件故障过程。

由于目前国内外软件可靠性建模主要是对整个软件系统进行可靠性建模分析，而按照软件运行流程进行状态分析的可靠性建模考虑得较少。本文摆脱传统模型多种主观假设的束缚，尝试以软件运行流程的状态为研究对象，结合软件运行流程特点，将基于统计测试的方法与软件运行流程联系起来，结合马尔可夫理论等工具进行可靠性建模研究。

1 马尔可夫模型

由时刻t0系统或过程所处的状态，决定系统或过程在时刻t＞t0所处的状态，并不需t0时刻以前系统或过程所处状态的历史资料，这类确定性现象在物理学中出现频繁。依照上述规律，当一物理系统或过程遵循的是某种统计规律时，可引入以下特性：

t0时状态已知，时刻t（t＞t0）的状态只与该过程在t0时刻的状态有关，而与其在t0时刻以前所处的状态无关，这种特性被称为无后效性或马尔可夫性。用分布函数表述马尔可夫性如下：

a） 定义 1， 设随机过程 {X （t），t∈T}的状态空间为I。如果对时间t的任意n个数值 t1＜t2…tn， n ≥3， ti∈T， 在 条 件 X （ ti） =xi， xi∈I， i=1，2，…，n-1下，X （tn）的条件分布函数恰等于在条件X （tn-1）=xn-1下，X （tn） 的条件分布函数，即

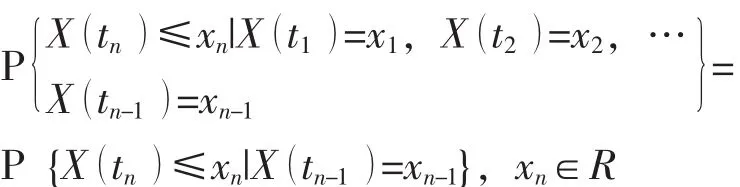
这个过程为马尔可夫过程。

设随机过程 {Xn，n∈T}，其参数集T是离散的时间集合，即T={0，1，2…}，其相应xn可能取值的全体组成的状态空间是离散的状态集I={i1，i2， i3…}。

b）定义2，若对于任意的整数n∈T和任意的i0， i1， i2…in+1∈I， 条件概率满足

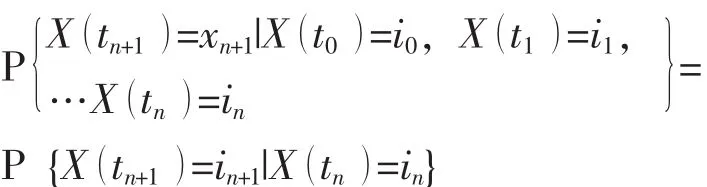
则称 {Xn，n∈T}为马尔可夫链。

马尔可夫链是一种以统计理论为基础的统计模型，在软件统计测试中得到了广泛的应用。它是一种迁移具有概率特征的有限状态机，可以根据状态间迁移概率自动生成测试用例，还可以分析结果，对软件性能指标和可靠性指标等进行度量。另外，Markov链模型适用于对多种软件进行统计测试，它的产生基于软件规范而不是程序代码，它可以和软件开发同时进行，并可以通过仿真得到状态和迁移覆盖的均期望时间，有利于在开发早期对大规模软件系统进行测试费用和时间的规划。

由马尔可夫链描述的软件使用模型可以用随机迁移矩阵或者带迁移概率的状态迁移图表示。用状态迁移图表示的优点是直观易懂，通常只用于小型系统或大型系统的高端表示。用随机迁移矩阵表示，行和列代表状态，矩阵的单元值代表状态间转移概率。此种方法的优点是较容易描述复杂系统，但不够直观。

一个测试用例就是一个文档，描述输入、动作或者时间和期望的结果，其目的是确定应用程序的某个特性是否正常工作。一个测试用例应该有完整的信息，如：测试用例ID号、测试用例名字、测试的目的、测试条件、输入数据需求、步骤和期望结果。

在基于使用模型的测试中，所有用例的目的，宏观来讲，就是看软件在某一状态得到激励后，是否能转向预期的下一状态，每一状态转换所代表的具体功能宏观上不予考虑。测试条件是指软件的当前状态，输入数据需求则是当前状态所对应的激励，期望结果则是正确地转换至下一状态。因此，在基于使用模型的测试用例生成中，一个测试用例是一个状态、激励序列。

基于马尔可夫模型的统计测试方法按照充分性的测试用例原则，只能解决一部分的状态概率问题，同时目标的可靠性计算方法需要更加详细的理论依据，本文提出一种可靠性评估模型和方法，试图解决这个问题。

2 可靠性评估模型和方法

任何的软件都会依照系统设计流程图来编写，每个流程图都会有该软件所对应的状态。假设某一个复杂软件中有 n个正常状态，设为 A1，A2，……An，该软件有1个异常状态，在这个状态下软件功能失效，设为Q，同时加上开始状态和终止状态，则可以为该软件建立一个状态转移模型，如图1所示。

软件的每一次运行流程都从Begin开始，经过若干个中间状态，最后到达Exit状态。每一状态转移对应一次输入，即一次激励。由于模型中可能有循环，可能会产生无穷序列，所以输入序列可以通过遍历状态转移图来得到。利用Markov链使用模型，便可以获得大量的输入序列。一个测试输入，就是根据Markov链使用模型从输入域中随机产生的一个有限输入序列。由图1看出，软件的状态转移从Begin开始，经过输入a到达A1状态，从A1状态开始，状态开始分为两路：当输入b时，软件正常运行，到达A2状态，如果输入c，那么软件直接到达Q状态。从A2，A3，到An-1的n-2个状态经过不同的输入，可以出现3个不同的状态转移情况，以An-1为例，当输入为h时，软件正常运行，达到An状态，当输入为g时，软件会达到Q状态，当输入为j时，软件返回到A2状态。An和Q不用经过任何输入，直接到达Exit状态。

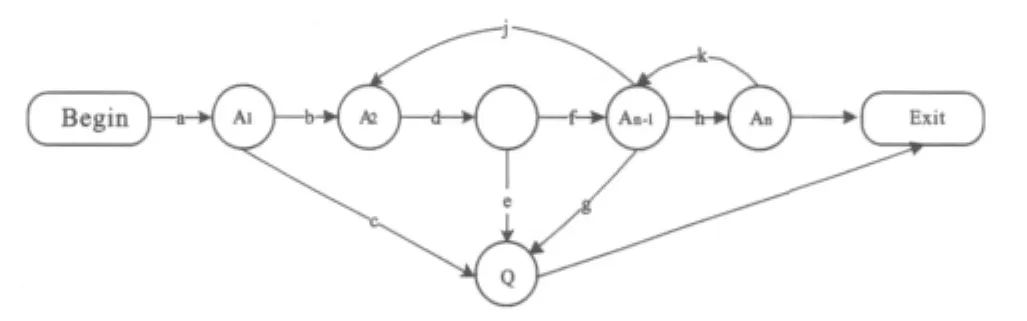
图1 软件状态转移

依据马尔可夫链的无后向性特点，结合软件运行流程的状态转移情况，我们定义软件的异常概率为：

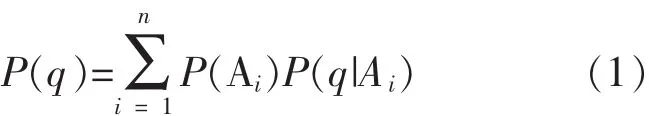
式 （1）中：q——Q所在的状态；

Ai——软件运行过程中的各状态。

通过公式 （1）可以看出，软件异常的概率等于各状态的概率乘以每个状态的异常概率之和。那么软件的可靠性为：

式 （2）中：r——软件的正常状态。

由于公共利益的软件需要可靠性，因此我们定义当P（r）≥99.5%时，则该软件是可靠的。

根据使用模型，可以手动或自动产生测试用例。从Enter状态开始，生成状态和激励的序列，到达Exit状态，然后通过不同的激励生成下一个马尔可夫链，直至满足一定的测试充分性准则，便可停止测试用例的生成。在模型存在循环时，需规定循环次数，避免产生无限长的测试用例。通过充分的测试用例可以统计出关键的数据值：P（q|Ai）和 P （Ax|Ay）， 其中 i， x， y∈T， T={1， 2， 3， …n}。由于马尔可夫的无后向性，可得如下公式：

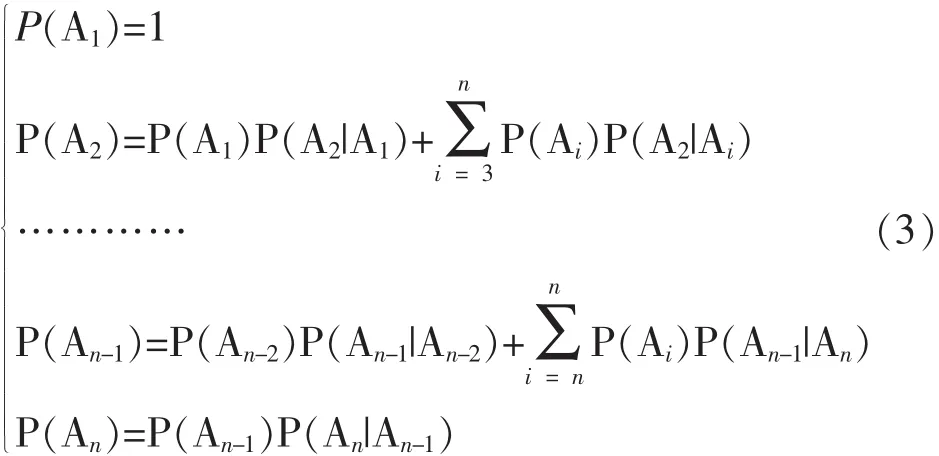
此公式 （3）中含有n个未知数，分别为P（A1）， P （A2）， …， P （An）。 同时由于 P （Ax｜Ay）是可测试统计值，为已知数，其中x，y∈T，T={1，2，3，…n}。则由线性代数可知n个方程，n个未知数，可以解出该线性方程，则得到：

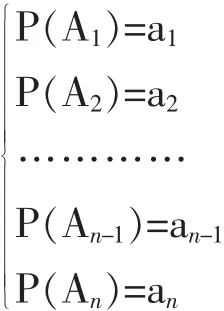
其中，a1，a2，……an为已知数。由于软件异常性概率等于每个过程的状态概率乘以每个过程在此状态下有异常的概率之和。经过上面的分析可知，每个状态的概率为已知数，而每个状态发生异常的概率同样是已知数，那么，软件异常概率则是可计算的。则P（r）同样是可计算的。至此，软件可靠性计算方式可行。

3 实例分析

本节将针对图2所表示的某A软件系统的运行流程，结合本文提出的可靠性评估模型和方法，给出可靠性评估的示例，计算出系统的可靠性并对其结果加以分析，以考察本文所提出方法的正确性和有效性。

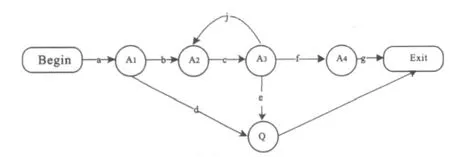
图2 A软件运行流程

A软件的运行流程从Begin开始，经过4个中间状态 （正常），最后到达Exit状态。每一状态转移对应一次输入，即一次激励。由于模型中从A2到达A3状态自后，可能A3状态又返回A2状态，所以通过规定，此种情况时，循环次数不超过2次。利用马尔可夫链模型，每次通过一个测试输入，即得到一种状态流程图，最后达到Exit状态。同时，利用输入大量的测试用例，可以得到大量的统计数据。从该数据中可以统计得出每个状态下通过一种输入之后的异常概率P（q|Ai），其中i={1，2，3，4}和每个状态下下一个状态的概率P（Ax|Ay）， 其中， x，y∈T， T={1，2， 3，4}。

依据马尔可夫链的无后向性特点，结合软件运行流程的状态转移情况，我们定义软件的异常概率为：

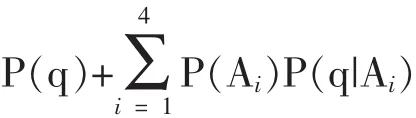
其中，q表示Q所在的状态，Ai表示软件运行过程中的各状态。可以看出，P（q|Ai）是已知的，关键点在于计算 P （Ai）， 其中 i={1， 2， 3， 4}。通过公式 （3）可知：

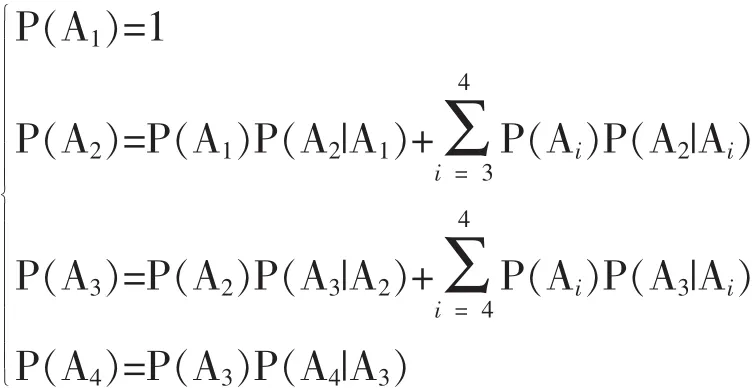
通过之前的分析，假设：P（q|A1）=0.07，P（q|A3） =0.01， P （q|A2） =0， P （q|A4） =0； 同时通过统计测试，假设P（A2|A1）=0.93，P（A3|A2）=1， P （A2|A3） =0.05， P （A4|A3） =0.94， 则将数据代入公式可得：

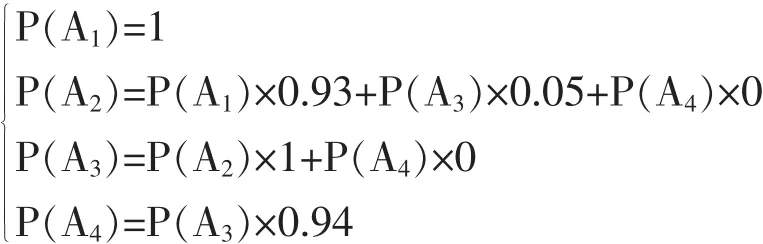
可得： P （A1） =1， P （A2） =P （A3） =0.98， P（A4）=0.92。软件异常的概率等于各状态的概率乘以每个状态的异常概率之和。那么该软件的异常概率为：

则根据公式P（r）=1-P（1）得软件可靠性概率为： （1-0.08）*100%=92%。

当需求定义P（r）≥99.5%时，则该软件是可靠的。依据这个判别方法，可得该软件是不可靠的。

4 结束语

现有软件系统的运行环境逐渐朝着更加开放的方向发展，在这种情况下如何对软件的可靠性进行快速、有效的衡量成为一个急需解决的问题。本文基于马尔可夫链模型研究软件可靠性评估方法，通过建立目标函数模型，分析目标函数的计算方法，给出目标的判别方法，得出基于马尔可夫链的迭代算法来评估软件可靠性是可行的。该方法不但能够充分、准确地得到评估结果，同时还能指导软件可靠性的分析，为以后的系统优化提供更多的参考。在今后的工作中，还需要通过实际项目的应用来进一步检验该方法的有效性和可操作性；同时，利用软件可靠性研究方法进行优化和改进软件是一个可以深入研究的方法。

[1]MUSA J D.Softward reliability engineering[M].New York： McGraw-Hill， 1998： 1-142.

[2]DOWNS T，GARRONE P.Some new methods of software testing with performance comparisons[J].IEEE Trans.Relia， 1991， 40 （3）： 322-337.

[3]WHITTAKER J A，POORE J H，Markov.Analysis of software specification[J].ACM Trans.Software Engineering and Methodology， 1993， 2 （2）： 93-103.

[4]CHEN Huo-wang， WANG Ji， DONG Wei.High confidence software engineering technologies[J].Acta Electronica Sinica， 2003， 31 （12A）： 1933-1938.

[5]SELDING P B.Faulty software caused Ariane 5 failure[J].Space News， 1996， 25 （7）： 24-30.

[6]LEVE SON NG，TURNER CS.An investigation of the Therac-25 accident[J].IEEE Computer， 1993， 26 （7）：18-41.

[7]ZHANG YQ， SUN SJ.Software reliability modeling based on unascertained theory[J] .JournalofSoftware，2006， 17 （8）： 1681-1687.

[8]赵玮，杨莉.软件模块测试中的动态资源分配问题 [J].运筹学学报，2000，4（3）：88-94.

[9]刘云.计算机系统可靠性若干问题研究 [M].西安：西安电子科技大学出版社，1998.

[10]陈丽敏.基于马儿可夫链模型的软件可靠性测试方法研究 [D].成都：电子科技大学，2010：22-25.

[11]DAVID L P， JOHN A， KWAN S P.Evaluation of safetycritical software[J].Communica-tion of ACM，1990，33（6）： 636-648.

[12]PARNAS D L， ASMIS GJ K， MADEY J.Assessment of safety-critical software in nuclear power plants[J].Nuclear Safety， 1991， 32 （2）： 189-198.

[13]HOWDEN W E.Good enough versus high assurance software testing and analysis methods[C]//In:Regina S Sed.Proceedings of the Third IEEE International High Assurance Systems Engineering Symposium.Washington D C：IEEE ComputerSociety， 1998： 166-175.

[15]刘斌，陆民燕，阮镰.基于模糊神经网络的软件可靠性早期预计方法 [J].北京航空航天大学学报，2001，27（2）： 237-240.

[16]吴超，林家骏，俞岭.软件可靠性建模研究 [J].计算机工程，2008，34(11)：52-54.

[17]QIN Zhi-dong， LEI Hang， SANG Nan， et al.Study on the reliability demonstr-ation testing method for safetycritical software[J].Acta Aeronautica et AstronauticaS-inica， 2005， 26 （3）： 334-338.

[18]朱连章，李妍深.用于软件可靠性分析的分解方法 [J].计算机工程与设计，2007，28（24）：5835-5837.

[19]MILLER W M， MORELL L J， NOONAN R E， et al.Estimating the probability of failure when testing reveals no failures [J].IEEE Trans On Software Engineering，1992， 18 （1）： 33-43.