一种基于预测遭遇点的制导控制一体化算法*
2012-12-10乔朋朋李小兵
乔朋朋,李小兵,刘 彬,刘 君
(空军工程大学防空反导学院,陕西三原 713800)
0 引言
导弹制导和控制系统传统的设计方法是忽略它们之间的相互作用,分别单独的处理每个子系统,待每个子系统设计好以后,再将它们组合在一起。尽管这种方法在过去被证明是有效的,但这种方法不能总协调好各系统之间的关系,不利于整个导弹系统性能的提高,这就有必要将制导和控制作为整体一起来进行设计[1]。自 C.F.Lin 最早在文献[2]中提出一体化的思想以来,国内外学者在制导控制一体化领域所开展的研究有很多,如张保群等在文献[3]中提出一种基于自适应滑模控制的导弹制导与控制一体化反演设计,很好的实现了对目标的拦截和对性能指标的跟踪,然而,这种方法只适用于对相对速度不是很大的目标进行拦截,对于于弹目相对速度很大,尤其是迎面拦截的情况,这种方法就不适用了。因此,如何对高速度、大机动的再入大气层目标进行有效拦截是一项重要的研究内容。
文中通过对弹目相对运动及其他环节进行合理的建模,基于预测遭遇点的思想,采用反演和滑模控制思想,设计出能够有效针对再入大气层机动目标的一体化制导控制算法。
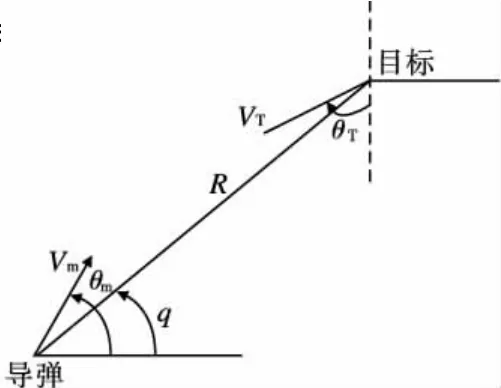
图1 弹目相对运动模型
1 模型建立及分析
1.1 模型建立
1.1.1 弹目相对运动模型
首先,建立弹目相对运动模型,以平面拦截为例,建立弹目相对运动模型如图1所示。
图中:Vm、VT为导弹和目标的速度;R为弹目距离;q为弹目视线角;θm为导弹的弹道倾角,θT为目标的再入角。
由图中可以得到弹目相对运动方程如下:
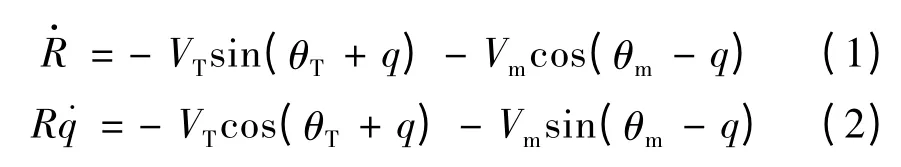
1.1.2 导弹质心运动的动力学方程
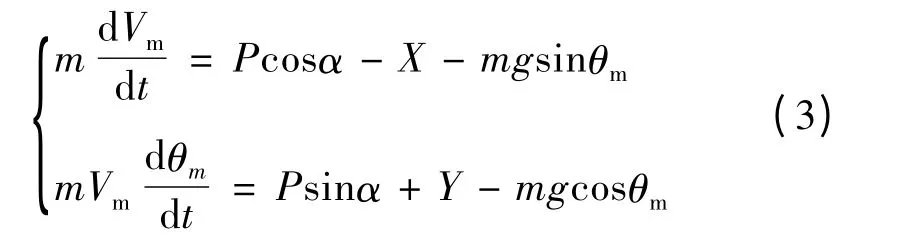
1.1.3 导弹质心运动的运动学方程
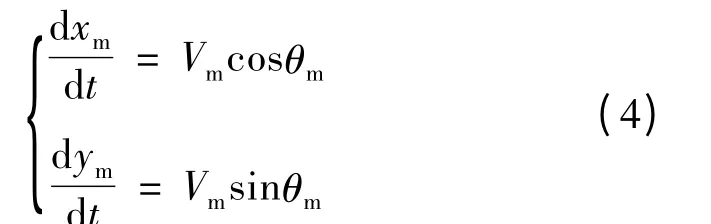
1.1.4 导弹的气动力模型
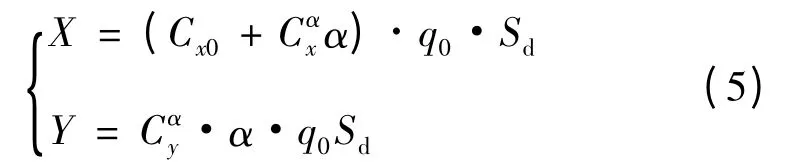
1.1.5 导弹的攻角模型
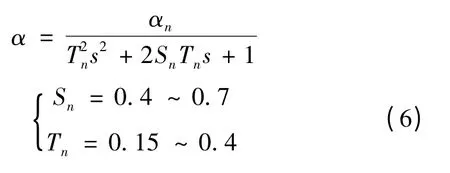
其中:
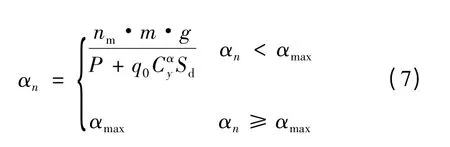
其中,nm为制导指令,不妨令其为u。
1.2 模型分析
由式(6)可以推出:
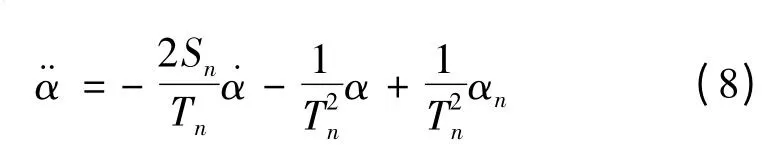
令nm=u,则可以将式(7)化为如下形式:
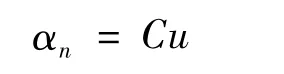
则式(8)可以变为:
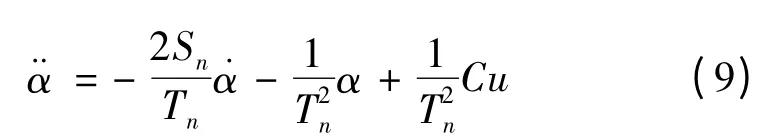
由式(3)可以得到:
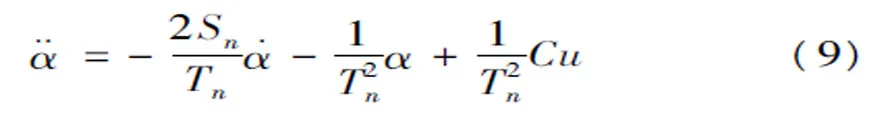
令x1=θm,x2=α,x3=˙α,则由式(9)和式(10)可以得到如下状态方程:
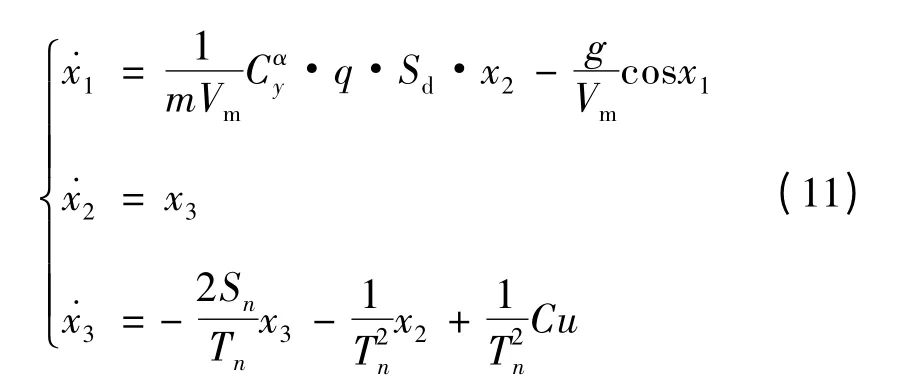
令:
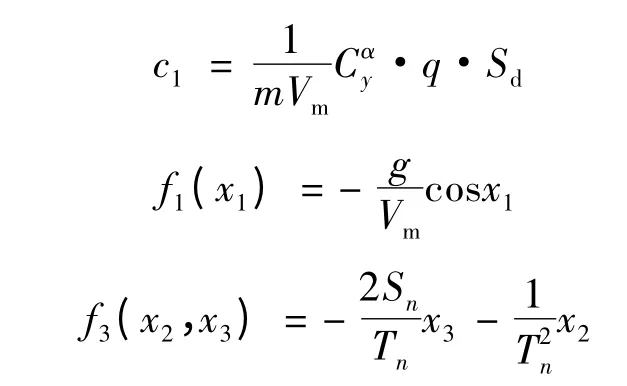
则式(11)可以变为:
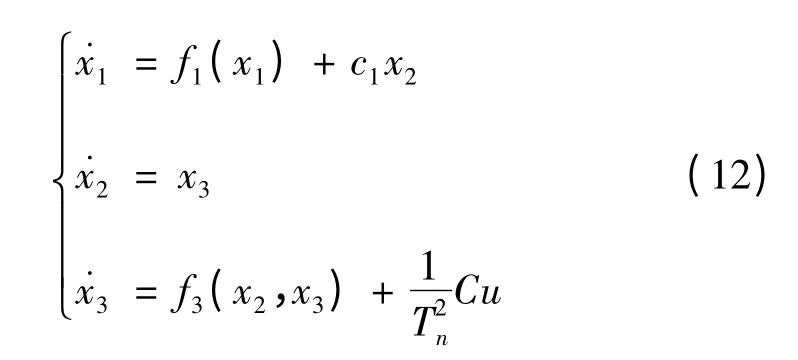
2 一体化制导控制算法推导
2.1 基于预测制导的制导方程[4-6]
预测制导的目的是使拦截弹在攻击机动目标时能够获得尽可能平直的弹道,或者机动到直线上飞行,类似于比例导引制导的拦截弹攻击非机动目标。
以纵向平面为例,在导弹攻击目标的末段,为了使导弹能够以直线击中目标,可以取在每一时刻,弹目能按理想直线飞行时,剩余时间内在垂直于视线上的距离应相等,由此得到:
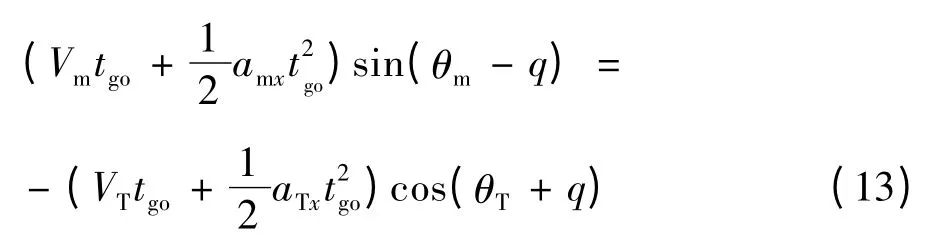
其中:amx、aTx分别为导弹和目标沿着速度方向的加速度。假设目标的机动加速度只改变速度的方向而不改变大小,即=aTx=0,两边同除以 tgo,经化简可以得到:
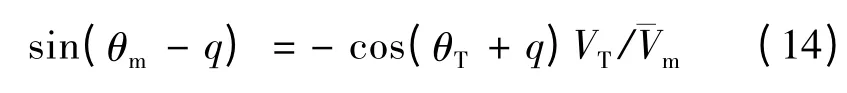
进而可以得到使导弹沿直线飞向目标的理想弹道倾角:
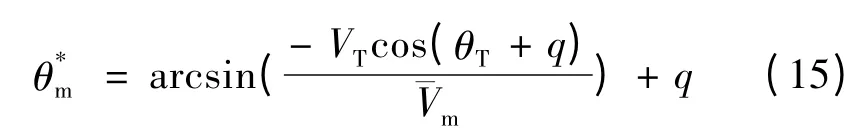
由式(2)可知:
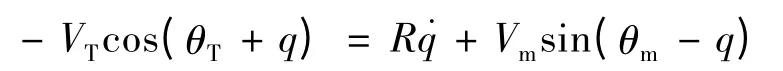
则式(15)可以变为:
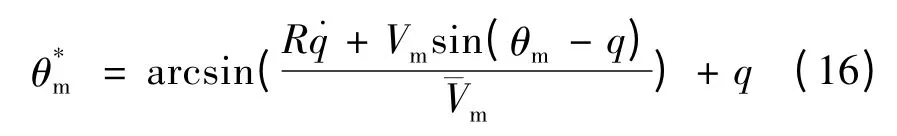
其中,剩余时间tgo可以由下式求得:
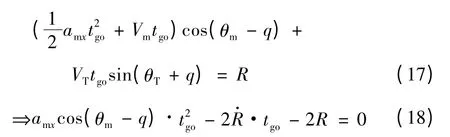
将导弹的实际弹道偏角与理想弹道偏角的偏差定义为飞行误差,如下:

设计制导控制算法的目的就是通过不断修正弹道倾角,使飞行误差e不断趋近于零,最终近似沿直线飞向目标。
2.2 反演控制器设计
为了实现对弹道倾角的不断修正,可以取导弹和目标在每一个微小变化时刻的状态,它们在这各个微小时刻的状态可以近似为线性。这样可以作如下假设:由于在每一个时刻,使导弹沿直线飞向目标的是唯一的,从而可以假设在每一时刻=0。
用文献[7]中的反演控制器设计步骤来进行一体化制导控制算法的推导。具体过程如下:
步骤一:
定义跟踪误差:
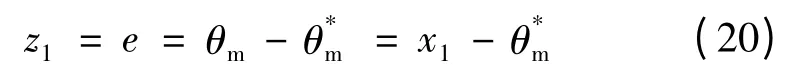
基于上述假设,对式(20)求导可得:
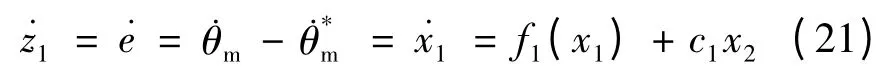
定义虚拟控制量:
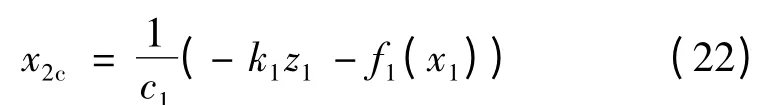
其中,k1> 0。
定义跟踪误差:

定义Lyapunov函数:

则:
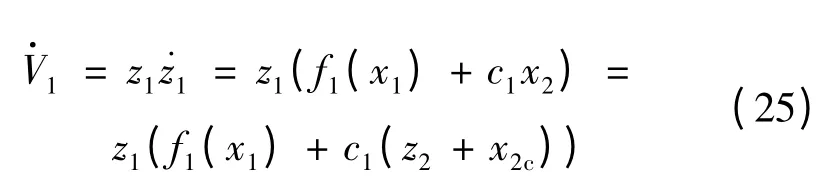
将式(22)代入(25)得:
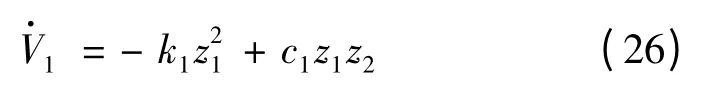
由上式可以看出,只有z2=0时,才能保证恒有≤0,为此,需要进行下一步设计。
步骤二:
对式(23)求导可得:
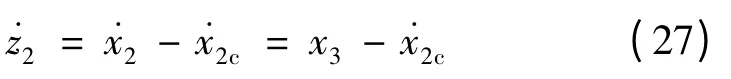
定义虚拟控制量:
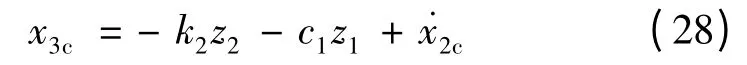
其中,k2> 0。
定义跟踪误差:

定义Lyapunov函数:

则:

将式(27)和式(29)代入式(31)可以得到:
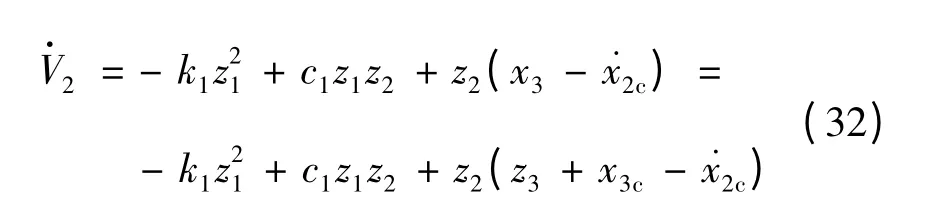
将式(28)代入上式:
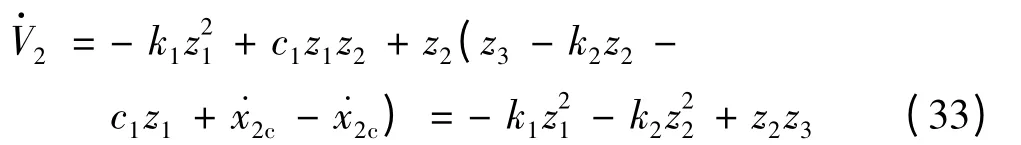
由前一步的分析知,z2不一定为零,这就由式(33)可以看出,只有z3=0时,才能保证恒有V·2≤0,为此,需要进行下一步设计。
步骤三:
定义Lyapunov函数:

对式(34)求导得:

对式(29)求导得:
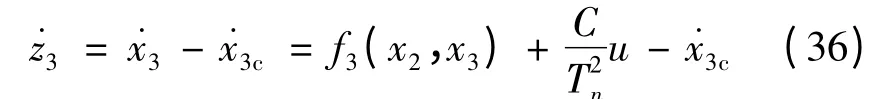
将式(36)代入式(35)可得:
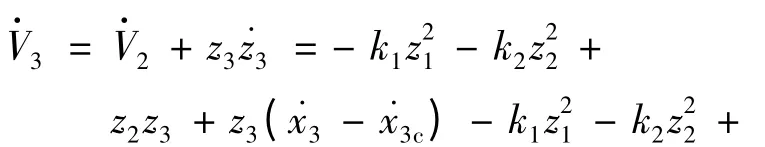
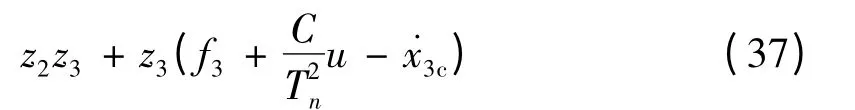
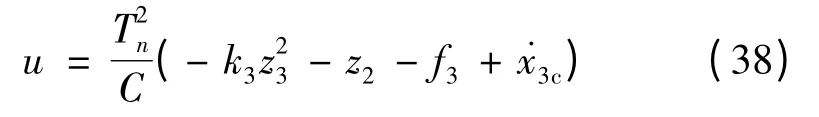
其中k3>0。
将式(38)代入式(37)得:
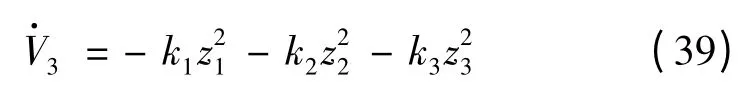
通过控制律的设计,使得系统满足了李亚普诺夫稳定性理论条件,z1、z2和z3均以指数形式渐近稳定,从而保证系统具有全局意义下指数的渐近稳定性。
可见,对于状态方程(12)采用以上所推导出的制导控制算法,可以使各状态达到最终稳定并满足系统的控制要求,即。
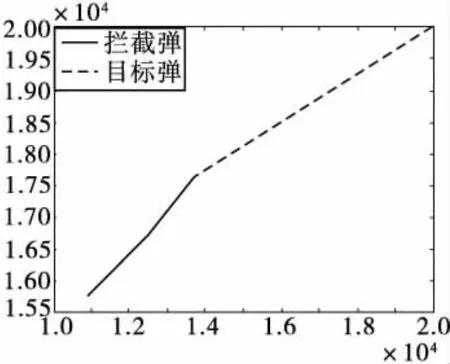
图2 弹目相对运动曲线
3 仿真结论
设置初始值:目标弹速度 2.5km/s,且以最大过载为3g的加速度作正弦形式的机动,目标弹初始再入角取为70°;初始弹目距离为15km,拦截弹初始弹道倾角为30°,初始速度为1.5km/s;初始弹目视线角为30°。具体仿真结果见图2~图4。
从图2可以看出,拦截弹弹道比较平直,较好的对目标弹进行了拦截;从图3中实际变量,即拦截弹弹道倾角的控制效果可以看出,拦截弹的实际弹道倾角在不断的进行调整,逐渐的趋近于使拦截弹近似理想飞行的理想弹道倾角,虽然最终存在一些偏差,但是相对来说已经非常小了,可以将此时的拦截弹近似为沿着直线飞向目标。需要说明的一点是伪变量,即拦截弹理想弹道倾角最终的突变现象,这是由于临近弹目遭遇时,视线角速率引起视线角突变所造成的。
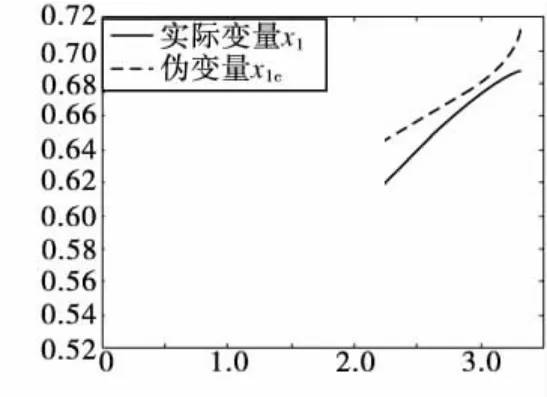
图3 导弹实际弹道倾角跟踪曲线
由图4可以看出,攻角及其变化率都能很好的跟踪其对应的伪指令,同时系统状态没有抖振现象,至于两个伪指令末段的突变则是由于拦截弹理想弹道倾角的突变和三个模态之间的耦合作用所产生的,但是这并不影响最终的拦截效果。
仿真结果很好的验证了所设计的制导控制算法的有效性,为进一步针对模型更加复杂的制导控制算法开展研究有一定的参考价值。
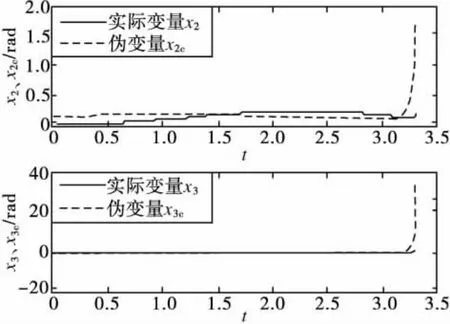
图4 攻角及其变化率与相对应的伪变量的变化曲线
[1]吴鹏.带末端攻击角度约束的制导方法研究[D].哈尔滨:哈尔滨工业大学,2009.
[2]C F Lin,W R Yueh.Optimal controller for homing missiles[J].Journal of Guidance,Control,and Dynamics,1985,8(3):408-411.
[3]张保群,宋申民.基于自适应滑模控制的导弹制导与控制一体化反演设计[J].弹箭与制导学报,2009,29(5):31-35.
[4]吕长起.预测导引律及目标机动的估计[J].航空兵器,1996,3(4):65 -73.
[5]Tal Shima,Oded M Golan.Exo-atmospheric guidance of an accelerating interceptor missile[C]//AIAA Guidance,Navigation and Control Conference and Exhibit,Hawaii,2008.
[6]Manu Sharma,Nathan D Richards.Adaptive,integrated guidance and control for missile interceptors[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit,Rhode Island,2004.
[7]刘金琨.滑模变结构控控制Matlab仿真[M].北京:清华大学出版社,2006:35-50.
