助推滑翔飞行器发射诸元计算方法研究*
2012-12-10陈克俊汤国建
刘 君,陈克俊,谢 愈,汤国建
(国防科学技术大学航天与材料工程学院,长沙 410073)
0 引言
近年来,随着反导技术的提高,传统弹道导弹的生存能力受到严重挑战,由于助推滑翔飞行器飞行轨迹难以预测,容易突防,因此助推滑翔飞行器日益成为各国研究的热点。
发射诸元是指导弹从发射点到目标点的一条飞行轨迹的特征参数。助推滑翔飞行器采用非弹道式飞行轨迹,同弹道导弹相比,飞行轨迹复杂、发射诸元数目众多,且发射诸元方程组为不定方程组,而传统的诸元计算方法如模拟打靶法、区间插值法、参数拟合法等[3~6]无法解决不定方程组问题。因此,助推滑翔飞行器发射诸元的快速计算是一个全新的课题。
文中以助推滑翔飞行器发射诸元计算方法研究为背景,建立了助推滑翔飞行器动力学模型,讨论了助推滑翔飞行器发射诸元的选取及计算难点,通过分析助推滑翔飞行器发射诸元对飞行器飞行轨迹的影响,提出了助推滑翔飞行器发射诸元计算策略,采用牛顿迭代模拟打靶法解决助推滑翔飞行器的诸元快速计算问题。
1 助推滑翔飞行器动力学模型
助推滑翔飞行器由助推火箭和滑翔飞行器两部分构成。助推火箭首先将滑翔飞行器运送到高空,然后与之分离,紧接着滑翔飞行器再入大气层后,由气动力实现变轨进入无动力滑翔飞行阶段。助推滑翔飞行器飞行轨迹可划分为助推段、变轨段和滑翔段,
其中变轨段和滑翔段也可统称为滑翔段。在发射坐标系o-xyz中,助推滑翔飞行器的质心运动数学模型[2]可表示为:
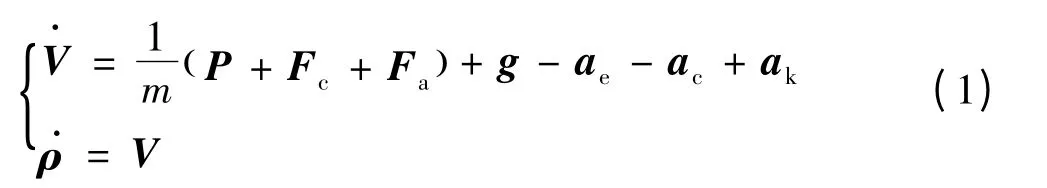
式中:V为飞行器的飞行速度;ρ为飞行器的位置坐标;m为飞行器的质量;P为发动机推力;Fc为控制力;Fa为作用在飞行器上的空气动力;g为地球引力加速度;ae为牵连加速度;ac为哥氏加速度;ak为附加哥氏加速度。各加速度描述为:
牵连加速度:ae=ωe× ωe×( r)
哥氏加速度:ac=2ωe×V
式中:˙m为发动机秒耗量;ωT为飞行器相对于惯性坐标系的转动角速度矢量;ρe为质心到喷管出口中心点距离。
助推段结束后,滑翔飞行器的飞行轨迹及姿态调整均通过气动力作用实现,在此阶段飞行器质心运动数学模型式(1)中发动机推力P和附加哥氏加速度ak均为零。
2 助推滑翔飞行器发射诸元
助推滑翔飞行器飞行轨迹由助推段、变轨段和滑翔段的飞行特征参数共同确定,这些飞行特征参数均是助推滑翔飞行器的发射诸元。
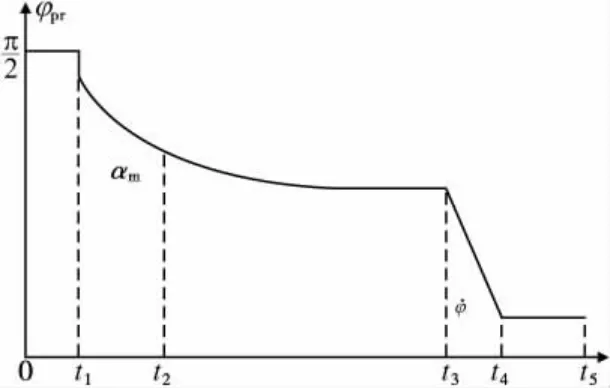
图1 助推滑翔飞行器助推段飞行程序角
2.1 助推段发射诸元
助推滑翔飞行器助推段飞行轨迹与传统弹道导弹主动段相似,可采用相同的飞行程序角模型[2](见图 1):飞行器垂直起飞后不久,飞行器在稠密大气层内实行有攻角转弯,在飞行速度接近跨音速段之前,使攻角收缩为零;飞行速度达到音速后在重力作用下实现转弯;当飞行器飞出稠密大气层后,在飞行轨迹设计时,通过程序角速度˙φ确保飞行器达到预定的再入状态;为提高飞行器的稳定性,在发动机启动、关机以及级间分离前后,要求飞行器保持常值程序角飞行,并尽量减小飞行攻角。据此,飞行程序角模型可取为:其中:t1、t2分别为攻角转弯起始和结束时间;t3、t4分别为程序角速度转弯起始和结束时间;t5为发动机关机时间;αm为最大飞行攻角;Km为攻角参数。对于确定的某型飞行器而言,t1、t2、t3、t4、t5均可以取为常数。同时,由于地球形状不规则以及自转影响,飞行器的飞行轨迹还与发射点经纬度(λ0,φ0)、发射方位角A0有关。因此,助推滑翔飞行器助推段发射诸元包括发射点经纬度(λ0,φ0)、发射方位角 A0、最大飞行攻角αm、程序角速度˙φ以及攻角参数Km。
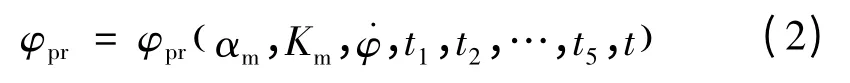
2.2 滑翔段发射诸元
助推段结束后滑翔飞行器的飞行轨迹与弹道导弹被动段完全不同,其飞行轨迹可细分为:变轨段与滑翔段,其每一阶段的飞行轨迹均有其独特的飞行特征参数。
滑翔飞行器变轨段属于无动力飞行,其目的在于在末端获得满足滑翔的初始条件。飞行器的初始滑翔位置并不固定,初始滑翔条件一般是要求高度H、速度倾角满足某特定条件,变轨段飞行器需要充分利用气动力作用进行飞行轨迹调整,因此可将飞行程序攻角αc作为发射诸元。达到初始滑翔条件后飞行器进入无动力滑翔阶段,此阶段诸元与制导方法有关,制导标准参数可视作发射诸元,这里为了简便的说明发射诸元计算的原理,不再增加诸元,制导标准参数视为固定值。当飞行器满足终端条件,计算得到相对落点偏差(ΔL,ΔZ)。变轨段初始滑翔条件高度H和速度倾角约束实际是一个互相制约的条件,这里选取滑翔起点高度H作为约束条件。
综上所述,助推滑翔飞行器发射诸元除了具有与弹道导弹相同的助推段诸元:发射方位角A0、最大程序攻角αm、程序角速度˙φ、攻角参数Km,还增加了滑翔段诸元程序攻角αc等,发射诸元函数方程如式(3)所示:
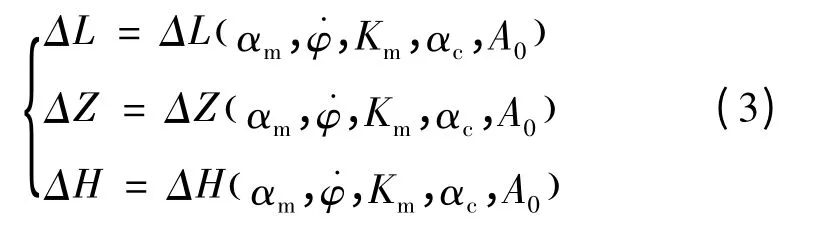
由此可见:1)助推滑翔飞行器发射诸元众多;2)发射诸元函数方程(3)只有3个终端约束条件却有5个未知量,是一个典型的非线性不定方程组,具有无穷多解。这些都为助推滑翔飞行器发射诸元的计算制造了困难。
3 诸元计算策略
按照常规的方法,显然非线性不定方程组(3)很难求解。为了寻求助推滑翔飞行器发射诸元的计算方法,首先分析发射诸元对飞行器飞行轨迹的影响。为了研究方便,文中采用影响因子E来分析发射诸元对弹道的影响,影响因子E定义如下:

其中:∂X/X为自变量的变化比值,∂Y/Y为∂X引起的因变量变化比值。影响因子E的值越大表明自变量对因变量的影响越大。

图2 飞行轨迹示意图
图2 为助推滑翔飞行器飞行轨迹示意图,N为北极,O为地心,飞行器从发射点L起飞,在C点降落。弧线LC对应的地心角β称之为射程角,弧线LC与弧线LN构成的球面角Ad称
之为落点方位角。助推滑翔飞行器的飞行轨迹可以由射程角β、落点方位角Ad、滑翔起点高度H表示。
1)发射方位角对弹道的影响
由表1分析可知,发射方位角对射程角β、落点方位角Ad、滑翔起点高度H均有较大的影响。

表1 发射方位角影响因子
2)飞行程序对弹道的影响
由表2的影响因子分析可知,主动段飞行程序参数最大飞行攻角αm、程序角速度˙φ、攻角参数Km对射程角β和滑翔起点高度H有较大影响,而对落点方位角Ad的影响较小,变轨段飞行程序参数程序攻角αc均对滑翔起点高度H有较大影响,而对其它两个弹道参数影响较小。
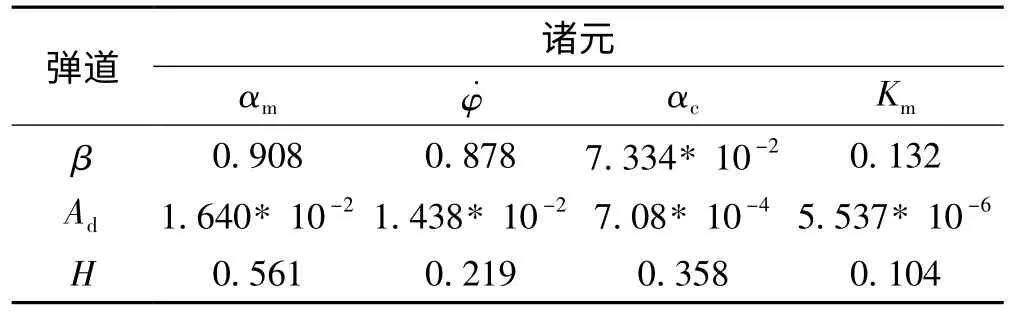
表2 飞行程序影响因子
综上所述,飞行器射程的远近主要是由发射角A0、最大飞行攻角αm、程序角速度˙φ所主导,而飞行器落点的方位角Ad则主要是由发射角A0决定的。因此,根据发射诸元对飞行轨迹的影响大小可将诸元分成两组:一组为发射方位角A0、最大飞行攻角αm、程序角速度˙φ;另一组为发射方位角A0、攻角参数Km以及程序攻角αc。这样发射诸元函数方程组可分解为以下两个恰定方程组:
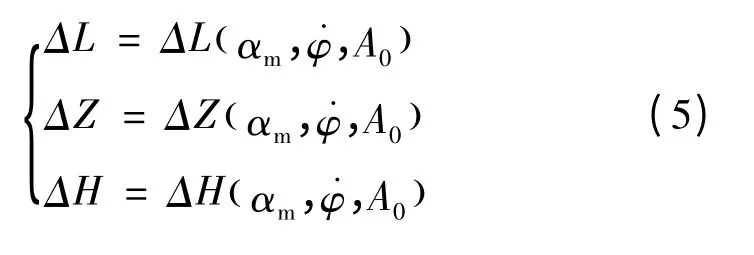

所以助推滑翔飞行器发射诸元的可分为如下两步:第一步,固定参数Km与程序攻角αc,放宽落点与滑翔起点高度精度要求,利用牛顿迭代算法求解方程组(5)解出发射方位角A0粗略值以及最大飞行攻角αm、三级程序角速度˙φ3。第二步,在前步计算的基础上固定最大飞行攻角αm、程序角速度˙φ,利用牛顿迭代算法求解方程组(6)解出最终的发射方位角A0精确值、攻角参数Km和程序攻角αc。
4 算法设计
模拟打靶法基本原理如下:由发射点和目标点位置确定初始积分条件,对于给定发射方位角A、最大飞行攻角αm积分弹道求得落点的位置坐标,与目标点位置坐标比较确定落点计算误差,以此误差修正A、αm,再次积分弹道,求得新落点,经过如此若干次反复计算,当落点计算误差达到要求时,最终可求得给定发射点和目标点的一条弹道。
文中采用牛顿迭代模拟打靶算法解算发射诸元[1]。为表述方便,可用向量Y表示助推滑翔飞行器飞行轨迹参数,向量X表示发射诸元,前文描述的诸元函数关系方程式(5)、(6)可改写为如下通用形式:

将式(7)在初始状态参数X0处线性展开得:

可进一步整理式(8)得到:
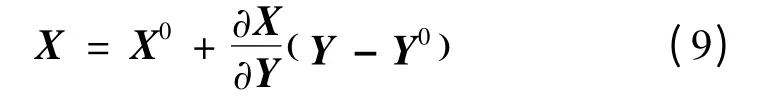

图3 计算流程图
5 算例仿真分析及结论
给定表3中4组初始诸元计算条件,采用文中设计的助推滑翔飞行器诸元计算方法计算得到的发射诸元如表4所示,将这些诸元代入飞行仿真程序,得到飞行器落点及滑翔起点高度偏差如表5所示,图4为表3中4组飞行轨迹图。
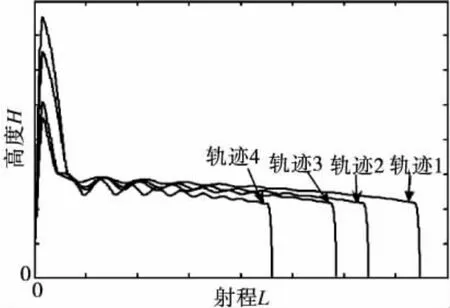
图4 助推滑翔飞行器飞行轨迹
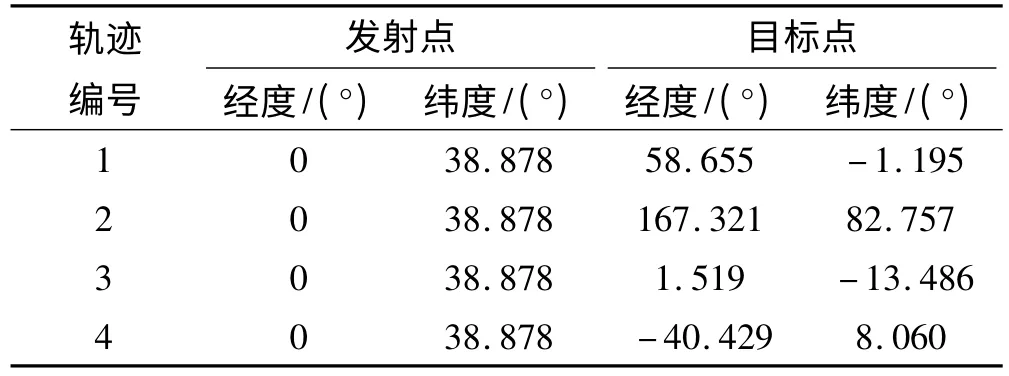
表3 初始条件

表4 诸元计算结果
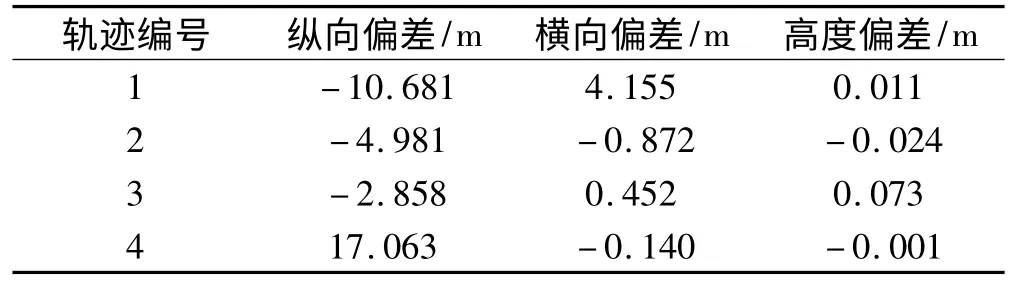
表5 仿真结果
文中基于发射诸元对助推滑翔飞行器飞行轨迹的影响分析,提出了助推滑翔飞行器诸元计算策略,并采用牛顿迭代模拟打靶法设计了诸元计算算法。实际算例中飞行器落点及滑翔起点高度偏差很小,计算迭代次数较少,能很好的满足助推滑翔飞行器快速发射的要求。因此,文中设计的诸元计算方法是可行的。由于文中待解函数没有解析表达式,牛顿迭代诸元计算算法的收敛性有待数学上进一步论证,但现实计算证明是可以收敛的,收敛速度和收敛性与迭代初值的选取有关,其具体情况有待进一步研究。
[1]陈克俊.载入飞船上升段轨道的 Newton迭代设计法[J].国防科技大学学报,1992,14(2):66 -71.
[2]贾沛然,陈克俊,何力.远程火箭弹道学[M].长沙:国防科技大学出版社,1993:217-220.
[3]郝佳新,丁振国,陈克俊.弹道导弹基本诸元的快速装订算法研究[J].计算机仿真,2008,25(4):25 -29.
[4]雍恩米,唐国金.基于摄动制导的弹道导弹发射诸元的仿真算法[J].系统仿真学报,2005,17(5):1048 -1051.
[5]王海丽,陈磊,胡小平.弹道基本诸元的快速装订算法研究[J].国防科技大学学报,1999,21(2):5 -8.
[6]韩东,谷宏强,李洪儒.弹道导弹射程的拟合算法[J].军械工程学院学报,2002,14(3):26 -28.
