我国货币规则的波动性研究

刘振亚，邓 磊

(1.中国人民大学财政金融学院，北京 100872;2.英国伯明翰大学经济学院，伯明翰B152TT)

一、引 言

(一)研究问题和背景

有关货币规则(Monetary Rule)的讨论由来已久，焦点在于不同货币规则在不同历史时期和经济阶段的适用性及其对社会经济变量和福利水平的影响。关于我国货币规则的研究主要集中于数量控制型规则与价格控制型规则的比较。我国现阶段货币规则受到了比较大的挑战和质疑，在利率市场化机制尚不健全的情况下，数量型调控手段受制于国际资本流动、货币流通速度、企业异质性等因素，调控目标与实际效果之间的关联性减弱，货币政策的不确定性问题越来越突出。

一般的结构模型研究大都使用线性近似而并非高阶逼近的非线性近似方法。在线性模型中，货币政策变量通过改变经济变量水平而产生作用。但众所周知，线性近似方法无法捕捉到不确定性本身及其变化对经济变量的真实影响，只能说明随机冲击对变量水平的实际作用。线性近似意味着任何具有相同稳定状态的政策都具有相同的社会福利水平，并且经济主体行为决策过程不受不确定性的影响。这显然与实际情况不符，政策的稳定性关系着预期和效用的形成，经济主体的决策过程也在不同程度上会考虑不确定性因素，并最终带来经济变量的改变。也就是说，政策变量的波动性及其变化会产生真实作用，因此有必要对其波动性变化进行模拟和估计。本文将围绕货币规则问题展开研究，对两种不同的货币规则进行非线性估计，以此为基础对比两者在我国宏观经济下所体现出来的特征和适用性。

(二)文献综述

数量控制型货币规则又称为泰勒规则(Taylor Rule);价格控制型规则又称为麦克勒姆规则(McCallum Rule)。国内关于货币规则类型的研究大致持有以下几种观点。有学者综合使用两种货币规则并进行对比，比如Zhang［1］同时使用两种规则，并认为泰勒规则更为有效;张杰平［2］利用DSGE模型①即动态随机一般均衡模型(Dynamic Stochastic General Equilibrium)。对中国宏观经济中泰勒货币规则和麦克勒姆货币规则政策进行了对比，发现我国更适合采用泰勒规则;冯涛等［3］认为我国货币政策实行的是同时控制货币总量和利率的“双重调控”。Burdekin和Silklos［4］认为中国货币政策更符合麦克勒姆规则;刘斌［5］从社会福利损失角度验证了泰勒规则的优越性;夏斌和廖强［6］从货币流通速度变化、基础货币可控性和货币乘数不稳定性等角度进行分析，认为应该改变数量控制型货币政策中介目标;奚君羊和贺云松［7］利用线性近似方法在DSGE模型框架内分析了前瞻、后顾、同期三种不同预期形成模型下泰勒规则的福利损失比较;谢平和罗雄［8］认为泰勒规则可以很好地衡量中国货币政策。也有观点对泰勒规则提出了质疑，比如徐高［9］认为我国利率市场化并未形成，不宜采用利率调控型货币政策;李春吉和孟晓宏［10］指出，中国货币政策主要依靠信贷调控，利率政策对产出和通货膨胀影响较小，数量控制型货币政策更能代表中国经济实际情况。Huang等［11］的研究表明，普遍采用的前瞻性泰勒规则会增加主要经济变量的不确定性，无论经济是否具有价格粘性、工资粘性、特定资本等特征，这种不确定性在货币规则加入产出因素之后都没有得到改善。

以上研究都是以线性模型为基础，随着国内外研究对非线性结构模型研究的不断推进，货币政策的不确定性得到了更多的关注。Fernandez－Villaverde和Rubio－Ramirez［12］最早将随机波动模型和高阶近似方法引入DSGE模型，利用粒子滤波和随机波动模型分析了宏观经济变量波动性的结构性影响，研究表明非线性模型在经济波动和政策研究中具有显著的解释力，是随机宏观模型所不可或缺的;Justiniano和Primiceri［13］将投资冲击、偏好冲击、技术冲击等因素的随机波动因素加入DSGE模型中，作者发现投资冲击在过去二十年间成为美国经济波动的主要来源;Andreasen［14］针对不同的非线性DSGE模型研究了二阶和三阶扰动近似方法情况下波动性的动态效应，并指出三阶近似在时变波动性研究中的必要性。

本文的重点在于研究时变波动性货币规则的估计问题。在模型设计、求解和估计上，采用非线性的粒子滤波和MCMC(Markov Chain Monte Carlo)方法估计状态空间模型和结构参数，从而从波动性上分析货币规则及其与经济运行之间的密切关系。

二、研究方法与结果

(一)随机波动模型及粒子滤波

随着对上个世纪80年代以来以美国为代表的宏观波动性下降的关注，近些年来国内外宏观经济研究从不同角度和方法力图对宏观经济变量方差的时变性给予解释，包括机制转换方法［15］和随机波动方法［16，17］得到较多使用，前者认为是政策或目标变化带来了方差的下降，而后者认为是客观的随机因素使得变量变化更加平稳。Fernandez－Villaverde和Rubio－Ramirez［12］把随机波动模型引入宏观经济模型，并尝试非线性状态空间模型的非线性模拟解法;Justiniano和Primiceri［13］研究了带随机波动的DSGE模型，该模型对美国经济问题具有很强的解释力。随机波动模型在宏观经济研究领域得到较多的应用，并受到越来越多的重视。

随机波动模型最早应用于金融时间序列研究，用来刻画收益率序列方差随着新增信息的变动情况。一般地，随机波动模型的设计如下:

其中εt，vt～N(0，1)为对均值和波动过程的随机冲击。随机波动模型要解决的问题是如何对非线性、非高斯状态空间模型进行求解和估计。目前，在解决这一问题时通常采用粒子滤波方法(Particle Filter)。粒子滤波突破了卡尔曼滤波(Kalman Filter)在处理非线性、非高斯模型方面之不足，在上世纪90年代得到广泛的发展和应用。自Gordon等［18］之后，粒子滤波方法在理论上取得快速发展［19］，并在实际研究中被广泛应用［20，21］等。

借鉴重要性抽样(IS)的思路，粒子滤波的基本机制如下:

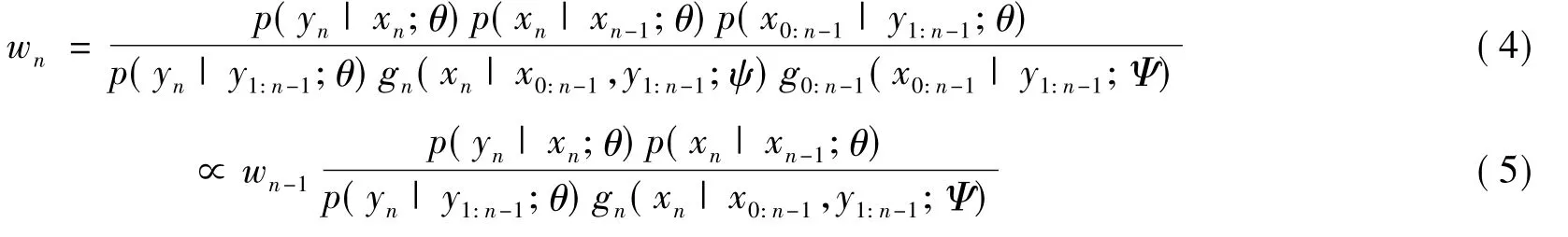
表1 APF算法

(二)随机波动货币规则估计

表2 随机波动模型参数先验分布

随机波动泰勒货币规则设定如下:

随机波动McCallum货币规则设定如下:

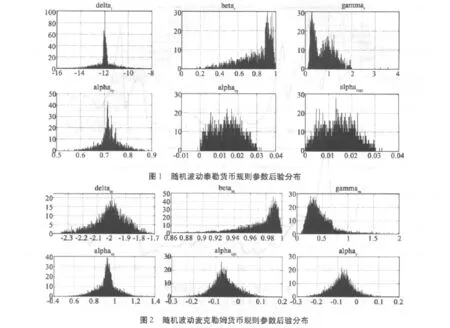
选择1995－2011年相关季度数据①数据来源于中经网数据库。，货币量采用M2指标，利率采用一年期贷款利率。在MCMC方法中对参数的抽样次数M=13000，粒子滤波个数N取5000，前3000次抽样作为废弃样本，得到表3所列参数估计。根据参数估计并利用粒子滤波方法，得到货币规则参数抽样如图1和图2所示:

表3 货币规则参数估计

(三)货币规则波动性估计

在得到货币规则的参数估计之后，经过粒子滤波分别得到关于货币量和利率的货币规则波动性估计，如图3所示。两种货币规则波动性过程均显示出一定的规律性:波动性在1998年和2009年前后达到峰值。而两个时间段分别对应着亚洲金融危机和世界经济危机，也就是说，经济困难时期货币规则的波动性会有突然上升的过程。这种波动性与经济反向变化的关系在已有的研究中也受到了普遍的关注［25］。由波动性随机冲击的持久性来看，两个规则的波动性系数都非常接近单位值，这说明波动冲击具有较强的持久性。另外，在泰勒规则中，波动性总体取值相对较小，而在麦克勒姆规则中，波动性取值较大。这说明数量控制型货币政策在过去近二十年时间里被较为经常地采用以应对物价压力和经济困境，价格控制型货币政策更加遵循规则的规律，只是在经济困难时期被用来平滑经济波动。单纯从波动性的角度出发，泰勒规则相对麦克勒姆规则会暗含较小的波动性，更加具有稳定性。

三、结 论

本文借助随机波动模型和粒子滤波方法研究了泰勒规则和麦克勒姆规则下我国货币规则的波动性问题。粒子滤波对规则中状态变量(波动性)和参数给出了较为准确的估计。从估计结果可以得到以下结论:

首先，由波动性的动态过程可知，波动性的上升和经济困难有着密切的联系。货币政策变量在绝大多数时间里保持着较低的波动性，但经济困难时期往往伴随着波动性的突然增大。这意味着，一般情况下，货币政策变量运动具有自身的规律性;然而当经济向下趋势明显时，货币政策会做出较之以往更为强烈的反应，此时政策的不确定性增加，在对货币政策变量进行预测时需结合考虑宏观经济状况。

其次，从总体上看，泰勒规则的波动性相对较小，从稳定性和可预见性上看，泰勒规则具有一定的优势。泰勒规则伴有较小的波动性，也说明该规则对利率变量的解释力强于麦克勒姆规则对货币量的解释力。该结论为中国宏观经济研究中使用泰勒规则的合理性提供了一定的证据。

最后，虽然目前两种货币规则均显示货币政策变量的波动性已经大体恢复到危机前水平，但仍有一定差距。说明宏观经济中不稳定因素仍未完全排除，世界经济复苏尚待时日，我国经济自身问题仍很突出。为了不断应付经济增长放缓和通胀压力，不排除货币政策变量波动性仍有转而上升的可能性。

本文研究的货币规则波动性问题也可以放在更广泛的视角下来理解，进一步审视该波动性的福利效应和真实效应，从而更准确地捕捉减少波动性和增加政策稳定性的重要价值。本文的研究为一般均衡模型提供了基础，这也是该方向研究需要继续完善之处。

图3 政策变量随机波动方差变化情况说明:上、下图分别为泰勒规则和麦克勒姆规则下平滑后的货币波动冲击(exp(σt))。

［1］ZHANG WENLANG.China’s Monetary Policy:Quantity Versus Price Rules［J］.Journal of Macroeconomics，2009，31(3):473 －484.

［2］张杰平.DSGE模型框架下我国货币政策规则的比较分析［J］.上海经济研究，2012(3):93－102.

［3］冯涛，乔笙，苑为.双重调控下的货币政策绩效研究［J］.金融研究，2006(2):44－51.

［4］BURDEKIN R C K，SIKLOS P L.What Has Driven Chinese Monetary Policy Since 1990?Investigating the People’s Bank’s Policy Rule［R］.East－ West Center Working Paper，2005，No.85.

［5］刘斌.最优货币政策规则的选择及在我国的应用［J］.经济研究，2003(9):3－13.

［6］夏斌，廖强.货币供应量已不宜作为当前我国货币政策的中介目标［J］.经济研究，2001(8):33－43.

［7］奚君羊，贺云松.中国货币政策的福利损失及中介目标的选择——基于新凯恩斯DSGE模型的分析［J］.财经研究，2010(2):89－98.

［8］谢平，罗雄.泰勒规则及其在中国货币政策中的检验［J］.经济研究，2002(3):3－12.

［9］徐高.基于动态随机一般均衡模型的中国经济波动数量分析［D］.北京:北京大学，2008.

［10］李春吉，孟晓宏.中国经济波动——基于新凯恩斯主义垄断竞争模型的分析［J］.经济研究，2006(10):72－82.

［11］HUANG KEVIN X D，MENG QINGLAI，XUE JIANPO.Is Forward－Looking Inflation Targeting Destabilizing?The Role of Policy’s Response to Current Output Under Endogenous Investment［J］.Journal of Economic Dynamics and Control，2009，33(2):409－430.

［12］JESUS FERNANDEZ－VILLAVERDE，JUAN F RUBIO－RAMIREZ.Estimating Macroeconomic Models:A Likelihood Approach［R］.Nber Technical Working Papers，2006，No.0321.

［13］ALEJANDRO JUSTINIANO，GIORGIO E PRIMICERI.The Time－Varying Volatility of Macroeconomic Fluctuations［J］.Ameri-can Economic Review，2008，98(3):604 －41.

［14］MARTIN M ANDREASEN.How Non－Gaussian Shocks Affect Risk Premia in Non－Linear DSGE Models［R］.Creates Research Papers，2010，No.2010 －63.

［15］SIMS C，ZHA T.Were There Regime Switches in Macroeconomic Policy? ［J］.American Economic Review，2006，96:54－81.

［16］PRIMICERI GIORGIO E.Time Varying Structural Vector Autoregressions and Monetary Policy［J］.The Review of Economic Studies，2005，72:821 －52.

［17］CANOVA FABIO，LUCA GAMBETTI.Structural Changes in the U.S.Economy:Bad Luck or Bad Policy? ［M］//Mimeo.Universitat Pompeu Fabra and IGIER，2005.

［18］GORDON N J，SALMOND D J，SMITH A F M.Novel Approach to Nonlinear/Non－Gaussian Bayesian State Estimation［J］.IEEE Proceedings－F，Radar and Signal Processing，1993，140(2):107－113.

［19］DEL MORAL P.Nonlinear Filtering:Interacting Particle Resolution［J］.Markov Processes and Related Fields，1996，2(4):555－580.

［20］CREAL D.A Survey of Sequential Monte Carlo Methods for Economics and Finance［J］.Econometric Reviews，2012，31(3):245－296.

［21］HEDIBERT F LOPES，RUEY S TSAY.Particle Filters and Bayesian Inference in Financial Econometrics［J］.Journal of Forecasting，2011，30(1):168－209.

［22］MICHAEL K PITT，NEIL SHEPHARD.Filtering Via Simulation:Auxiliary Particle Filters［R］.Economics Group，Nuffield College，University of Oxford，1997 － W13.

［23］ARNAUD DOUCET，NANDO DE FREITAS，NEIL GORDON，et al.Sequential Monte Carlo Methods in Practice［M］.Springer，2001.

［24］CHIB SIDDHARTHA，NARDARI FEDERICO，SHEPHARD NEIL.Markov Chain Monte Carlo Methods for Stochastic Volatility Models［J］.Journal of Econometrics，2002，108(2):281 －316.

［25］JESUS FERNANDEZ－VILLAVERDE，PABLO GUERRON－QUINTANA，KEITH KUESTER，et al.Fiscal Volatility Shocks and Economic Activity［R］.PIER Working Paper Archive，2012，No.11:022.