Grassmann流形Gr(2+1，2)上的非线性联络*

何建新

(九江学院理学院 江西九江 332005)

1 预备知识

定义1：n维向量空间in中全体m维线性子空间的集合记作G(m,n),它是m(n-m)维光滑流形，称为Grassmann流形[1].

定义2：主丛P(M,G)上的一个联络,就是对全空间P的每一个x,指定切空间TxP的一个子空间Hx，称为在x点的水平子空间，使满足下列3个条件：

(1)TxP=Vx⊕Hx，这里⊕代表直和；

(2)对每一个元素a∈G,和每一点x∈P,恒存在关系：(Ra)*Hx=Hxa,(a∈G)；

(3)水平子空间Hx光滑地依赖于x[2].

2 主要结果

计算实Grassmann流形空间Gr(2+1,2)上的非线性联络.类似于射影联络的例[3]，设空间上一点的齐次坐标为：

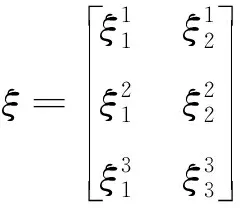
得：

取李群SL(3,i)做结构群，

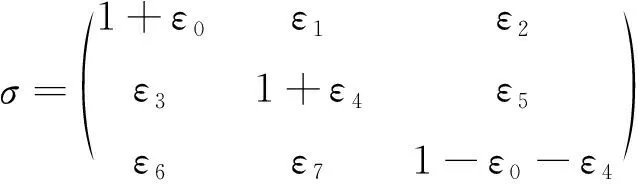
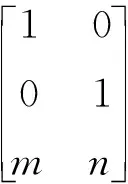
将其转化为流形上的点的局部坐标形式，

(1)

由(1)式可计算得：

(2)

其中：t=(1+ε0+ε2m)(1+ε4+ε5n)-(ε1+ε2n)(ε3+ε5m)

非线性联络可写为：

参考文献：

[1]陈维桓.微分流形初步[M].北京:高等教育出版社,2001.90

[2]黄正中.微分几何导引[M].南京:南京大学出版社,1992.213

[3]陈婧婷.Grassmann流形上的非线性联络[D].北京：首都师范大学,2008.26.